竞争模式下沪宁杭机场旅客吞吐量预测模型研究

曹天捷

（中国民航大学机场学院，天津 300300）

竞争模式下沪宁杭机场旅客吞吐量预测模型研究

曹天捷

（中国民航大学机场学院，天津 300300）

在预测机场旅客吞吐量时需考虑邻近机场间的竞争因素，首先以具有竞争模式的种群动力学理论为基础，通过在种群动力学非线性微分方程组中增加常数项，建立了一般的上海、南京和杭州机场旅客吞吐量耦合的非线性微分方程组，分析该微分方程组的8种具体形式。以预测值和观测值的误差平方和为目标函数，提出了确定微分方程组中系数的优化方法，这种优化方法以逐个多轮次的方式对系数进行优化确定。最后利用所建模型对上海、南京和杭州机场旅客吞吐量进行预测。从预测结果可见，这种预测模型能够较好地反映三地机场间的相互关系和发展趋势。

机场旅客吞吐量；种群动力学；竞争关系；预测模型；优化方法

旅客吞吐量的预测关系到机场的建设和管理，并对机场的定位和发展规划具有重要的意义。目前旅客吞吐量的定量预测方法，如灰色模型预测法[1-2]，人工神经网络预测法[3－5]，支持向量回归预测法[6-7]，逆向重力模型预测法[8]，混合或组合预测法[9-10]等，是根据单一机场的历史数据或机场所在地的经济数据预测机场未来的旅客吞吐量，而未能考虑市场的竞争和导向作用。对于邻近无相互竞争的机场，上述预测方法是合适的，但对于邻近相互有竞争的机场，如京津冀地区和长三角地区的机场，往往出现一场独大的现象。由于无法提供相应的航线（包括国际航线）或者丰富的航班、交通不便，甚至机票价格上不具优势，小机场所在地旅客大量流失[11-12]，其机场旅客吞吐量和当地的人口资源与经济规模等指标极不匹配。因此，在预测机场旅客吞吐量时应将机场与机场之间的竞争因素考虑进去。

本文以具有竞争模式的三变量种群动力学理论为基础，在其动力学微分方程模型中增加了常数项，从而建立了一般形式的上海（含浦东和虹桥机场）、南京禄口和杭州萧山机场旅客吞吐量的非线性微分方程组，利用微分方程组的数值求解方法，并以预测值和观测值的误差平方和为目标函数，提出微分方程组中系数的优化估计方法。运用本文所建立的模型对上海、南京禄口和杭州萧山机场旅客吞吐量进行了预测，预测结果表明这种预测模型能够较好地反映三地机场间的相互关系和发展趋势。

1 模型建立

种群系统Lotka-Volterra（简称LV）模型是描述具有竞争关系的种群生态学模型，目前在工程等领域中有着广泛的应用，如台式计算机和笔记本电脑竞争分析[13]，红色激光和蓝色激光存储方式市场竞争分析[14]，硬盘存储（hard disk drive）和闪存（flash memory）发展竞争分析[15]，高速公路和铁路旅客运输竞争分析[16]，城市道路资源和演化竞争分析[17]。本文将种群系统Lotka-Volterra应用于具有竞争关系的机场旅客吞吐量预测分析。设（ti，x1i，x2i，x3i），i=0，1，2，…，n是某一年ti3个机场的旅客吞吐量观测值，其中x1i代表上海机场旅客吞吐量，x2i代表南京禄口机场旅客吞吐量，x3i代表杭州萧山机场旅客吞吐量。根据实际情况，假设：①上海航空旅客（包括去上海出差或旅游的航空旅客，其他两地的航空旅客含义也是类似）旅行时，不会在其他2个机场所在地换乘交通工具，即在出行时不会先乘其他交通工具到达南京禄口机场或杭州萧山机场，再乘飞机到达目的地，而返回时不会先乘飞机到达南京禄口机场或杭州萧山机场，再乘其他交通工具到达上海；②江苏省航空旅客旅行时，不会在杭州萧山机场换乘交通工具，但可能在上海机场换乘交通工具；③浙江省航空旅客旅行时，不会在南京禄口机场换乘交通工具，但可能在上海机场换乘交通工具；④为简化模型，忽略长三角地区一些小机场对以上3个机场旅客吞吐量变化的影响。长三角地区其他一些机场（如无锡、常州、宁波等机场）旅客吞吐量相比之下比较小[18]，所占份额总计不超过10%（根据2012年的数据，长三角地区其他机场—宁波机场、无锡机场、常州机场、舟山机场和南通机场—旅客吞吐量总计为1 043.391 8万，所占份额为8.53%；而2006年所占份额为7.11%），为简化计算，忽略其影响。根据上述假设并利用三变量种群动力学理论，建立一般形式的机场旅客吞吐量微分方程组为其中：xi，i=1，2，3项表示旅客吞吐量增量和当前的旅客吞吐量有关；考虑到旅客吞吐量往往具有缓慢增长阶段、快速增长阶段和饱和阶段的特点（所谓的S形曲线），增加项描述这样的旅客吞吐量变化特点；x1x2和x1x3项用来描述机场之间对旅客的竞争关系；常数项ai0，i=1，2，3则是为了更好地拟合数据而增加的项。实际运用时，将上述一般形式的机场旅客吞吐量微分方程组分为8种情况：3个常数项都存在、3个常数项都不存在、2个常数项存在而另一个常数项不存在、以及一个常数项存在而另2个常数项不存在。具体用哪种情况下的微分方程组，则是通过比较8种情况下的数据拟合结果，选出一种拟合最好的情况作为最终使用的机场旅客吞吐量微分方程组。

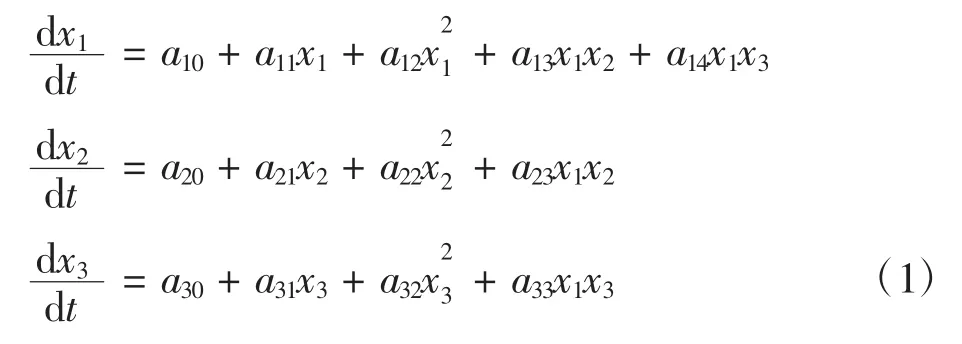
本文主要关注机场旅客吞吐量微分方程组的实际应用，对于这种类型微分方程组的定性理论不进行讨论，有关理论可参见相关文献[19]。

2 模型参数的估计方法

由于微分方程组（1）比较复杂，很难得到解的表达式，因此目前采用近似方法将微分方程先变为代数方程，然后再利用最小二乘法估计系数[20]。这些近似处理方法包括差分代替导数以及用两端点的平均值代替中间点的值。以x1为例，如图1所示，图中ti+1/2=近似处理就是用代替x1（ti+1/2），以及

图1 近似处理示意图Fig.1 Schematic diagram of approximate method

显然，如果两时间点ti和ti+1间距较大，这样的近似处理必然会产生较大误差，从而影响曲线的拟合效果和预测效果。针对这样的问题，本文将t0时的机场旅客吞吐量（x10，x20，x30）视为初始条件，然后针对选定的具体微分方程组形式，对微分方程组进行数值积分得到ti，i=1，2，…，n时刻机场旅客吞吐量的计算值设定目标函数为

从而可以用优化方法确定微分方程组（1）中的各系数。最后通过比较每种微分方程组下的目标函数值，选择一组微分方程作为机场旅客吞吐量的模型。

实际估计系数时，由于不同系数的值相差很大（最大的系数和最小的系数相差若干个量级），以及待优化的系数较多，同时优化所有系数往往很困难。表现出来的现象是：如果优化时的步长和结束优化的判据考虑数值大的系数（步长和数值大的系数量级接近，结束优化的判据比数值大的系数小若干个量级），则会在微分方程组积分时，出现溢出现象；如果优化时的步长和结束优化的判据考虑数值小的系数（步长和数值小的系数量级接近，结束优化的判据比数值小的系数小若干个量级），优化又几乎不起作用。因此本文采用逐个多轮次的方式对系数进行优化确定，即将优化分为若干个轮次，在每一个轮次中，依次对每个系数进行单独的优化确定。这样进行多个轮次的参数优化，直到前后两个轮次计算出的目标函数值相对差异很小（如相对差异小于0.000 1）时，结束优化，从而得到各系数的估计值。这样一种多轮次反复优化的方式虽然比较费时，但因每次只处理一个系数，每次优化时的步长和结束优化的判据可针对不同的系数专门设定。从实际运用结果看，效果比较好。优化方法估计系数的流程图，如图2所示。

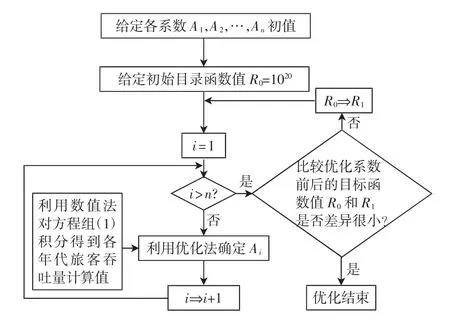
图2 优化估计系数流程图Fig.2 Flow diagram of parameter estimation

图2的各系数是指方程组（1）中系数a10，a11，…，a33的排序，如A1表示a10，A2表示a11等。另外可先将式（1）中的微分方程用近似方法变为代数方程，然后利用最小二乘法得到系数的估计值[20]，并采用这样的估计值作为优化时的初值。本文积分方程组（1）用的方法是变步长龙格-库塔算法[21]，优化估计系数所用的方法为包维尔算法[22]。

3 预测实例

考虑到2003年旅客吞吐量受非典的影响较大，本文只考虑2003年以后的数据。利用2004—2012年各机场的旅客吞吐量统计结果[23]，对于机场旅客吞吐量微分方程组的8种形式逐一分析，可得拟合结果最好的机场旅客吞吐量微分方程组为

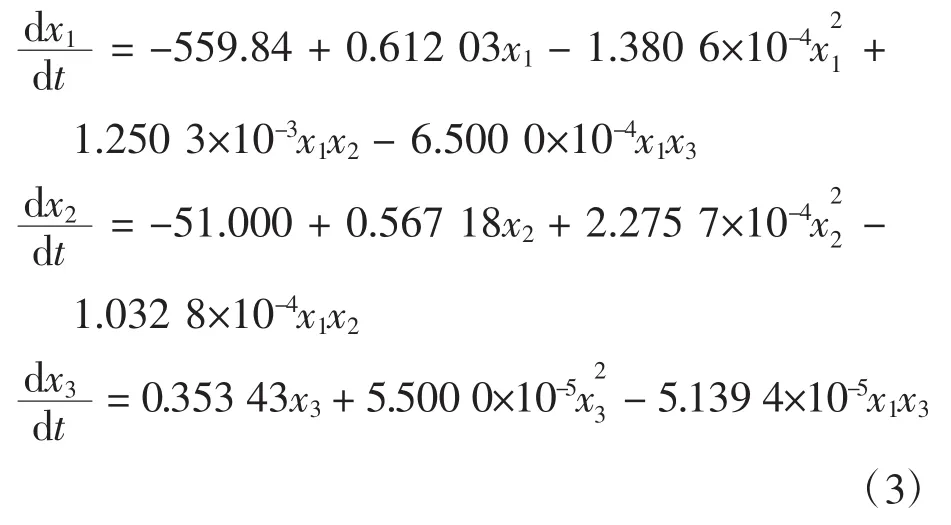
利用数值方法，对方程组（2）积分可得机场旅客吞吐量预测结果（因长三角地区其他机场的旅客吞吐量份额在逐渐增加，长时间不考虑它们的影响是不合理的，因此本文只进行2013—2017年的预测）及误差如表1所示，表1中最大相对误差为6.67%。对方程组（3）数值积分后，可利用式（2）计算出相应的误差平方和为R=5.642 9×105。如果不增加微分方程中的常数项，也不进行优化估计系数，预测结果最大相对误差为15.17%，相应的误差平方和为R=2.262 2×106。由此可见，通过在微分方程中加入常数项和用优化方法估计系数后，最大相对误差下降56.0%，误差平方和下降76.0%，预测结果的精度明显提高。各机场旅客吞吐量所占份额分析如表2所示，表2中最大相对误差为-9.06%。

从预测情况看，在未来的5年内，上海机场仍然占有大部分（2/3左右）的航空旅客吞吐量份额，但旅客吞吐量所占份额有逐渐下降的趋势；南京禄口机场旅客吞吐量所占份额略有增加；上海机场旅客吞吐量所占份额的流失主要被杭州萧山机场占有。由此可见，江苏省的航空旅客流失量仍然非常严重，这可能和京沪高铁、沪宁城际铁路的双线运营，以及江苏经济和旅游发达地区无锡、常州、苏州等地到上海的交通便利有关，而浙江省的航空旅客流失量下降比较显著。

表1 各机场旅客吞吐量预测结果及相对误差Tab.1 Predicting passenger throughputs and relative errors in three airports

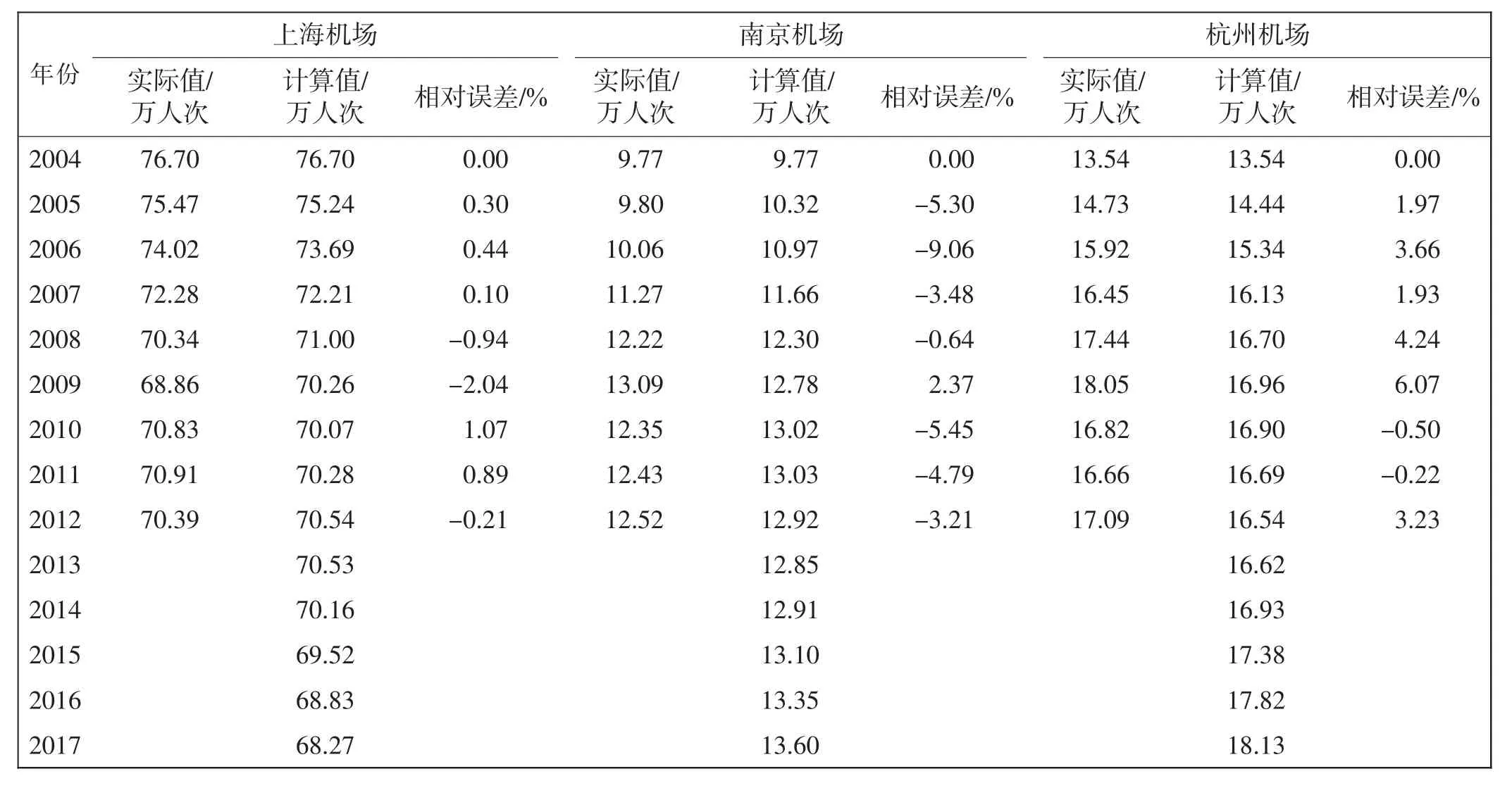
表2 各机场旅客吞吐量所占份额分析Tab.2 Analysis of passenger throughput percentage in three airports

4 结语

本文以种群动力学理论为基础，建立了上海、南京和杭州机场旅客吞吐量耦合的非线性微分方程组，这组方程组中增加了常数项，从而具有更好的适应性。利用微分方程组的数值求解方法，并以预测值和观测值的误差平方和为目标函数，提出了确定微分方程组中系数的逐个多轮次优化方法，避免了同时优化参数时不易确定参数初值的困难。实例中对上海、南京和杭州机场旅客吞吐量进行了预测，从预测结果可见，增加常数项并利用优化方法估计微分方程的系数可以显著提高预测精度，所建立的预测模型能够较好地反映三地机场间的相互关系和发展趋势，预测结果和发展趋势较合理。

[1]陈 东，周圣武.飞机场运量的灰色预测[J].徐州工程学院学报，2005，20（3）：77-80.

[2]姚晏斌，高金华.灰色模型GM（1，2）在机场旅客吞吐量预侧中的应用[J].中国民航飞行学院学报，2006，17（4）：12-16.

[3]吴 璇.基于BP神经网络的航空运输量短期预测模型[J].西安电子科技大学学报（社会科学版），2007，17（3）：67-70.

[4]肖海波，秦鲁敏，阳 劲.基于BP神经网络的机场旅客吞吐量预测[J].山西科技，2005，20（5）：121-122.

[5]廖 成，刘 鲁，晓 斌.机场旅客吞吐量的人工神经网络预测方法[J].小型微型计算机系统，2002，23（12）：1500-1502.

[6]魏 新，冯兴杰.基于支持向量回归的机场旅客吞吐量预测[J].中国民航学院学报，2004，22（3）：45-47.

[7]吴 宁，岳谭谭，邵维亮.首都机场客运量预测[J].科技和产业，2010，10（11）：66-69.

[8]刘晓明，夏洪山.基于逆向重力模型的枢纽机场旅客吞吐量估计方法[J].交通运输工程学报，2008，8（2）：85-89.

[9]葛折贵，葛折圣.基于遗传算法和神经网络理论的机场航空业务量的预测模型[J].现代交通技术，2005，2（4）：65-67.

[10]屈 拓.组合模型在机场旅客吞吐量预测中的应用[J].计算机仿真，2012，29（4）：108-111.

[11]赵桂红.天津滨海国际机场的实际吞吐量预测和机场对策[J].经济地理，2003，23（3）：338-341.

[12]李龙海.天津航空旅客2006年流失预测及流失原因剖析[J].交通运输工程与信息学报，2007，5（2）：24-30.

[13]CHIANG S Y，WONG G G，LI Y，et al.A Dynamic Competition Analysis on the Personal Computer Shipments in Taiwan Using Lotka-Volterra Model[C]//Proceedings of 2008 IEEE Asia-Pacific Services Computing Conference，Yilan：IEEE Press，2008：1413-1417.

[14]PRETORIUS L，PRETORIUS J-H C.A Systems Dynamics Case Study of Competing Optical Storage Technologies under Market Uncertainty [C]//Proceedings of the 2010 IEEE ICMIT，Singapore：IEEE Press，2010：23-27.

[15]TUGRUL U DAIM，PATTRAVADEE PLOYKITIKOON，ELIZABETH KENNEDY，et al.Forecasting the future of data storage：Case of hard disk drive and flash memory[J].Foresight，2008，10（5）：34-49.

[16]WANG YUTING，YAN MENG.The Competition of Highway and RailwayinthePassengerTransportCorridorBasedonSimulinkSimulation[C]// 2011 International Conference on Management and Service Science，Wuhan：IEEE Press，2011：1-4.

[17]YING XIWEN，SHI JING.Road resources distribution and evolution analysis using a species competition model for improving road equity[J]. Tsinghua Science and Technology，2008，13（5）：651-659.

[18]舒严娇.机场旅客吞吐量预测方法研究[D].南京：南京航空航天大学，2008.

[19]林振山.种群动力学[M].北京：科学出版社，2006：67-71.

[20]李兴莉，申虎兰，冯玉广.Logistic和Lotka—Volterra模型参数的灰色估计方法研究[J].大学数学，2004，20（6）：82-87.

[21]徐士良.C常用算法程序集[M].北京：清华大学出版社，1996:177-178.

[22]刘德贵，费景高，于泳江，等.FORTRAN算法汇编[M].北京：国防工业出版社，1983:334-341.

[23]中国民用航空总局规划科技司.从统计看民航2005—2013[M].北京：中国民航出版社.

（责任编辑：刘智勇）

Passenger throughputs forecast model research under competition in airports of Shanghai，Nanjing and Hangzhou

CAO Tian-jie
（Airport Engineering College，CAUC，Tianjin 300300，China）

Taking the competition between nearby airports into consideration during passenger throughput forecast，the general non-linear differential equations with eight different modes about the passenger throughputs in airports of Shanghai，Nanjing and Hangzhou are firstly presented based on the population dynamics theory with competition and addition of constants in classical differential equations.Then an optimization method is presented to estimate the parameters in the equations based on the least square method.In the method the parameters are estimated one by one in some cycles.Lastly the passenger forecast in airports of Shanghai，Nanjing and Hangzhou is performed by using the presented model.It can be seen from the results that the model can reflect the relationships among the three airports and the developments of them.

airport passenger throughputs；population dynamics；competitive relationship；predicting model；optimization method

F562.5；O221.5

：A

：1674－5590（2015）06－0032－05

2014-05-29；

：2014-10-12

曹天捷（1957—），男，山西蒲县人，教授，博士，研究方向为统计理论与方法。