采用信息转换及语言评判的负荷组合预测法

周胜瑜，周任军，李红英，李绍金

（1.智能电网运行与控制湖南省重点实验室（长沙理工大学），长沙 410004；2.长沙理工大学电气及信息工程学院，长沙410004）

当前，组合预测已成为预测中主要的研究方向之一，被广泛应用于各领域，但传统的组合预测方法都是拟合历史数据、获取最小误差的优化预测方法，目标仍然是单一的误差最小，没有计及预测中的不确定性及与专家知识的结合[1-2]。

针对这一问题文献[1-2]提出了基于模糊层次分析法的组合预测模型。文献[3]提出了基于模糊综合评判的组合预测方法。虽然上述两种方法能将专家知识引入组合预测过程中，但二者也面临着一定的问题，主要表现为：第1，专家评价形式的单一化。第2，隶属函数选择主观计算繁琐，在基于模糊评判的组合预测中，模型隶属函数选择的好坏对最终的预测结果有着较大的影响，而隶属函数的选取目前并没有统一的标准。而在基于模糊层次分析法的组合预测中，需要专家对预测模型的不同指标，做两两比较评价，这极大地增加了专家的工作量。第3，专家意见的集成较困难，不同专家之间评价的尺度是不同的，如何消除这种情况的影响，上述两种方法并没有研究。第4，没有有效考虑定量误差指标的影响，在上述两种组合预测过程中对于定量误差的处理，是根据预测效果，由专家直接进行评价或是将两种预测模型的拟合精度直接相比，而这两种方法都比较粗糙，并不能较好地体现定量误差的真实情况。

因此，为解决上述问题，提出一种采用信息转换及专家混合语言评判的电力负荷组合预测法。

1 专家混合语言评判

1.1 评判指标体系的建立

为了更好地评判各种预测模型的性能，必须建立起能反映真实情况的评判体系，这就要求此评判体系应包含定量与定性两方面的指标。

定量指标为历史数据的拟合精度，此项指标与传统的各种负荷预测方法中的数学模型的优化目标一致，其计算式为

式中：xj为拟合精度；T 表示预测的时间跨度表示第j 预测模型在第t 时间的预测值；yjt为实际值。

定性指标包含经济发展的协调性、预测方法的适应性以及决策者对模型的信赖程度3 方面。

预测模型评判体系如图1 所示。

图1 预测模型评判体系Fig.1 Prediction model evaluation system

1.2 语言评判标度

如何通过语言科学、合理地衡量预测模型的性能，对于最终预测结果的产生有着极大的意义，语言评判标度则提供了一个很好的方式，评判中一般采用定量标度如“1、3、5”来表示“弱、中、强”关系。为了更加符合人们的思维情况，文献[4]设定了一种以零为中心对称，且语言术语个数为奇数的加性语言评估标度。

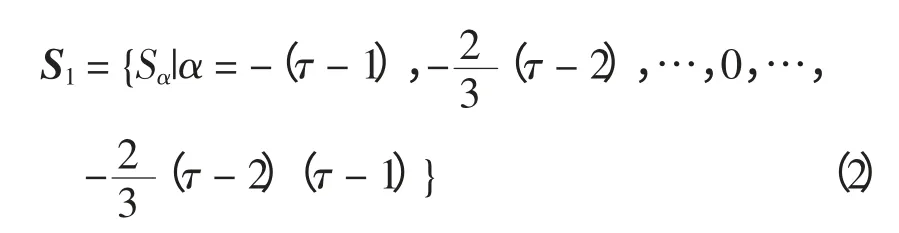
式中：Sα表示语言术语；τ 为标度计算基准。语言术语下标在零右侧的语言术语集为

语言术语下标在零左侧的语言术语集为

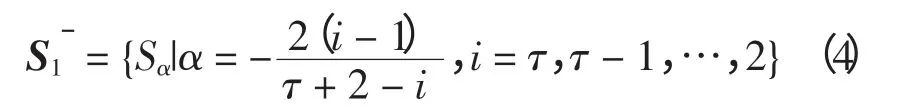
并定义：若α ≥β，则Sα≥Sβ

在信息集成过程中，为避免丢失决策信息，在原有的基础上定义了一个拓展标度。

式中，q（q〉τ）为一充分大的自然数，若Sα∈S1，则称Sα为本原术语；否则，称Sα为拓展术语，不论Sα为何种语言术语皆被统称为确定语言信息。一般地，决策者用本原术语评估指标因素，拓展术语只在计算和评价中出现。语言标度的具体情况如图2所示，若τ=4 则语言评估标度S1中的元素为：S-3=极差；S-4/3=很差；S-1/2=差；S0=一般；S1/2=好；S4/3=很好；S3=极好。

图2 τ=4 时的语言评估标度Fig.2 Lingual assessment scale of τ=4

从图2 中可以看出该类语言评估标度其间距并不均匀，本质上是一种非平衡语言信息，越靠近零点标度越密集，这符合人类的思维情况。

1.3 不确定语言信息

在现实社会中，由于人类语言的模糊性以及问题的复杂性，决策者有时更倾向用类似于“介于“一般”与“好”之间”的表达方式来表达对于某个指标的评价，基于这一情况，定义不确定语言信息如下：

1.4 混合语言信息

在客观条件下，由于决策者知识水平、自信程度以及偏好的不同，往往会导致决策者给出的语言信息是混合的。语言信息的混合性主要体现在以下两个方面。

（1）对于同一决策者而言，其可能选取不同类型的语言信息对预测模型的不同定性指标进行评价，即评价信息可能是确定语言信息也可能是不确定语言信息。

（2）对于不同决策者而言，决策者选取的语言标度可能不同。如决策者A 可能选取τ=4 时的语言标度，而决策者B 可能选取τ=6 时的语言标度。

上述所说的评价语言信息即为混合语言信息。

1.5 混合语言的一致化

第1.4 节中提到决策者在对预测模型进行评价时，所给出的评价值往往是混合的，为了进一步计算模型综合评价值，必须将混合信息一致化。针对语言信息混合情况的不同一致化方法也有所不同。

对于同一决策者，所给语言信息类型不同这一问题，可采用将不确定语言信息转化为确定语言信息的方法。

式中，I 为取下标算子。

则称

为不确定语言信息集成算子，其中γ 的求取方法为

式（10）中数值fφ（[α，β]）计算式为

式中函数φ：[0，1]→[0，1]，具有下列性质：

若x ≥y，则φ（x）≥φ（y），且有

这样可称f 为连续区间信息集成算子，而函数φ（x）则被称为基本单位区间单调函数（basic unit-interval monotonic function），以下简称为BUM 函数[5]。

这种转化方法客观性强，计算方便，非常适合于处理不同类型的语言信息。

针对不同决策者，所选评价标度不同的问题，其一致化方法如下。

设决策者1 所选取的语言评估标度为

其中本原术语个数为2τ1-1。决策者2 所选取的语言评估标度为

其中本原术语个数为2τ2-1，则定义它们之间的转换函数[6]为

通过式（16）～（19）可实现任意两连续性非平衡语言标度的转化。为了保证语言信息的丰富性，规定语言标度的转化一律从低标度向高标度转化，即若τ1〉τ2，则标度τ2向标度τ1转化。

1.6 语言信息的集成

为了更加科学地认识各预测模型的性能以确定模型权重值，必须对专家所给的语言信息进行集成。

如何集成语言信息，是一个十分重要的课题。近年来，许多学者对语言信息的集成方式进行了深入的研究，基于第1.2 节介绍的语言评估标度S1，提出了各种不同的信息集成算子。

文献[7-8]定义了两种语言信息集成算子。分别为有序加权平均算子OWA（ordered weighted averaging）和混合集成算子LHA（linguistic hybrid averaging）。设

式（20）中函数符号OWA 下标变量v 表示加权向量，具体为v =（v1，v2，…，vn），且vi≥0（i =使得

式中：Sβj（j = 1，2，…，n）为语言评价信息（Sα1，Sα2，…，Sαn）中第j 大的语言数据，n 为属性个数。OWA算子的本质是：对数据从大到小按顺序排列，再通过数据所在位置进行集结，权重vi仅反映数据位置的重要程度，与数据本身无关，称为位置权重。以OWA 算子集结语言评价信息可以较好地消除决策者主观评价过高或过低所造成的影响，但是却忽略了属性本身的重要性。为此定义了LHA 算子。设

式（22）中函数符号LHA 下标变量v，w 表示加权向量，具体为v=（v1，v2，…，vn），且vi≥0（i=，使得

式中：Sβj（j = 1，2，…，n）为语言评价信息（nw1Sα1，nw2Sα2，…，nwiSαi，…，nwnSαn）中第j 大的语言加权数据；vi为位置权重，仅反映数据位置的重要程度；w=（w1，w2，…，wn）为语言评价值Sαi（i=1，2，…，n）的权重向量，反映属性本身的重要性与位置无关，可被称为属性权重，wi≥0，且为属性个数，亦称为平衡系数。

LHA 算子既考虑了数据本身的重要性又考虑了数据位置的重要性，可认为是OWA 算子的扩展。

通过利用上述两种信息集成算子可对某预测模型做出一个定量的客观评价。

2 定量指标的转换

2.1 语言标度的模糊化

如前所述，为了更加客观、合理地评价各预测模型，在建立预测模型评价体系时，既考虑了定量指标又考虑了定性指标，而为在统一标准下综合考虑这两类指标且从实际应用角度出发，需将定量数据指标信息转换成定性语言评价信息，因此特将模糊推理技术引入至转换的过程中。

利用模糊推理方法，实现定量数据到定性标度的转化，首先必须将二者模糊化。根据第1.2 节所选取的语言评估标度以及模糊数学的原理定义这些标度在论域X[-q，q]上的模糊集合为A极差、A一般、A极好等，选取目前应用最为广泛的三角函数作为对应模糊集合的隶属度函数，取τ=4 时详细讨论语言标度转换为模糊集合的过程，其转化隶属度函数如图3 所示。图中x 轴表示语言标度值，μ 轴表示语言评价值隶属于对应模糊语言集合的隶属度。

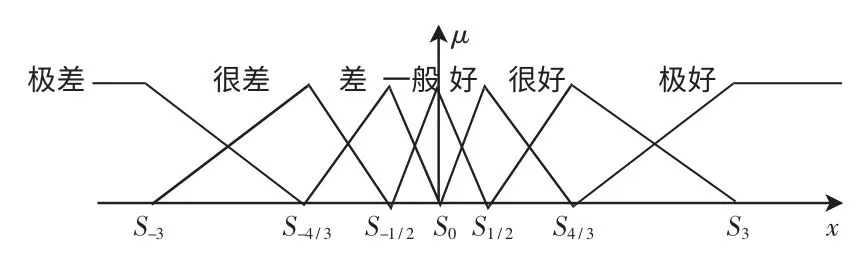
图3 τ=4 时标度隶属度函数Fig.3 Time-scale membership functions of τ=4

2.2 定量数据的模糊化

给定语言标度的模糊集合后，专家还需根据实际情况给出代表相应定量数据的模糊集合。为与语言标度模糊集合相匹配，规定定量数据模糊化后的模糊集合个数应等于语言评价信息模糊化后的模糊集合个数且命相同名称，如B极差、B一般、B极好等，取同类型模糊化隶属函数，同时两者各自对应模糊集合的质心相对距离应成比例，具体表示为

式中：ai表示语言评价信息模糊化后第i 个模糊集合的质心，若某个模糊集合有无穷多个质心取其与0 点最近的质心点；bi表示实际数据模糊化后与ai所对应的模糊集合同名称的模糊集的质心；k 为某一常数。图4 表示τ=4 时预测误差绝对值的模糊化结果。

图4 τ=4 时预测误差绝对值的模糊化结果Fig.4 Obscuretheresultsofpredictionerrorabsolutevalue

2.3 模糊推理

通过第2.1 节和第2.2 节的介绍可知定量数据模糊化后的集合与语言标度模糊化后的集合是一一对应的，因此所建立的模糊推理规则应反映这种关系。规则库的建立过程，具体情况如下。

共有7 条规则，在规则库中FRi表示第i 条模糊规则，Sα为专家语言评价信息，x 为定量数据。

建立模糊规则库后，采用取大-取小整合方式，根据所建立的模糊规则和专家语言评价信息对实际数据进行推理，计算式为

式中：U 表示输入x 后最终的推理结果；r 表示由输入数值x 激活的模糊规则数；Ai与Bi分别表示激活的标度模糊集合与定量数据模糊集合。

模糊推理产生的结果是模糊集合，而评价计算需要的是精确值，因此还需对模糊结果清晰化，采用如今比较常用的面积平分法[9]，清晰化最终模糊集合结果。

经过第2.1～2.3 节的计算过程，即完成了将定量数据转化成语言信息的过程。

3 预测模型评价及组合预测

3.1 模型评价

获得专家对各模型所有指标的语言评价信息后即可进行信息的集成评价。根据语言算子的定义，评价模型的重点在于相关权重的确定，而在模型评价过程中需要确定的相关权重主要有两类，分别是专家位置权重和属性位置权重（统称为位置权重）、影响因素权重（也可称为属性权重）。不同类别的权重，其确定的方式是不同的。

对于专家位置权重（或属性位置权重），可依据各专家（或属性）所给评价值的大小顺序进行赋权，即对专家（或属性）的评价值从大到小按顺序排列，再通过评价值所在位置赋予各专家（或属性）位置权重。权重的分布应该是中间高两边低，呈对称形状，以消除专家主观判断的不良影响。确定方法如下。

设φ（x）为BUM 函数，则有

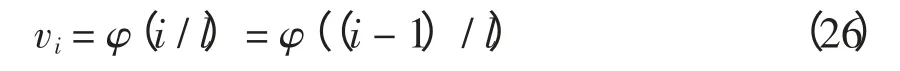
式中，vi为第i 个位置上的专家（或属性）的权重，i =1，2，…，l，l 为专家（或属性）个数，而φ（x）的确定式为

式中，g（y）为聚中函数[10]，满足如下性质：

（1）y∈[0，1]；

（2）g（y）关于0.5 对称；

（3）g（y）为单峰，且在y=0.5 时最大。

利用BUM 函数求得的权重值，满足权重的基本性质，即非负性、和值为1 性。

在实际计算中，依照式（26）～式（27），可令聚中函数

式中，y∈[0，1]，求得位置权重的计算式为

式中，i=1，2，…，l，l 为位置个数，亦可以代表专家个数或属性个数。

对于影响因素权重即属性权重，可采用离差最大化思想，求得属性的权值。该思想的核心是，模型某影响因素评价值偏差越大，则该因素对模型的整体评价影响也就越大，应赋予较大的权重值。其计算过程如下：

设A=（aij）n×m为一致化后的评价矩阵，n 为模型个数，m 为指标个数，则第j 指标的权重为

因影响因素评价值是以语言形式给出的，所以不需要归一化处理。

通过式（29）和式（30）求得各类别的权重值之后，利用OWA 算子、LHA 算子对语言信息做出最终集成得出各模型的综合评分值，其评价步骤如下。

步骤1 利用LHA 算子，单独计算出各专家对各模型的语言综合评价值。

步骤2 利用OWA 算子，综合集成各专家的语言综合评价值。

3.2 组合预测

组合预测模型可表示为

设W=（W1，W2，…，Wn）为专家对n 个预测模型的最终综合评价值，其中，若有模型的评判值小于或等于0，则不考虑该模型的影响，即模型权值为0，如此各预测模型在组合预测中所对应的权重为

式中，r 表示除掉评判值小于或等于0 的模型后剩余模型的个数。

综上所述，基于专家语言评判的组合预测方法主要步骤如下。

步骤1 选取适当预测模型，计算各模型的预测效果（即求取历史拟合精度），并将其作为定量指标信息。

步骤2 邀请专家语言评价各预测模型的定性指标，并将步骤1 中的定量数据转化为定性语言信息。

步骤3 计算相关权重，利用LHA 算子单独计算出各专家对各模型的语言综合评价值，利用OWA 算子综合集成各专家的语言综合评价值。

步骤4 利用W 选取适当预测模型并通过式（32）计算其权重，式（31）进行组合预测。

4 算例分析

以某地区8 年内的负荷预测为例，检验所提方法的可行性。

1）单个预测模型计算

该地区年最大负荷的历史数据见表1。

表1 某地区最大负荷历史数据Tab.1 Acertainregion'slargestloadhistoricaldata

分别选取了二次指数平滑法、三次指数平滑法、灰色预测法、一元线性回归法、非线性回归法、单耗法以及弹性系数法共7 种方法对历史数据进行预测。预测效果见表2。

表2 单个模型预测效果Tab.2 A single model prediction effect

2）定性指标评价

现选取3 位专家分别对7 种预测模型的3 个定性指标进行评价。已知专家1、2 采用τ1，2=4 时的语言评估标度，专家3 采用τ3=3 时的语言评估标度。现以专家3 为例详细介绍模型评价过程，专家3 定性指标语言评价结果如表3 所示。

表3 专家3 定性指标评价结果Tab.3 Expert 3′s qualitative index evaluation results

3）评价信息一致化

取φ（x）=x 并利用式（11）～（19）一致化专家3的评价值。一致化结果如表4 所示。

表4 专家3 一致化结果Tab.4 Expert 3’s consistent evaluation results

4）定量指标信息转换

利用第3 节介绍的信息转换方法，将表2 所示定量数据转换为定性信息，结果如表5 中指标4列所示。

表5 专家3 定性定量指标评价结果Tab.5 Expert 3’s qualitative and quantitative evaluation results

5）专家信息集成评价

得到专家3 定性定量指标评价结果后，利用式（29）和式（30）分别获得属性位置权重以及属性权重为v=（0.146 4，0.353 6，0.353 6，0.146 4），w=（0.405 7，0.142 0，0.324 5，0.127 8），由此利用LHA算子计算出专家3 对各预测模型的综合评价值，如表6 所示。

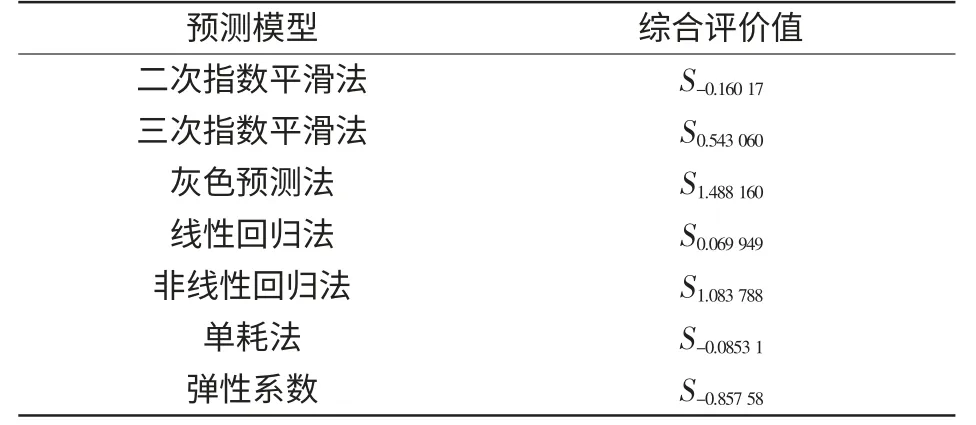
表6 专家3 综合评价值Tab.6 Experts 3’s comprehensive evaluation value

同专家3 评价步骤，分别求出专家1、2 对各预测模型的综合评价值，并再次利用式（29）获得专家位置权重v′ =（0.25，0.5，0.25），进而由OWA算子同各专家评价值，计算出各预测模型的最终评价结果，如表7 所示。

表7 各预测模型最终评价结果Tab.7 Final results of each prediction model

6）组合预测

从各预测模型的最终评价值中，可以看出二次指数平滑法、单耗法以及弹性系数法评价值为负，在组合预测中不以考虑，因此最终的组合预测模型为三次指数平滑法、灰色预测法、线性回归法和非线性回归法，组合中各自所占权重为w*=[0.25，0.40，0.35，0.315]。由此权重向量及各预测模型所求得的组合结果的平均相对误差的绝对值为1.65%，可见以此种方法所得的组合预测结果要明显优于由其它单个预测模型所求得的结果。

5 结论

所提基于信息转换及专家混合语言评判的负荷组合预测法，相比于传统基于模糊评判的负荷组合预测法，有以下4 点优势。

（1）扩展了专家的评价形式允许专家给出不同类型的评价结果，丰富了信息来源。

（2）由专家直接给出语言评价，非常方便，更加符合工程应用的需要。

（3）能够很好地集成各专家意见，有利于预测模型的选取。

（4）建立了定量数据与定性标度之间的转换关系，使之对定量数据的评价更为客观、合理。

需要说明的是，在电力系统中，相较于负荷的短期预测，组合预测方法更适用于中长期负荷预测中。且对于决策者而言，其也可以根据模型最终评价值的好坏选择适当的单一模型进行预测。

[1]吴丹，程浩忠，奚珣，等（Wu Dan，Cheng Haozhong，Xi Xun，et al）.基于模糊层次分析法的年最大电力负荷预测（Annual peak power load forecasting based on fuzzy AHP）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（1）：55-58，67.

[2]丁巧林，潘学华，杨薛明（Ding Qiaolin，Pan Xuehua，Yang Xueming）.最优组合预测方法在电力负荷预测中的应用（Optimal combined forecasting method used in power load forecasting）[J]. 电 网 技 术（Power System Technology），2008，32（S1）：127-130.

[3]孙海斌，周淑雄，谢敬东，等（Sun Haibin，Zhou Shuxiong，Xie Jingdong，et al）.模糊综合评价在负荷最优组合预测中的应用（Application of fuzzy comprehensive evaluation for optimizing combined load forecasting）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2001，13（4）：8-11.

[4]戴跃强，徐泽水，李琰，等（Dai Yueqiang，Xu Zeshui，Li Yan，et al）.语言信息评估新标度及其应用（New evaluation scale of linguistic information and its application）[J].中国管理科学（Chinese Journal of Management Science），2008，16（2）：145-149.

[5]张洪美，徐泽水（Zhang Hongmei，Xu Zeshui）.基于不确定语言信息的C-OWA 和C-OWG 算子及其应用（Uncertain linguistic information based C-OWA and C-OWG operators and their applications）[J]. 解放军理工大学学报（Journal of PLA University of Science and Technology），2005，6（6）：604-608.

[6]徐泽水（Xu Zeshui）.基于语言标度中术语指标的多属性群决策法（A multi-attribute group decision making method based on term indices in linguistic evaluation scales）[J].系统工程学报（Journal of Systems Engineering），2005，20（1）：84-88.

[7]Yager R R.On ordered weighted averaging aggregation operators in multi-criteria decision making[J].IEEE Trans on Systems，Man and Cybernetics，1988，18（1）：183-190.

[8]Xu Zeshui. A note on linguistic hybrid arithmetic averaging operator in multiple attribute group decision making with linguistic information[J]. Group Decision and Negotiation，2006，15（6）：593-604.

[9]石辛民，郝整清.模糊控制及其MATLAB 仿真[M].北京：清华大学出版社；北京交通大学出版社，2008.

[10]Yager R R.Centered OWA operators[J].Soft Computing，2007，11（7）：631-639.