交会测量中方向余弦法的优化方法

王 颖,李佩军,陈佐龙

(中国白城兵器试验中心,吉林白城 137000)



交会测量中方向余弦法的优化方法

王 颖,李佩军,陈佐龙

(中国白城兵器试验中心,吉林白城 137000)

经纬仪交会测量时,常用方向余弦法计算目标坐标。因测角误差,各经纬仪指向目标的射线不相交,计算时有原理性误差。通过分析射线与目标的位置关系及光测设备的测量精度等,提出了用两条射线最短距离的加权值作为目标位置,优化了方向余弦法的计算模型。实测数据验证表明,优化后的方法提高了计算精度,是行之有效的。

经纬仪;方向余弦法;交会

0 引言

光测经纬仪是高精度测量目标轨迹的设备,根据交会测量角,有时需用方向余弦法计算目标坐标[1]。由于测量误差,交会测量的光测设备指向目标的射线不在同一平面内,现用的三角形方向余弦法有原理性误差。通过分析指向目标的两条射线与目标的空间位置关系,提出了用两条射线最小间距的中点作为目标位置,提高了计算精度。应用误差理论,估算了优化算法的误差,证明该方法是有效的。

1 方向余弦法

方向余弦法是用两个测站和目标构成三角形,根据正弦定理和方向矢量计算目标的空间坐标[2]。测站O1、测站O2与目标M的关系如图1所示。

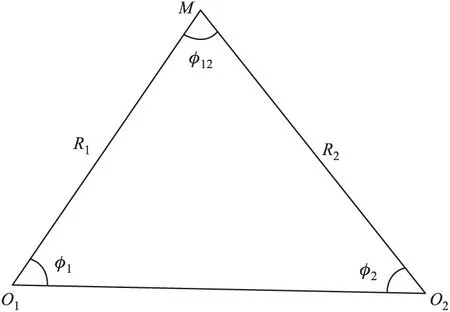
图1 方向余弦法目标位置图

设测站O1距离目标的距离为R1,测站O2距离目标的距离为R2,测站O1方位角和俯仰角分别为A1、E1,射线O1M1方向矢量为:

(l1,m1,n1)=(cosE1cosA1,sinE1,cosE1sinA1)

(1)

测站O2方位角和俯仰角分别为A2、E2,射线O2M2方向矢量为:

(l2,m2,n2)=(cosE2cosA2,sinE2,cosE2sinA2)

(2)

则得目标M坐标可记为:

(3)

式中:cosφ1=[l1(x1-x2)+m1(y1-y2)+n1(z1-z2)]/D12;cosφ2=[l2(x1-x2)+m2(y1-y2)+n2(z1-z2)]/D12;cosφ12=l1l2+m1m2+n1n2;

2 方向余弦法的优化算法

因测量误差,两个测站指向目标的射线不相交,是两条异面直线,如图2所示。采用方向余弦法计算目标坐标存在原理性误差,为解决这个问题,对方向余弦法进行优化,推导出带测量误差的方向余弦法。

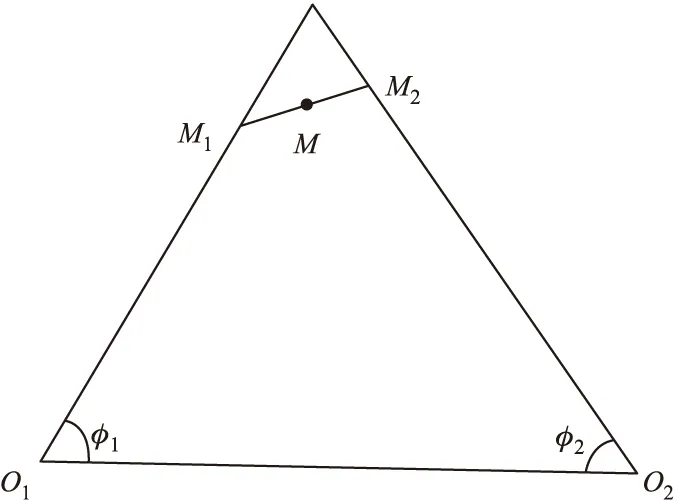
图2 带测量误差的目标位置图

具体推导过程[3]如下:

测站O1坐标为(x1,y1,z1),射线O1M1方向矢量如式(1),则射线方程为:

(4)

令式(4)等于k1,则M1点的坐标为:

测站O2坐标为(x2,y2,z2),射线O2M2方向矢量如式(2),则射线方程为:

(5)

令式(5)等于k2,则射线上M2点的坐标为:

由图2,结合M1、M2点的坐标,可得到垂直于O1M1和O2M2的线段M1M2的方向矢量,即:

M1M2=(x1-x2+k1l1-k1-k2l2,y1-y2+k1m1-k2m2,z1-z2+k1n1-k2n2)

因射线O1M1垂直于M1M2,O2M2垂直于M2M2,有:

O1M1·M1M2=0,O2M2·M1M2=0

则可建立如下方程组:

(6)

解方程组(6)得:

式中,cosφ1、cosφ2、cosφ12、D12见式(3)。

由此可计算M1和M2的坐标分别为:,

那么,M作为M1M2上的点可表示为:

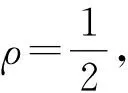
3 精度分析

由交会计算可知,目标坐标x、y、z分别是Ai、Ei、xi、yi、zi(i=1,2)的函数,亦即:

(7)

由式(7)可知,误差有两部分,一是测角误差;二是大地测量基站坐标误差。大地测量精度足够高时,对目标坐标x、y、z的影响可忽略不计。

为了定量分析优化前后的方向余弦法的精度,根据误差传播定律推导出它们的精度公式。由于光学测量系统互不相关,即A1、E1、A2、E2的误差相互独立,设交会的测量系统测角误差相等,即:

σA1=σE1=σA2=σE2=δ

由误差传播定律[4],当Ai、Ei具有均方根误差σAi、σEi,点位坐标xi、yi、zi具有均方根误差σxi、σyi、σzi时,传递给空间坐标z、y、z的均方根误差[5]为:

由于篇幅关系,两个方法的精度公式不在这里详述。为了说明方向余弦法优化前后的精度,我们采用几组真实数据为真值,利用Visual C++语言将两种方法的精度公式编成软件进行计算,比对结果如图3～图6。从比对结果上可以看出,优化后的方向余弦法减小了计算误差。

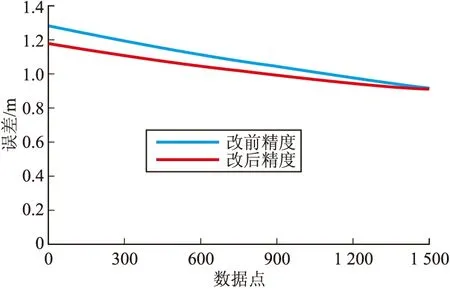
图3 X方向精度比对示意图

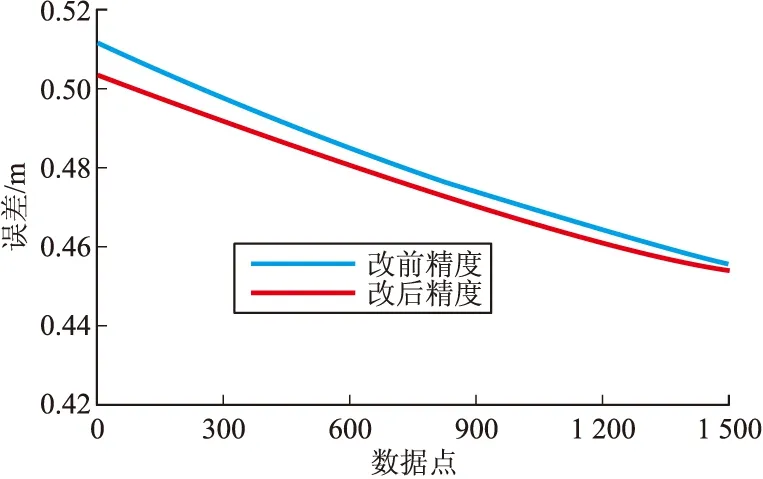
图4 Y方向精度比对示意图

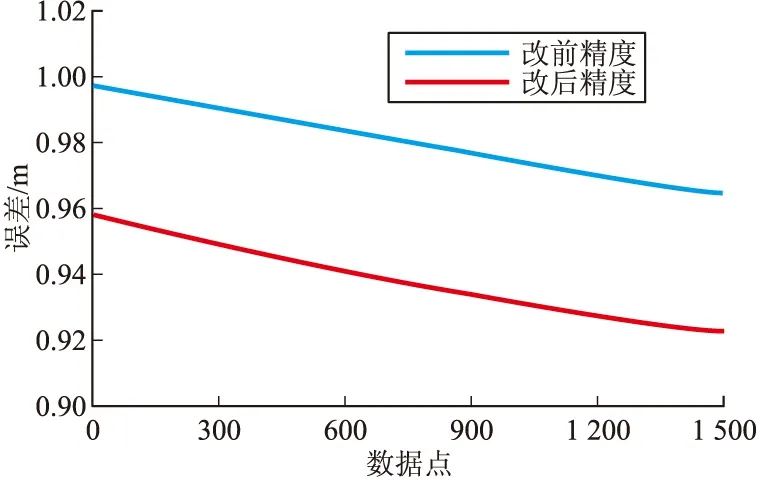
图5 Z方向精度比对示意图

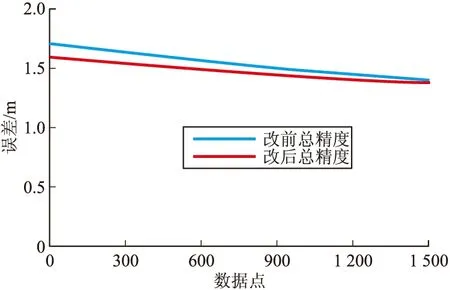
图6 总精度比对示意图

4 结束语

因大气折射及地球曲率误差,光学测量系统会产生测量误差,两个测站指向目标的射线不相交。根据实际情况优化了方向余弦算法的模型,建立了交会测量方法。为了验证优化后的方向余弦法精度,进行了误差分析,推导出精度公式,并利用一组真实数据进行验证。验证结果表明,优化后的方向余弦法更符合实际测量的情况。

[1] 项树林. 基于动态加权的光电经纬仪交会方法 [J]. 光学与光电技术, 2008, 6(6): 51-54.

[2] 孟道骥. 高等代数和解析几何 [M]. 北京: 科学出版社, 2010.

[3] 刘利生. 外弹道测量数据处理 [M]. 北京: 国防工业出版社, 2002.

[4] 费业泰. 误差理论与数据处理 [M]. 北京: 机械工业出版社, 2004.

[5] 王颖, 陈佐龙, 汪向阳, 等. 光雷一体化测量系统的布站优化研究 [J]. 科学技术与工程, 2012, 12(5): 1111-1114.

Optimization Design of Direction Cosine Algorithm Applied in Intersection Measurement

WANG Ying,LI Peijun,CHEN Zuolong

(Baicheng Ordnance Test Center of China, Jilin Baicheng 137000, China)

In view of intersection measurement, direction cosine algorithm is often adopted to calculate coordinates. In fact, because of error of optical equipment, two light rays from them don’t intersect at one point; the direction cosine method is inaccurate in principle. In this paper, through analysis of spatial relationship among rays, target, and measuring accuracy of optical measurement equipment, etc., the weighted value of the shortest distance was taken as the target coordinate. Tests show that the improved direction cosine method is effective, resulting in higher accuracy.

theodolite; direction cosine algorithm; intersection

2014-12-11

王颖(1972-),女,吉林白城人。工程师,硕士,研究方向:兵器工程研究。

TP274

A