直接地理参考中轨迹插值算法对精度影响的评估

宗文鹏，李广云，2，王 力，2，周阳林，2

直接地理参考中轨迹插值算法对精度影响的评估

宗文鹏1，李广云1，2，王 力1，2，周阳林1，2

( 1．信息工程大学导航与空天目标工程学院，河南郑州450052; 2．现代城市测绘国家测绘地理信息局重点实验室，北京100000)

一、引言

诞生于20世纪90年代初的移动测量系统( mobile mapping system，MMS)是当今世界最尖端的测绘科技之一［1］，具有精度高、速度快、可实时获取海量实景三维数据的特点，已在我国100多个数字城市信息化项目中得到成功应用。它代表着测绘与地理信息技术未来发展的一个重要方向［2］，将在地理空间数据采集与更新中发挥越来越大的作用［3］。MMS集成了定位定姿系统( position and orientation system，POS)、激光扫描仪及CCD相机等测量传感器，搭载在各种移动平台(汽车、火车、舰船等)上，可动态、实时获取航迹周围一定范围内目标的地理信息数据［4］。其中，POS主要由全球卫星导航系统( GNSS)、惯性测量单元( IMU)组成，分别提供载体在空间的位置和姿态信息，用于将测量传感器得到的结果直接转换到大地坐标系或指定的测图坐标系下，从而实现直接地理参考( direct geo-referencing，DG)。

摄影测量、遥感及扫描地图等得到的影像数据或激光扫描仪扫描得到的点云数据在用于成图或地理信息系统时，需要将其和真实的地理坐标进行匹配，即地理参考( Geo-referencing)。早期的地理参考通过地面控制点实现，称为间接地理参考( indirect geo-referencing)。随着卫星导航定位的发展，GPS辅助空中三角测量成为航空摄影中新的地理参考手段［5］。惯性导航与GNSS组合导航的出现使得测量能够在移动中直接实现数据的地理参考，称为直接地理参考［6］。车载移动测量系统的DG是指将三维激光扫描仪得到的目标点的角度和距离信息(或点坐标)通过一系列的坐标转换得到其地理坐标的过程。

POS系统中，GNSS接收机的频率较低，一般为1 Hz，IMU的频率相对较高，能达到上百赫兹，如Applanix公司的POS LV220为200 Hz，而随着硬件技术的发展，激光扫描仪的采样频率迅速提高，目前可达几百千赫兹，如Riegl的VQ-450二维激光扫描仪的采样频率达到550 kHz。在完成激光扫描仪时间同步后，可以得到激光扫描仪在每次采样时对应的测量系统的时间，但无法直接获得采样瞬间对应的测量系统的位置和姿态信息，因此存在内插问题。因为位置姿态信息存在于POS系统输出的轨迹数据中，故称之为轨迹插值。

文献［7—9］在分析移动测量系统误差模型时，都提到了位置姿态内插误差，但没有具体给出不同插值方法间的比较及其轨迹内插结果对激光脚点定位精度影响的大小。本文利用车载移动测量系统获取的实测数据，研究典型插值算法应用于轨迹数据插值的精度和效率，并根据车载移动测量系统整体误差模型给出插值结果对系统定位精度的影响大小。

二、典型插值算法

常用的代数插值算法有很多，如线性插值、抛物插值、拉格朗日插值、牛顿插值、自然样条插值等。

1．拉格朗日插值

n次插值问题，即求经过数据点( x0，y0)，( x1，y1)，…，( xn，yn)而次数不高于n的多项式，即

用构造n次插值基函数的方法，可得拉格朗日插值多项式为

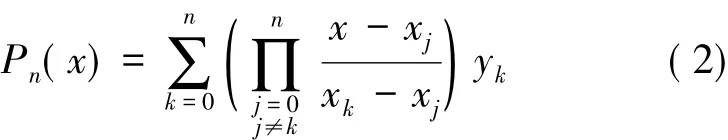
式中，n=1、n=2时分别对应线性插值、抛物插值。

2．牛顿插值

增加一个节点时，拉格朗日插值多项式除了要增加一项外，原来的每一项都要改变;而牛顿插值通过差商来构造插值多项式，当增加一个节点时，只需在原来的插值多项式中增加一项即可，其n次插值多项式为

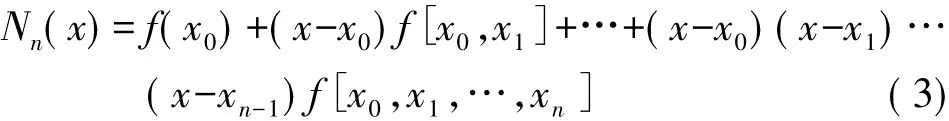
式中，f［x0，x1，…，xn］为f( x)关于节点x0，x1，…，xn的n阶差商。由插值多项式唯一性可知，Nn( x)≡Pn( x)。故牛顿插值多项式与拉格朗日插值多项式的插值余项相同，因此插值结果是相同的，但插值效率不同。

3．自然样条插值

在区间［a，b］上，已知函数y=f( x)在n+1个互异节点a=x0＜x1＜…＜xn= b处值为yi( i = 0，1，…，n)，若分段表示的函数φ( x)满足:

1)φ( x)在［xi，xi+1］的表达式φ( xi)都是不高于3次的多项式。

2)φ( xi) = yi。

3)φ( x)在整个区间［a，b］上有连续的二阶导数。

则称φ( x)为三次样条插值函数。但上述条件不足以确定其插值表达式，还需要加在区间两个端点处的边界条件，其中由自然边界条件

而得数称为自然样条插值函数。

三、测试数据及方法

轨迹数据为POS得到的结果，由一系列若干连续等时间间隔的点组成，每个点的数据主要包括UTC时间、里程、惯导坐标系原点的位置信息，以及三轴相对瞬时当地水平坐标系的旋转角。其中位置信息由X、Y、Z 3个坐标分量组成，姿态信息由3个姿态角组成，分别是侧滚角( roll)、俯仰角( pitch)和航向角( heading)［9］，数据还可包括原点的投影坐标、位置精度、角度精度等信息。其中，位置和姿态信息数据的精度在整个系统中起主导作用，因此本文在讨论插值算法的精度时只考虑这两方面的插值数据误差，本文采用的车载移动测量系统测得的每个点的数据中还包含经度( longitude)和纬度( latitude)两个值。

选择在郑州某测区的一次实测轨迹数据进行测试。试验进行了4次数据采集，其平均速度分别为5．5 m/s( 19．8 km/h)、12．2 m/s( 43．9 km/h)、17．7 m/s ( 63．7 km/h)和25．6 m/s( 92．2 km/h)。分别选取4种速度下的100个连续采集数据点，编号1—100。其中，奇数序号的点作为插值已知节点;偶数序号的点作为控制点(真值)以便评价插值精度。采用移动插值，即对每个待插值点，首先寻找其n个最近点，并求出插值函数，然后将该点的时间代入插值函数，得到相应量的插值结果。根据已知节点分别用不同插值算法得到对应控制点处的结果，与真值比较从而评价插值结果的精度。

测试包括拉格朗日插值取不同阶次的精度比较、不同插值方法间精度比较，以及各插值方法的效率比较。为评价插值的整体精度，定义两个精度指标:点位的插值误差mp、姿态的插值误差mθ，单位分别为米和度，即

四、各插值算法比较

1．不同阶次拉格朗日插值的比较

一般认为插值次数越高，所用节点越多，则结果越准确。但当次数较高时，多项式插值会出现龙格现象，使得插值结果不稳定。文献［10］指出，在进行高次插值时，越靠近端点逼近的效果越差。如图1所示，用高次插值得到的结果与真值在两端误差较大，在中间误差较小。

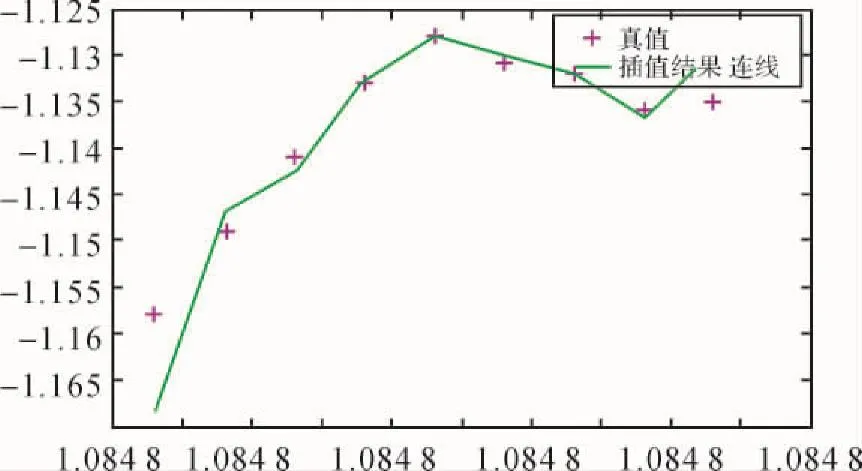
图1 高次插值龙格现象

通过加“窗”处理可以解决此问题，使插值点始终位于插值区间的中间，这样就可以保证插值的精度，且“窗口”尺寸越小效果越好［11］。取一段速度为25．6 m/s的包含100个数据点的连续轨迹，将奇数点作为已知节点，偶数点作为控制点(即待插值点)，比较不同阶次的拉格朗日插值结果。

为获得更好的插值精度，本文在测试时使“窗口”尺寸达到最小(即为零)即采用移动插值，且在插值区间两端增加了几个已知点。测试结果见表1。

表1 不同阶次n的拉格朗日插值精度比较

2．不同插值算法精度的比较

相同速度、不同速度下各插值算法计算结果分别见表2、表3。

表2 同一速度( 25．6 m/s)下不同插值方法精度比较

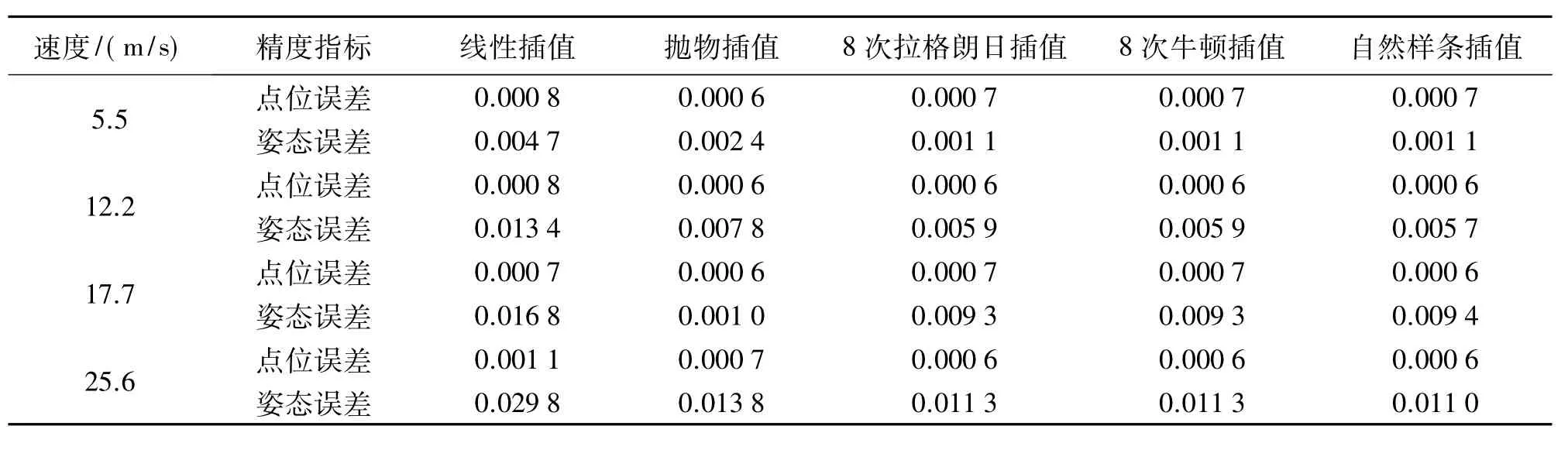
表3 不同速度下不同插值算法精度比较

3．不同插值算法效率的比较

待插值点151 353个，分别采用不同方法进行插值，VC++6．0中统计运行时间见表4。

表4 各插值算法运行时间 s

4．测试结果

由表1、表2可得，当拉格朗日插值阶次n≥8时，点位误差趋于稳定不再减小，而姿态误差在一定范围内随着插值阶次的增大而减小;相同轨迹数据采用自然样条插值到的点位误差和姿态误差分别为0．000 6 m和0．011 0°，可见适当提高阶次，拉格朗日插值可以得到与自然样条插值精度相当的结果。牛顿插值与拉格朗日插值效果等价，但插值效率相对较高;且在轨迹插值中一般都是等间距插值，采用差分代替差商，牛顿插值效率可进一步提高。

由表3可得，当车速提高时，插值结果的误差相应增大，但其中点位误差变化不明显，姿态误差变化较大。因此兼顾效率与精度，在低速时可对位置进行低阶次插值，对姿态进行较高阶次插值。由表4可知，随着插值阶次的提高，插值效率越来越低，而在相同精度要求下自然样条插值效率稍高。

五、结束语

由文献［7］可知，POS定位误差对激光脚点定位误差的影响是平移过去的，即直接传递的。如采用移动自然样条插值时，内插位置最大误差对激光脚点坐标造成的误差矢量为( 0．000 8，0．000 8，0．000 8) ;根据车载移动测量系统整体误差模型，在100 m范围内由内插姿态对激光脚点坐标造成的误差矢量为( 0．026，0．018，0．014)，则采用该插值方法对激光脚点坐标造成的点位误差为0．034 m，小于车载移动测量系统的整体误差，但与系统精度一样都是在厘米级上。

因此，兼顾精度与效率，可对位置与姿态数据分别采用不同插值方法，位置数据用移动线性插值得到即可满足精度要求，姿态数据用移动自然样条插值得到相比其他典型插值算法精度更高;姿态插值误差对系统精度影响较大，可尝试采用其他更好的插值算法进一步减小姿态插值误差。

［1］ 李德仁．移动测量技术及其应用［J］．地理空间信息，2006，4( 4) : 1-5．

［2］ 徐工，程效军．移动测量系统点云精度评定及应用分析［J］．工程勘察，2013，41( 9) : 42-46．

［3］ 王万峰，杜明义．MMS技术在城市户外广告景观数据采集中的应用［J］．测绘科学，2010，35( 5) : 199-201．

［4］ 张健源，李志刚．浅谈移动测量技术及其应用［C］∥中国测绘学会第九次全国会员代表大会暨学会成立50周年纪念大会论文集．北京:［s．n．］，2009．

［5］ 袁修孝，李德仁．GPS辅助空中三角测量的若干探讨［J］．测绘学报，1997，26( 1) : 14-19．

［6］ 邓忠军，杨娜，关艳玲，等．国产POS直接地理定位精度分析［J］．测绘科学，2012，37( 3) : 11-13．

［7］ 王丽英．面向航带平差的机载LiDAR系统误差处理方法研究［D］．阜阳:辽宁工程技术大学，2011．

［8］ 张小红．机载激光雷达测量技术理论与方法［M］．武汉:武汉大学出版社，2007．

［9］ 李鑫，李广云，王力，等．移动测量系统误差整体模型推导与精度分析［J］．测绘工程，2012，21( 2) : 21-24．

［10］朱琪．高次插值的龙格现象的测试［J］．湖南科技学院学报，2005，26( 11) : 206-208．

［11］仝海波，沙海，张国柱，等．一种GNSS卫星轨道高精度实时插值方法［J］．国防科技大学学报，2012，34( 2) : 59-63．

［12］ 冯有前．数值分析［M］．北京:清华大学出版社，2005．

Accuracy Evaluation of Trajectory Interpolation Algorithm in Direct Geo-referencing

ZONG Wenpeng，LI Guangyun，WANG Li，ZHOU Yanglin

移动测量中定位定姿系统的精度决定了整个系统的精度，为了获得激光扫描仪采样时对应测量系统时间点处的轨迹数据，需要进行插值。本文介绍了移动测量系统和直接地理参考，给出了典型的插值算法，以笔者所在学校车载移动测量系统的实测数据进行轨迹插值测试，对各种插值算法在不同移动速度下的轨迹插值结果的精度和效率进行了比较，并分析了对激光脚点定位精度的影响。结果表明，对位置进行移动线性插值，对姿态进行移动自然样条插值可以取得较好的精度和效率。

定位定姿系统;移动测量;轨迹插值;龙格现象;移动插值;自然样条

宗文鹏( 1990—)，男，硕士生，主要从事激光扫描仪应用的相关研究。E-mail: 524824358@ qq．com

P237

B

0494-0911( 2015) 11-0035-04

宗文鹏，李广云，王力，等．直接地理参考中轨迹插值算法对精度影响的评估［J］．测绘通报，2015( 11) : 35-38．

10．13474/j．cnki．11-2246．2015．0341

2014-11-16

国家自然科学基金( 41274014) ;现代城市测绘国家测绘地理信息局重点实验室开放基金( 20131204WY)