基于试验模态分析的某型号动车组齿轮箱有限元模态分析研究

张 骄 ，高小平 ，李 熙 ，谢 浩

(1．北京市地铁运营有限公司地铁运营技术研发中心，北京102208;2．北京南口轨道交通机械有限责任公司，北京102202)

0 引 言

齿轮箱是一个多自由度的振动系统［1］，作为动车组的驱动部件，也是动车组的关键部件，其运转状况直接影响到整车的正常运行。而且其工作环境恶劣，在工作时会受到外部激励［2］，产生振动，承受较大的载荷［3］。同时，齿轮作为齿轮箱的重要组成零件，其在啮合过程中也会产生冲击［4］，冲击力通过轴及轴承最终传递到齿轮箱体上［5］，从而引起箱体的剧烈振动［6］。一旦啮合频率与齿轮箱箱体的固有频率吻合或接近，齿轮箱就会产生共振效应［7］，这不仅影响齿轮的对中性［8］，也会加速齿轮箱的疲劳破坏［9］，故在设计齿轮箱时应避开共振效应。

模态分析技术是工程结构系统进行动力学分析的现代方法和手段［10-11］。对齿轮箱进行模态分析可为齿轮箱的动态特性、结构设计和性能评估提供一个强有力的工具;同时，根据模态分析的结果可进行模态参数识别，从而确定系统的模态固有频率、模态阻尼比及振型等。本研究以此对某型号的动车齿轮箱进行试验模态分析与有限元模态分析。

1 有限元模态分析原理

模态是机械结构的固有振动特性［12］，每一个模态具有特定的固有频率、阻尼比和模态振型［13］。模态分析是将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，然后解耦方程组得出结果［14］。齿轮箱箱体是一个连续的弹性体，为典型的线性定常系统，可视为小阻尼多自由度系统，其振动微分方程为:

式中:M—质量矩阵，C—阻尼矩阵，K—刚度矩阵;

式(1)为有阻尼的n 自由度系统的强迫振动微分方程，阻尼对结构的固有频率和振型影响不大，可以忽略阻尼作用，无外力作用时，则式(1)变为:

有非零解的充分必要条件是系数矩阵行列式等于零，即特征方程:

求解特征方程，即可得到系统的固有频率。

模态分析的目标是识别出系统的模态参数，为系统的振动特性分析、振动故障诊断和预报、结构动力特性的优化设计提供依据。

2 有限元模态分析结果

由于笔者研究的是表征结构整体特性的结构模态特性，故齿轮箱模型中的局部小特征对其影响较小，因此，在建立有限元模态分析模型时，对某型号齿轮箱模型进行必要的简化。忽略齿轮箱箱体结合处的影响，忽略箱体的倒角、圆角、进油孔、放油孔、螺栓孔等影响微小的局部区域结构。这样简化的建模过程不仅符合有限元建模的要求，也不会对箱体重量和结构整体刚度产生大的影响，同时也可以减少计算机的计算时间和计算耗费资源。

本研究采用三维软件SolidEdge 建立齿轮箱三维实体模型，进行必要的简化以后将模型导入到有限元分析软件ANSYS14．0 Workbench 中，利用其中的Modal 模块对齿轮箱进行模态有限元分析，得出其前12阶模态参数，齿轮箱前口阶自由模态如表1 所示。

表1 齿轮箱前12 阶自由模态

从第7 阶开始为箱体结构模态，振型如图1(a～f)所示，其中第1 阶振型为箱体轴向振动，第2 阶振型为箱体弯曲振动，第3 阶振型为箱体轴向振动，第4 阶振型为箱体摆动，第5 阶振型为箱体膨胀，第6 阶振型为箱体膨胀扭转耦合。

1.积极主动构建公众诉求的表达渠道和机制。要使各个利益主体能充分表达自己的要求和意见，从而在相互沟通中达到减少冲突、相互理解、相互包容或达成共识。当前，要全方位拓展社情民意的表达渠道，特别是注意倾听弱势群体的心声，为弱势群体建立自己正常、规范的利益表达机制，不回避矛盾，保证全体人民共享改革和发展成果，以促进和谐社会的建设。

图1 有限元模态分析前六阶模态振型图

3 试验模态原理

试验采用测量频响函数的方法来识别结构的模态参数，即:在敲击激励下，通过测量激励力f(t)和系统的响应输出x(t)，从而得到系统的频响函数:

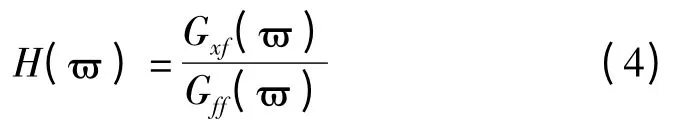
式中:H(ϖ)—频响函数;Gxf(ϖ)—力与响应的互功率谱;Gff(ϖ)—力激励的自功率谱。

对于任意的粘性阻尼的多自由度系统，其动力学微分方程为:

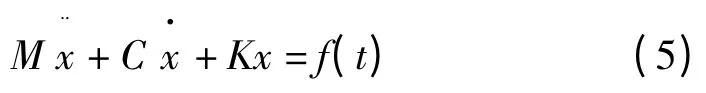
进行拉普拉斯变换得:

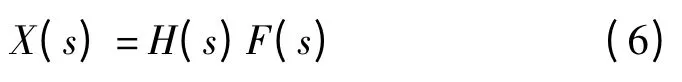
式中:

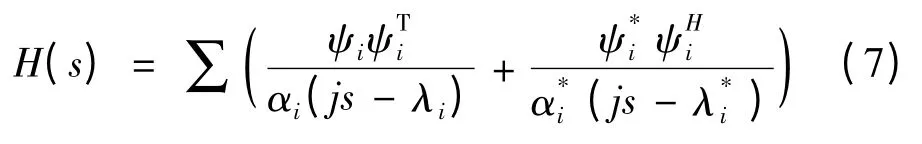
由式(4)得到的实测频响函数和式(8)频响函数的理论公式就可以确定结构的固有频率、阻尼比和振型。

4 试验模态过程

4．1 试验方案

本研究采用悬挂式锤击法，用力锤提供脉冲激励，采用单点激励多点响应的方式获取频响函数。具体测试模型如图2 所示。

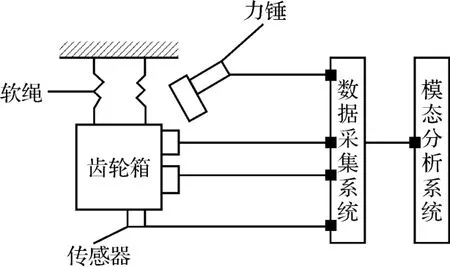
图2 测试系统框图

该实验用软绳吊起试件，软绳的伸缩频率在20 Hz以下，基本满足低于所测最低频率十分之一的要求，可认为试件处于自由状态。

试验通过敲击法获得其频响函数，共布置6 个测点，在试件径向布置4 个加速度传感器，轴向布置2 个加速度传感器，利用获得的频响函数对试件的模态参数进行识别。

4．2 激励点的选择

激励点的选择至关重要，它关系到试验件模态振型的好坏。在试验前应对齿轮箱作动态特性的预分析，预估试验件振型及固有频率，根据分析结构、激励方式、模态试验方法和试验人员的经验来选择激励位置。

该试验激励按51 个不同位置和不同方向的激励点分别进行，激励点示意图如图3 所示，对每个激励点敲击2 次。采集参数设置:分析频率2 048 Hz，每帧点数2 048。

5 试验模态结果

经多种识别方法对比分析，并排除局部模态影响，最终给出该型号齿轮箱六阶模态参数如表2 所示。

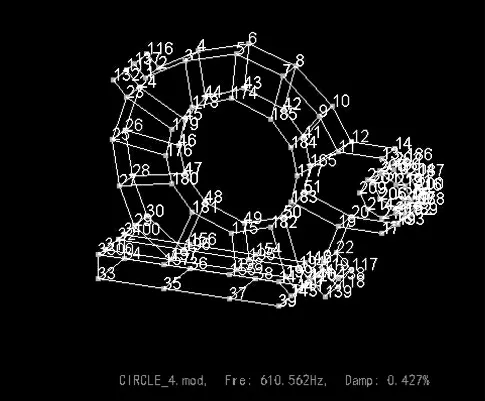
图3 激励点示意图

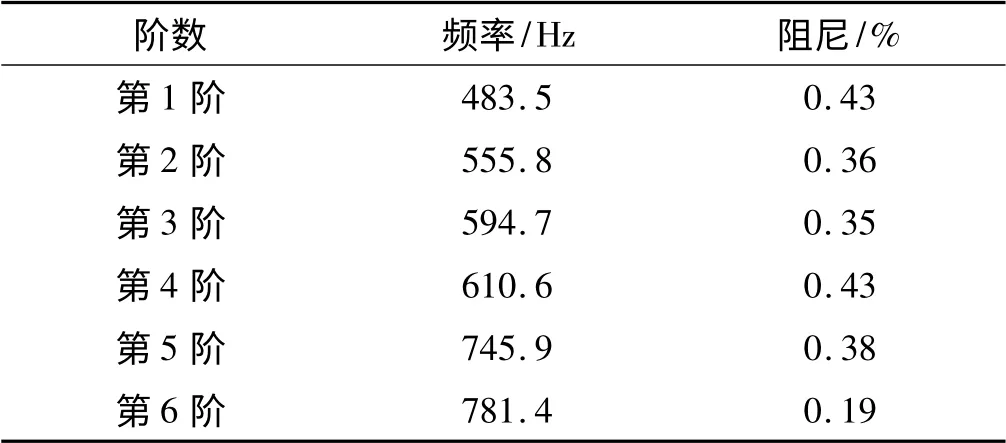
表2 齿轮箱前6 阶模态参数

各阶模态振型如图4(a～f)所示。

图4 试验模态分析前六阶振型图

其中，第1 阶振型为箱体轴向振动，第2 阶振型为箱体弯曲振动，第3 阶振型为箱体轴向振动，第4 阶振型为箱体摆动，第5 阶振型为箱体膨胀，第6 阶振型为箱体膨胀扭转耦合。与有限元模态分析结果是一致的。

6 有限元模态分析与试验模态分析结果

本研究对模态有限元分析方法结果与试验模态分析方法结果进行了对比，其结果如表3 所示。

表3 有限元模态分析方法结果与试验模态分析方法结果比对表

7 结束语

本研究通过对某型号的动车齿轮箱进行试验模态分析和有限元模态分析，得到如下结论:

(1)通过箱体有限元模态分析的振型以及试验实测分析出的振型，可以看出该型齿轮箱箱体的动态特性，为之后其结构的改进优化提供了理论依据。

(2)通过该型齿轮箱的有限元模态分析及试验模态分析的对比，发现有限元模态分析方法的结果与试验模态分析方法的结果非常相近，此举印证了有限元模态分析方法的可靠性，为之后的分析工作提供了实验基础及依据。

［1］张学亮． 齿轮箱模态分析和结构优化方法研究［D］． 太原:太原理工大学机械工程学院，2010．

［2］傅志方，华宏星．模态分析理论与应用［M］．上海:上海交通大学出版社，2000．

［3］杨晓宇．齿轮传动系统动力学特性的有限元分析及试验方法研究［D］．长春:中国科学院，2005．

［4］朱才朝，徐向阳，王海霞，等．大功率船用齿轮箱结构优化［J］．重庆大学学报，2008，31(11):1221-1225．

［5］凌桂龙，丁金滨，温 正．ANSYS Workbench 13．0 从入门到精通［M］．北京:清华大学出版社，2012．

［6］NAHVI H ，JABBARICRACK M． Detection in beams using experimental modal data and finite element model［J］．International Journal of Mechanical Sciences，2005 (47):1477-1497．

［7］CHOI J H． Shape design sensitivity analysis and optimization of general plane arch stuctures［J］．Finite Elements in Analysis and Design，2002(39):119-136．

［8］梁醒培，王 豪，张锴锋．大型齿轮箱结果分析与结构优化［J］．机械设计与制造，2008(1):31-33．

［9］尹逊民．传动齿轮箱体的振动模态分析及故障诊断［D］．哈尔滨:哈尔滨工业大学控制工程系，1999．

［10］曹树谦，张文德．振动结构模态分析-理论、实验与应用［M］．天津:天津大学出版社，2001．

［11］赵纯领，高洪滨，杜向华．基于振动信号的齿轮箱故障诊断［J］．机电工程技术，2014(6):102-104．

［12］沃 德，海 伦，斯蒂芬，等．模态分析理论与试验［M］．北京:北京理工大学出版社，2001．

［13］戴光昊，付金波，张海福．齿轮箱有限元模态分析及试验［J］．舰船科学技术，2010，32(8):167-170．

［14］范江东，潘宏侠．齿轮箱箱体的有限元模态与试验模态分析［J］．煤矿机械，2010，31(5):92-93．