两自由度非线性系统1:3内共振的渐近摄动分析*

胡海良 张伟

(1.北京工业大学机电学院，北京 100124)(2.浙江师范大学数理与信息工程学院，金华 321004)

引言

工程中许多模型的运动方程都可以表示成具有平方项和立方项的多自由度非线性系统，如复合材料层合板、功能梯度材料板的非线性振动.很多学者用不同的近似解析方法研究了这类系统的非线性动力学行为［1-3］.

通常情况下，非线性系统近似解的高阶项不会影响定性行为.然而，对具有平方项和立方项的非线性系统来说，必须求出高阶近似解以更准确地描述系统特征.Maccari［4］在暂态时间尺度和谐波平衡的基础上提出了渐近摄动法，它可以比较方便地把方程的平方项和立方项考虑进来.Zhang等［5］用渐近摄动法研究了主动电磁轴承的1:1内共振-主参数共振-1/2亚谐共振.Ye等［6］和Guo等［7］用渐近摄动法研究了复合材料层合板的非线性动力学行为.Hao和Zhang等［8］利用渐进摄动法研究了功能梯度材料板的非线性动力学行为.但是，渐近摄动法很难选择适当的设解形式，尤其是对1:3内共振情况，很容易因为设解不当导致精度很低.

本文通过引入一个新的设解形式，提出了一种改进的渐近摄动法.该方法是求解非线性系统的一种有效方法，它比原渐近摄动法求解过程更简单，并且更容易应用于1:3内共振情况.由于很多实际问题都可以用含平方项和立方项的两自由度非线性系统描述，我们用改进的渐近摄动法研究了这类系统在1:3内共振情况下的非线性动力学行为.与原方程数值结果对比表明，改进的渐近摄动法是研究两自由度非线性系统1:3内共振的有效工具.

1 渐近摄动分析

考虑如下两自由度非线性系统

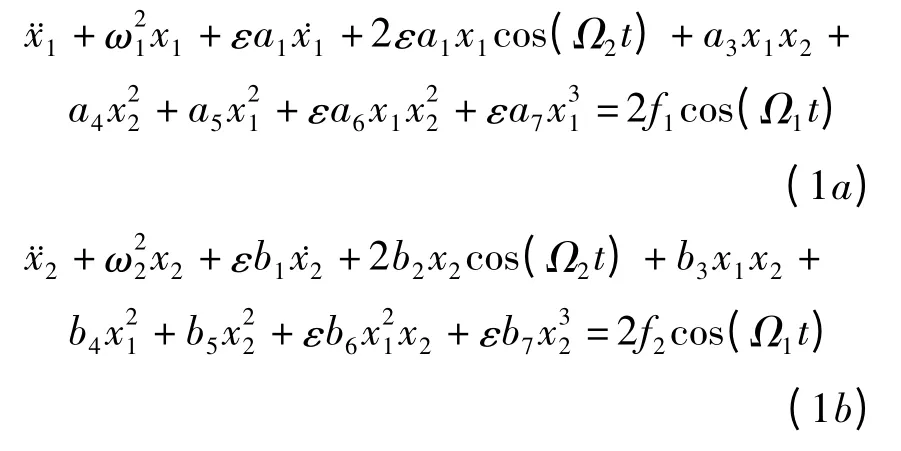
共振关系为

其中σ1和σ2为调谐参数，p1和p2为正有理数.

将方程(2)代入方程(1)中并令ε=0，得到派生线性系统具有简谐解

引进时间尺度变换

其中q为正有理数.

与派生系统的简谐解相比，由于非线性项、激励项和内共振的影响，方程(1)的解中将出现其它谐波项.同时各谐波项系数不再是常数，而是慢变时间尺度τ的函数.

假设方程(1)的解为

上述设解形式是在相应派生系统解的基础上给出的，除了ψ1(τ，ε)和φn(τ，ε)是O(1)之外，其他的谐波项系数ψn(τ，ε)和φn(τ，ε)都暂时设为O(ε)，具体阶次将在求解过程中确定.这样的设解形式使得改进的渐近摄动法更易于应用，并且能够适用于研究方程(1)的1:3内共振.而已有渐近摄动法设解形式中所包含的谐波项及其系数关于小参数的阶次都是事先给定的，因此很容易因为设解不当导致精度很低.另外，改进的渐近摄动法中不需要把函数ψn(τ，ε)和φn(τ，ε)展开成小参数ε的幂级数.简记ψn=ψn(τ，ε)和φn=φn(τ，ε).

将方程(5)代入方程(1)并令各谐波项系数等于零，可得关于ψn和φn的方程组.

当n=1时有

令p1=2，q=2并舍去ε的高次项得到

当n=3时有

令p2=2并舍去ε的高次项，得到

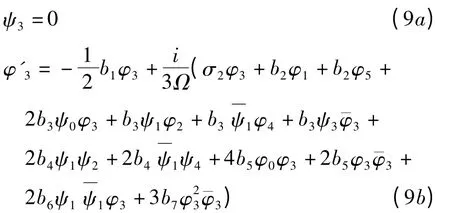
类似地，当n=0，2，4，5，6时有

由方程(6-14)得到关于ψ1和φ3的微分方程

其中

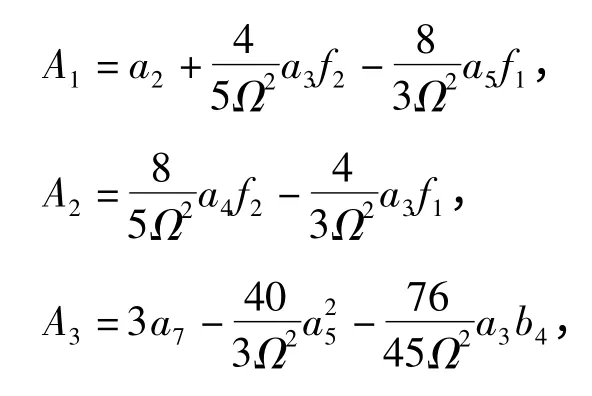
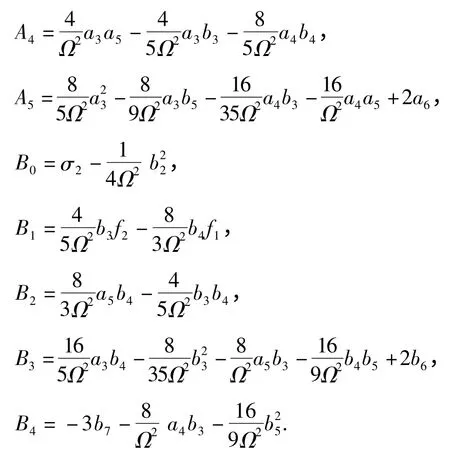
令

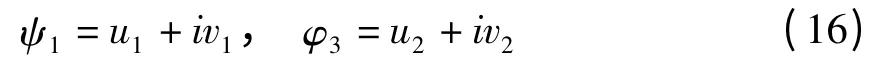
将方程(15)转变为直角坐标形式的平均方程

方程(1)的稳态周期解对应于方程(17)的平衡点.令

得方程(17)的平衡点应满足的非线性代数方程组.

2 数值对比

平均方程(17)经常被用来研究方程(1)的非线性动力学行为，下面我们将通过与数值结果对比考察近似解析解能够在多大程度上反映原方程的非线性动力学特性.

图1给出了当参数取值为ω1=1，ω2=3.01，f1=45，a1=8，a2=0.2，a3=0.1，a4=0.1，a5=0.5，a6=0.2，a7=0.2，f2=20，b1=8，b2=1.6，b3=0.8，b4=0.8，b5=3.5，b6=0.3，b7=5，ε=0.01时的幅频响应曲线.数值解初始值为［1，3，2，3］.图中红色的“×”表示直接由方程(1)得到的数值解，黑色的“.”表示由平均方程(17)得到的结果，两种结果基本吻合.

图1 幅频响应曲线Fig.1 The frequency response curves

当参数取值较小时，系统没有出现混沌现象.为了考察平均方程和原方程混沌运动的联系，我们将系统参数增大为ω1=0.5，ω2=1.502，Ω=1，a1=8，a2=2，a3=10，a4=10，a5=10，a6=1000，a7=2000，b1=8，b2=3，b3=10，b4=10，b5=10，b6=1000，b7=2000，f2=5.5，ε=0.01，此时系统分叉图如图2所示.所选取的初始值为［0.01，0，0.01，0］.其中图(a1)和(a2)由平均方程(17)得到，图(b1)和(b2)表示直接从方程(1)得到的数值结果，两种方法得到的分叉图基本吻合.

图2 随外激励幅值变化的分叉图Fig.2 Bifurcation diagrams with varying excitation amplitude

3 小结

本文用改进的渐近摄动法研究了两自由度非线性系统在1:3内共振情况下的非线性动力学行为.分别在平均方程和原方程的基础上作出了幅频响应曲线和分叉图.对比表明，改进的渐近摄动法是研究多自由度非线性系统1:3内共振的有效工具.原渐近摄动法很难选择适当的设解形式，尤其是对1:3内共振情况很容易因为设解不当导致精度很低.

1 Nayfeh A H，Jebril A E S.The response of two-degree-offreedom systems with quadratic and cubic nonlinearities to multi-frequency parametric excitations.Journal of Sound and Vibration，1987，115:83～101

2 Tien W，Namachchivaya N，Bajaj A.Nonlinear dynamics of a shallow arch under periodic excitation-I.1:2 internal resonance.International Journal of Non-Linear Mechanics，1994，29:349～366

3 郝育新，张伟，赵秋玲.复合边界条件下功能梯度板1:1内共振的周期与混沌运动.动力学与控制学报，2011，9:117～122(Hao Y X，Zhang W，Zhao Q L.Periodic and chaotic motion of mixed boundary FGM plate with 1:1 internal resonance.Journal of Dynamics and Control，2011，9:117～122.(in Chinese))

4 Maccari A.Approximate solution of a class of nonlinear oscillators in resonance with a periodic excitation.Nonlinear Dynamics，1998，15:329～343

5 Zhang W，Yao M H，Zhan X P.Multi-pulse chaotic motions of a rotor-active magnetic bearing system with time-varying stiffness.Chaos，Solitons＆Fractals，2006，27:175～186

6 Ye M，Sun Y，Zhang W，Zhan X P，Ding Q.Nonlinear oscillations and chaotic dynamics of an anti-symmetric cross-ply laminated composite rectangular thin plate under parametric excitation.Journal of Sound and Vibration，2005，287:723～758

7 Guo X Y，Zhang W，Yao M H.Nonlinear dynamics of angle-ply composite laminated thin plate with third-order shear deformation.Science China Technological Sciences，2010，53:612～622

8 Hao Y X，Chen L H，Zhang W，Lei JG.Nonlinear oscillations，bifurcations and chaos of functionally graded materials plate.Journal of Sound and Vibration，2008，312:862～892