基于CFD系统辨识的气弹分析及GPU并行算法初探*

黄灿 赵永辉

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

引言

颤振是飞行器气动弹性问题中的重要课题.传统气弹研究在亚声速上使用涡格法和偶极子网格法等频域方法可以得到较为精确的气动力解.而在跨声速时，以上方法不再适用.非定常CFD的方法可以进行大迎角、跨声速等非线性计算，在跨声速领域目前只有CFD方法计算最为精确［1］.然而，CFD计算所耗时间非常长，计算效率十分低下.

针对CFD计算离散化的特点，利用GPU并行计算可以天然地将任务划分成多份同时进行，大大的提高计算效率.GPU并行计算是近些年在计算领域快速发展的一项技术.GPU与CPU相比有着更强的单精度浮点计算能力和更宽的内存带宽［2-3］.在浮点运算上，GPU比CPU有着相当大的优势，同时期的GPU单精度浮点计算能力可达CPU的十倍.CUDA语言是GPU上的语言，可以通过CUDA命令调用GPU资源进行计算，实现计算的并行化［4-10］.

近些年系统识别也被应用到CFD计算中来，作为提高计算效率的另一种途径.目前有多种模型降阶(ROM，reduced-order model)方法，包括频域模型、时域自回归滑动平均模型(ARMA，auto-regressive-moving-average)和离散时间状态空间模型等［11-13］.CFD技术属于时域方法，本文选择ARMA模型来进行气动力建模.建立精确的非定常时域气动力降阶模型可以绕过繁杂的CFD流场求解器，直接根据输入输出关系得出想要的结果，这样可以大大降低计算所耗的时间.本文将这两种提高气动弹性分析效率的方法结合到了一起.首先利用GPU进行并行CFD计算，得到非定常气动力.然后利用非定常气动力识别出降阶模型.最后对降阶模型的精度进行了考核.

1 计算方法

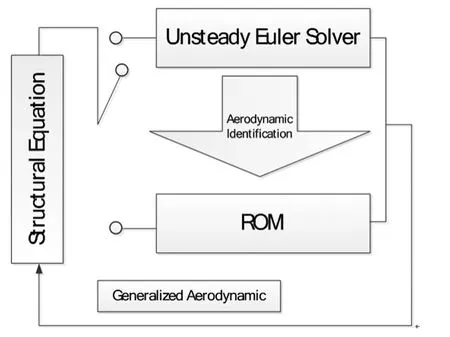
图1 基于气动力辨识技术的气动弹性仿真流程图Fig.1 Flow chart of aero-elastic simulation based on the identification of aerodynamic force

基于CFD系统辨识的气动弹性分析需要的流程如图1所示.其中非定常求解器求解所耗时间最多，本文将对这一部分进行并行化处理以提高效率.另外，对此部分进行系统辨识，得到降阶的气动力模型，再次提高计算效率.需要注意的是，不同的初始条件下辨识得到的非定常气动力降阶模型只能使用一次，初始条件改变则需要重新识别.例如，在广义气动力的计算中，不同马赫数的情况需要对应不同的降阶模型.

CFD计算部分采用Euler方程，守恒形式的Euler方程如下:

其中x和y为笛卡尔坐标系坐标，W为守恒变量:

F，G表示通量:

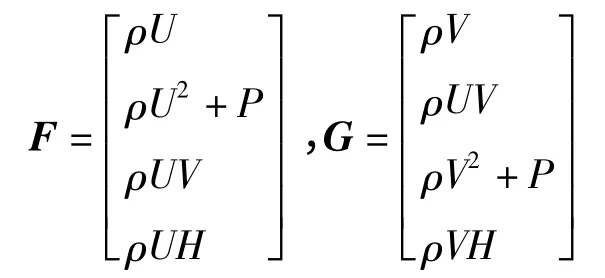
其中，ρ、P、H和E分别表示密度、压强、单元总焓和单元总能量.U，V分别表示笛卡尔坐标系下向x和y向的速度矢量.这些量由理想气体的单位体积的总能量E和总焓H互相联系，式中γ为比热比.

本文采用Jameson中心格式的有限体积法进行空间离散，利用双时间推进法进行时间离散.物理时间采用显示格式，拟时间采用四步龙格-库塔推进格式.网格使用的是非结构网格，动网格技术使用了弹簧法［14-18］.

气动弹性控制方程为:

式中M为质量矩阵，K为刚度矩阵，F为广义气动力向量，q为广义位移向量，它们分别可以表示为:

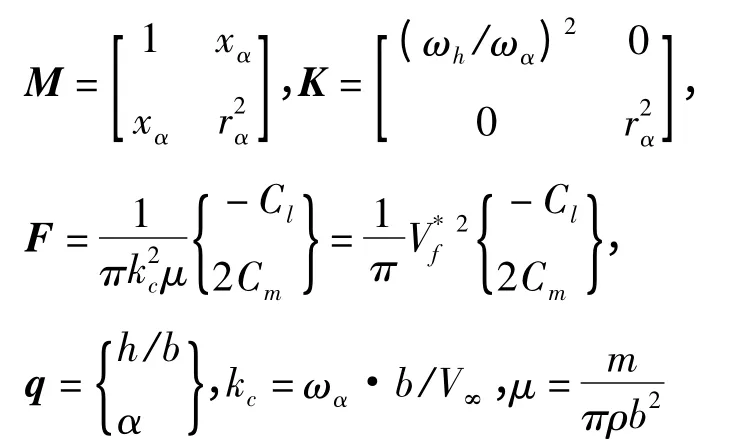
其中μ为质量比，Cl和Cm分别为升力系数和力矩系数，rα为机翼对刚心的无量纲回转半径，xα为重心与刚心的无量纲距离，ωα和ωh分别为俯仰和浮沉两个自由度的固有频率为无量纲颤振速度.

为了便于时域求解，引入状态变量E=(q1，q2，…，qN，˙q1，˙q2，…，˙qN)T，则方程(4)可以写成状态空间的形式:

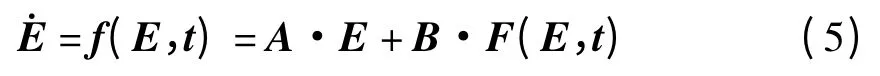
式中

在每个时间步内，将视为时间的单值函数，这样应用改进的龙格-库塔方法可将方程(5)展开为:

上式后几步中的F(t+Δ/2)和F(t+Δt)可用前几个时刻(F(t)，F(t-Δt)，F(t-2Δt))的值插值得到.该方法计算所得的精度要高于传统的冻结气动力的方法，而且在效率上大大超过标准的龙格-库塔方法.

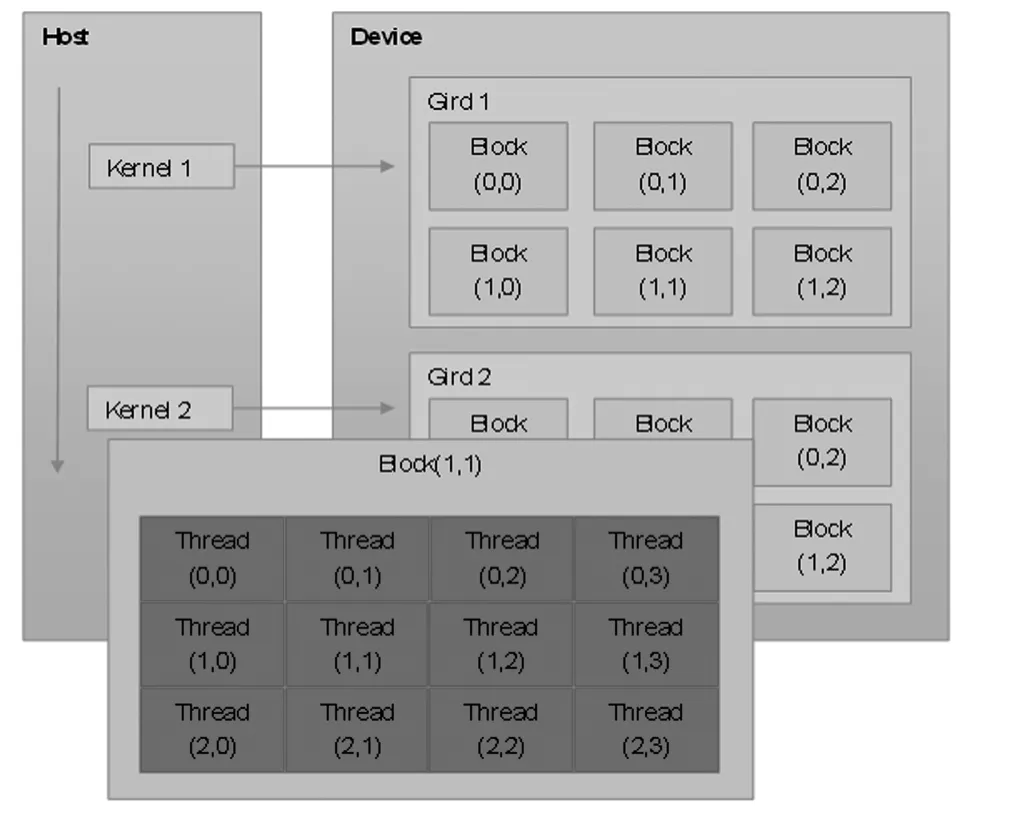
图2 GPU任务划分原理图Fig.2 The principle of division of tasks on GPU

GPU并行计算本文应用到CUDA语言和NVIDIA的GPU.并行计算的原理是将程序中的循环部分拆开，分别交给k(循环次数)个计算单元同时进行计算，再将计算结果读回主机端.GPU做并行计算有着天然的优势，其最小计算单元是线程，GPU中的线程数远远大于CPU中的核心数.其工作原理如图2:

并行计算要求各线程块和线程之间的计算互不干扰，于是随时间变化的迭代过程是不能够并行化的，因此只有适合的离散模型才能用GPU进行并行计算.非定常Euler方程中，多处进行了按单元或者按边循环的计算，这种空间离散模型在循环计算时同一时间步内边与边的计算相互独立，可以用GPU进行并行计算.随着网格单元数的上升，CPU计算时间大幅增加，而对于GPU的计算时间却增加很小.理论上并行部分的计算时间几乎不变，只是网格数的增加会增加一定的数据传输时间.于是对这些部分进行并行是可行的.其中主要包括通量和残值计算以及动网格计算的并行化.

图3 CFD计算流程Fig.3 Process of CFD

图3为CFD的计算流程，其中阴影部分均为可并行部分.本文将算例的CFD计算部分并行化处理，大大提高计算效率.本文计算的硬件环境为:Intel Core 2 Duo CPU，2.94GHz，4GB内存;NVIDIA Geforce GTX550Ti，192个流处理器(SM)，1GB显存.软件环境为Microsoft Windows7 SP1操作系统，VS2008编译器，CUDA版本为4.2.

系统识别采用ARMA模型.多输入多输出的ARMA模型实际上是系统的离散差分模型，其表达式为:

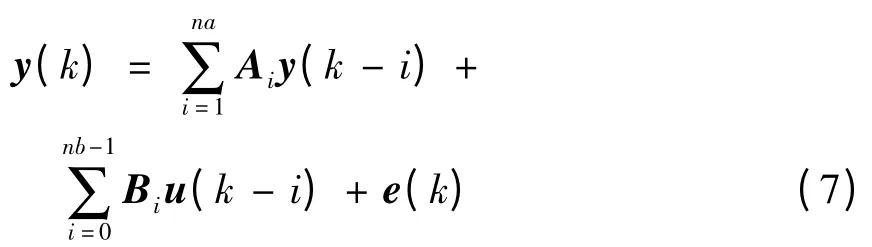
式中，y(k)为系统输出量(这里指广义气动力系数向量)的第k次观测值;y(k-1)为系统输出量的第k-1次观测值，以此类推;u(k)为系统第k个输入量(这里指广义位移向量);u(k-1)为系统第k-1个输入量，以此类推;e(k)为零均值的随机噪声;Ai和Bi为待辨识的参数矩阵;na和nb分别为输出和输入的延迟阶数.

设系统共采集了L组数据，即k=1，2，…，L，将式(7)化为如下方程:

式中:

根据最小二乘法，在随机噪声最小时，可得待识别参数矩阵θ的估计为:

本文选择了比较容易实现并且具有很宽频带宽度的“3211”速度输入.通过调整训练信号的时间步长，可以将频带移到试验所希望激发的频带上去.由于输入输出数据是一次性批处理的，故采用上文所述的一次性最小二乘估计，其精度较高.参数辨识需要对系统进行稳态清零，使系统满足零输入-零输出特性.

2 算例

为了验证流场求解器的正确性，首先选用NACA0012翼型进行非定常气动力计算，用计算结果与实验结果对比.以翼型的俯仰简谐振荡为例:

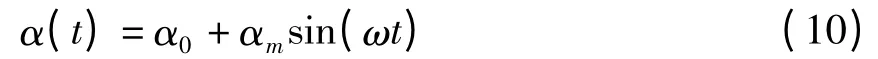
其中，初始攻角α0=0.016°，角度幅值αm=2.51°，角频率ω=k·V∞/b，缩减频率k=0.0814，半弦长b=0.5m，Ma=0.755.计算结果如图4所示:

图4 NACA0012翼型非定常气动力系数与实验值对比Fig.4 NACA0012 airfoil’s unsteady aerodynamic force simulation compared with experiment

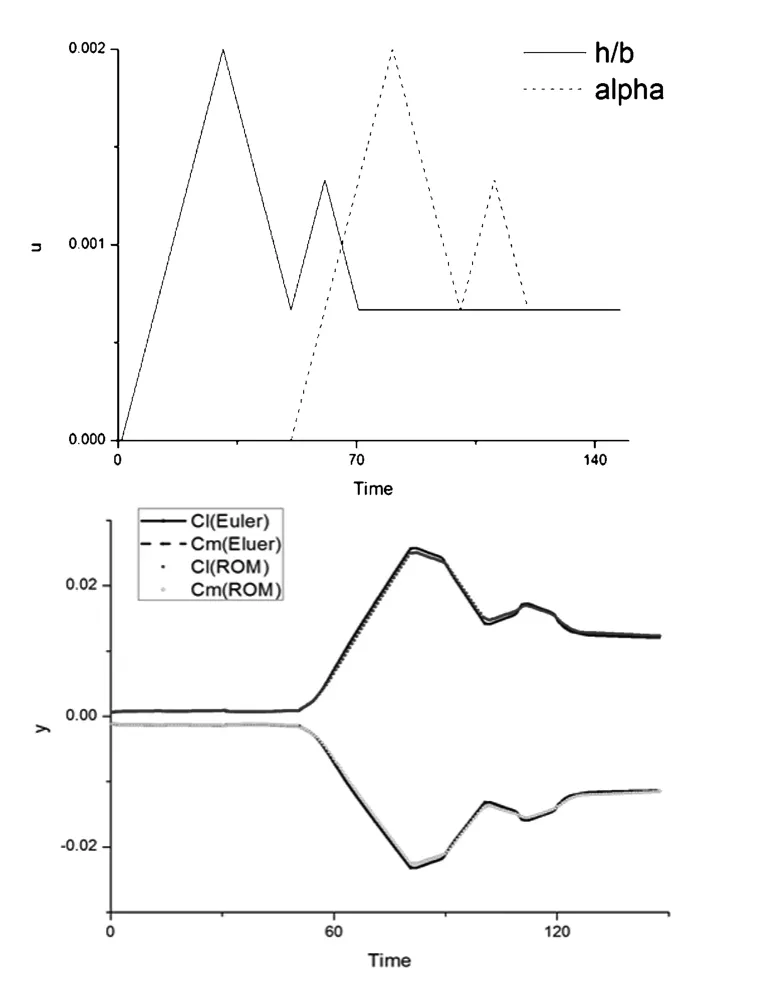
图5 3211信号输入下Euler解和降阶模型解比较Fig.5 The Euler solution compared with the ROM solution on 3211 input signal

颤振计算中本文选择了Isogai Wing，它是二维跨声速气动弹性计算的标准算例，其翼型为NACA64A010翼型.二元翼段气动弹性系统的物理参数为:

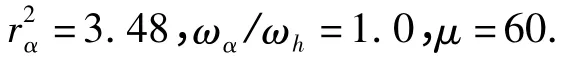
针对NACA64A010翼型，本文首先使用“3211”输入信号进行激励，通过调整输入信号的带宽和幅值将信号训练到合适的频带上来.训练信号包含了俯仰和浮沉两个自由度的输入，所得到的输出信号包括和两个系统输出.

图5中给出了“3211”信号输入下的Euler解和辨识模型解的比较.在相同输入下辨识模型给出的输出结果与非定常Euler求解器的输出结果吻合很好.可以看出，该辨识模型在很宽的频带范围内对原系统都有很好的近似.

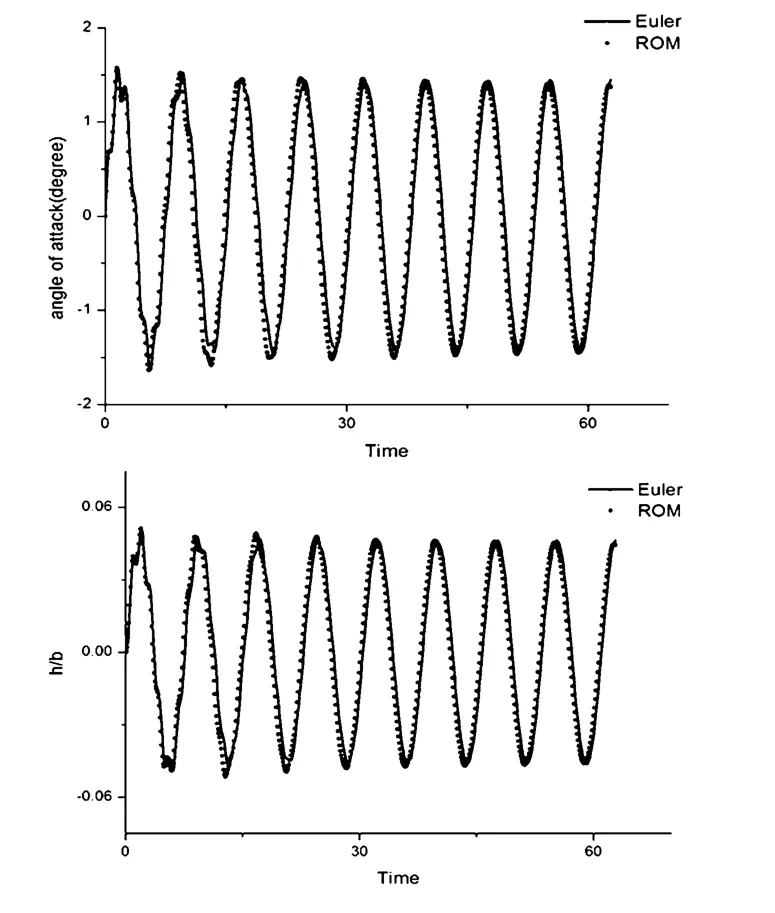
图6 NACA64A010翼型的颤振临界响应(Ma=0.825=0.54)Fig.6 The critical flutter response of NACA64A010 airfoil(Ma=0.825=0.54)

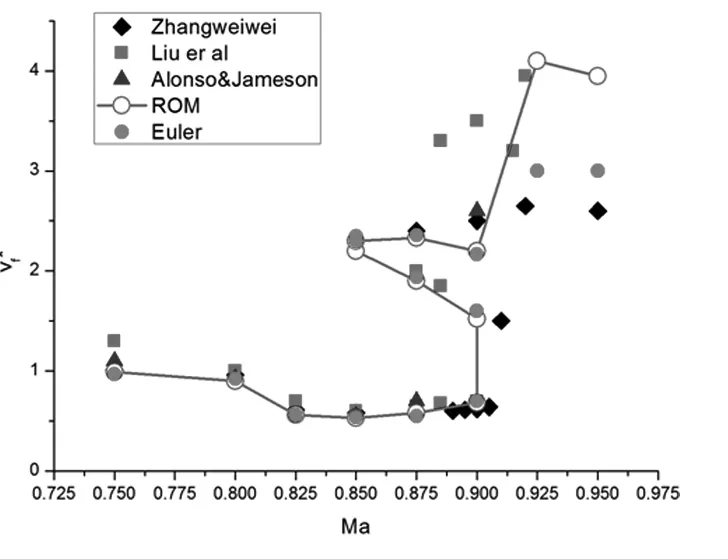
图7 NACA64A010翼型的颤振速度边界Fig.7 The flutter velocity boundary of NACA64A010 airfoil

针对Isogai Wing，算例计算了其颤振速度随马赫数变化的边界.图7中可以看出，与众多文献中的结果相比，基于非定常Euler方程的颤振速度边界和辨识模型计算的颤振边界在的状态下吻合的非常好.

CUDA语言的并行程序和串行C++程序计算的加速比约为2.8倍;ROM降阶模型与全阶CFD模型计算颤振速度加速比约为2.3倍;将并行程序和ROM降阶模型结合与全阶串行程序相比加速比约为6.4倍.对于二维翼型的计算，参考文献［10］中的结果来看，其应用CUDA语言并行计算得到了1.04倍的加速比，本文结果加速比更优.

表1 各方法下计算与原始程序计算加速比Table 1 The speedup of the program on different methods

3 结论

本文结合了两种非定常Euler方程的加速方法:基于CFD的非定常气动力采用GPU并行计算实现加速;之后利用CFD计算结果，得到了非定常气动力的ARMA模型.仿真结果表明ARMA降阶模型对原非定常气动模型还原较好，在保证了一定精度的情况下提升了计算效率.此外，CUDA并行程序受限于网格量并未发挥全部潜力，但优于文献［10］的二维结果，在三维问题上GPU并行计算对效率的提升将会非常可观.本文将两者结合可大大减少基于CFD的气动弹性计算时间，值得进一步深入研究.

1 张伟伟，叶正寅.基于非定常气动力辨识技术的气动弹性数值模拟.航空学报，2006，27(4)，579～583(Zhang W W，Ye Z Y.Numerical simulation of aeroelisticity basing on identification technology of unsteady aerodynamic loads.Acta Aeronoautica ET Astronautica Sinica，2006，27(4)，579～583(in Chinese))

2 张加乐.基于GPU并行计算的非定常Euler方程算法研究［硕士学位论文］.南京:航空航天大学，2012(Zhang J L.Numerical studies of unsteady euler equations based on GPU parallel computing［Master Thesis］.Nanjing:Nanjing University of Aeronautics and Astronautics，2012(in Chinese))

3 苗树明.NS方程在GPU上的并行实现［硕士学位论文］.上海:上海交通大学，2011(Miao S M.Implementation of NSequations in parallel on GPU［Master Thesis］.Shanghai:Shanghai Jiao Tong University，2011(in Chinese))

4 Corrigan A，Camelli F，Lohner R，Wallin J.Running unstructured grid based CFD solvers in modern graphics hardware.AIAA，2009:4001

5 Antoniou A S，Karantasis K I，Polychronopoulos E D.Acceleration of a finite difference WENO scheme for largescale simulations on many-core architectures.AIAA，2010:525

6 Brandvik T，Pullan G.Acceleration of a 3D euler solver using commodity graphics hardware.AIAA，2008:607

7 Shinn A F，Vanka SP，Hwu WW.Direct numerical simulation of turbulent flow in a square duct using a graphics processing unit(GPU).AIAA，2010:5029

8 Elsen E，LeGresley P，Darve E.Large calculation of the flow over a hypersonic vehicle using a GPU.Journal of Computational Physics，2008，227:10148～10161

9 Hargen T R，Lie K A，Natvig JR.Solving the euler equations on graphic processing units.Computational Science，2006，3994:220～227

10 张兵，韩景龙.基于GPU和隐式格式的CFD并行计算方法.航空学报，2010，2:249～256(Zhang B，Han J L.Parallel computing methods for CFD using a GPU and implicit scheme.Acta Aeronoautica ET Astronautica Sinica，2010，2:249～256(in Chinese))

11 Daniella E Raveh.Identification of computational-fluiddynamics based unsteady aerodynamic models for aeroelastic analysis.Journal of Aircraft，2004，41(3):620～632

12 Gupta K K，Bach C.Systems identification approach for a computational-fluid-dynamics based aeroelastic analysis.AIAA，2007，45(12):2820～2827

13 Lai K L，Won K S，Koh E P C，Tsai H M.Flutter simulation and prediction with CFD-based reduced-order model.AIAA，2012:2006～2026

14 Stolcis L，Johnston L J.Solution of the euler equations on unstructured grids for two-dimensional compressible flow.Aeronautical Journal，1990:181～195

15 John T Batina.Implicit flux-split euler schemes for unsteady aerodynamic analysis involving unstructured dynamic meshes.AIAA，1991，29(11):1836～1843

16 邓枫，伍贻兆，刘学强.基于混合动网格的二维非定常粘性流动数值模拟.南京航空航天大学学报，2007，39(4):444～448(Deng F，Wu Y Z，Liu X Q.Numerical simulation of two-dimensional unsteady viscous flow based on hybird dynamic grids.Journal of Nanjing University of Aeronautics＆Astronautics，2007，39(4):444～448(in Chinese))

17 王军利，白俊强，詹浩.基于非结构动网格的非定常气动力计算.飞机设计2005，9:24～29(Wang J L，Bai J Q，Zhan H.Calculation of unsteady flow using dynamic unsteructured grids.Aircraft Design，2005，9:24～29(in Chinese))

18 Jameson A.Time dependent calculations using multigrid，with applications to unsteady flows past airfoils and wings.10thAIAAComputational Fluid Dynamics Conference，1991:1596