基于spikes-LFP相关性的相位同步化研究*

朱雅婷 王如彬

(华东理工大学认知神经动力学研究所，上海 200237)

引言

神经元需要通过兴奋性或抑制性的突触连接产生功能性作用，所以Buzsáki提出网络中的神经元通过有规律地兴奋和抑制而引起同步振荡［1］.脑功能需要由负责该功能但分布广泛的神经元集群的动态交互来实现，因此信息整合涉及大尺度网络的同步化活动.Lakatos指出不同频率的振荡可以在同一个时刻在相同脑区中发生［2］，而Elbert和Rockstroh认为振荡相位的大小决定了神经元的兴奋程度，并且影响着网络中神经细胞在单位时间内的精确放电次数［3］.因此脑区之间神经元的相位关系显示了这些区域中动作电位的相对发放时刻.

相位同步化活动作为实现脑功能的一种重要的神经机制已经在许多认知神经科学实验中被证实［4，5，6，7］.这里的“同步化”是指脑皮层中两个区域的spikes之间的相关性，或者是一个区域上的spikes和相同区域或者不同区域上的LFP之间的动态耦合(即Spikes-LFP相关性)［8］.Womelsdorf在研究神经元交互作用时运用了上述同步化的概念［9］，而Viktor等人则提出时间的分散与延迟也会影响spike网络的同步化［10］.此外Benchenane在研究海马-前额叶皮层网络时，分析了两个区域中LFP的相位同步化(phase synchronization)，发现Spikes-LFP之间的相关性在相位同步运动与同步运动耦合区域(inter-regional)范围内具有正相关性［11］.

相位同步化在不同脑区中的不同表现形式具有其特殊的功能与生理学意义，受到研究者们的广泛重视.Montgomery在研究记忆任务的性能时，通过一个老鼠迷宫学习的实验揭示了gamma频段的同步化现象.当老鼠到达决策点时，CA1和CA3之间在gamma频段相位同步化会加强［12］.就同步运动的动力学机制而言，相位同步化的加强会促进CA1和CA3之间的神经交流和神经可塑性-这就是相位同步化的两大功能(如图1所示).

图1 神经元交流、神经元可塑性Fig.1 Neural communication and neural plasticity

Roelfsema等人在研究视觉信息整合时提出了神经元的交流与可塑性［13］，然后Engel等人在研究人脑活动的远距离同步化运动时提出gamma振荡的相位同步化可以增强神经信息流自下而上(从低级感官区到更高级的关联和控制区)和自上而下处理路径的神经交流［14］.Axmacher和Jutras等人发现相位同步化可以引发spike时间相关的可塑性［15，16］.Abbott以及Caporale等在各自对于可塑性的研究中都独立地提出了gamma频段中的相位同步化与动作电位的发放时刻有关，并且这类相位同步化运动能够促进spike时间相关的可塑性［17，18］.

Sun和Wang通过时间延迟来分析两类耦合离散时间网络之间的内在同步化和外在同步化［19］.Lu和Wang在运用HR神经元模型的基础上，加入噪声与神经元耦合因素，验证了耦合噪声神经元网络的同步发放，这为进一步得到相位同步化的模型打下基础［20］.Shen和Wang建立了一个简单的整合与发放的脉冲神经元模型［21］，配合STDP学习型神经网络，模拟了大鼠海马中位置细胞关于θ相位的神经编码，数值模拟结果与实验对照具有很高的准确率.最近Wang和Zhang利用随机相位动力学的方法，构造了几类神经网络模型［22，23，27］.依据文献［19，20］所建立的模型，在网络的拓扑结构发生变化的情况下，对具有多个神经元集群所构成的网络在自发运动和刺激作用下的相同步运动和神经编码的演化过程进行了计算机数值模拟.研究结果表明，(1)证明了神经科学实验中所揭示的脑内稀疏编码的存在性;(2)证明了神经系统内耦合系数的大小对于神经信息的处理至关重要以及神经信息传导在串联和并联两种耦合方式下所具有的完全不同的信息处理能力.(3)在外刺激作用下神经元集群内的神经元数目越大，刺激的结果对其他神经元集群的相同步运动和神经编码演化的影响也越大;(4)证明了神经生物学实验结果，神经元集群之间耦合关系的减小预示着神经网络中侧抑制功能的增强，这种增强等效于降低神经元的兴奋性阈值，从而使这一区域和神经元集群在相同的刺激下有较强的反应;(5)刺激作用下会有更多的神经元兴奋，因而有更多的神经元参与了神经编码和相同步运动.从而理论上再一次证明了神经交流和神经可塑性是可以互相支持的.这些研究成果还表明，当不同脑区通过相位同步化交流，会引发这些区域的突触可塑性;同时还表明当两个区域的突触连接加强，更容易引发相位的同步化运动从而促进脑区神经元之间的交流.Jutras等人在猕猴实验中发现，图片刺激呈现后，海马内的gamma频带spikes–LFP的相关性增强，从而体现了图片识别任务中的记忆性能［24］.研究结果反映了同步化对于spike依赖于时间的可塑性具有促进作用.高发放率细胞的spikes会集中在gamma频段中较窄的相位范围内(导致高Spikes-LFP相关性)，但是低发放率细胞的spikes会集中在theta频段中较宽的相位范围内(导致低Spikes-LFP相关性).

本文重点讨论如何运用Spikes-LFP的相关性分析来探究相位同步化问题.单个神经元与gamma频带构成同步化时会对应一个精确相位，该相位能够对进一步处理信息以及与时间相关的可塑性产生影响，而更强的神经元活性能够导致gamma频段上早期的spike-gamma带相位移动.本文所提出的分析方法是同步化研究的基础，能够为进一步研究相位偏移的神经动力学机制提供支持.运用上述研究方法可以分析得到spikes所集中发放的频段，spikes在神经振荡的特定相位处有规律地发放是同步化活动促进神经交流与可塑性的直观体现，Spikes-LFP相关性的强弱能够进一步对神经编码、神经竞争、神经可塑性产生影响.

1 模型介绍

Vinck等人在探索视皮层V1区中是否存在相位同步化现象时，给出了定量分析—运用相位锁定值来反应spike相位.对于由一个电极记录得到的每个spike而言，都独立于在其他电极中记录到的LFP数据段.每个LFP数据段乘以Hanning window再进行傅立叶变换，从而得到spike引发的LFP频谱.如下所述［26］:

其中xi(t)是spike i上LFP数据段的时间序列，I=1，2...，N，w(t)是Hanning window.接着将从其他电极中得到的M个LFP取平均(即:不是记录spike的那个电极)如下所述:

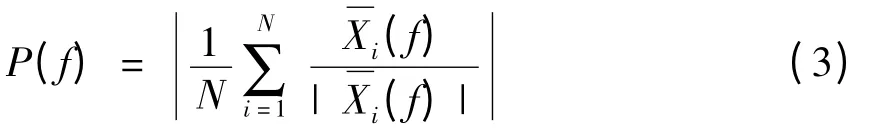
对于计算中用到的spike数量而言，spike–LFP相位-锁定值是有偏测量.因此，Vinck等人将含有不同数量元素的样本进行比较时，会把相同固定数量的spike加入到等式(3)中.另外，他们还运用自引导过程来化简spike–LFP相位锁定值的统计变量.对于每一个自举样本都要决定spike–LFP相位-锁定值，接着对在所有自举样本中得到的spike–LFP相位-锁定值取平均，从而得出“无偏”相位-锁定值.

我们将以上述模型为理论基础，运用Spikes与LFP的相关性来反映两者同步化情况.

2 数值计算结果分析

在研究相位同步化理论的基础上，我们提出一种研究同步化现象的方法，进而运用该方法去研究局部场电位(LFP)与神经元动作电位的发放(Spikes)之间的关系.数值计算基于Vinck等人所提出的相位锁定模型，改进后能够使Spike-LFP相关性分析法更具普遍性，主要步骤分为以下几个方面:1)提取实验数据;2)对所选取的LFP数据进行频谱分析，从而了解波形中所包含的各频段强度;3)对LFP数据进行滤波，留下所需的特定频段上的数据;4)实现在特定频段上LFP与spikes的相关分析;5)对相关性图进行数据拟合.

2.1 实验数据提取

由提取后的实验数据画出对应的LFP图、Spikes图.

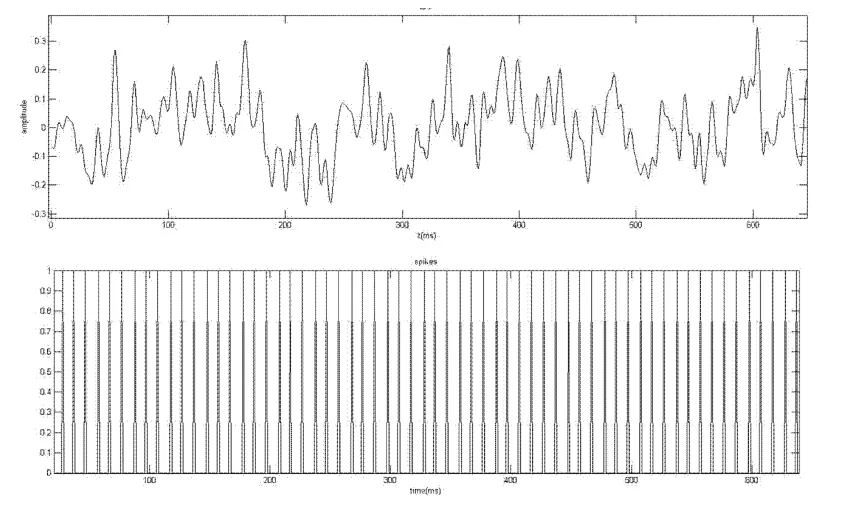
图2 LFP图和Spikes图Fig.2 LFP and spikes

图2中的上图显示的是一个刺激下单个实验中的LFP曲线，下图显示的是与LFP对应时间上的Spikes.

2.2 数据预处理

若直接对上述数据做相关性分析则所得到的Spike-LFP相关性曲线一直有频繁的上下浮动(图3)，也就是说在许多频率上都存在较多的相关性.这就表明LFP中包含较多频段的波，而spikes的发放又比较均一，从而spikes与LFP在许多频率上都存在相关性.

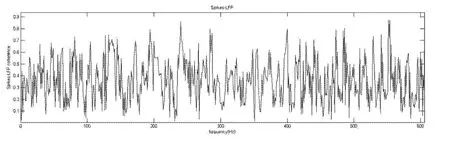
图3 Spikes-LFP相关性图Fig.3 Spike-LFP coherence

我们需要分析在一个频段上存在较高相关性而在其他频段上不存在较高相关性的情况，因此对数据进行预处理-对LFP进行频谱分析和滤波.

(1)频谱分析

神经元振荡的频率取决于不同的时间常量和网络性质，并且不同频率的振荡可以在同一个时刻在相同脑区中发生.通过傅里叶变换对LFP数据进行频谱分析可以具体了解到LFP振荡中所包含的所有频率成份，进而能够确定下一步所要分析的频段.

图4 LFP频谱分析图Fig.4 LFP spectrum analysis

图4为LFP的频谱分析图，如图所示LFP曲线在400Hz以后不存在频率成分，进一步放大该图得到图5，发现LFP曲线的频率成分主要集中在0-50Hz之间，也就是说我们将对这部分频段的波做进一步的分析.

(2)LFP滤波

运用matlab中的idealfilter函数对LFP进行滤波，进而得到LFP数据中在某一频段上的波.

图5 LFP频谱分析图Fig.5 LFP spectrum analysis chart

图6 滤波后的LFP波形图Fig.6 LFPwaveform after filtering

图7 Spikes-LFP相关性图Fig.7 Spike-LFP coherence

如图8所示，在200-400ms区间上，波形存在7个周期的振荡，从而该波包含35Hz频率成分;在800-1000ms区间上，波形存在6个周期的振荡，从而该波包含30Hz频率成分，而在所有区间上都存在类似的情况，所以滤波后得到是只含有30-35Hz频率成分的LFP波形图.但是在整体波形上仍包含较低频率的波，这对我们最终的相关性分析会造成一定的影响.也就是说可能在30-35Hz以外的频段上也存在一定的Spikes-LFP相关性.

2.3 Spikes－LFP相关性分析

通过Spikes-LFP相关性来反映两者的相位同步化情况.首先对Spikes进行离散数据傅里叶变化，对LFP进行连续数据傅里叶变化;接着计算得到Spikes的频谱S1，LFP的频谱S2以及两者的交叉频谱S12;最后用数值计算值C=abs(S12./sqrt(S1.*S2))来反映Spikes-LFP的相关性.

通过上述方法对滤波后的(30-35Hz)LFP和相应的Spikes做相关性分析从而得到Spikes-LFP相关性图.如图7所示30-35Hz频段内两者的相关性达到最高，即Spikes在该频段LFP的特定相位处会有固定发放，从而趋于同步化.但是在25-30Hz频段上相关性指数也超过了0.5，说明滤波还是存在着一定的误差，滤波的性能还有待提高.

2.4 拟合相关性曲线

为了更加清晰的呈现Spikes-LFP相关性的整体趋势，所以选出上述相关性曲线中的波峰进行置信区间95%高斯拟合，从而得到拟合相关性图(图8)

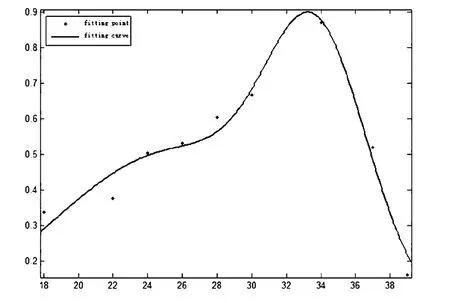
图8 拟合相关性图Fig.8 Fitting correlation

通过该项数据拟合可以更加直观的发现在32-35Hz区间内Spikes-LFP相关性达到最高，也就是说在该频带内Spikes在该频段LFP的特定相位处会有固定发放，从而趋于同步化.

3 结论

相位同步化机制在神经系统信息处理的过程中发挥着重要的作用.相位同步化的表现形式主要体现在脑皮层中不同区域spikes之间具有相关性以及同一个区域或不同区域之间spikes和LFP之间的耦合(称Spikes-LFP相关性)等.相位同步化的功能主要是促进神经元之间的交流以及通过神经交流增强神经元的可塑性，两者之间既可以互相支持也可以相互影响.值得注意的是，单个神经元的spikes与LFP构成同步化时会对应一个精确的相位，该相位能够对进一步处理信息以及与时间相关的可塑性产生影响.本文基于相位同步化理论，提出了一种研究同步化现象的方法，即通过研究局部场电位(LFP)与Spikes之间的相关性的大小来判定区域的同步化情况.研究过程中首先对实验数据进行预处理，通过频谱分析了解LFP中所有频率成份的分布情况，从而确定含有较高频率成份的频段，接着通过滤波来获取该频段，从而确保LFP与spikes分析的有效性.对预处理后的LFP与spikes的数据进行相关性分析，从而精确定位到两者之间在某一频段存在高度的相关性，也就是说Spikes在该频段LFP的特定相位处会有固定发放，从而趋于同步化.

我们所提出的Spike-LFP相关性分析法的优点在于，通过预处理能够初步确定存在Spike-LFP相关性的潜在频率范围，大量减少了不必要的数据分析过程，从而提高了数据分析的效率，也使其下一步的相关性分析更具针对性.Vinck等人在进行Spike-LFP相关分析时，主要是通过多个电极记录各位置单个spike引发的LFP数据，并对LFP数据进行平均以及数值计算从而得到spike-LFP相位锁定值，以该值的大小来反映相关性的大小，该分析方法对信号记录的要求较高、且需要特殊的数据预处理步骤，若前期分析达不到要求则对相关性结果影响较大.我们在进行Spike-LFP相关性分析时，从spike数据与LFP数据两者出发，进行各自频谱分析以及交叉频谱分析，对上述三项分析结果进行数值计算从而得到Spike-LFP相关性，因此该方法在不降低可靠性的前提下使用更加方便，从而更具普遍性.

具有较高相关性的频带所包含的生理学意义在于，它将对进一步处理信息以及与时间相关的可塑性产生影响，从而能够更深入的揭示神经信息处理以及认知功能等形成的动力学机制.所以确定存在较高Spikes-LFP相关性的频带对于了解神经系统的同步化运动具有重要的意义，有助于我们对该系统中的同步化问题作更深入的研究.Spikes-LFP的相关性分析作为整个同步化研究的基础，能够为进一步研究相位的偏移(phase shifting)提供支持［28］，并且有助于从复杂的相位神经编码中提取有用信息，减少冗余.本文中所提出的相位同步化的研究方法将不仅有利于解释和验证神经信息处理的工作方式、运作机制，也有利于探索新颖的计算方法和功能结构，以期应用于各个科学与工程领域.

1 Buzsáki G.Rhythms of the brain.Oxford:Oxford University Press.2006

2 Lakatos P，et al.An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex.Journal of Neurophysiol，2005，94:1904～1911

3 Elbert T，Rockstroh B.Threshold regulation-a key to the understanding of the combined dynamics of EEGand event-related potentials.Journal of Psychophysiol，1987，4:317～333

4 Siegel M，Warden M R，Miller E.Phase-dependent neuronal coding of objects in short-term memory.Proceedings of the National Academy of Sciences of the United States of America，2009，106(50):21341～21346

5 Sato N，Yamaguchi Y.Spatial-area selective retrieval of multiple object-place associations in a hierarchical cognitive map formed by theta phase coding.Cognitive Neurodynamics，2009，3(2):131～140

6 Colliaux D，Molter C，Yamaguchi Y.Working memory dynamics and spontaneous activity in a flip-flop oscillations network model with the Milnor attractor.Cognitive Neurodynamics，2009，3(2):141～151

7 Wagatsuma H，Yamaguchi Y.Neural dynamics of the cognitive map in the hippocampus.Cognitive Neurodynamics，2007，1(2):119～141

8 Fries P，Reynolds J H，Rorie A E，Desimone R.Modulation of oscillatory neuronal synchronization by selective visual attention.Science，2001，291:1560～1563

9 Womelsdorf T，et al.Modulation of neuronal interactions through neuronal synchronization.Science，2007，316:1609～1612

10 Viktor K.Jirsa，dispersion and time delay effects in synchronized spike–burst networks.Cognitive Neurodynamics，2008，2(1):29～38

11 Benchenane K，et al.Coherent theta oscillations and reorganization of spike timing in the hippocampal-prefrontal network upon learning.Neuron，2010，66:921～936

12 Montgomery SM，Buzsáki G.Gamma oscillations dynamically couple hippocampal CA3 and CA1 regions during memory task performance.Proceedings of the National Academy of Sciences，2007，104:14495～14500

13 Roelfsema P R，Engel A K，König P，Singer W.Visuomotor integration is associated with zero timelag synchronization among cortical areas.Nature，1997，385:157～161

14 Engel A K，Fries P，Singer W.Dynamic predictions，oscillations and synchrony in top-down processing.Nature Reviews Neuroscience，2001，2:704～716

15 Axmacher N，Mormann F，Fernández G，Elger CE，Fell J.Memory formation by neuronal synchronization.Brain Research Reviews，2006，52:170～182

16 Jutras M J，Buffalo E A.Synchronous neural activity and memory formation.Current Opinion in Neurobiology，2010，20:150～155

17 Abbott L F，Nelson S B.Synaptic plasticity:taming the beast.Nature Neuroscience，2000，3:1178～1183

18 Caporale N，Dan Y.Spike timing-dependent plasticity，a Hebbian learning rule. Annual Reviews Neuroscience，2008，31:25～46

19 Sun W G，Wang R B，Wang W X，Cao J T.Analyzing inner and outer synchronization between two coupled discrete-time networks with time delays.Cognitive Neurodynamics，2010，4(3):225～231

20 Shi X，Wang Q Y，Lu Q S.Firing synchronization and temporal order in noisy neuronal networks.Cognitive Neurodynamics，2008，2(3):195～206

21 Shen E H，Wang R B.A spiking neuron model of theta phase Precession.Lecture Notes in Computer Science，2006，4221:214～223

22 Wang R B，Zhang Z K.Phase synchronization motion and neural coding in dynamic transmission of neural information.IEEE Transactions on Neural Networks，2011，22(7):1097～1106

23 Wang R B，Zhang Z K.Neural coding in networks of multi-populations of neural oscillators.Mathematics and Computer in Simulations，2012，86:52～66

24 Jutras M J，Fries P，Buffalo E A.Gamma-band synchronization in the macaque hippocampus and memory formation.Journal of Neuroscience，2009，29:12521～12531

25 Juergen F，et al.The role of phase synchronization in memory processes.Journal of Neuroscience，2011，12:105～118

26 Vinck M，et al.Gamma-phase shifting in awake monkey visual cortex.Journal of Neuroscience，2010，30(4):1250～1257

27 王如彬，张志康，谢智刚，焦贤发.多个神经振子群网络的相位动力学编码.动力学与控制学报.2009，7(3):217～225(Wang R B，Zhang Z K，Xie Z K，Jiao X F.Dynamic coding of phase on multi-populations of neural oscillators.Journal of Dynamics and Control，2009，7(3):217～225(in Chinese))

28 沈恩华，王如彬，张志康.θ相移在单次学习过程中促进神经网络对空间位置顺序记忆的研究.动力学与控制学报，2009，7(2):183～187(Shen Y H，Wang R B，Zhang Z K.θphase shift in a single neural network to promote the learning process in order for the spatial location of the memory.Journal of Dynamics and Control，2009，7(2):183～187(in Chinese))