基于改进粒子群算法的薄板件定位策略优化

张 恒，邢彦锋

(上海工程技术大学汽车工程学院，上海 201620)

基于改进粒子群算法的薄板件定位策略优化

张 恒，邢彦锋

(上海工程技术大学汽车工程学院，上海 201620)

目前薄板件定位策略优化需要进行大量的有限元分析，限制了夹具设计的效率。为了减少有限元分析次数，提出了一种基于惯性权值的粒子群改进算法，并通过对有限元软件的二次开发将该优化算法应用于夹具定位点的优化设计当中，以某车身前翼子板为实例进行了夹具定位优化设计，结果表明了方法的有效性。

车辆工程;金属薄板;粒子群算法;定位策略优化

张 恒，邢彦锋.基于改进粒子群算法的薄板件定位策略优化［J］.河北科技大学学报，2015，36(3):300-305.

ZHANG Heng，XING Yanfeng.Optimization of sheet components locating scheme based on improved particle swarm optimization［J］.Journal of Hebei University of Science and Technology，2015，36(3):300-305.

冲压加工以其较高的生产率和材料利用率，广泛应用于汽车、飞机和各种家用电器制造工业，冲压件的焊接装配成为上述产品制造的关键工序，焊装夹具的性能不仅影响到生产率，而且直接关系到产品的质量。因此如何有效地减少和控制定位误差的影响，对提高焊装质量至关重要。在薄板零件的装配过程中，夹具定位策略和焊点位置等因素对装配偏差的影响往往会超过零件本身的制造偏差［1］。据克莱斯勒公司报告，每增加1个定位点，将会增加约10 000美元的成本，因此在满足装配公差的条件下通过调整夹具定位位置减少定位点数量是夹具定位策略优化的重要内容。

针对薄板零件的特点，CAI等［2］提出了一种“N-2-1”定位，并证明了该定位原理与六点定位原理相比更适用于易变形薄板零件的定位。CAMELIO等［3］在有限元分析的基础上应用非线性规划算法对薄板零件的定位点进行了优化。LI等［4］针对薄板零件夹具定位的特点，建立了基于多项式函数的两阶段响应面模型进行夹具定位方案优化。CARLSON等［5］应用二次灵敏度方程进行夹具定位策略的优化，VISHNUPRIYAN等［6］采用遗传算法优化夹具定位点。XING等［7］应用two-stage方法进行夹具定位策略优化。然而以上方法并未对算法参数的取值方法进行改进。本文在以上研究成果基础上，提出了一种基于惯性权值的改进粒子群算法(PSO)，通过改进惯性权值取值方法，提高算法搜索效率，减少夹具定位点优化时有限元分析的计算次数。

1 夹具定位策略及评价函数

在薄板零件装配过程中，本文应用“N-2-1”夹具定位策略减少零件在第1基准面上的变形。“N-2-1”定位原理认为，对于薄板件而言，最合理的夹具系统是要求其第1基准面上存在多于3个定位点，去限制这一方向上的零件变形。第2、第3基准面所需的定位点为2个和1个，去限制薄板件的刚体运动［8-11］。第2、第3基准面上定位点的布置如图1所示。第1基准面上定位点的位置由粒子群算法优化生成。对于尺寸不大的零件而言，可取N值为4。

本文使用金属薄板件进行有限元分析，设薄板的尺寸为150 mm×150 mm×1 mm，杨氏模量为 2.07×105N/mm2，泊松比为0.3。在零件表面施加适当的均布力，计算不同夹具定位方案下各关键测点在主平面内的法向位移;其中划分网格为15×15，共256个节点，为了评价各个夹具定位策略的优劣，采用零件表面所有测点在主平面内的法向位移绝对值之和作为评估函数，即:

图1 金属薄板零件网格Fig.1 Mesh of sheetmetal components

式中:F(X)为夹具定位策略优化的目标函数;X表示夹具定位点所组成的向量;N为薄板件上关键测点的数目;ωi是第i个点的挠度。

2 夹具定位策略优化方法

本文应用一种基于惯性权值的改进粒子群算法对薄板件进行定位策略优化。粒子群算法最早由Kennedy和Eberhart观测一些动物的行为后提出，例如鸟扑食行为。粒子群算法利用群体解决方案，每个方案称之为粒子，它在其搜索空间内给出随机初始值，然后通过每个粒子的适应度值函数选择和更新粒子，最后得到所需要解决问题的最优解。粒子群算法通过群体优势解决优化选择问题，相对于遗传算法，粒子群算法的收敛速度更快，并且对较好的粒子有记忆功能。

2.1 粒子编码和解码

粒子群算法通过群体方法进行优化，其基础为粒子群。本文采用实数编码方式，网格节点编号组合即为粒子编码，4个节点号组成1个粒子。如图2所示，主定位平面内的4个定位点的节点号分别为109，151，182，240，则由这4个节点所组成的1个粒子编码为(109 151 182 240)。这种编码方式简单、高效，易于程序实现。得到节点编号后可通过读取inp文件来得到定位点的坐标，最终通过定位点坐标计算得到各个定位点的位置。

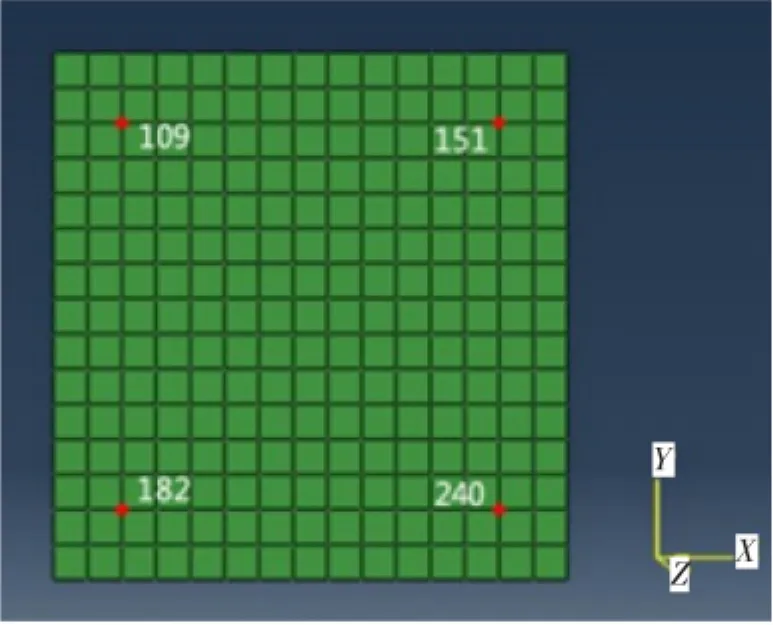
图2 定位点示意图Fig.2 Schematic diagram of locating point

2.2 基于惯性权值的改进

目前惯性权值的改进方法主要有惯性权值线性递减法、模糊惯性权值法、随机惯性权值法、惯性权值自适应调整策略等方法［12-17］。

惯性权重系数起到平衡两种搜索能力的作用，惯性系数ω大，全局探索能力强，能探索更大的新空间;惯性系数小，局部探索能力强，能在最优解的附近精细探索空间［18-22］。对于任何一种搜索优化算法，都希望早期有较强的全局探索能力，能发现好的解;而在搜索的晚期，则希望有较强的局部搜索能力，能够精细搜索较好解的局部空间。本文提出了一种惯性权值混合取值方法，即算法前期采用随机取值法，后期采用线性递减法。随机惯性取值法在算法前期能够加速粒子的收敛，且对大部分优化函数都能找到相当好的解，但后期容易越过最优粒子位置;线性递减法后期惯性系数较小，可在局部进行精细搜索，弥补了随机惯性取值法后期的不足。本文提出的混合法可以将两者的优点集于一身，以更好的搜索效果逼近全局最优解。ω计算公式见式(2):

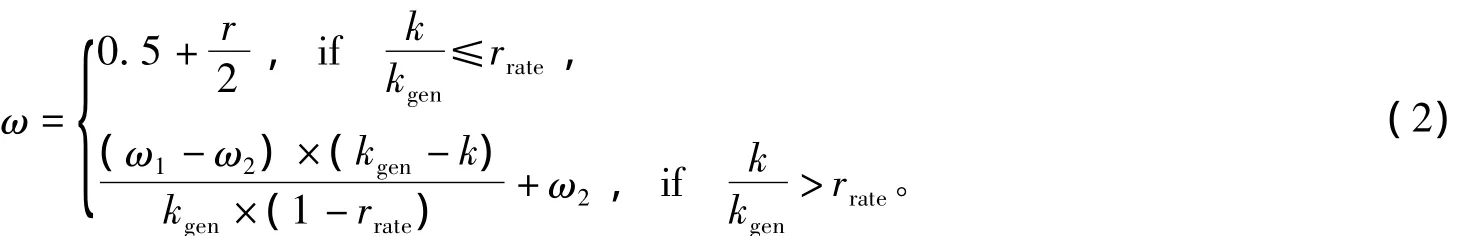
式中:r为［0，1］的随机数;kgen为总迭代次数;rrate为随机惯性权值法在整个算法过程中所占的比例，其取值范围为［0，1］;k为当前迭代次数;ω1，ω2分别为惯性权值的初始值和终值。可通过调整rrate值来调整随机惯性权值在整个算法中所占的比例。

2.3 粒子位置和速度更新

粒子群算法是通过更新每个粒子的位置来产生新的粒子群。针对定位点的特点，产生新粒子步骤如下。

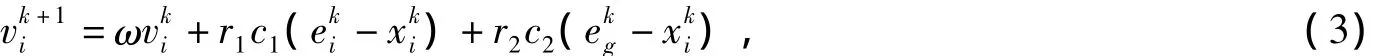
式中ω由本文所提出的混合惯性权值取值方法确定。参数 r1和 r2为［0，1］区间内的随机数，设置c1=c2=2，k为进化代数。个体最优值的更新为

Step2 更新粒子位置。粒子的位置为当前粒子位置和粒子速度之和，其公式见式(5):

当粒子的位置大于节点编号上界时，取编号上界，当粒子位置小于节点编号下界时，取编号下界。

2.4 粒子群算法流程

粒子群算法通过群智能解决优化问题，每次迭代通过个体最优解和全局最优解更新粒子的速度和位置，其停止条件是设置最大迭代次数或全局最优位置满足预定最小适应阈值。假设在D维空间中，粒子种群数量为M，粒子群算法流程如下。

Step1 参数初始化。初始化代数计数器k=0，每个粒子的位置为，速度为

Step2 评估粒子。由式(1)计算每个粒子的适应度值，适应度值越小则表示该定位策略越好;计算当代粒子群最优个体Pbest;计算全局最优粒子Gbest。

Step3 判断是否满足迭代停止条件，如果满足，则优化算法停止;否则转到Step4。一般优化算法的停止条件主要有2个:1)设置最大进化代数;2)对于所有粒子评估函数的均值变化，若每代粒子群的适应度函数均值之差小于10-2，则表示可停止该算法。

Step4 产生新粒子群。应用式(3)更新每个粒子的速度;应用式(4)更新每个粒子的位置;应用式(5)更新粒子;设置k=k+1。

Step5 重复Step2—Step4。

2.5 薄板零件定位点优化

针对如图2所示的薄板零件主平面4个定位点优化，一般种群粒子数为粒子自身维数的5～10倍，故本文设置种群大小N为20，设置粒子群算法2个迭代停止条件，根据粒子群优化流程，当惯性权重ω分别以混合法和线性递减法取值时，其适应度值的优化曲线如图3所示。由图3可以看出，当ω以线性递减法取值时，由于ω的值不断减小，使得算法的全局搜索能力不断减弱，最终在计算到第25代左右时陷入局部最优解，导致粒子停止进化;而本文所提出的混合惯性权值法在算法一定的计算次数内(本文设定为25次)，能够一直以较好的全局搜索能力在全局范围内进行搜索，图中通过与线性递减法的对比可知，在前25代内，混合法有更强的全局搜索能力，结果更接近全局最优解，而在25代之后，混合法的局部搜索能力逐渐增强，能够在全局最优解附近进行更精细地搜索，从而避免越过全局最优解。

根据粒子群算法，惯性权值线性递减法和混合惯性权值法的最优粒子位置分别为(78 188 208 214)和(95 152 186 212)所对应的节点号，评估函数最小值分别为5.97×10-2和4.29×10-2。

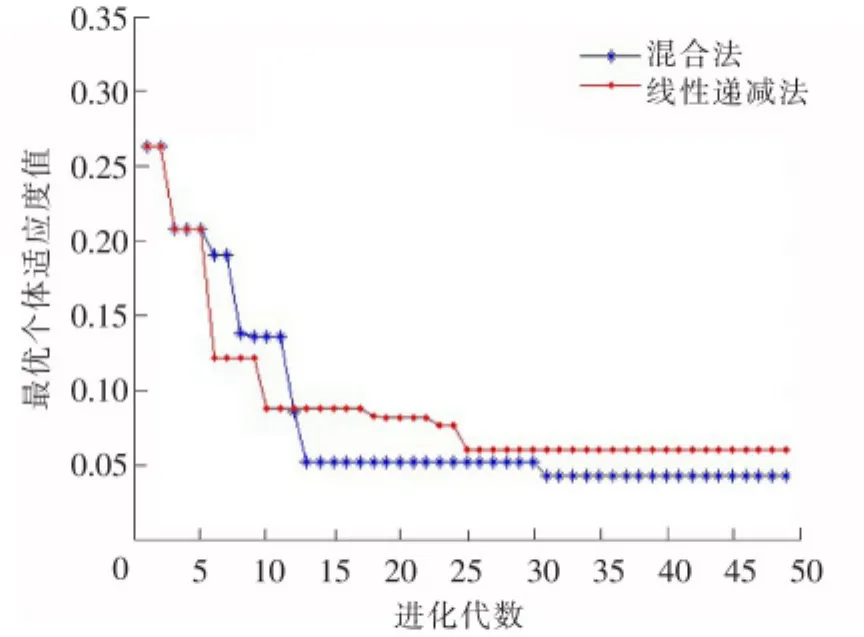
图3 适应度值曲线Fig.3 Curve of the fitness value

3 夹具设计实例

本文案例应用如图4、图5所示的某车身前翼子板，该零件作为遮盖车轮的车身外板，其装配质量直接影响到前轮转动及跳动时的最大极限空间，因此该零件的夹具定位策略分析非常重要。

图4 前翼子板Fig.4 Front fender

图5 前翼子板网格Fig.5 Mesh of the front fender

翼子板的定位策略应用“4-2-1”定位，第2、第3基准面上分别用2个、1个定位点来限制零件的刚体运动，主平面内的4个定位点由粒子群算法随机生成，经过优化得到最终主平面内定位点布局。对翼子板施加10倍重力作用，以使零件发生变形，粒子群编码方法与金属薄板零件编码方法相同。

为了能够比较分析，分别用本文所提出的惯性权值混合取值法和目前最常用的惯性权值线性递减法的优化结果做对比，各个参数设置均与薄板零件优化时相同。两种方法适应度值变化曲线如图6所示。

根据粒子群优化算法，混合取值法和线性递减法所得到的最优定位点位置分别为(15254 20380 8669 5095)和(3226 12272 11908 14965)，适应度函数最小值分别为1.001 483和1.243 852，粒子群算法惯性权值采用混合法取值时的优化结果要优于线性递减法，由图6及所得数据可以看出，在算法后期，本文所提出的混合法适应度值明显小于线性递减法，用混合法能够得到更优的定位方案。

经过优化后，翼子板应变分布情况如图7所示。

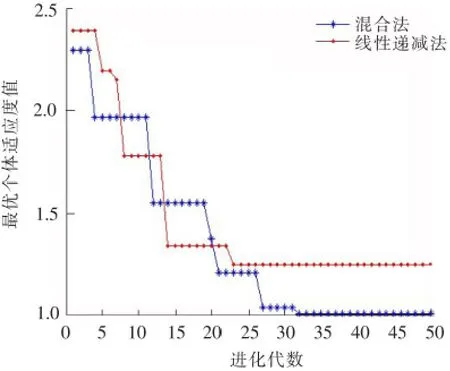
图6 适应度值曲线Fig.6 Curve of the fitness value

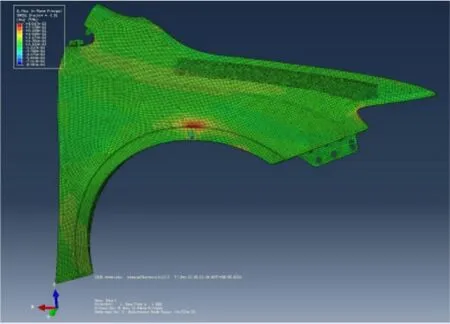
图7 应变分布图Fig.7 Distribution picture of the strain

4结语

本文提出一种基于改进粒子群算法的金属薄板零件定位策略优化方法，该方法通过改进惯性权值的取值方法，使算法在初期具有更强的全局搜索能力，在后期有更强的局部搜索能力，通过ABAQUS对金属薄板件进行了分析计算，并以某车型前翼子板为实例进行了验证，结果表明本文所提出的混合惯性权值法相对惯性权值线性递减法有更好的全局最优解搜索效果。然而本文所提出的改进算法只对惯性权值的取值方法进行了改进，还可综合考虑种群规模m、学习因子C等其他参数的取值对算法搜索能力的影响。本文以不同定位策略下零件的变形为目标函数，将来可将夹具装配偏差作为目标函数，进行夹具定位优化设计。

［1］ XIE S L，HSIEH CC.Clamping and welding sequence optimization forminimizing cycle time and assembly deformation［J］.International Journal Materials and Product Technology，2002，17(5/6):389-399.

［2］ CAIW，HU SJ，YUAN JX.Deformable sheetmetal fixturing:Principles，algorithms，and simulations［J］.JournalofManufacturing Science and Engineering-Transactions of the ASME，1996，118(3):318-324.

［3］ CAMELIO J，HU SJ，CEGLAREK D.Impactof fixture design on sheetmetal assembly variation［J］.Journal ofManufacturing Systems，2004，23(3):182-193.

［4］ LIBW，LAU K J.Robust fixture configuration design for sheetmetalassemblywith laserwelding［J］.Journal ofManufacturing Science and Engineering，2003，125(1):120-127.

［5］ CARLSON JS，SDERBERGR.Quadratic sensitivity analysisof fixturesand locating schemes for rigid parts［J］.Journal ofManufacturing Science and Engineering，2001，123(3):462-472.

［6］ VISHNUPRIYAN SC，RAMACHANDRAN K P.Optimization ofmachining fixture layout for tolerance requirements under the influence of locating errors［J］.International Journal of Engineering Science and Technology，2010，2(1):152-162.

［7］ XING Yanfeng，WANG Yansong.Fixture layout design based on two-stagemethod for sheetmetal components［J］.Proceedings of the Institution of Mechanical Engineers Part B-Journal of Engineering Manufacture，2013，227(B1):162-172.

［8］ 邢彦锋，赵晓昱，吴伟蔚.基于夹具配置的薄板件装配偏差分析模型［J］.计算机集成制造系统，2010，16(2):280-286.

XING Yanfeng，ZHAOXiaoyu，WUWeiwei.Assembly variation analysismodel based on fixture configurations for sheetmetal parts［J］.Computer Integrated Manufacturing Systems，2010，16(2):280-286.

［9］ 于奎刚，金隼，来新民.基于Taguchi的柔性薄板装配夹具稳健设计［J］.上海交通大学学报，2009，43(12):1941-1945.

YU Kuigang，JIN Sun，LAIXinmin.A fixture locating robust design method of compliant sheetmetal assembly based on Taguchimethod［J］.Journal of Shanghai Jiaotong University，2009，43(12):1941-1945.

［10］来新民，陈关龙，林忠钦，等.薄板冲压件焊装夹具设计方法［J］.机械科学与技术，2000，19(5):785-787.

LAIXinmin，CHEN Guanlong，LIN Zhongqin，et al.On fixture design of sheet stamping assembly［J］.Mechanical Science and Technology，2000，19(5):785-787.

［11］姜昂，范清林，郑丞，等.夹具定位方案稳定性评价及定位点搜索算法［J］.上海交通大学学报，2010，44(4):484-488.

JIANG Ang，FAN Qinglin，ZHENG Cheng，et al.Stability evaluation of fixture locating layout and research in locator-searching algorithm［J］.Journal of Shanghai Jiaotong University，2010，44(4):484-488.

［12］于颖，李永生，於孝春.粒子群算法在工程优化设计中的应用［J］.机械工程学报，2008，44(12):226-231.

YU Ying，LIYongsheng，WU Xiaochun.Application of particle swarm optimization in the engineering optimization design［J］.Chinese Journal of Mechanical Engineering，2008，44(12):226-231.

［13］郭文忠，陈国龙.离散粒子群优化算法及其应用［M］.北京:清华大学出版社，2012.

GUOWenzhong，CHEN Guolong.Discrete Particle Swarm Optimization Method and Its Application［M］.Beijing:Tsinghua University Press，2012.

［14］史峰，王辉，郁磊，等.MATLAB智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011.

SHIFeng，WANGHui，YU Lei，etal.Analysisof Thirty Cases for MATLAB Intelligent Algorithm［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2011.

［15］田雨波.粒子群优化算法及电磁应用［M］.北京:科学出版社，2014.

TIAN Yubo.Particle Swarm Optimization Algorithm and Its Application in Electromagnetism［M］.Beijing:Science Press，2014.

［16］钱锋.粒子群算法及其工业应用［M］.北京:科学出版社，2013.

QIAN Feng.Particle Swarm Optimization Algorithm and Its Industrial Application［M］.Beijing:Science Press，2013.

［17］纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京:科学出版社，2009.

JIZhen，LIAO Huilian，WU Qinghua.Particle Swarm Optimization Algorithm and Its Application［M］.Beijing:Science Press，2009.

［18］刘志雄，梁华.粒子群算法中随机数参数的设置与实验分析［J］.控制理论与应用，2010，27(11):1489-1496.

LIU Zhixiong，LIANG Hua.Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm［J］.Control Theory＆ Applications，2010，27(11):1489-1496.

［19］王杰文，李赫男.粒子群优化算法综述［J］.现代计算机(专业版)，2009(2):22-27.

WANG Jiewen，LIHenan.Summary of particle swarm optimization algorithm［J］.Modern Computer，2009(2):22-27.

［20］任斌，丰镇平.改进遗传算法与粒子群优化算法及其对比分析［J］.南京师范大学学报(工程技术版)，2002，2(2):14-20.

REN Bin，FENG Zhenping.Improved genetic algorithm and particle swarm optimization aswell as comparison between them［J］.Journal of Nanjing Normal University(Engineering and Technology Edition)，2002，2(2):14-20.

［21］张丹，韩胜菊，李建，等.基于改进粒子群算法的BP算法的研究［J］.计算机仿真，2011，28(2):147-150.

ZHANG Dan，HAN Shengju，LI Jian，et al.BP algorithm based on improved particle swarm optimization［J］.Computer Simulation，2011，28(2):147-150.

［22］孙磊，贾云献，王卫国，等.基于粒子群优化核独立分量的特征降维算法及其应用研究［J］.河北科技大学学报，2013，34(1):60-66.

SUN Lei，JIA Yunxian，WANGWeiguo，et al.Feature dimension reduction of kernel independent component by particle swarm optimization and its application［J］.Journal of Hebei University of Science and Technology，2013，34(1):60-66.

Optimization of sheet components locating scheme based on improved particle swarm optimization

ZHANG Heng，XING Yanfeng
(Automotive Engineering College，Shanghai University of Engineering Science，Shanghai201620，China)

The current sheet components locating scheme optimization needs a great deal of finite element analysis，which limits the fixture design efficiency.To reduce finite element analysis times，this paper proposes amodified particle swarm optimization algorithm based on the inertia weight，and through the secondary developmentof finite elementsoftware，the improved particle swarm optimization is applied to fixture locating scheme design.Taking the front fender of some vehicle as the living example，the fixture locating scheme is optimally designed，which proves themethod effective.

vehicle engineering;sheetmetal component;particle swarm optimization;fixture locating scheme algorithm

TP391

A

1008-1542(2015)03-0300-06

10.7535/hbkd.2015yx03012

2014-10-15;

2014-12-15;责任编辑:冯 民

国家自然科学基金(51105241)

张 恒(1989—)，男，河北辛集人，硕士研究生，主要从事薄板件定位策略优化方面的研究。

邢彦锋副教授。E-mail:xyf2001721@163.com