Banach空间中线性算子的广义Drazin逆的几种新特性

林梅羽

(莆田学院 基础教育学院，福建 莆田 351100)

Banach空间中线性算子的广义Drazin逆的几种新特性

林梅羽

(莆田学院 基础教育学院，福建 莆田 351100)

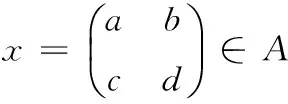
Banach空间；舒尔补；Drazin逆；分块矩阵

1958年，美国数学家M.P.Drazin利用R.Penrose定义了广义逆，并在研究结合环的代数结构中还定义了一种伪逆，这里所说的伪逆即为后来被大家广泛称为的Drazin广义逆.1976年，Campbell、Meyer 和Rose[1]对矩阵的Drazin广义逆的连续性做了大量的研究并讨论了方阵的Drazin逆在奇异系数线性微分方程中的一些应用.从此以后，众多学者们开始研究矩阵的Drazin广义逆，于是使得矩阵的Drazin广义逆得到了空前的发展.1979年，Campbell[2]讨论了方阵的Drazin逆在奇异常系数矩阵差分方程中的应用，得出了一系列的结论，同时提出了一种特殊分块矩阵的Drazin逆的表达式的open问题，遗憾的是该问题至今仍未得到解决.

1 几个引理

设A是幺元为1的B代数，且a∈A.记σ(a)、r(a)和ρ(a)分别为a的谱、谱半径和分解集合.记A-1为B代数A的可逆元素集，A0为B代数A的幂零元素集，A00为B代数A的拟幂零元素集.

如果存在元素b∈A满足：bab=b,ab=ba,a-a2b∈A00，则称b是a的广义Drazin逆，且b是唯一的，记作b=ad.

显然，当a-a2b∈A0时，广义Drazin逆即为Drazin逆，也就是说Drazin逆是广义Drazin逆的一种特殊情况.当a-a2b∈A0换成a=aba时,Drazin逆即为群逆，也就是说群逆是Drazin逆的一种特殊情况，这里记a#为a的群逆.

如果存在元素p=p2∈A满足：a+p∈A-1，ap=pa∈A00，则称p是a的谱幂等元，且p是唯一的，记作p=aπ.

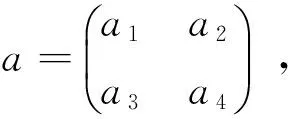
再给出本文的几个重要的新特性之前，先给出几个即将用到的重要引理.

引理1 设A是幺元为1的B代数，p是A幂等元.如果x∈pAp，那么

证明详细参见参考文献[9].

引理2 设b,q∈A00，且qb=0.则b+q∈A00.

证明详细参见参考文献[9,10].

引理3 设b∈Ad，a∈A00.

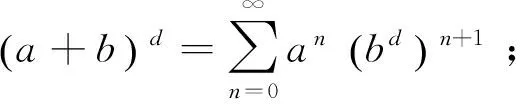
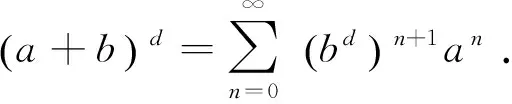
证明详细参见参考文献[9].

和

证明 由广义Drazin逆的定义可知：

于是

又

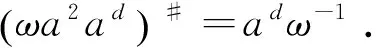
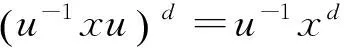
证明 由x∈Ad可得，存在a∈A满足：xax=x，ax=xa，a-a2x∈A00.于是，

则u-1xu∈Ad.又

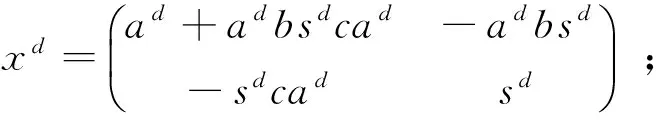
在满足远景新增110 MW负荷需求及单台机组或柔直单极的备用容量情况下，从投资费用F最低的角度出发，建立考虑1回80 MW容量的柔直和天然气供电方案的整数规划模型如下：

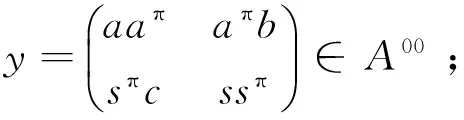
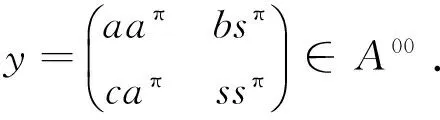
证明 首先证明(1)和(2)等价.

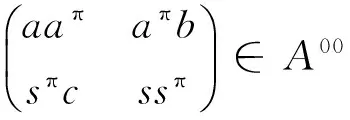
由aπbsd=adbsπ和sπcad=sdcaπ易知：aπbsdcad=adbsπcaπ.

于是再次利用矩阵乘法运算验证可知：

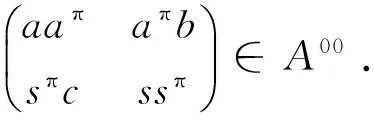
最后证明(2)和(3)等价.

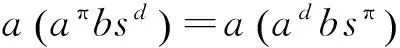
aaπbsd=0和aπbsds=0.

从而bsds=aadbsds=aadb，则

aπb=b-aadb=b-bsds=bsπ.

反之，由aπb=bsπ可知：aπbsd=adbsπ.

同理可证sπcad=sdcaπ等价于sπc=caπ.

因此，(2)和(3)等价.

2 广义Drazin逆的几种新特性

caπbssd=0，aaπbssd=0，ssπc=0，aπbsπc=bsπcaad=0，

则a∈Ad，且

(1)

证明 由aπ+aad=p和sπ+sasπ=1-p可知：

利用矩阵乘法结合已知条件易知：yz=0.

首先证明y∈A00.

由引理1易知：y2∈A00.

容易验证y1y2=0，从而由引理2可知：y1+y2∈A00.

接着证明z∈Ad.

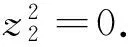
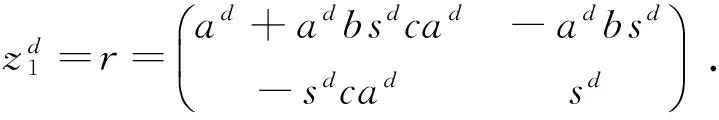
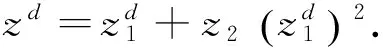
由引理3可知：x∈Ad且

从而

综上所述：

根据定理1中的(1)式很容易得到如下推论，下面给出的推论1即为文献[8]中定理2.5的推广形式.

(2)

如果假设定理1中的广义舒尔补是可逆的，则易知sπ=0且得到下面的推论2，该推论即为文献[9]中定理3.1的推广形式.

(3)

下面给出不同条件的结论，其证明过程类似上面方法，在此不再给出详细证明，感兴趣的读者不妨可以试着推导一下.

aaπ-aπbsdcaπ=0，sπcaπ=0，caπb=0，aπbsπ=0，ssπc=0=bssπ，

则x∈Ad，且

(4)

(5)

(6)

3 结束语

[1]SLCampbell,CDMeyer,NJRose.ApplicationoftheDrazininversetolinearsystemofdifferentialequationswithsingularconstantcoefficients[J].SIAMJApplMath,1976,31:411-425.

[2]SLCampbell,CDMeyer.GeneralizedInverseofLinearTransformations[M].London：Pitman,1979.

[3]XChen,RobertE,Hartwig.Thegroupinverseofatriangularmatrix[J].LinearAlgebraAppl,1996,237:97-108.

[4]JMiao.ResultsofDrazininverseofa2X2blockmatrices[J].JShanghaiNormalUniversity,1989,18:25-31.

[5] 董鹏飞.Schur补为零的分块矩阵Drazin逆表示[D].哈尔滨：哈尔滨工程大学，2011.

[6] 郭美华,刘丁酉.分块2次幂零矩阵的广义Schur补[J].武汉大学学报，2015,31(3):633-637.

[7] 卜长江,王光辉,宋晓翠.广义Schur补可逆的一些分块矩阵的Drazin逆表示[D].哈尔滨：哈尔滨工程大学，2012.

[8] 朱永林.分块幂等矩阵中广义Schur补的幂等性[J].数学实践与认识,2014,44(6):295-298.

[9]NCastro-Gonzalez,MFMartinez-Serrano.DrazininverseofpartitionedmatricesintermsodBanachiewicz-Schurforms[J].LinearAlgebraAppl，2010,432:1691-1702.

[10]CUIRunqing,LIXinglan,GAOJingli.ThedrazininverseofAmodifiedmatrixA-CB[J].JofMath,2014,34(1):12-16.

Several representations of the Drazin inverse of the linear operator in a Banach space

LIN Meiyu

(SchoolofBasicEducation,PutianUniversity,PutianFujian351100,China)

(责任编辑：张冬冬)

2015-10-13

林梅羽(1959-),男，福建莆田人，莆田学院基础教育学院高级讲师.

O177.2

A

1008-2441(2015)06-0012-06