波流数值水池模拟研究

吴梓鑫，朱仁庆，缪志刚，刘 珍，顾思琪

(江苏科技大学船舶与海洋工程学院，江苏镇江212003)

在复杂的海洋环境中，波浪与水流通常是共同存在的.潮流、洋流、河口处径流以及与波浪破碎有关的沿岸流、裂流及其所形成的近岸环流等水流会与波浪产生相互作用，使波幅、波高、周期等波浪要素发生变化，并使波浪发生折射甚至破碎.因此，研究波流的相互作用是开发海洋需要解决的关键问题，受到了国内外科研人员的重视.1911年，Rayleigh发现在潮汐中存在着波流的相互作用.文献［1-3］中通过实验研究了水流对波浪要素的影响;文献［4-5］中在数值理论方面做出了一定的贡献.但是，波流相互作用是极其复杂的非线性问题，其流动机理和作用特性仍需深入研究.随着计算机技术的成熟，数值水池已具备了信息量丰富、计算结果精确的特点，加上其成本低、改变条件方便、重复性好等优势，数值水池已经成为国际上研究海洋波浪问题的热门方法.目前，众多学者已经通过推板造波［6］、源项造波［7］、速度入口［8］等数值方法模拟出理想波浪.然而针对波流相互影响的研究还很少，此外，波浪与剪切流作用的数值模拟更是被很多人忽视.文中基于软件平台FLUENT二次开发构造二维数值波流水池，采用速度入口造波技术，不可压缩粘性流体Navier-Stokes方程为控制方程，通过流体体积法(volume of fluid，VOF)追踪自由液面，采用阻尼消波法在水池后方进行消波处理，成功模拟了波浪与均匀流及与剪切流共同作用的数值水池，并分析了水流对波浪的影响.

1 数学模型

1.1 控制方程

1)连续性方程:质量守恒方程

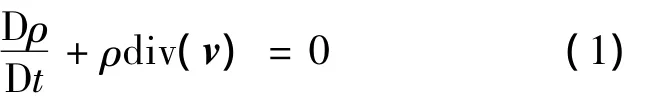
对于不可压缩流体，式(1)简化为:

式中:ρ为流体密度;v为流场速度矢量.

2)N-S方程:动量守恒方程

假设流体粘性系数为常数，则不可压缩流体的

运动方程，即N-S方程为:

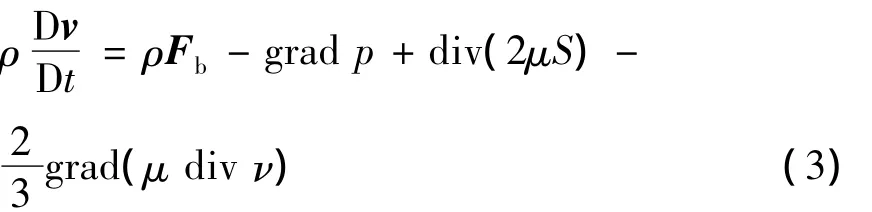
式中:μ为动力粘性系数;Fb为体力;p为压强;S为应变率张量.式(3)左端为单位体积流体的惯性力;右端第1项为单位体积的质量力;第2项为作用于单位体积流体的压强梯度力;第3项为粘性变形应力;第4项为粘性体膨胀应力.

对于不可压缩流体，N-S方程简化为:

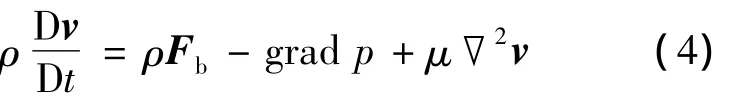
1.2 边界条件及自由液面追踪方法

数值水池底部法向速度为零，即:

文中采用VOF法追踪气液交界面.定义体积分数函数αq为单元内第q相流体所占有全部的体积与单元总体积之间的比.若αq=0，表明该单元内全部为空气;若αq=1，则表明该单元内都为液体;若0＜αq＜1，即为交界面.

每个控制体中，两相的体积分数之和为1，即:

两相之间的流体界面通过求解体积分数连续性方程来追踪，第q相流体的体积分数满足连续性方程:

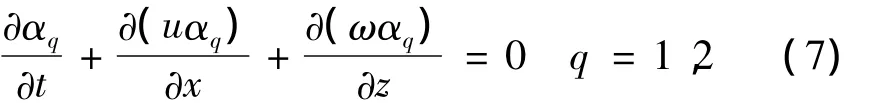
1.3 线性小振幅波理论

线性波又称Airy波，对于无限水深平面线性波，其解为:

波面方程:

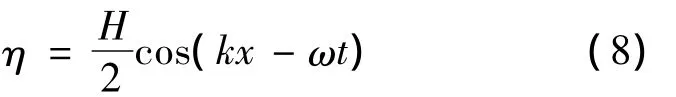
速度势:

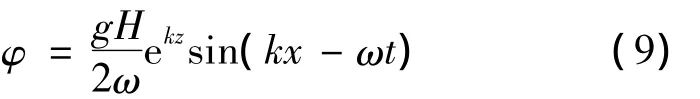
x方向速度:

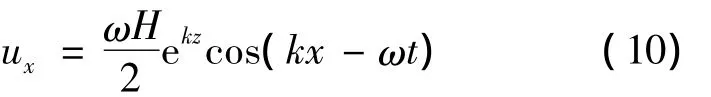
z方向速度:

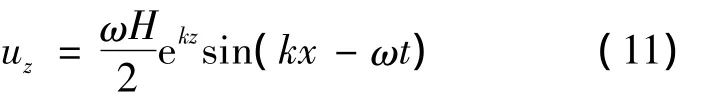
式中:H为波高;k=2π/λ;ω =2π/T;λ为波长;T为波浪周期;z为垂向坐标(向上为正);z=0为静水面.

1.4 消波理论

物理水池中，波浪传播到另一端池壁，将会产生反射，因而需在水池末端设置消波装置以消除反射波.对于数值水池，同样需要在水池的后部进行消波处理.数值消波主要有阻尼消波法和多孔介质消波法，这里采用阻尼消波法.

消波区内，动量方程(二维)为:

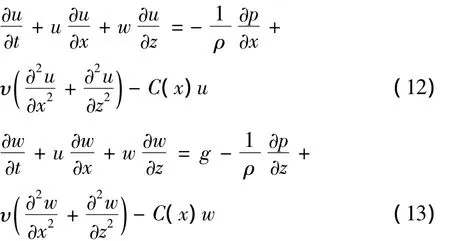
式中:C(x)为消波系数;υ为运动粘性系数.

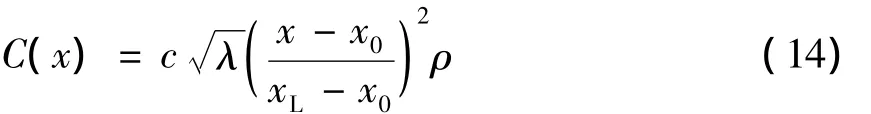
式中:c为系数，不同的数值水池其值不同，根据经验及试算，算例中c取10;λ为波长;x0，xL分别为消波区左、右边界的x坐标值;ρ为流体密度.

2 波流数值水池模拟

2.1 建模与网格划分

采用ANSYS 14.5中GEOMETRY模块建模.数值水池尺寸为30 m×5 m，水深3 m，水面以上为空气，水池后部10 m为消波区.用MESH模块划分网格，在波长方向上，单位网格长度为波长的1/100;在水深方向，为了更精确地捕捉到自由液面，在静水面上下一个波高内加密网格，网格高度为波高的1/60，在远离自由液面处网格渐疏.模型及网格划分情况如图1，2所示.

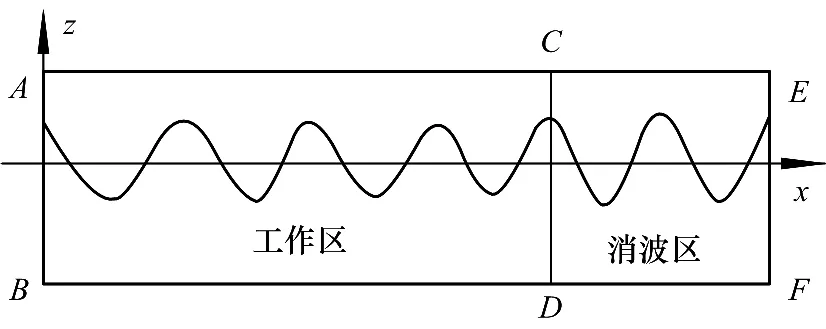
图1 数值水池Fig.1 Schematic diagram of the numerical tank

图2 网格划分Fig.2 Schematic diagram of the grid

2.2 边界条件及计算参数设置

水池左端AB设置为速度入口(velocity-inlet)，上方边界AE为压力入口(pressure-inlet)，底部BF为固壁(wall)，右端EF为压力出口(pressure-outlet)，区域CEFD为消波区.

采用FLUENT中二维非定常分离隐式求解器求解，压力方程选用加权体积力格式(body force weighted)，压力速度耦合方式采用PISO算法，体积分数方法为几何重构(geo-reconstruct)，压力参考值为一个标准大气压，重力加速度为-9.81m/s2，时间步长为0.005s.

2.3 波浪数值水池验算

为了验证波流数值水池的正确性，首先对具有如下波浪要素的余弦波进行了数值模拟.

表1 余弦波Table 1 Cosine wave

图3为波浪生成和传播过程示意图，上部分为空气，下部分为水.可以看出，在t=30s时，水池已形成稳定的波形.

图3 波浪的生成和传播过程Fig.3 Generation and propagation process of the wave

在数值波浪水池中x=1/5λ，λ(即x=5m)处设置波高仪以实时监测波高.图4为所监测波高仪随时间t变化时程曲线，蓝色为数值计算结果曲线，红色为理论曲线，可以得到其运动的周期为1.79s，与理论波形的周期基本吻合，波幅为0.148 m，与理论值误差为1.33%.

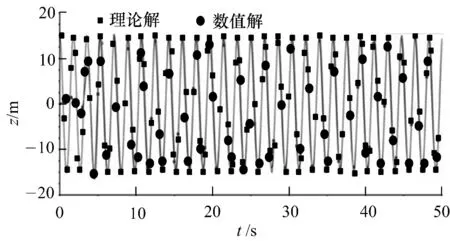
图4 自由液面坐标时程曲线Fig.4 Time curve of the surface

图5为消波区波形随时间走势图，从图中可以清晰看出波形衰减的过程，在水池最右端，波浪已基本完全消失，验证了文中所用阻尼消波的可行性.

图5 不同时刻消波区波形Fig.5 Waves′shape in the damping domain at different time

图6为数值水池在静水状态和波浪状态下的静压力云图.a)图显示的是静水状态的压力云图，图中压力状态呈分层分布，压力从上至下逐渐变大，且最大静压力的值与理论值相当.b)图展示的是波浪状态下的压力云图，可以看出波谷处的静水压力值小于波峰处的静水压力值.从而进一步通过静水和波浪两个状态分别验证了数值模拟波浪的正确性.

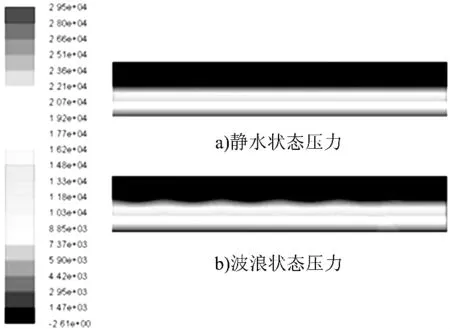
图6 静水压力云图Fig.6 Hydrostatic pressure contours

2.4 波浪与均匀流数值模拟及分析

目前，为兼顾准确性和工程需要，波浪和水流共同作用一般采取文献［9］中提出的波流共同作用的流速场理论，即波流水平速度叠加法，其速度关系如下:

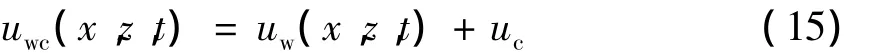
式中:uwc(x，z，t)为波流联合场水平速度;uw(x，z，t)为波浪场水平速度;uc为均匀流场水平速度.

文中对流速uc=uw/4，uc=uw/8和uc=-uw/8的3种工况波流水池进行数值模拟，分别命名为算例1，2，3，uw=2.79m/s.为保证波流数值水池与上述单独波浪水池结果的可比性，其几何模型、边界条件、物理属性、计算参数设置以及消波区域设置与单独波浪水池保持相同.

图7为算例0～3波长方向x=15 m处波高时程曲线，通过比较可看出，由于水流的作用，形成稳定波形所需时间发生了变化，当波流同向时，流体对波浪具有推动作用，其传播速度加快，形成稳定波形较单独波浪所需时间要短;反之，波流相向时，流体对波浪传播具有阻碍作用，波流场形成稳定波形则所需时间变长.

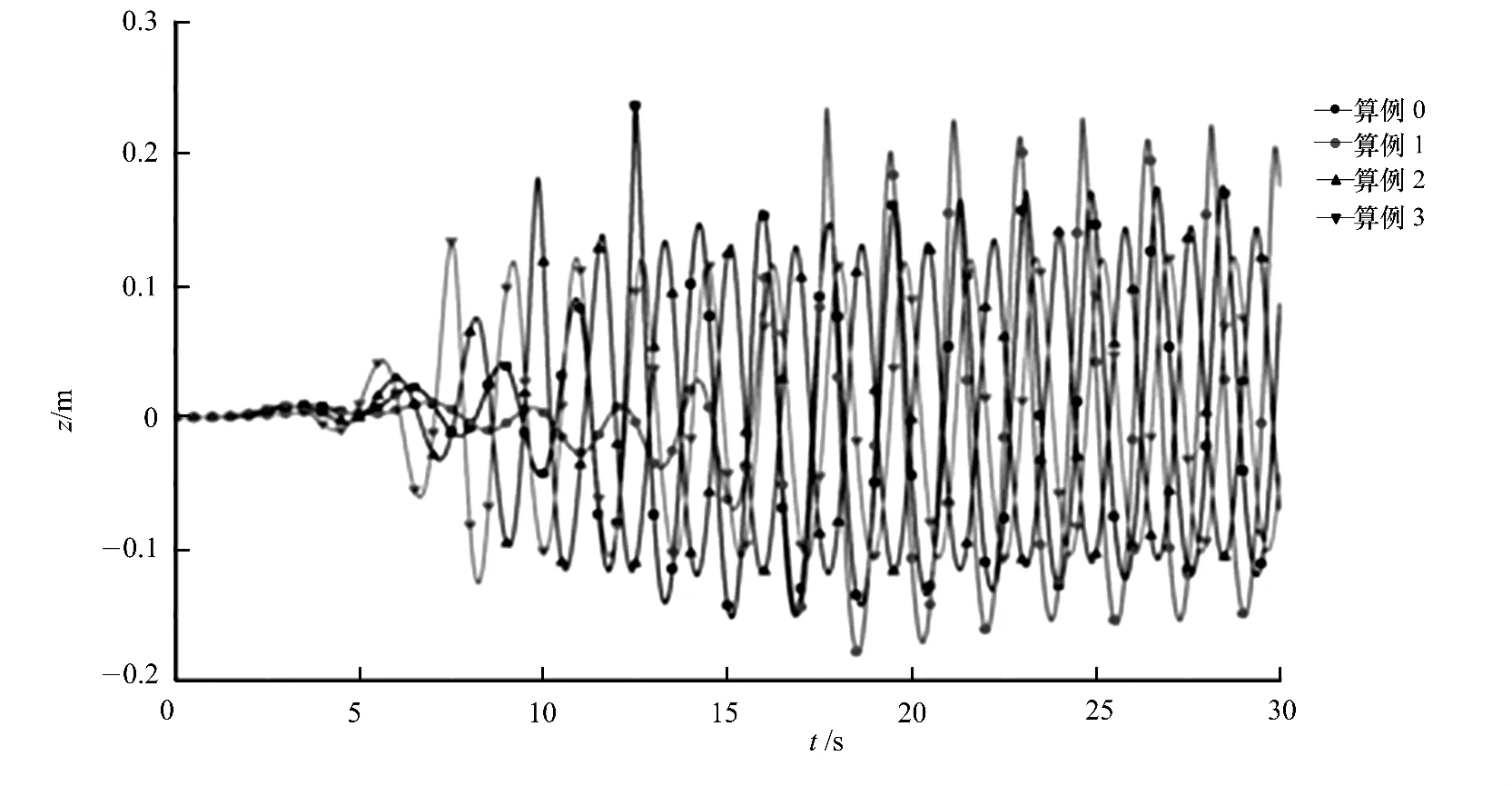
图7 x=15m处波幅时程曲线Fig.7 Time curve of the wave amplitude at x=15m

对于无限水深，设L为波流场波长;A为波流场波幅;L0为单独波浪场波长;A0为单独波浪场波幅，根据文献［10］，有

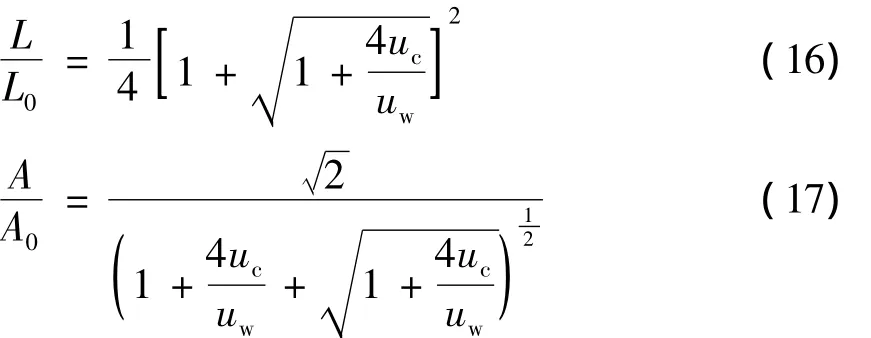
表2，3为波长和波幅计算结果分析表，数据显示数值模拟很好地验证了波流场中水流对波浪波长及波幅的影响.当波流同向时，由于波速增大，波形被拉长，波幅减小;反之，波流相向时，波速减小，波形变窄，波幅增加.图8为波长和波幅计算结果与理论值对比曲线，数值结果与理论结果基本吻合.

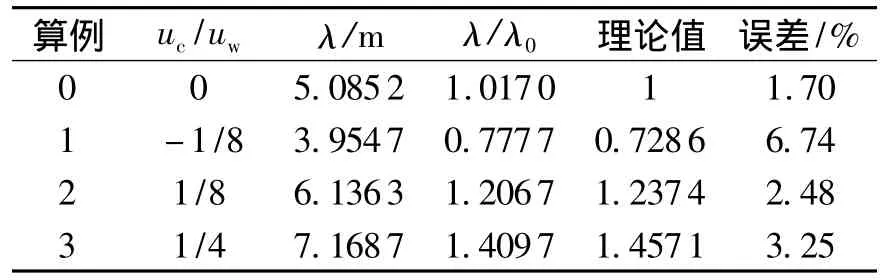
表2 波长计算结果Table 2 Calculation results of wavelength

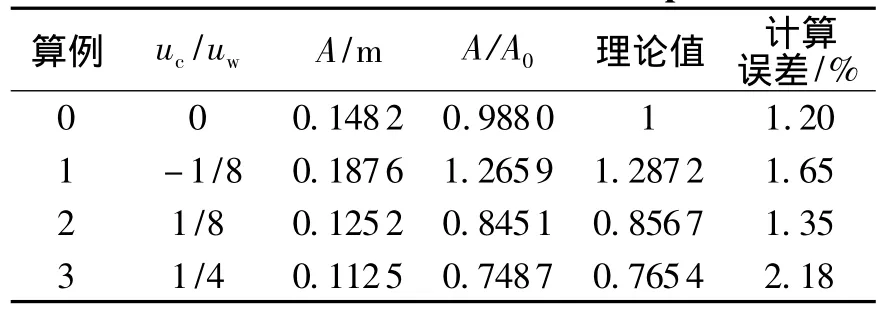
表3 波幅计算结果Table 3 Calculation results of amplitude

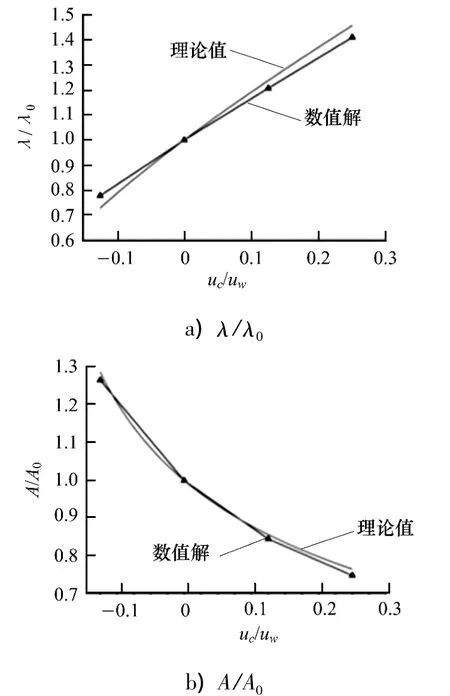
图8 计算结果与理论值对比曲线Fig.8 Contrast curve of the calculations and the theoretical values

2.5 波浪与剪切流联合作用数值模拟

在实际工程应用中，基本不存在完全的均匀流，海底河床等因素必然形成剪切流等非均匀流.文中对r=0.03，0.06，0.09和0.12的4种剪切率进行波浪与剪切流的数值模拟，分别记为算例4～7，水池几何模型、边界条件、物理属性、计算参数设置以及消波区域设置与单独波浪水池保持相同，在水深1.5m处，保持所加流速为波速的1/8，即uc=1/8uw.图9为t=50s时4种工况波形图，波长及波幅变化情况如表4所示.

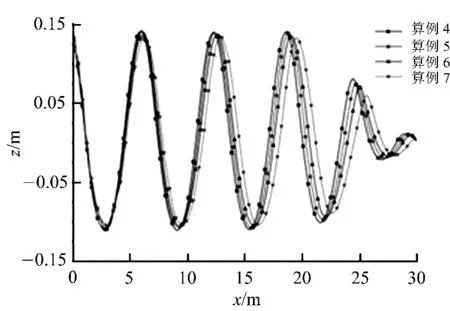
图9 t=50s时波形Fig.9 Waves′shape at t=50s

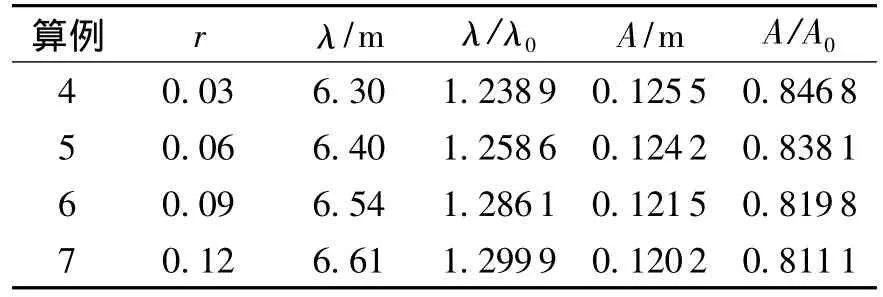
表4 波长、波幅计算结果Table 4 Calculation results of wavelength and amplitude

与单独波浪场相比，叠加剪切流后，由于流的作用，波浪波长增加了，波幅则减小，变化趋势与叠加均匀流一致.波长及波幅随剪切率变化曲线如图10所示，根据数值模拟结果，文中对波长和波幅进行函数拟合，结果如下:

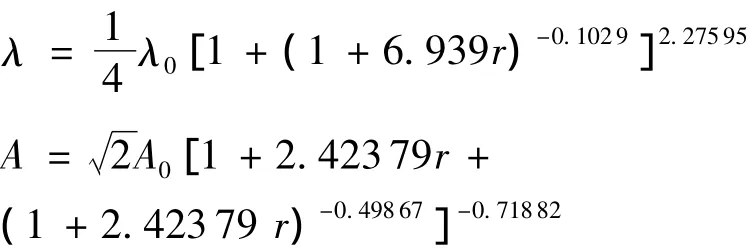
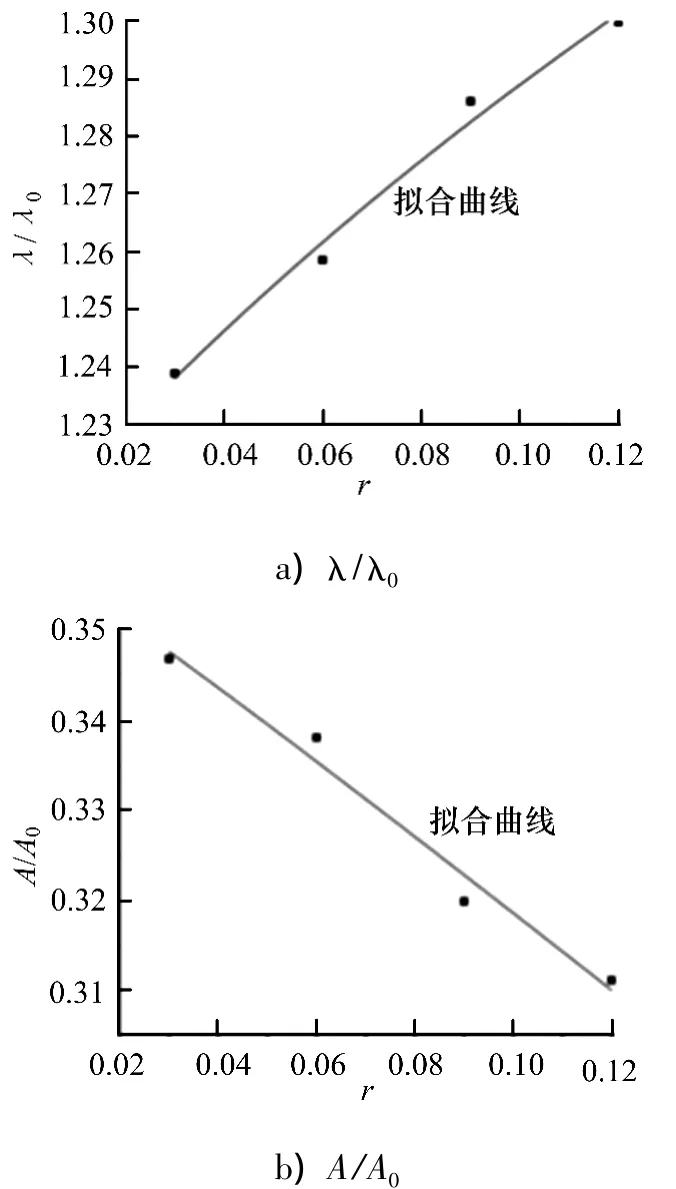
图10 λ/λ0及A/A0随剪切率变化曲线Fig.10 Curve of λ/λ0and A/A0changing with the rate

3 结论

以商业软件ANSYS中的FLUENT为平台，通过加载UDF程序进行二次开发实现速度入口造波，采用VOF方法追踪气液两项自由面，在水池后方动量方程中添加源项形成阻尼消波，成功建立了二维波浪、波流数值水池.

1)将设置造波边界法应用于FLUENT软件，成功模拟了效果良好的单独波浪以及波浪—均匀流和波浪—剪切流数值水池，验证了该造波方式和所用阻尼消波技术的可行性;

2)通过在入口处定义波流叠加的边界条件，模拟了波浪与不同流速联合作用的波浪—均匀流数值水池.表明波流同向时，水流对波浪传播具有推动作用，使波形变长，波幅减小;波流相向时，水流阻碍波浪传播，使波形变短，波幅增加，与理论结果基本吻合;

3)模拟了波浪与不同剪切率剪切流联合作用的波浪——剪切流数值水池，探究了剪切率对波流数值水池的影响，通过拟合，得到了波长及波幅与剪切率的函数关系，以便工程应用.

References)

［1］ Thomas G P.Wave-current interactions:an experimental and numerical study.part 1.linear waves［J］.Journal of Fluid Mechanics，1981，110:457 -474.

［2］ Kemp P H，Simons R R.The interaction between waves and a turbulent current:waves propagating against the current［J］.Journal of Fluid Mechanics，1983，130:73 -89.

［3］ Hughes B A，Stewart R W.Interaction between gravity waves and as hear flow［J］.Journal of Fluid Mechanics，1961，10:385 -402.

［4］ Longuet M S，Stewart R W.Changes in the form of short gravity waves on long waves and tidal currents［J］.Journal of Fluid Mechanics，1960，8:565 -583.

［5］ Grant W D，Madsen O S.Combined wave and current interaction with a rough bottom［J］.Journal of Geophysical Research，1979，84:1797 -1808.

［6］ 赵艳，朱仁庆，刘珍，等.三维数值波浪水池的构建和粘性影响研究［J］.舰船科学技术，2014，36(5):42-48.Zhao Yan，Zhu Renqing，Liu Zhen，et al.Simulation of 3D numerical wave tank and viscosity research［J］.Ship Science and Technology，2014，36(5):42 - 48.(in Chinese)

［7］ 杨锦凌，孙大鹏，吴浩，等.斜坡堤波浪爬高和越浪数值模拟［J］.海洋工程，2013，31(2):45-52.Yang Jinlin，Sun Dapen，Wu Hao，et al.Numerical simulation of wave run-up and overtopping on sloping seawall［J］.The Ocean Engineering，2013，31(2):45 -52.(in Chinese)

［8］ 刘莎莎，顾煜炯，惠万馨，等.基于边界造波法的波浪数值模拟［J］.可再生能源，2013，31(2):100-103.Liu Shasha，Gu Yujiong，Hui Wanxin，et al.Wave numerical simulation based on wave-generation method of defining inlet boundary conditions.［J］.Renewable Energy Resources，2013，31(2):100 -103.(in Chinese)

［9］ 李玉成.波浪与水流共同作用下的流速场［J］.海洋工程，1983，(4):12 -23.

［10］ 邹志利.水波理论及其应用［M］.北京:科学出版社，2005:472-482.