火箭炮两轴耦合位置伺服系统线性自抗扰控制

郑颖，马大为，姚建勇，胡健

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

火箭炮位置伺服系统运行时方位和俯仰两轴联动产生的耦合力矩分别作用在两轴负载端，考虑耦合作用产生的负载力矩给系统带来的影响是很有必要的，而以往火箭炮位置伺服系统极少考虑耦合效应，以研究单轴即单输入单输出系统控制策略为主，且基于电机模型设计控制器而忽略了驱动器对系统动态的影响，因此有必要研究两轴耦合作用下基于实际系统速度闭环的火箭炮位置伺服系统控制策略和控制性能。火箭炮发射时负载瞬态变化大，受不平衡力矩和燃气流冲击力矩等强干扰，导致方位和俯仰两轴振动，使得后续射弹精度降低。为抑制强干扰作用实现火箭炮快速响应和稳定性的控制要求，设计具有解耦性能且对未知动态具有鲁棒性的控制器成为研究的重要内容。

火箭炮单轴伺服系统控制策略［1-3］能有效提高方位轴或俯仰轴跟踪精度和抗干扰性能，但没有给出对两轴耦合系统的控制效果。文献［4］提出了一种多输入多输出系统的鲁棒控制方法但需要很大的计算量。文献［5］针对不确定多输入多输出飞行器模型设计了基于变结构控制的鲁棒反馈控制器，分析了具有输入扰动和系统不确定性的多输入多输出系统采用变结构控制时的稳定滑模和渐进稳定条件，但此控制方法计算量较大。文献［6］对两输入两输出双环时滞系统采用了自抗扰控制方法，将耦合作用视为外部扰动。自抗扰控制［7］能补偿双环耦合作用，在解耦方面控制性能优于PI 控制。文献［8］将输入延时多变量系统作为一类输入无延时的高阶系统，通过自抗扰控制方法实时补偿系统总扰动。该控制方法能使多变量系统具有鲁棒稳定性，满足性能指标，但需要调节的参数较多，参数整定较为不易。文献［9］基于自抗扰控制方法提出了一种动态扰动解耦控制策略，对多变量系统的内部动态和外部扰动进行估计和补偿，并给出了稳定性分析。文献［10］分析了线性自抗扰方法对一类具有未知动态和外部扰动的多输入多输出非线性系统的控制性能。提出的控制目标即瞬时输出和理想输出的误差小于给定约束值，并给出了线性自抗扰控制器满足控制目标的证明。对飞行控制系统的仿真结果表明了该控制器的有效性。

文献［11 - 12］提出的线性自抗扰控制器(LADRC)设计方法具有收敛速度快、精度高、鲁棒性强、抗干扰能力强、控制参数少、算法简单、易于工程实现［13-15］等优点。本文建立了火箭炮方位、俯仰两轴耦合系统模型，通过模型近似得到了两轴系统的2 阶近似模型，并以此设计线性扩张状态观测器估计系统总扰动，通过设计的控制器对系统给予扰动补偿，有效抑制了火箭炮燃气流冲击影响，达到了控制目标。

1 火箭炮两轴耦合伺服系统模型

1.1 火箭炮两轴转台转矩方程

火箭炮方位和俯仰两轴转台坐标关系变换如图1所示［16］。Oxyz 表示大地坐标系，Oxayaza表示方位系统坐标系，Oxpypzp表示俯仰系统坐标系。方位系统(包括俯仰系统)绕其转动轴Oza(Oz)逆时针转动角度γ，俯仰系统绕其转动轴Oyp逆时针旋转角度β.

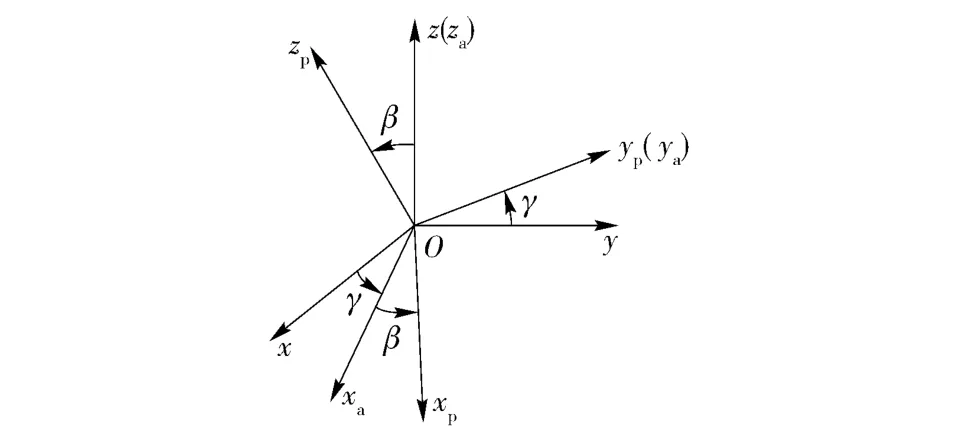
图1 两轴转台坐标关系变换图Fig.1 The coordinate relation diagram of the two-axis turntable

Ppa为俯仰系统坐标系Oxpypzp投影到方位系统坐标系Oxayaza的转移矩阵。由图1可得:

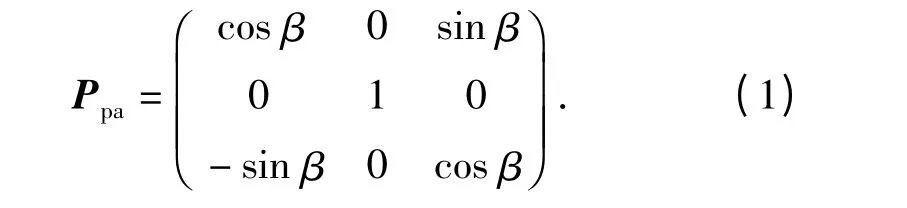
假设方位系统和俯仰系统相对于各自的坐标轴系是轴对称的，则方位和俯仰系统的转动惯量矩阵为

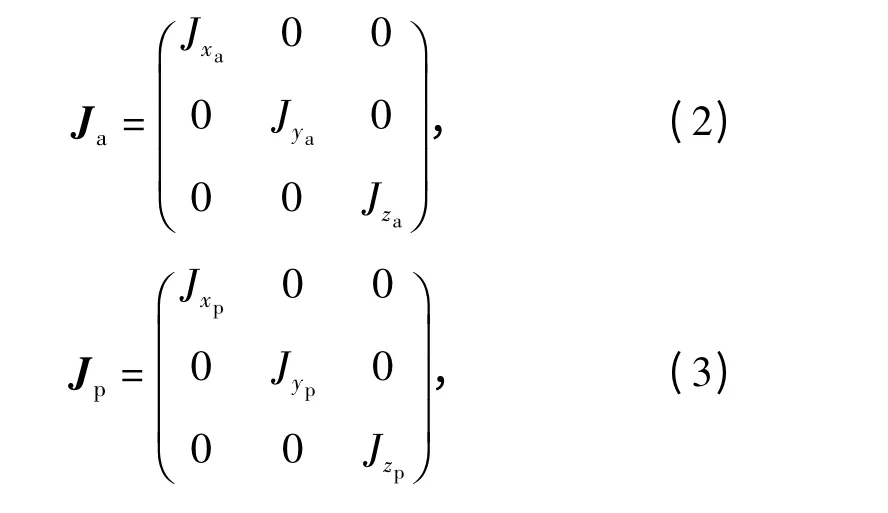
式中:Jxa、Jya、Jza分别表示方位系统绕Oxa、Oya、Oza轴的转动惯量;Jxp、Jyp、Jzp分别表示俯仰系统绕Oxp、Oyp、Ozp轴的转动惯量。

俯仰系统对方位系统坐标系Oxayaza的转动惯量矩阵为

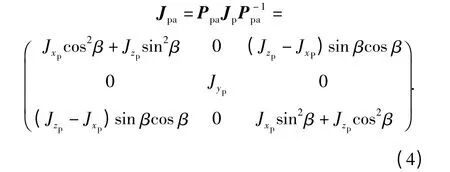
则俯仰系统相对于方位系统转动轴Oza的转动惯量为

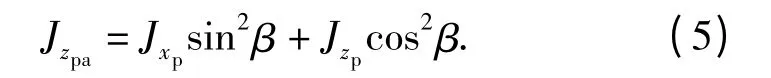
由于两轴联动方位系统相对于转动轴Oza的转动惯量耦合了俯仰系统相对于Oza的转动惯量。因此方位系统(包含俯仰系统)相对于方位系统转动轴Oza的转动惯量为

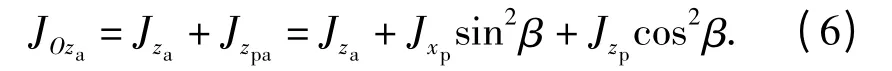
俯仰系统相对于转动轴Oyp的转动惯量为

定义方位系统转动时的角速度矢量为

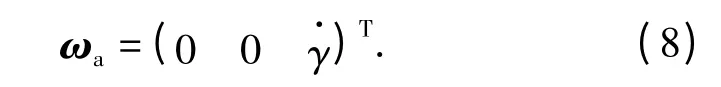
俯仰系统转动轴Oyp的角速度矢量为

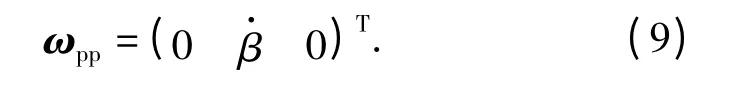
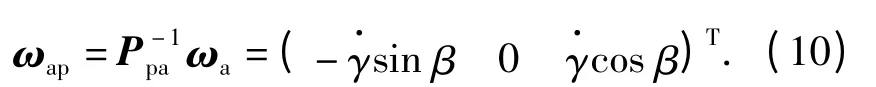
则俯仰系统角速度为

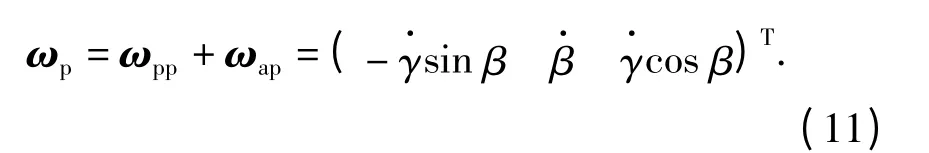
刚体的欧拉动力学方程为

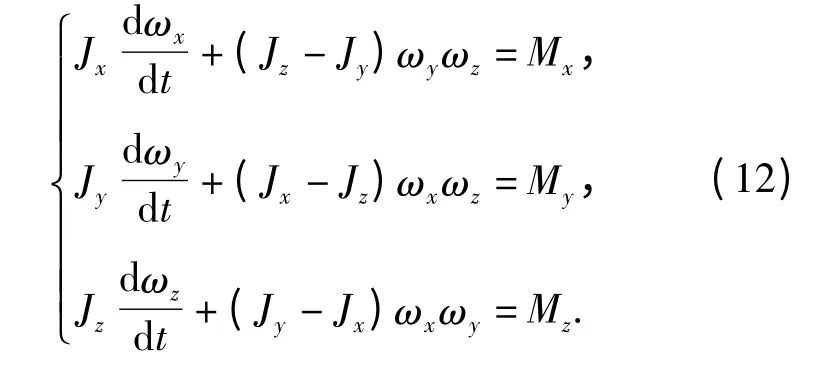
将(6)式、(7)式、(8)式和(11)式代入(12)式得两轴转台转矩方程为

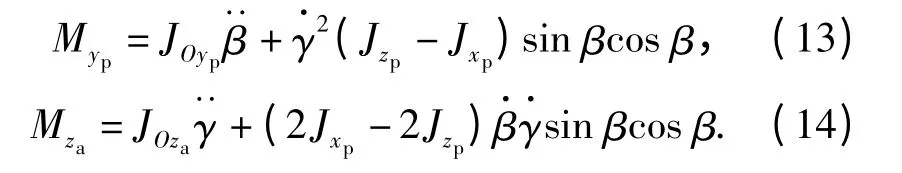
两轴系统相对各自坐标系的转动惯量如表1所示。

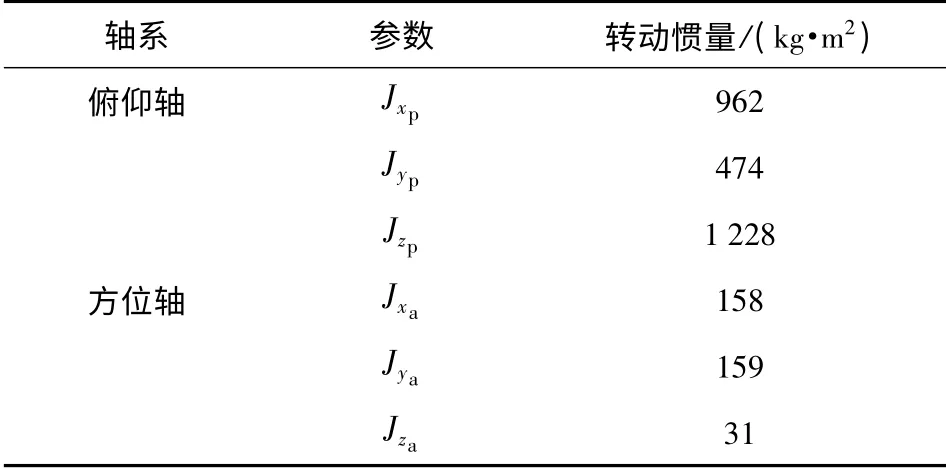
表1 两轴转台转动惯量Tab.1 Moment of inertia for two-axis turntable

将负载转矩折算到减速器前端即电机输出端，其中俯仰轴减速器减速比为ip=231，方位轴减速器减速比为ia= 192. 将表1中数据代入(13)式、(14)式，并折算到减速器前端，可得折算后的火箭炮伺服系统耦合力矩方程为

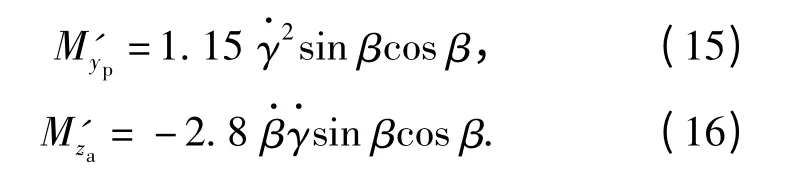
1.2 火箭炮两轴转台模型近似

建立火箭炮两轴转台速度环模型，通过频域分析建立系统近似模型从而进行控制器设计。火箭炮两轴耦合系统速度环模型如图2所示。

图2 火箭炮两轴耦合系统速度环模型Fig.2 Velocity loop model of rocket launcher servo system with two-axis coupling

图2中俯仰系统参数:Gpv(s)=15+20/s;Gpc(s)=10 +5/s，s 为拉普拉斯算子;电机电枢电感Lp=50 ×10-3H;电机电枢绕组电阻Rp=2.6 Ω;电机转矩系数KpT=1.11 N·m/A;折算到电机端的电机及负载转动惯量Jp=9.323 ×10-3kg·m2;粘滞摩擦系数Bp= 0.012 N·m·s/rad;电势系数KpE=0.64 V·s/rad;速度环稳态增益bp=0.073 rad/(s·V-1);Vp、Ip和Tp分别为电机电枢电压、电流和电磁转矩。

方位系统参数:Gav(s)=20 +25/s;Gac(s)=20 +15/s;La=33.5 ×10-3H;KaT=1.34 N·m/A;Ja=0.033 kg·m2;Ba=0.035 N·m·s/rad;Ra=1.32 Ω;KaE=0.78 V·s/rad;ba=0.073 rad/(s·V-1).

在Matlab/Simulink 中建立如图2所示的两轴耦合系统速度环仿真模型，通过频域分析得到火箭炮两轴耦合系统速度环模型Bode 图，并通过1 阶惯性环节近似系统速度环模型，如图3所示。

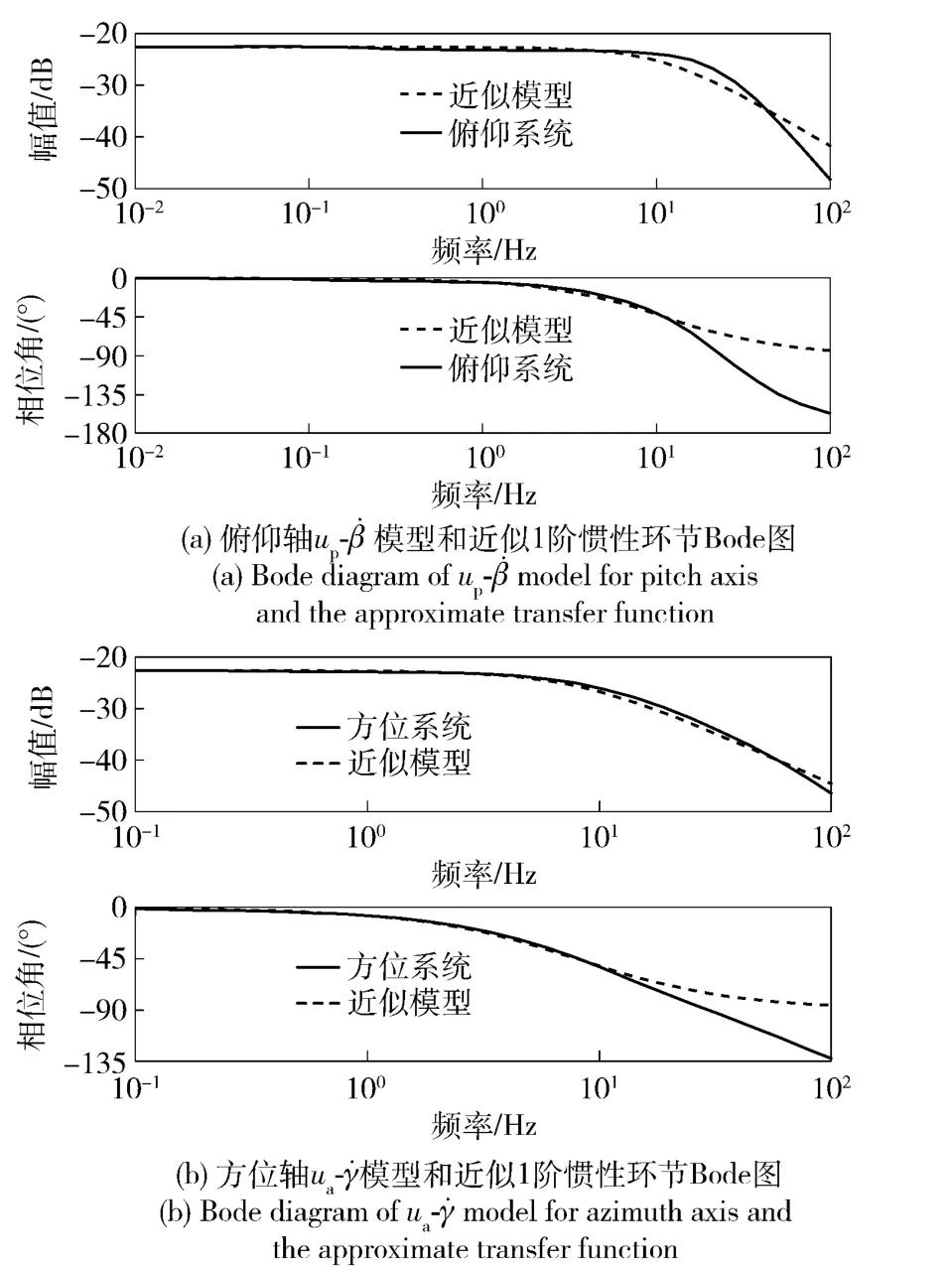
图3 方位和俯仰系统速度环模型及其近似模型Bode 图Fig.3 Bode diagrams of velocity loop models for azimuth and pitch axes and the approximate transfer functions

通过Bode 图频域分析可得俯仰轴和方位轴驱动器速度闭环模型在中低频段(如10 Hz 以内)，其幅频特性和相频特性均与1 阶惯性环节近似模型逼近，因此两轴模型均可由1 阶惯性环节近似，则俯仰轴和方位轴输入输出关系式分别为

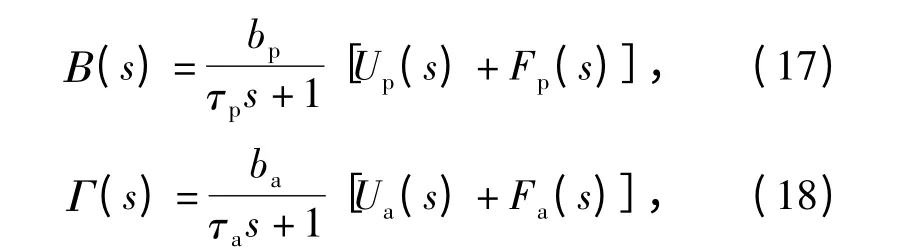
式中:τp、τa为两轴1 阶惯性环节近似模型的时间常数;B(s)、Г(s)为两轴输出角速度的频域表示;Up(s)、Ua(s)为两轴输入电压up、ua的频域表示;Fp(s)、Fa(s)为两轴模型近似误差fp(t)、fa(t)的频域表示。

由图3分析得俯仰系统参数ωnp为俯仰系统相位角φp(ω)= -45°时的系统转折频率，因此ωnp=70 rad/s，则τp=1/ωnp=1/70 s/rad. 同理可得方位系统参数τa=1/50.6 s/rad.

由(17)式和(18)式得火箭炮两轴系统扩张状态空间形式为

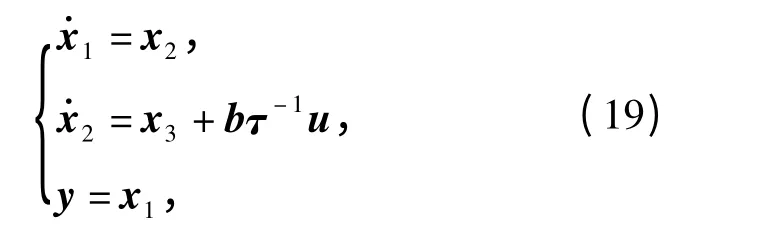
式中:x1=［xp1，xa1］T，为俯仰和方位两轴减速器输出端位置;x2为两轴减速器输出端角速度;x3为两轴系统扩张状态;b=diag(bp，ba)，为两轴速度环稳态增益;τ=diag(τp，τa);u=［up，ua］T.

2 火箭炮两轴耦合系统线性自抗扰控制

结合文献［11］中扩张状态观测器的设计方法和(19)式构建火箭炮两轴系统线性扩张状态观测器

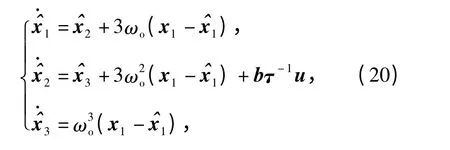
式中:ωo为两轴系统观测器带宽为俯仰和方位两轴减速器输出端角度估计;为两轴系统角速度估计;为两轴系统扩张状态估计。

设计的两轴系统自抗扰控制律为

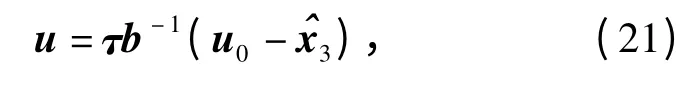
式中:u0=［up0，ua0］T，为两轴系统的误差反馈律。

系统扩张状态观测器的收敛性证明见文献［17］，线性扩张状态观测器误差随观测器带宽的增大而减小，当观测器带宽足够大时可使观测器误差趋于0，则所设计的状态观测器是收敛的。将(21)式代入(19)式，可得

由(22)式得通过控制律使原来的非线性系统变为线性积分器串联型系统，通过u0的设计使闭环系统具有满意的性能。

3 火箭炮两轴耦合系统仿真分析

取LADRC 中的u0为PID 控制律，其中up0=5 000 +100/s+100s，ua0=5 000 +80/s +100s，系统观测器带宽ωo=300 rad/s. 对火箭炮两轴耦合伺服系统进行仿真，俯仰轴给定位置输入信号r1=0.5 -0.5cos(2π×0.2t)，单位rad，即俯仰轴输入信号在0°～57.3°之间变化;方位轴位置参考信号r2=1 -cos(2π×0.2t)，单位rad，则方位轴输入信号在0° ～114.6°之间变化。

火箭炮伺服系统在发射时受燃气流冲击影响，负载干扰信号模拟燃气流冲击和负载转矩变化，负载转矩变化包括发射时火箭弹减少引起的转矩变化和(15)式、(16)式表示的两轴耦合力矩影响。给定火箭炮跟踪5 s 后每0.5 s 间隔发射一次，则俯仰轴和方位轴受负载干扰如图4所示。俯仰轴和方位轴驱动器的输入电压控制量up、ua如图5所示。由图5可得两轴驱动器输入电压满足-10 ～10 V 的输入范围。两轴耦合系统的角度跟踪误差曲线如图6所示。该LADRC 与传统PID 方法的控制效果比较如图7所示。

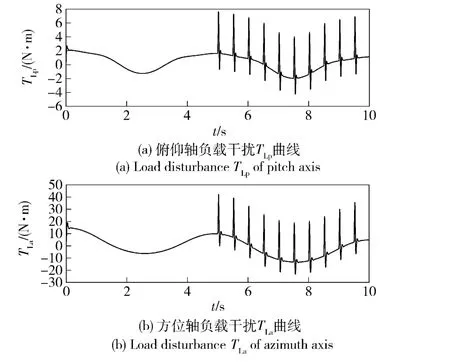
图4 俯仰轴和方位轴负载干扰曲线Fig.4 Load disturbance curves of pitch and azimuth axes

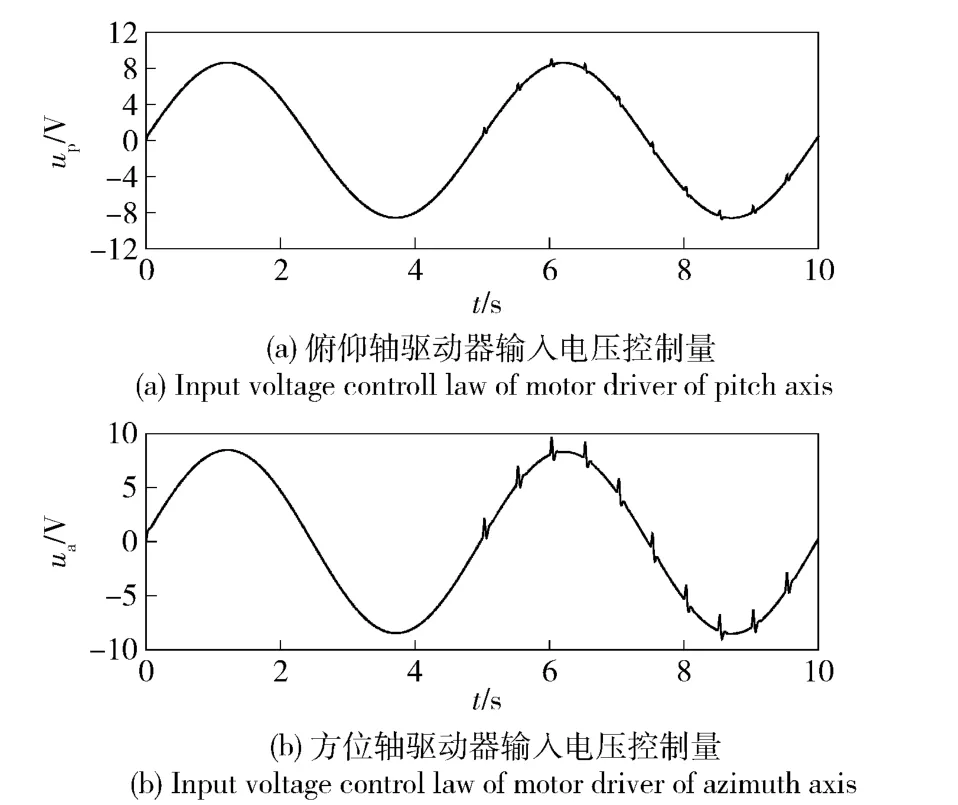
图5 俯仰轴和方位轴驱动器输入电压控制量Fig.5 Input voltage control laws of motor drivers of pitch and azimuth axes

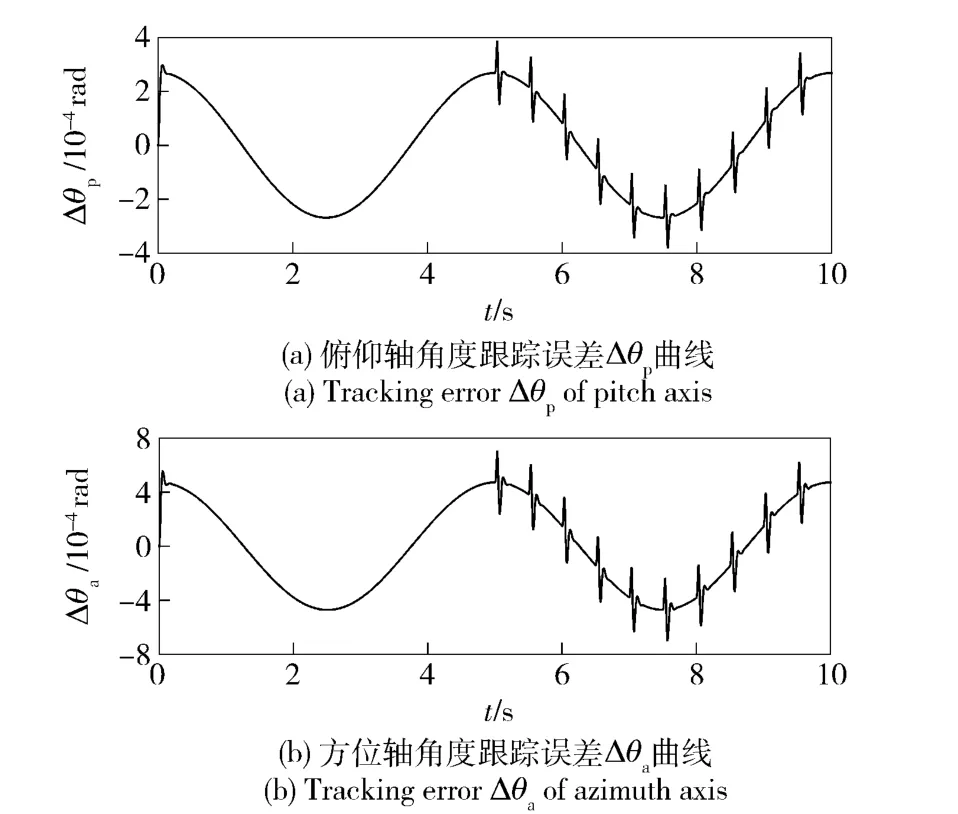
图6 俯仰轴和方位轴角度跟踪误差曲线Fig.6 Tracking error curves of pitch and azimuth axes

由图6得该自抗扰控制律使两轴耦合系统角度跟踪误差小于1 mil，满足控制精度要求，且响应速度快，在瞬态冲击下快速返回初始位置。由图7得该LADRC 精度远高于传统PID 控制，在燃气流持续瞬态冲击力矩和两轴耦合力矩影响下，传统PID控制的角度跟踪误差大于1 mil，不能满足控制需求，而提出的自抗扰控制律具有较高的跟踪精度和快速响应能力。

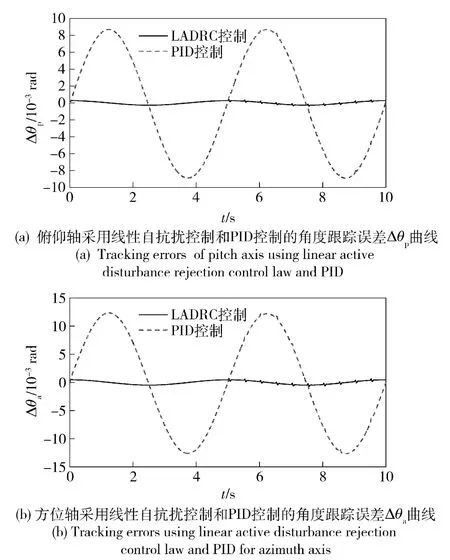
图7 耦合系统线性自抗扰和PID 控制的角度跟踪误差曲线Fig.7 Tracking errors of two-axis coupling system using linear active disturbance rejection control law and PID

4 实验分析

火箭炮伺服系统由上位工控机、基于DSP F2812 的位置控制器、方位及俯仰永磁同步电机、方位及俯仰驱动器、减速器和旋转变压器等组成。实验中将驱动器配置在速度环。为了模拟燃气流冲击给系统带来的影响，当系统进入稳态后，给系统施加一个持续8 s 的数值模拟信号，该冲击力矩通过DSP软件编程形成矩形波电压信号，将该电压施加给驱动器实现软件模拟冲击力矩。分别给俯仰和方位驱动器施加0.8 V 和1 V 的电压，通过文中所设计的线性扩张状态观测器对扰动进行补偿，伺服系统的输出位置曲线如图8所示。

由图8可得俯仰系统受到冲击后经过2 s 逐渐返回初始位置进入稳态，方位系统经过3 s 逐渐返回初始位置。当脉冲电压扰动信号阶跃变为0 V时，系统误差从0 变为负值，随后经过2.5 s 误差又趋于0. 图8表明通过扩张状态观测器估计的扩张状态对系统进行补偿能有效补偿冲击力矩对系统的扰动，提高系统的跟踪精度。

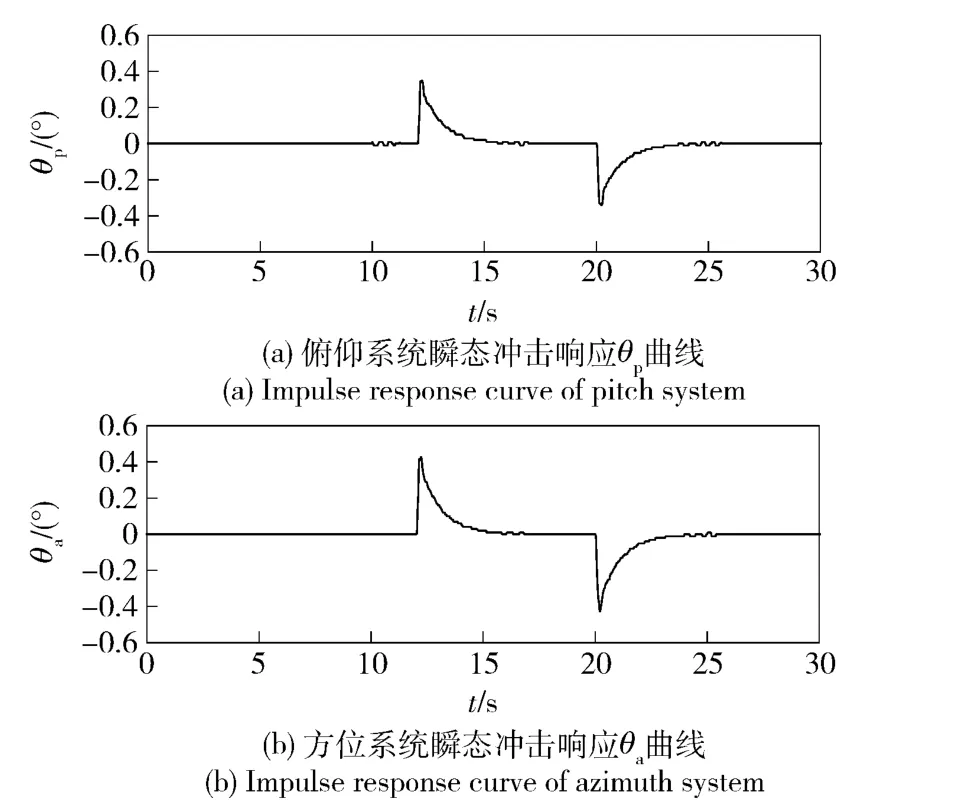
图8 系统瞬态冲击响应曲线Fig.8 Impulse response curves

5 结论

本文针对火箭炮位置伺服系统方位和俯仰两轴耦合的特点，建立了两轴系统耦合转矩方程并通过频域分析提出了两轴系统的2 阶近似模型。在此基础上设计了两轴线性扩张状态观测器和自抗扰控制律，对系统未建模干扰进行估计并实时补偿。仿真和实验结果表明所设计的控制器能有效补偿火箭炮发射时燃气流冲击力矩强干扰及系统耦合作用，提高了系统的跟踪精度，简化了控制器设计。

References)

［1］郭亚军，王晓峰，马大为，等. 自适应反演滑模控制在火箭炮交流伺服系统中的应用［J］. 兵工学报，2011，32(4):493 -497.GUO Ya-jun，WANG Xiao-feng，MA Da-wei，et al. Application of adaptive backstepping sliding mode control in alternative current servo system of rocket gun［J］. Acta Armamentarii，2011，32(4):493 -497. (in Chinese)

［2］陈福红，马大为，杨必武，等. 火箭炮交流伺服系统全局滑模控制［J］. 兵工学报，2012，33(6):641 -646.CHEN Fu-hong，MA Da-wei，YANG Bi-wu，et al. Global sliding mode control for rocket launcher AC servo system［J］. Acta Armamentarii，2012，33(6):641 -646. (in Chinese)

［3］吴跃飞，马大为，乐贵高. 控制受限的火箭炮位置伺服系统鲁棒自适应反步控制［J］. 兵工学报，2013，34(4):477 -483.WU Yue-fei，MA Da-wei，LE Gui-gao. Robust adaptive backstepping control for rocket launcher position servo system with constraint control［J］. Acta Armamentarii，2013，34(4):477 -483. (in Chinese)

［4］Perng M H，Lee T S. Nearly decoupled robust MIMO control systems design［J］. IEE Proceedings D:Control Theony and Applications，1992，139(1):53 -59.

［5］Jafarov E M，Tasaltin R . Robust sliding-mode control for the uncertain MIMO aircraft model F-18［J］. IEEE Transactions on Aerospace and Electronic Systems，2000，36(4):1127 -1141.

［6］Liu B，Xia Y Q，Chen J. Decoupling double-loop control system with ADRC［C］∥The 3rd International Conference on Innovative Computing Information and Control. Beijing:IEEE，2008:1016 -1025.

［7］Han J Q . From PID to active disturbance rejection control［J］.IEEE Transaction on Industrial Electronics，2009，56(3):900 -906.

［8］Xia Y，Shi P，Liu G P，et al. Active disturbance rejection control for uncertain multivariable systems with time-delay［J］. IET Control Theory Applications，2007，1(1):75 -81.

［9］Zheng Q，Chen Z Z，Gao Z Q. A practical approach to disturbance decoupling control［J］. Control Engineering Practice，2009，17(9):1016 -1025.

［10］Xue W C，Huang Y. On performance analysis of ADRC for a class of MIMO lower-triangular nonlinear uncertain systems［J］.ISA Transactions，2014，53(4):1 -8.

［11］Zheng Q，Gao L Q，Gao Z Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics［C］∥Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans:IEEE，2007:3501 -3506.

［12］Xue W C，Huang Y. On performance analysis of ADRC for nonlinear uncertain systems with unknown dynamics and discontinuous disturbances［C］∥Proceedings of the 32nd Chinese Control Conference. Xi’an:Technical Committee on Control Theory，Chinese Association of Automation，2013:1102 -1107.

［13］Zheng Q，Dong L L，Lee D H，et al. Active disturbance rejection control for MEMS Gyroscopes［J］. IEEE Transactions on Control Systems Technology，2009，17(6):1432 -1438.

［14］Zheng Q，Gao Z Q. On practical applications of active disturbance rejection control ［C］∥Proceedings of the 29th Chinese Control Conference. Beijing:Technical Committee on Control Theory，Chinese Association of Automation，2010:6095 -6100.

［15］Vincent J，Morris D，Usher N，et al. On active disturbance rejection based control design for superconducting RF cavities［J］.Nuclear Instruments and Methods in Physics Research A，2011，643(1):11 -16.

［16］赵建亚. 基于DSP 的转台伺服控制的设计与实现［D］. 哈尔滨:哈尔滨工业大学，2006.ZHAO Jian-ya. DSP-based design and implementation of servo control for table［D］. Harbin:Harbin Institute of Technology，2006. (in Chinese)

［17］郑颖，马大为，姚建勇，等. 火箭炮位置伺服系统自抗扰控制［J］. 兵工学报，2014，35(5):597 -603.ZHENG Ying，MA Da-wei，YAO Jian-yong，et al. Active disturbance rejection control for position servo system of rocket launcher［J］. Acta Armamentarii，2014，35(5):597 -603.(in Chinese)