双列角接触球轴承动刚度特性分析

邓四二，董晓，崔永存，胡广存

(1. 河南科技大学 机电工程学院，河南 洛阳471003;2. 慈兴集团有限公司，浙江 慈溪315301;3. 西北工业大学 机电工程学院，陕西 西安710071;4. 中航工业航空动力机械研究所，湖南 株洲412002)

0 引言

双列角接触球轴承由于具有较高的旋转精度、极限转速以及较大的刚性而广泛应用于武器装备、军用车辆等领域。随着对主机性能要求的不断提高，对与之配套的双列角接触球轴承性能的要求也越来越高。双列角接触球轴承动刚度是描述其动态性能的重要参数，提高动刚度对改善轴承支承特性，提高主机安全性与可靠性具有重要意义。

国内外学者已在滚动轴承刚度方面做出许多研究。Wan［1］基于赫兹接触理论提出了滚动轴承在简单负荷状态下变形和刚度的计算表达式。Bourdon等［2］建立刚度矩阵，分析了套圈变形对刚度的影响，得出角接触球轴承的预紧是影响其刚度的重要因素。Szuminski［3］分析了角接触球轴承的载荷分布，并在此基础上研究了轴承的瞬态刚度。Sarangi等［4，5］考虑了表面粗糙度以及润滑油粘度随压力变化的影响，求得了点接触轴承在等温弹流润滑条件下刚度的数值解。Gunduz 等［6］在单列轴承理论的基础上提出并验证了面对面、背靠背和串联布置的双列角接触球轴承的刚度矩阵。综观目前的研究，对双列角接触球轴承刚度计算［7-10］多为在静力学或拟静力学条件下的近似计算，且忽略了润滑油膜的影响，仅考虑滚动体与滚道之间的赫兹接触，将赫兹接触刚度近似当作轴承刚度，计算误差较大。轴承在实际工作中，滚动体与滚道之间形成的润滑油膜［11］对其动态性能影响很大，应予以考虑。加入对油膜刚度的考虑使轴承刚度模型更为完善，计算结果更加精确。

鉴于此，本文拟在双列角接触球轴承动力学分析基础上，建立双列角接触球轴承动刚度仿真分析模型，基于Fortran 编程软件及ADAMS 动力学仿真软件开发双列角接触球轴承动刚度仿真模块，分析轴承结构参数与工况参数对其动刚度的影响，为双列角接触球轴承的动刚度计算及优化设计提供理论依据。

1 双列角接触球轴承动刚度模型

滚动轴承刚度是指轴承套圈在负荷方向上产生单位相对弹性位移量所需的外加负荷［12］，可表示为

式中:Q 为接触载荷;δ 为接触变形量。

根据负荷和位移的方向不同，轴承刚度可分为径向刚度、轴向刚度和角刚度。双列角接触球轴承的动刚度是指轴承运动过程中的瞬时刚度，体现为钢球-滚道接触副的刚度。在考虑赫兹接触和弹性流体动压润滑的情况下，通过建立双列角接触球轴承钢球-滚道接触副的赫兹接触刚度和油膜刚度模型，推导双列角接触球轴承动刚度模型。

本文所研究的轴承为背靠背布置的双列角接触球轴承，其结构示意图如图1所示。坐标系Oxyz 为轴承的惯性坐标系。轴承外圈固定，两内圈通过一锁扣连结在一起以转速n 绕x 轴旋转。

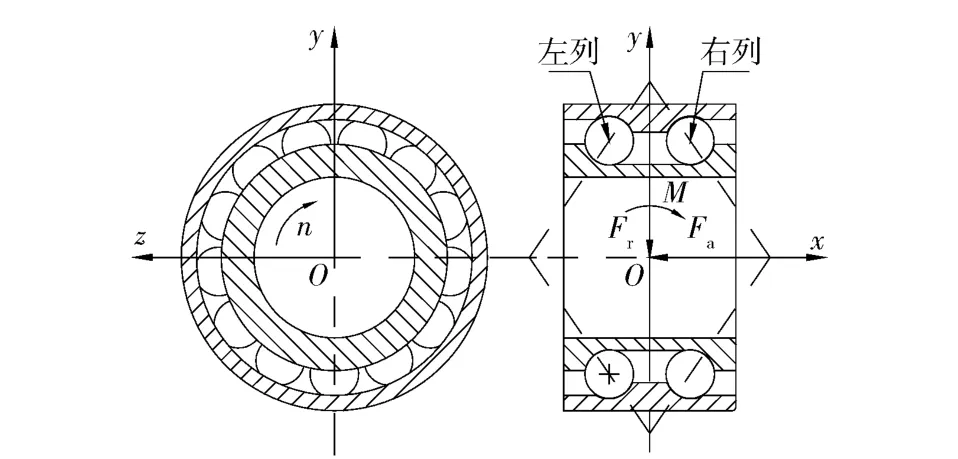
图1 双列角接触球轴承示意图Fig.1 Schematic diagram of double-row angular contact ball bearing

1.1 赫兹接触刚度

由经典赫兹接触理论可知，第j 个钢球与滚道接触时所产生的接触载荷为

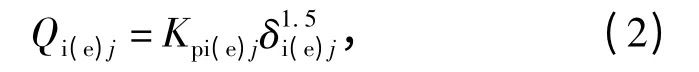
式中:Kpi(e)j为第j 个钢球与滚道接触处的负荷-变形常量，求解表达式见文献［4］;δi(e)j为第j 个钢球与滚道间的弹性变形量;下标i、e 分别表示内、外滚道(下同)。

由(1)式、(2)式可求得钢球与滚道间的赫兹接触刚度为

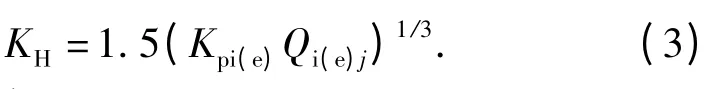
1.2 油膜刚度

根据弹性流体动力润滑理论，滚动轴承的油膜刚度由最小油膜厚度决定。Hamrak 等给出了等温条件下钢球与滚道间的最小油膜厚度计算公式［13］:

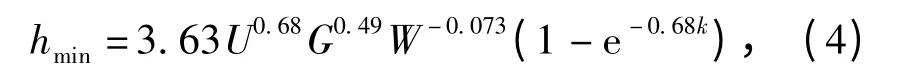
式中:U 为速度参数，U =η0vm/E*Rx，E*为当量弹性模量，η0为常压下润滑油的动力粘度，vm为表面平均速度;G 为弹性参数，G =αE*，α 为粘度的压力指数;W 为载荷参数，W =Q/E*Rx，Q 为接触载荷;k=1.03(Ry/Rx)，其中Rx、Ry分别为径向和轴向平面内的当量曲率半径。

将以上各参数带入(4)式并对其求导可得接触区油膜刚度为

1.3 轴承动刚度

通过建立钢球-滚道单接触副刚度模型，推导钢球与内外圈滚道的双接触副刚度模型，然后分别求得单列轴承的刚度，最后将两列轴承刚度并联起来求得整套轴承的刚度。

为便于研究，将钢球与滚道间的刚度简化为弹簧，钢球-滚道单接触副刚度计算分析模型，如图2所示。在第j 个钢球处，钢球-滚道单接触副的刚度Ki(e)j可由赫兹接触刚度KHi(e)j与油膜刚度KEi(e)j串联得到:

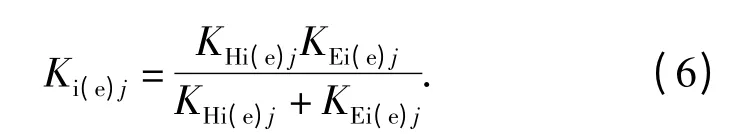
由图2可知，第j 个钢球与内外滚道间刚度的径向和轴向分量［10］为

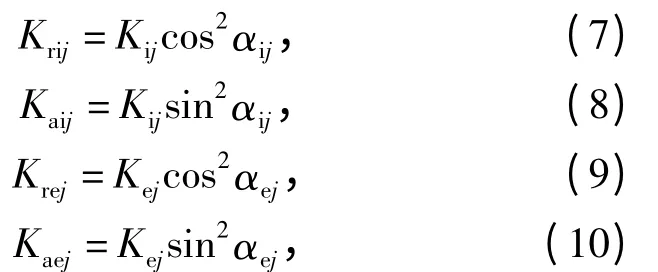
式中:αi(e)j为第j 个钢球与内、外滚道的接触角。

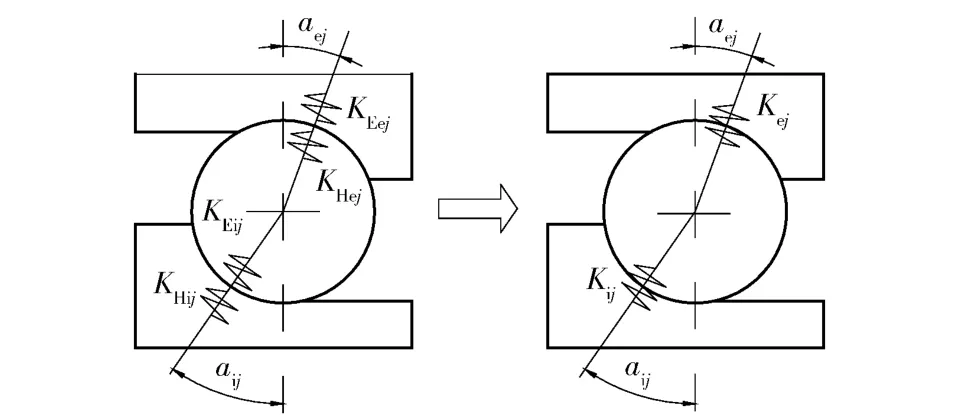
图2 钢球-滚道单接触副刚度模型Fig.2 Stiffness model of single-contact pair for ball-raceway

图3为钢球-滚道双接触副刚度计算分析模型。钢球-滚道双接触副刚度由钢球-外滚道接触副刚度与钢球-内滚道接触副刚度串联求得［14］。故第j 个钢球处双接触副刚度的径向和轴向分量为

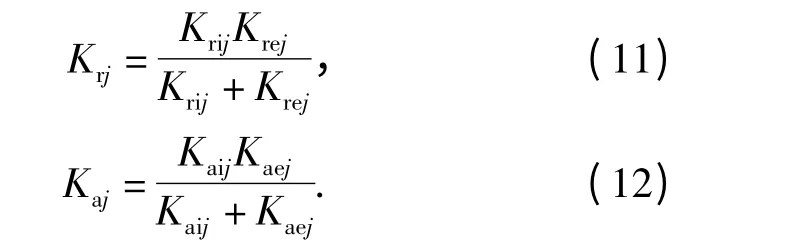
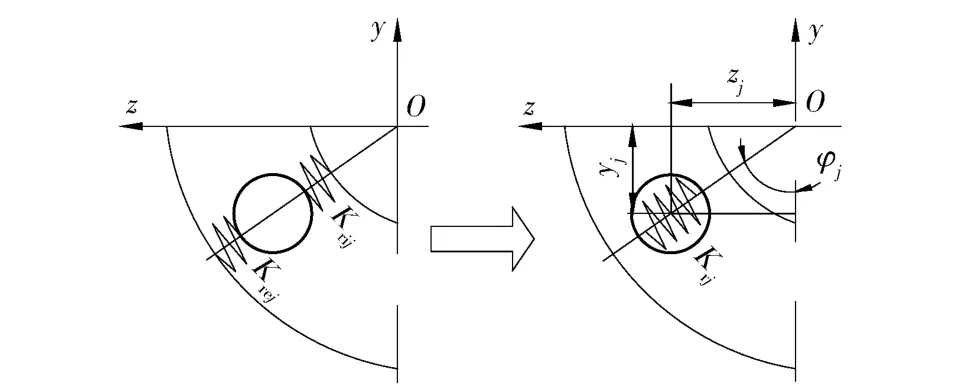
图3 钢球-滚道双接触副刚度模型Fig.3 Stiffness model of double-contact pair for ball-raceway

将每个钢球处钢球-滚道双接触副刚度的径向分量沿径向方向分解并按并联叠加，得到单列轴承的径向刚度KrL(R)为

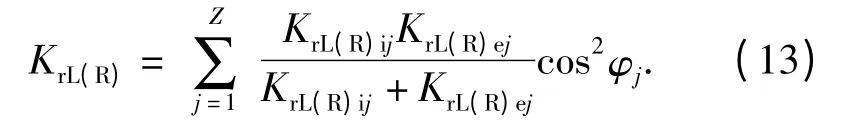
将每个钢球处钢球-滚道双接触副刚度的轴向分量并联叠加得到单列轴承的轴向刚度KaL(R)为

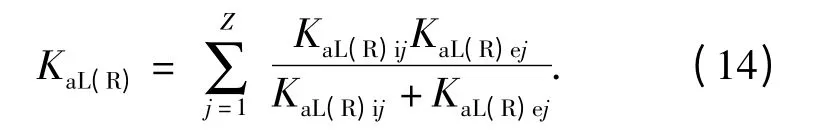
角刚度为抵抗角位移的能力，由钢球-滚道双接触副刚度的轴向分量与节圆直径决定［10］，

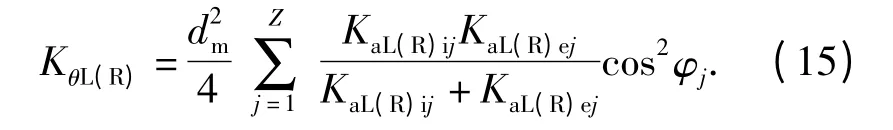
(13)式～(15)式中:下标L 和R 分别表示双列角接触球轴承的左列和右列(见图1);dm为轴承节圆直径;Z 为单列钢球数目;φj为第j 个钢球的方位角，由图3可得

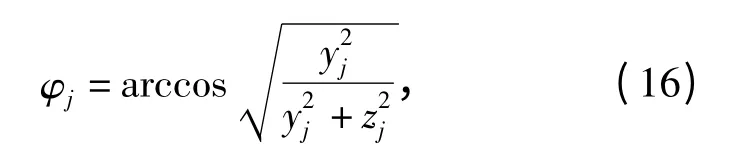
式中:yj和zj分别为第j 个钢球中心距轴承中心在y 方向和z 方向的距离。

分别求得单列轴承的径向刚度KrL(R)、轴向刚度KaL(R)和角刚度KθL(R)，将两列轴承刚度并联起来得到整套轴承的动刚度Kr、Ka和Kθ:

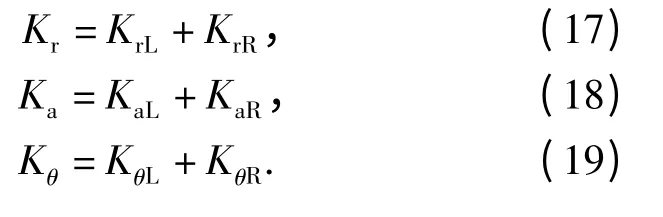
2 计算结果与分析

在双列角接触球轴承动力学分析基础上，建立双列角接触球轴承动刚度仿真分析模型，并采用精细积分法和预估-校正Adams-Bashforth-Moulton 多步法相结合的算法对该动刚度模型进行求解。本文以图1所示的某型号双列角接触球轴承为例，对轴承进行轴向定位预紧，分析了轴承结构参数与工况参数对其动刚度的影响。轴承主参数见表1，润滑油主要参数［11］见表2. 本文研究刚度时不考虑温度的影响，即润滑油的流变特性不变。

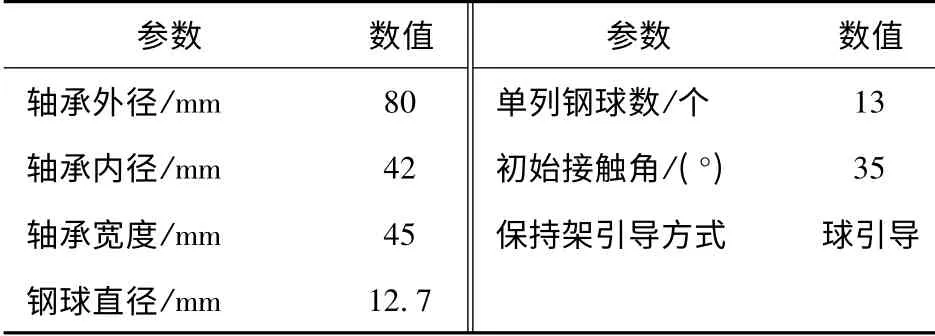
表1 轴承主参数Tab.1 Main parameters of bearing

表2 润滑油主要参数Tab.2 Main parameters of lubricating oil

2.1 结构参数对轴承动刚度的影响

轴承结构参数在很大程度上决定着轴承的动刚度。本文主要研究在轴承转速1 000 r/min 、径向载荷6 000 N、轴向载荷4 000 N、力矩载荷为0、单侧轴向预紧量为20 μm 的工况下，内、外沟曲率半径系数和钢球个数对其动刚度的影响。

2.1.1 沟曲率半径系数

沟曲率半径系数是球轴承设计的一个重要结构参数，它直接反映钢球与滚道的密合程度。图4为轴承动刚度随沟曲率半径系数变化的曲线。由图4可知，随着内、外沟曲率半径系数的增大，轴承径向刚度略有增加，轴向刚度和角刚度相对减小。这是由于沟曲率半径的增大使钢球与滚道间的密合度减小，赫兹接触变形量增大，接触角减小，故轴承动刚度呈现上述趋势。综合考虑沟曲率半径对轴承承载能力以及摩擦等其他特性的影响，该轴承内沟曲率半径系数取0.515，外沟曲率半径系数取0.525 较为合适。

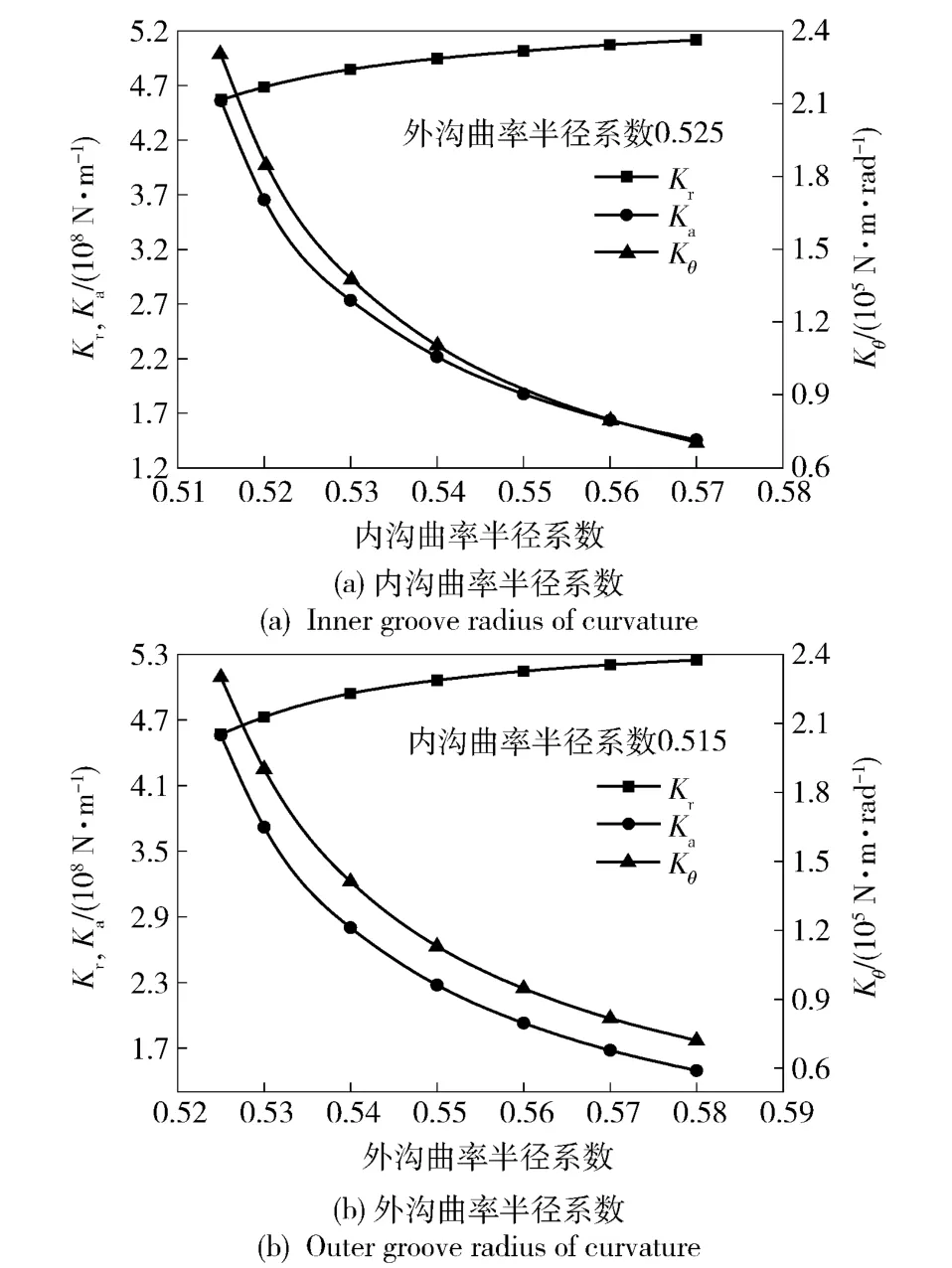
图4 动刚度随沟曲率半径系数的变化Fig.4 Dynamic stiffness vs. groove radius of curvature

2.1.2 单列钢球数

图5为轴承动刚度随单列钢球数变化的曲线。由图5可知，随着钢球数的增加，轴承径向刚度、轴向刚度和角刚度均增大。这是因为钢球数的增加使轴承受载钢球增多，钢球受载减小，与滚道间的赫兹接触变形量减小，故轴承刚度增大。因此，在满足保持架强度的前提下，应尽可能增加钢球个数。

2.2 工况参数对轴承动刚度的影响

2.2.1 轴承转速

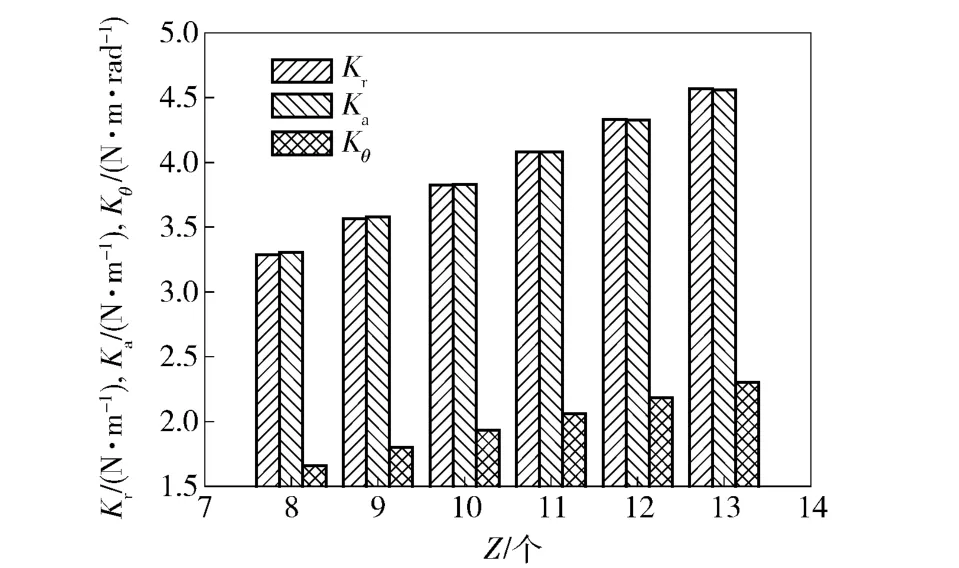
图5 动刚度随钢球个数的变化Fig.5 Dynamic stiffness vs. the number of balls

图6为径向载荷6 000 N、轴向载荷4 000 N、力矩载荷为0、单侧轴向预紧量为20 μm 时轴承动刚度随转速变化的曲线。由图6可知，油膜刚度随转速的增大而减小，且其减小速度逐渐降低;转速低于2 000 r/min 时，轴承动刚度和赫兹接触刚度均随转速的增大而略有减小，且二者较为接近，可近似用赫兹接触刚度代替轴承动刚度;当转速超过2 000 r/min后，动刚度和赫兹接触刚度随转速的增大而增大，此时，两曲线逐渐分开，轴承动刚度需由每个钢球处的赫兹接触刚度和油膜刚度按本文所建立的刚度模型综合求得。随着转速的增大，钢球“外抛”作用使外接触角减小，内接触角增大。同时，定位预紧下，轴向位移受到限制，预载荷随转速升高而增大，且最小油膜厚度随转速的升高而增大，故油膜刚度减小。在这些因素的共同影响下，轴承动刚度呈现上述趋势。

2.2.2 单侧轴向预紧量

双列角接触球轴承的预紧是影响其动态性能的重要因素之一。为使轴承的使用性能得到充分保证，需对其施加一定的轴向预紧。图7为轴承转速1 000 r/min 、径向载荷6 000 N、轴向载荷4 000 N、力矩载荷为0 时轴承动刚度随其单侧预紧量变化的曲线。由图7可知，在单侧预紧量由0 增大到30 μm过程中，径向刚度变化较小，轴向刚度和角刚度相对增大;当单侧预紧量大于30 μm 后，径向刚度、轴向刚度和角刚度均随预紧量的增大而急剧增大。这是由于轴向预紧量的增大使钢球与滚道间的接触角和接触载荷均增大，受载钢球个数增多，受载更加均匀，故轴承刚度呈现上述变化趋势。然而，预紧量的增加势必会降低轴承的使用寿命，因此在实际使用过程中，在满足寿命的前提下，增大轴向预紧量有助于提高轴承的动刚度。

2.2.3 径向载荷

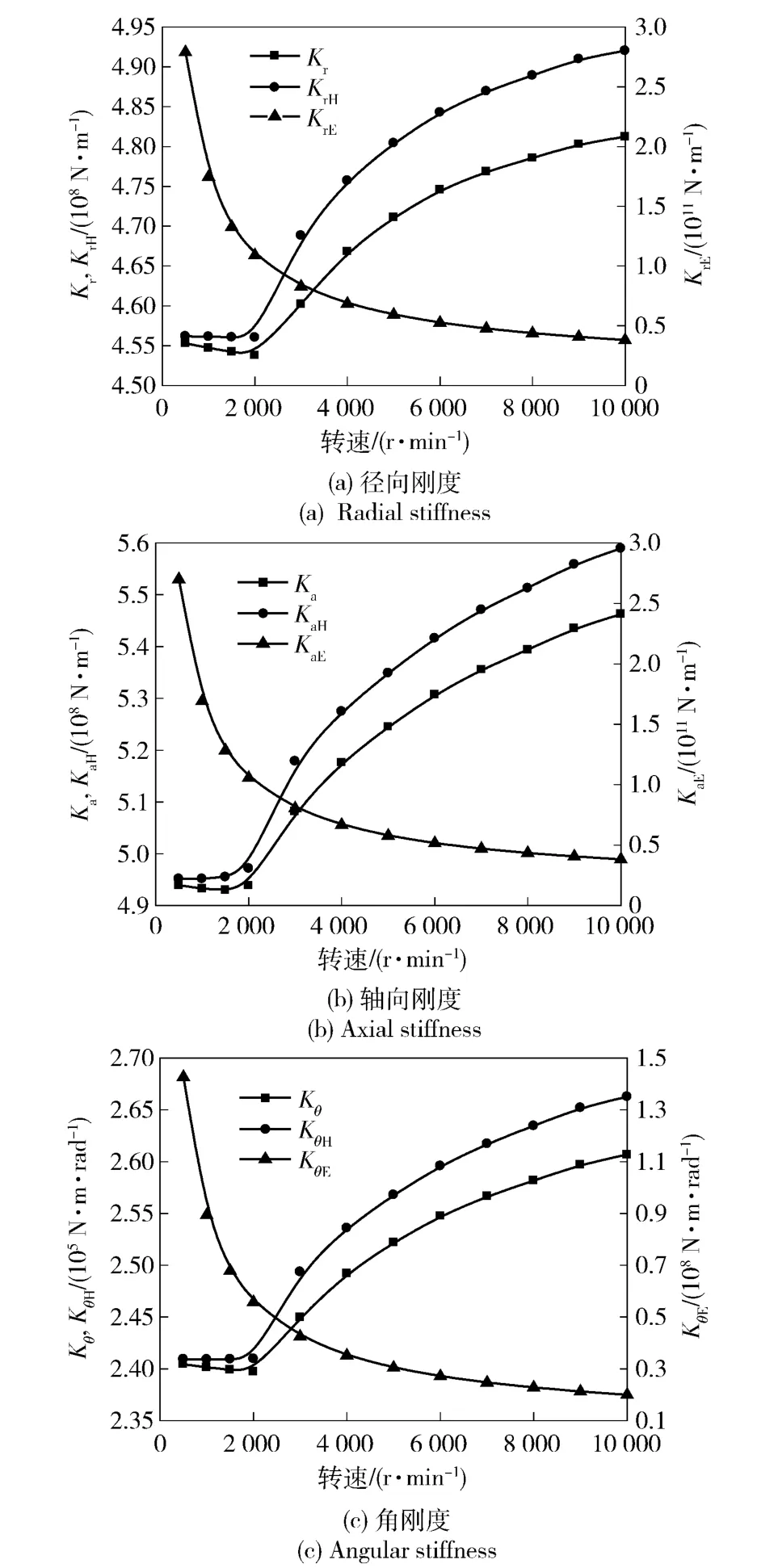
图6 动刚度随转速的变化Fig.6 Dynamic stiffness vs. rotating speed

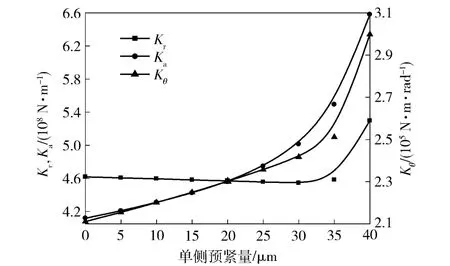
图7 动刚度随轴向预紧量的变化Fig.7 Variation in dynamic stiffness with axial preload

图8为轴承转速1 000 r/min 、轴向载荷4 000 N、力矩载荷为0、单侧轴向预紧量20 μm 时轴承动刚度随径向载荷变化的曲线。由图8可知，随着径向载荷的增大，轴承动刚度增大，其中径向刚度增大的速度最快。这是由于径向载荷的增大使钢球与滚道间的接触载荷增大，受载钢球增多，故轴承刚度增大。因此，对于双列角接触球轴承，根据应用场合对刚度的具体要求，径向载荷存在一个合适的范围。

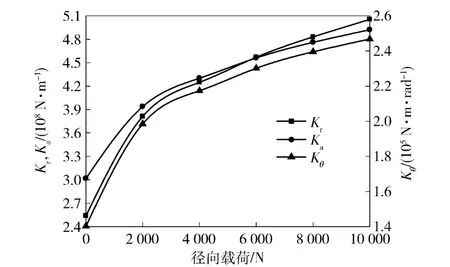
图8 动刚度随径向载荷的变化Fig.8 Dynamic stiffness vs. radial load

2.2.4 轴向载荷

图9为轴承转速1 000 r/min、径向载荷6 000 N、力矩载荷为0、单侧轴向预紧量20 μm 时轴承动刚度随轴向载荷变化的曲线。由图9可知，随着轴向载荷的增大，轴承动刚度增大，其中轴向刚度增大的速度最快。这是由于轴向载荷的增大使轴承左列被“放松”和右列被“压紧”的程度均增大，左列受载减小，接触角减小，右列受载增大，接触角增大，在接触载荷和接触角的共同影响下，左列刚度减小，右列刚度增大，轴承动刚度由左、右两列刚度叠加得到，呈增大趋势。故可根据刚度要求合理确定轴向载荷范围。

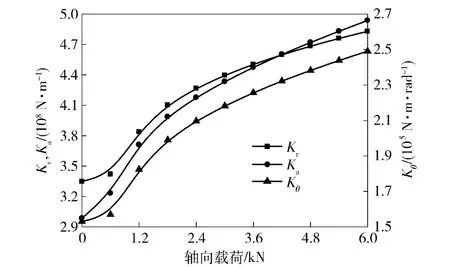
图9 动刚度随轴向载荷的变化Fig.9 Variation in dynamic stiffness with axial load

2.2.5 力矩载荷

图10 为轴承转速1 000 r/min、径向载荷6 000 N、轴向载荷4 000 N、单侧轴向预紧量为20 μm 时轴承动刚度随力矩载荷变化的曲线。由图10 可知，随着力矩载荷的增大，径向刚度呈先减小再增大然后又减小，最后增大的趋势，轴向刚度和角刚度呈现先减小再增大的趋势。轴承动刚度呈现上述变化趋势是由其受载特点决定的。在轴向载荷、径向载荷和力矩载荷的共同作用下(载荷加载见图1)，力矩载荷由0 增大到100 N·m 过程中，轴承左列下部承载区大小不变，但承载区内钢球的受力减小，导致左列刚度急剧减小，轴承右列由整圈受载减小为部分受载，且承载区内钢球受载波动性增大，钢球平均受载减小，故此过程中右列刚度也减小。力矩载荷由100 N·m 增大到400 N·m 过程中，左列承载区迅速扩大为全圈受载，且钢球受力增大，故左列刚度随力矩载荷的增大而增大;随着力矩载荷由400 N·m 增大到600 N·m，左列内圈角位移继续增大，下部部分钢球脱离内滚道，承载区减小，故此过程中左列刚度减小;力矩载荷继续增大，左列承载区不再减小，承载区内钢球受载随力矩载荷的增大而增大，故在此过程中，轴承左列刚度随力矩载荷的增大而增大。当力矩载荷大于100 N·m 之后，随力矩载荷的增大，轴承右列承载区不再减小，但承载区内钢球受载迅速增大，因此右列刚度随力矩载荷增大而增大。整套轴承的刚度是左右两列刚度并联求得的，其变化趋势由两列刚度的变化趋势叠加得到。

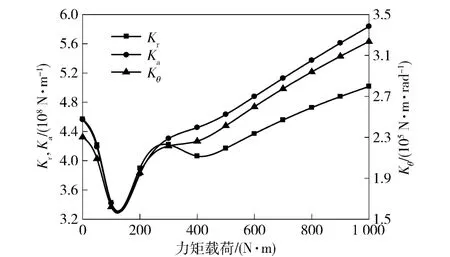
图10 动刚度随力矩载荷的变化Fig.10 Dynamic stiffness vs. moment load

3 结论

本文在双列角接触球轴承动力学分析基础上，建立双列角接触球轴承动刚度模型，采用精细积分法和预估-校正Adams-Bashforth-Moulton 多步法相结合的算法求解该刚度模型，研究了轴承结构参数和工况参数对双列角接触球轴承动刚度的影响，得出如下结论:

1)随着内、外沟曲率半径系数的增大，径向刚度略有增加，轴向刚度和角刚度相对减小;径向刚度、轴向刚度和角刚度均随钢球数的增加而增大。对于本文所研究的轴承，内沟曲率半径系数取0.515，外沟曲率半径系数取0.525，单列钢球数取13，有利于提高轴承动刚度。

2)增大轴向预紧有助于提高轴承动刚度，但过大预紧会使轴承寿命急剧降低。存在一个合理的预紧量使得轴承具有较好的刚度。

3)轴承转速较低时，动刚度随转速的增大略有减小，且可近似用赫兹接触刚度代替;当转速增大到一定值时，动刚度随转速的增大而增大，此时，需综合赫兹接触刚度和油膜刚度求解轴承动刚度。

4)外载荷对轴承动刚度有较大影响。加大径向载荷和轴向载荷有利于提高轴承动刚度，且轴向载荷对轴向刚度影响最大，径向载荷对径向刚度影响最大;力矩载荷对动刚度的影响较为复杂，但总体上，轴承动刚度随力矩载荷的增大呈现先减小后增大的趋势。对于双列角接触球轴承，针对不同应用场合对刚度的具体要求，可根据影响规律合理地确定轴承工作载荷的范围。

References)

［1］Wan C S. Analysis of rolling element bearings［M］. London:Mechanical Engineering Publications Limited，1991.

［2］Bourdon A，Rigal J F，Play D. Static rolling bearing models in a CAD environment for the study of complex system［J］. Journal Tribology，1999，121(2):215 -223.

［3］Szuminski P. Determination of the stiffness of rolling kinematic pairs of manipulators［J］. Mechanism and Machine Theory，2007，42(9):1082 -1102.

［4］Sarangi M ，Majumdar B C ，Sekhar A S . Stiffness and damping characteristics of lubricated ball bearings considering the surface roughness effect. Part 1:theoretical formulation［J］. Engineering Tribology，2004，218(5):529 -538.

［5］Sarangi M ，Majumdar B C ，Sekhar A S . Stiffness and damping characteristics of lubricated ball bearings considerating the surface roughness effect. Part 2:numerical results and application［J］.Engineering Tribology，2004，218(5):539 -547.

［6］Gunduz A，Singh R. Stiffness matrix formulation for double row angular contact ball bearings:analytical development and validation［J］. Journal of Sound and Vibration，2013，332(22):5898 -5916.

［7］Yi G，Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model［J］.Mechanism and Machine Theory，2012，51(5):32 -45.

［8］李松生，陈晓阳，张钢，等. 超高速时电主轴轴承动态支承刚度分析［J］. 机械工程学报，2006，42(11):60 -65.LI Song-sheng，CHEN Xiao-yang，ZHANG Gang，et al. Analysis of dynamic supporting stiffness about spindle bearings at extra high-speed in electric spindles［J］. Journal of Mechanical Engineering，2006，42(11):60 -65. (in Chinese)

［9］Hernot X，Sartor M，Guillot J. Calculation of the stiffness matrix of angular contact ball bearings by using the analytical approach［J］.Journal of Mechanical Design，2000，122(1):83 -90.

［10］杜迎辉，邱明，蒋兴奇，等. 高速精密角接触球轴承刚度计算［J］.轴承，2001 (11):5 -8.DU Ying-hui，QIU Ming，JIANG Xing-qi，et al. Calculation on rigidity of high speed precision angular contact ball bearing［J］.Bearing，2001 (11):5 -8. (in Chinese)

［11］王燕霜，邓四二，杨海生，等. 滚/滑接触中HKD 航空润滑油拖动特性试验研究［J］. 兵工学报，2009，30(7):958 -961 WANG Yan-shuang，DENG Si-er，YANG Hai-sheng，et al. Analysis of traction characteristics of HKD aviation lubricating oil in rolling/sliding contacts［J］. Acta Armamentarii，2009，30(7):958 -961. (in Chinese)

［12］Harris T A. Rolling bearing analysis［M］. 4th ed. New York:John Wiley ＆ Sons Inc ，1999.

［13］Hamrock B J，Dowson D. Ball bearing lubrication［M］. New York:John Wiley ＆ Sons Inc，1981.

［14］陈於学，王冠兵，杨曙年. 圆柱滚子轴承的动态刚度分析［J］. 轴承，2007(4):1 -5.CHEN Yu-xue，WANG Guan-bing，YANG Shu-nian. Analysis of dynamic stiffness of cylindrical roller bearings［J］. Bearing，2007 (4):1 -5. (in Chinese)