幂级数零点的詹逖生-斯泽古定理历史探析

王全来,曲安京

(1.天津师范大学 计算机与信息工程学院, 300387;2.西北大学 数学与科学史研究中心, 陕西 西安 710127)



·科学技术史·

幂级数零点的詹逖生-斯泽古定理历史探析

王全来1,曲安京2

(1.天津师范大学 计算机与信息工程学院, 300387;2.西北大学 数学与科学史研究中心, 陕西 西安 710127)

该文基于原始文献,利用历史分析和比较的方法，首次梳理了该定理发展的历史脉络(1900—1980),研究了该定理提出的历史背景,林德瓦特、波利亚和卢卡奇等人的工作为其思想基础;探讨了詹逖生和斯泽古在该定理上所做的工作,及该定理的进一步发展。深入分析了数学研究者的一些重要思想和方法,揭示了该定理所蕴含的思想内涵。

詹逖生;斯泽古;幂级数部分列;零点;聚点

幂级数部分列的零点分布研究是幂级数理论研究中的一个重要内容,该研究有许多重要的相关理论成果问世,詹逖生(R.Jentzsch,1890—1918)-斯泽古 (G.Szegö,1895—1985)定理即是其中之一。詹逖生-斯泽古定理首先由詹逖生在1914年的博士论文中提出,在1922年,斯泽古对詹逖生的结果做了深入探讨,成为其后许多数学家研究该问题的理论基石,故在许多数学著作中把该结果称为詹逖生-斯泽古定理。詹逖生-斯泽古定理经过数学研究者的不断努力,出现了诸多深刻结果。其结果散见于一些数学理论著作中,如文献[1-3]等。从历史角度对该定理进行论述和研究的,目前国内外尚未见到相关研究文献。鉴于此，基于原始文献,依据历史分析和比较的方法对该定理的历史发展进行研究,以补现有文献之不足。

1 詹逖生-斯泽古定理提出的思想背景

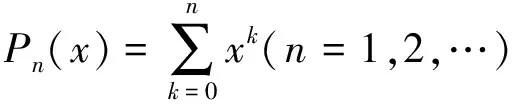
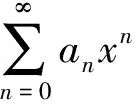
2 詹逖生和斯泽古在该定理上的工作

詹逖生在幂级数相关理论方面做出了奠基性的工作。他在1914年在弗罗贝尼乌斯(G.Frobenius,1849—1917)指导下完成博士论文《解析函数列理论研究》。弗罗贝尼乌斯和肖特基(F.Schottky)对其关于幂级数部分和及相关主题的论述感到钦佩。在对他的论文书面评价中,弗罗贝尼乌斯概述了詹逖生的结果,并写道:作者的结果远远超过了在这个领域所得的结果。他以相当简单的方式推导了他的主要结果。他的工作对于解析函数理论研究有很高的科学价值,堪称智力和聪明的典范[7]。他在文献[8]中证明了其称为的主定理,即詹逖生-斯泽古定理,该定理为部分列零点理论研究的理论基础。

詹逖生的主定理是幂级数部分列表现行为研究的结果,也是有关幂级数部分列大量重要研究的起点。当然,对于一般的多项式序列,詹逖生定理是不正确的。奥斯特洛斯基和斯泽古为了保证对于一般多项式序列的一致收敛区域的边界点是其零点的聚点分别在1922年给出了充分条件。稍后,斯泽古在文献[13]中给出了充要条件。

奥斯特洛斯基在文献[14]中考虑了解析函数列fn(z)在区域D的每个紧致集上一致收敛于f(z)的情况。他选择了D为最大可能区域,即所谓的一致收敛的完全区域。在对fn(z)的增长、收敛速度、f(z)的性质做各种假设下,他讨论了fn(z)的零点在E的一个特殊边界点的邻域内的各种情况,把詹逖生定理一般化。“三圆定理”是其结论证明的重要理论基础。

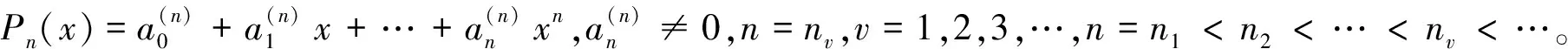
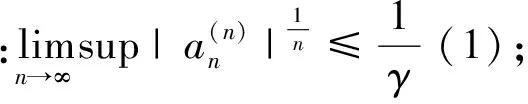
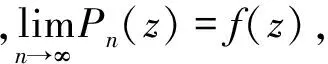
2)若在(1)中等号成立,则全部的Pn(z)的零点集合以|z|=1为聚点;

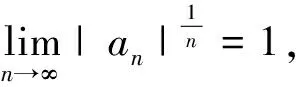
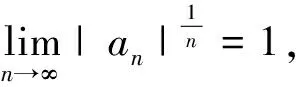
定理1)的证明采用了柯西不等式。2)和5)的证明为上述文章方法。3)和4)的推导方法依赖于方程根与系数的关系和反证法。斯泽古在该文末尾处指出,在收敛域不是圆的情况下上述结论依然成立。由上述结论可以看出,在1)中等号成立时,收敛区域的边界点为部分列零点的聚点的充要条件是k(n)=o(n)。

3 詹逖生-斯泽古定理的进一步发展

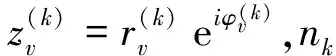
布洛赫(P.Bloch)和波利亚在1931年第一个给出了f(x)=a0+a1x+…+anxn的实数根R的上界估计问题。在1932年7月,在柏林大学数学学术讨论会上,施密特(Erhardt-Schmidt)告知舒尔(I.Schur),他得到了一个布洛赫和波利亚结果的一个加强定理。舒尔在文献[20]中指出,施密特基于函数理论方法,多次运用泊松-詹森(Poisson-Jensen)公式证得该定理。舒尔运用代数方法给出了一个新证明,并给出更为准确的结果。斯泽古在1934年进一步对舒尔的结果精确化,并且指出舒尔的最佳多项式为雅可比多项式。利特尔伍德(J.E.Littlewood)和奥福德(A.C.Offord)在1939年对施密特的结果给出了较为简单的证明[21]。埃尔德什(P.Erdös)和图兰(P.Turn)在文献[22]中给出了代数方程根的均匀分布定理,并指出詹逖生-斯泽古定理和施密特定理为该定理的推论。

施密特定理和詹逖生-斯泽古定理有一个共同来源的思想可能并不是新的。这可从舒尔在1934年3月3日递交给普鲁士科学院的物理数学专辑的报告中知晓。报告的内容只能从下面的内容中得知:“我将指出詹逖生具有有限收敛半径的幂级数部分列零点的定理可来自一个一般性的定理,不用函数理论工具证明。为了证明,可以利用矩阵方法对代数方程的根进行估计。”[22]埃尔德什和图兰在该文中指出, 在重要刊物和数学评论中未能找到舒尔关于包含了施密特定理的一个更为一般性的定理的任何内容。故他们对舒尔的说法表示怀疑。但无论如何,因为埃尔德什和图兰不使用矩阵方法,故应该与舒尔方法不同。

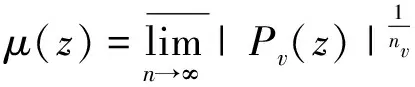
伊得来(A.Edrei)在研究Pade多项式的有关问题时把詹逖生-斯泽古定理推广到Pade逼近解析函数的分子上。在文献[25]中,他处理了解析函数有有限收敛半径的情况。在文献[26]中,他处理了阶是λ的整函数,0<λ≤∞。在文献[27]中在研究阿宾(A.Abian)猜想时,他把詹逖生-斯泽古定理推广到洛朗级数上,利用函数模理论和詹森公式进行证明。

沃尔什(J.L.Walsh)在研究最大收敛多项式在一个紧致集上逼近解析函数的问题时,采用蒙泰尔证明解析函数列零点定理的相关思路在文献[28]中证明了与詹逖生定理相类似的定理,指出若Eρ表示关于f解析的最大椭圆,则Pn(f)的零点在Eρ的边界上稠密。其中Pn(f)表示f的一致最佳逼近序列。特别是对f(z)恒等于0的特殊情况推广了詹逖生定理,其中特殊的雅可比级数为其推广的重要例证。博尔维恩(P.Borwein)在沃尔什工作的影响下,在文献[29]中探讨了在[-1,1]上连续函数的解析性质和最佳多项式逼近序列零点分布的关系,指出若逼近多项式序列在某个椭圆内无零点,则被逼近的函数在这个椭圆内一定解析。在该文中,他指出当E为单区间,且f为实值函数时,则若假设f在E内连续,而在E外不解析时隐含了至少存在E的一个点为最佳逼近多项式零点的聚点。他研究方法的理论依据为级数的系数模不等式、伯恩斯坦-詹科森定理。该问题由布拉特(H.P.Blatt)和萨夫(E.B.Saff)在文献[30]中得到了完美解答。他把沃尔什给出的詹逖生定理推广到ρ=1的情况,格林公式和沃尔什有关多项式逼近函数方面的研究定理为其重要的证明基础。

詹逖生-斯泽古定理是现代函数零点理论研究中的一个重要定理,该定理与其他数学分支的有机结合,呈现出不同的表述形式,揭示出深刻的数学思想内涵[32]。本文基于原始文献梳理了该定理发展的历史脉络,深入探讨了数学研究者们在该定理上所做的工作以及思想方法,为深入理解该定理在现代数学发展中的作用提供了重要史料。

[1] LANDAU E.Darstellung und Begrundung Einiger Neuerer Ergebnisse der Funktionentheorie[M].Berlin:Springer,1929.

[2] DIENES P.The Taylor Series:An Introduction to the Theory of Functions of a Complex Variable[M].London:Oxford University Press,1931.

[3] TITCHMARSH E C.The Theory of Functions[M].London: Oxford University Press.1939.

[4] HURWITZ A. Über die Nullstellen der Besselschen Funktion[J].Math Ann,1889, 33:246-266.

[7] DUREN P,HERBIG A K,KHAVINSON D.Robert jentzsch, mathematician and poet[J].The Mathematical Intelligencer,2008,30(3):18-24.

[8] JENTZSCH R.Untersuchungen zur Theorie der Folgen analytischer Functionen[J].Acta Math,1918,41:219-251.

[9] JENTZSCH R.Fortgesetzte Untersuchungen Über die Abschnitte von Potenzreihen[J].Acta Math,1918,41:253-270.

[10] OSTROWSKI A.On Representation of Analytical Functions by Power Series. Collected Mathematical Papers[M].Basel,Boston,Stuttgart:Birkhäuser Verlag,1984:159-171.

[11] ESTERMANN T.On Ostrowski’s gap theorem[J].Journ London Math Soc,1932,6:19-20.

[12] 王全来.奥斯特洛斯基在级数超收敛问题上的工作[J].内蒙古师范大学学报(自然科学汉文版),2013,42(6):708-712.

[13] SZEGÖ G. Über die Nullstellen von Polynomen,die in einem Kreis gleichmässig konvergieren[J].Sitzungsber Berl Math Ges, 1922, 21:59-64.

[14] OSTROWSKI A. Über Vollständige Gebiete Gleichmässiger Konvergenz von Folgen Analytischer Funktionen. Collected Mathematical Papers[M].Basel:Birkhäuser Verlag,1984:22-45.

[15] SZEGÖ G. Über die Nullstellen der Polynome einer Folge,die in einem einfach zusammenhängenden Gebiete gleichmässig konvergieren[J].Nach Ges Wiss Göttingen,1922,547-553.

[16] WOLFF J.Une généralisation d’un théorème de R.Jentzsch[J].C R Acad Sci Paris,1927,184:795-798.

[17] LUBELSKI S.Über das Verhalten der Abschnitte von Potenzreihen auf dem Konvergenzkreis[J].Math Ann,1934,109:230-234.

[18] DVORETZSKY A.On the theorem of Jentzsch[J].Proc Nat Acad Sci, 1949,35:246-252.

[19] DVORETZSKY A.On sections of power series[J].Annals of Mathematics,1950,51(3).643-696.

[20] SCHUR I.Untersuchungen Über algebraische Gleichungen.Ι:Bemerkungen zu einem Satz von E.Schmidt[J].Sitz Preu Akad Wiss, Phys Math Kl,1933,12:403-428.

[21] LITTLEWOOD J E,OFFORD A C.On the number of real roots of a random algebraic equation Ⅱ[J].Proc Camb Phil Soc, 1939,35:133.

[22] ERDOS P, TURAN P.On The Distribution Of Roots Of Polynomials[J].Annals of Mathematics,1950,51(1):105-119.

[23] GANELIUS T.Sequences of analytic functions and their zeros[J].Ark Mat,1954,3:1-50.

[24] ROSENBLOOM R C.Sequences of Polynomials, Especially Sections of Power Series[D].Dissertation: Stanford University,1943.

[25] EDREI A.Angular distribution of the zeros of Pade polynomials[J].J Approx Th,1978,24:251-265.

[26] EDREI A. The Padé tables of entire functions[J].J Approx Th,1980,28(1):54-82.

[27] EDREI A.Zeros of partial sums of laurent series[J].Mich Math J,1982,29:43-57.

[28] WALSH J L.The analogue for maximally convergent polynomials of Jentzsch’s theorem[J].Duke Math J,1959,26:605-616.

[29] BORWEIN P.The relationship between the zeros of best approximations and differentiability[J].Proc Amer Math Soc,1984,92:528-532.

[30] BLATT H P,SAFF E B.Behavior of zeros of polynomials of near best approximation[J].J Approx Theory,1986,46:323-344.

[31] BLATT H P,SAFF E B,SIMKANI M.Jentzsch-Szegö type theorems for the zeros of best approximants[J].J London Math Soc,1988,38(2):307-316.

[32] 徐传胜.伯恩斯坦的公理化理论及其概率思想研究[J].自然辨证法研究，2013(12)：15-20.

(编 辑亢小玉)

The research on the history of the theorem of Jentzsch-Szegö

WANG Quan-lai1， QU An-jing2

(1.The College of Computer and Information Engineering,Tianjin Normal University, Tianjing 300387， China; 2.Research Center for the History of Mathematics and Science, Northwest University, Xi′an 710127, China)

To discuss the distribution of the zeros of the sequences of the power series is important in the theory of the function. There are many results at present. Jentzsch-Szegö theory is one of the outcomes. This paper first analyses the historical context of the development of this theorem based on the original material by historical analysis and comparative methods. The historical background of the theorem was studied. The work of E.Lindwart, G.Polya and F.Lukãcs are the foundation.This paper discusses Jentzsch and Szegö’s work, and the development. It deeply analyses the important mathematical ideas and methods of the researchers, and reveals the idea connotations in the theorem.

R.Jentzsch; G.Szegö; the sequences of the power series; zeros; cluster point

2014-05-22

国家自然科学基金资助项目(11001199)

王全来,天津人,天津师范大学副教授,从事近现代数学史研究。

O173

：ADOI：10.16152/j.cnki.xdxbzr.2015-03-030