融合半监督降维与稀疏表示的人脸识别方法

融合半监督降维与稀疏表示的人脸识别方法

陈丽霞1，范士勇2，刘鑫1，王虹1，李昆仑1

(1.河北大学 电子信息工程学院， 保定 071002； 2.河北大学 计算中心， 保定 071002)

摘要：由于人脸图像数据的维数都较高，将稀疏表示分类用于人脸识别时计算量很大，为了提高人脸识别系统的效率，提出了一种融合半监督降维和稀疏表示的人脸识别方法。首先利用半监督降维算法对图像进行降维处理，在较低的维数空间快速取得较高的识别率，然后利用稀疏表示分类进行人脸识别，取得比传统的最近邻分类器更高的识别率，最后在ORL人脸库上进行实验验证。结果表明，利用该融合算法可快速有效地提高人脸图像的识别效果。

关键词：图像处理；人脸识别；半监督降维；稀疏表示

E-mail:clx@hbu.edu.cn

引言

人脸识别作为一种独特的生物特征识别技术，在计算机视觉和模式识别领域有着广泛的应用。但是人脸图像数据的维数很高，影响了人脸识别系统的识别效率，如何降低人脸图像的维数成为了一个研究热点[1]。最近，半监督降维技术引起了人们很大的关注，半监督降维有效综合了传统降维技术的优点，它既能利用数据的类标号信息又能保持数据的整体结构信息。

目前,稀疏表示分类(sparse representation-based classification,SRC)已经成功地应用到模式识别领域， WRIGHT提出将SRC用于人脸识别，该分类方法提高了人脸识别系统的识别率[2]。但是在人脸识别系统中，样本维数很高、SRC的计算量很大，因此需要寻找一种合适的降维方法，使得该算法能够在较低的维数空间里快速地提高人脸识别系统的识别率[3]。

综上所述，作者首先应用半监督降维算法对人脸图像进行降维提取人脸图像特征，再利用稀疏表示分类对人脸图像特征进行识别，这样既能保证人脸识别的精度又能保证人脸识别的速度[4]。

1理论分析

1.1　半监督降维算法原理

本节中主要研究半监督降维算法(semi-supervised dimensionality reduction,SSDR)。作者提供了一个基于成对约束信息的半监督算法的模型[5]。假设给定1组高维数据：X=[x1x2…xn]，其中xi∈Rf，半监督降维的目的就是找到n个对应的低维输出模型yi∈Re,e≪f,e和f代表数据的维数。假设X包含n个f维的数据并且包含一组成对约束，正约束M和负约束C。期望结果是从上述给定的条件下找到一个低维投影矩阵W=[x1x2…xd]，能够保证在低维空间同类的样本距离最小，不同类的样本应该尽量远离[6]。最后，将高维空间数据转换到低维空间数据时得到一个转换模型f(x),数据在低维空间可以表示为Y=f(x)=WTX。为此定义目标函数为J：

式中,α和β是权衡参量，Sij是判别相似度矩阵。

(1)式可以表示成:

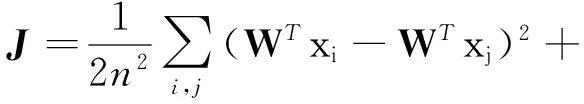
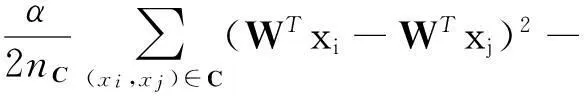
式中，D是一个对角矩阵，对角线上的值是相似度矩阵S的行或列的总和，L=D-S是Laplacian矩阵。矩阵XLXT是对称矩阵，可以通过求解广义特征值问题得到目标函数的向量wi。经过上述处理可以将测样本经过SSDR得到其在低维空间的投影Y，即Y=WTX。

1.2　稀疏表示分类算法原理

稀疏表示分类算法的主要思想是：假设测试样本都可以通过属于同一类别的部分训练样本来重构，仍然可以保持同样的重构精度，并且线性重构权值向量满足一定的稀疏性[7]。

具体模型如下:将每个人脸图用一个向量表示，设第i类的样本矩阵Ai=[ai1ai2…aini]∈Rm×ni，m表示人脸图像的特征维数，ni表示第i类样本的数量。根据假设属于第i的测试样本y就可以用A的线性组合表示，即：

式中，xij∈R,j=1,…,ni，在这里测试样本的类别是未知的，将k类训练样本组合在一起构成字典：A=[A1A2…Ak]=[a11a12…a1n1…ak1…aknk]，则属于第i类的测试样本y可以表示为:

式中，x0=[00…0xi1…xini0…0]T∈Rm是一个稀疏系数向量，理想情况下只有第i类样本空间的系数不为0，其它均为0。

对于人脸识别系统问题，通过上述方程,求得最稀疏解,得到对应的x0。由于人脸图像数据都是高维的，所以都需要降维，经过降维之后的样本构成的方程组是欠定的，即m

上述求解过程是一个非确定性问题，难以求解。基于压缩感知与稀疏表示方法理论研究表明：当样本数量达到足够稀疏时，L0范数最小化问题就等价于L1范数最小化问题[9]：

分类的结果可以表示为使上式最小化的参量i所对应的值argminri(y)。

2实验结果和分析

本文中的实验环境为惠普笔记本，CPU1.6GHz，内存3GB，MATLAB 7.1，采用的数据库为ORL人脸库。ORL人脸图像数据库包含40个人，每人10幅，共400张人脸图像，包括了姿态、表情和面部饰物的变化。该人脸库在是较早用于各项人脸识别中的标准人脸库。

在实验中选取ORL人脸库中22个人(每人10幅)的220幅图像作为样本，选取前5张的人脸图像作为测试样本，如图1所示。本文中分别采用最近邻(nearest neighbor,NN)分类器[11]和SRC分类器，将人脸图像数据利用不同方法降维到不同的特征维数下进行分类。实验结果见表1和表2。

Fig.1　Example images in ORL database

Table 1NN classification after PCA and SSDR dimensionality reduction on ORL database

methoddimension30507090110PCA63%64.4%64.9%65%67%SSDR89%90%90.97%92%94%

Table 2SRC classification after PCA and SSDR dimensionality reduction on ORL database

methoddimension30507090110PCA86%87%90%93%94%SSDR91%93%93.75%95%96%

从表1可以看出,利用SSDR方法降维后人脸系统的识别率明显优于利用主成分分析(principal component analysis,PCA)[12]降维后人脸系统的识别率，这是因为SSDR方法既能利用人脸图像样本的大量无标记样本，又能利用样本间的成对约束信息，这样就可以更好地保持人脸数据的全局和局部结构。而PCA算法只利用了人脸图像样本的无标记样本，容易产生错分类的现象。

利用SRC分类器后的分类结果如表2所示。可以看到，SRC分类器能够取得比传统的NN分类器更好的性能，融合半监督降维和SRC分类器进行人脸识别的识别率远远高于其它算法的识别率，并且随着特征维数的增高识别率有着显著提高。

3结论

提出了一种融合半监督降维与稀疏表示的人脸识别方法，既可以提高人脸识别的精度又能够提高人脸识别的速度。在ORL人脸库进行的实验表明，本文中提出的融合算法比传统的数据算法取得了更高的识别率,识别精度达到了96%。

参考文献

[1]HUA G,YANG M S. Introduction to the special section on real word face recognition[J].Pattern Analysis and Machine Intelligence,2011,33(10): 1921-1924.

[2]WRIGHT J,YANG A,GANESH A. Robust face recognition via sparse representation [J]. Pattern Analysis and Machine Intelligence, 2009,31(2): 210-227.

[3]HUANG W L,YIN H J.On nonlinear dimensionality reduction for face recognition [J]. Image and Vision Computing,2012,30(4):355-366.

[4]GAO Y,WANG F H,GUO Sh X.Application of improved wavelet transform algorithm in image fusion[J].Laser Technology,2013,37(5): 690-695(in Chinese).

[5]CHEN Sh G, ZHANG D Q.Experimental comparisons of semi-supervised dimensional reduction methods[J]. Journal of Software,2011,22(1):28-43.

[6]YAN S,BOUAZIZ S, LEE D W.Semi-supervised dimensionality reduction for analyzing high-dimensional data with constraints[J]. Neurocomputing,2012,76(1):114-124.

[7]HUAN K K.Regularized marginal fisher analysis and sparse representation for face recognition[J]. Journal of Computer Applications, 2013,33(6):1723-1726(in Chinese).

[8]GU X H.Visual perception and edge preserving illumination invariant face recognition[J].Acta Electronica Sinica,2013,41(8)：1500-1504(in Chinese).

[9]ZUO Y Y,GAO B.Robust hierarchical framework for image classification via sparse representation[J].Tsinghua Science and Technology,2011,1(1):13-21.

[10]YANG M, ZHANG L, YANG J,etal.Metaface learning for sparse representation based face recognition[C]//2010 17th IEEE International Conference on Image Processing.New York,USA:IEEE,2010: 1601-1604.

[11]HU H F.Orthogonal neighbourhood preserving discriminant analysis for face recognition[J].Pattern Recognition,2008,41(6):2045-2054.

[12]TURK M, PENTLAND A. Eigen-faces for recognition [J]. Jounal of Cognitive Neuroscience,1991,3(1):71-86.

Face recognition based on semi-supervised dimensionality

reduction and sparse representation

CHENLixia1,FANShiyong2,LIUXin1，WANGHong1,LIKunlun1

(1.College of Electronic and Information Engineering, Hebei University, Baoding 071002, China;2.Computer Center, Hebei University, Baoding 071002, China)

Abstract：Because of high dimensions of face image data and large calculation of sparse representation classification for face recognition, in order to improve the efficiency of face recognition system, a new face recognition method based on semi-supervised dimensionality reduction(SSDR) and sparse representation (SR) was proposed. Firstly, SSDR algorithm was used to reduce the image dimensions and achieve higher recognition rate in the lower dimension space quickly. Secondly, SR classification can achieve a higher recognition rate than the nearest neighbor classification in face recognition. And then, the experimental verification was demonstrated on ORL face database. The results show that the fusion algorithm can improve the recognition performance of face images quickly and effectively.

Key words:image processing; face recognition; semi-supervised dimensionality reduction; sparse representation

收稿日期：2014-01-02；收到修改稿日期：2014-02-28

作者简介:陈丽霞(1982-),女,实验师,主要研究方向为图像处理和模式识别。

基金项目：国家自然科学基金资助项目(61204079)；河北省自然科学基金资助项目(F2013201170;F2013201196)； 河北省科技厅软科学资助项目(12450328)；河北大学2012年度实验室开放基金资助项目(2012027)

中图分类号：TP391

文献标志码：A

doi:10.7510/jgjs.issn.1001-3806.2015.01.016

文章编号：1001-3806(2015)01-0082-03