开封典型土含水率对抗剪强度的影响研究
杨二静,胡 涛
(黄河水利职业技术学院,河南 开封 475004)
开封典型土含水率对抗剪强度的影响研究
杨二静,胡 涛
(黄河水利职业技术学院,河南 开封 475004)
含水率变化对土的抗剪强度影响较大,非饱和土的抗剪强度,影响工程实施。分析非饱和土抗剪强度理论研究现状;取开封土样,采用直接快剪试验方法得到不同含水率土样的抗剪强度;分析试验数据,得到含水率变化对抗剪强度的影响规律。
开封土样;含水率;抗剪强度;黏聚力;内摩擦角
0 引言
在工程建设实践中,道路的边坡、路基、土石坝、建筑物的地基等土体的破坏大多是因为土体的抗剪强度不足所致。土的抗剪强度是指土体抵抗剪切破坏的极限强度,现实中表现为:在表面不水平的情况下,土体仍然能够保持平衡。如果土的含水率很大,处于流动状态,则其不存在抗剪强度;非流动状态下,土具有抗剪强度,但其含水率的大小对土的抗剪强度影响很大[1]。例如,在海滩上,用潮湿的沙土可以塑成城堡等各种造型,而干燥和饱和状态的沙土则不能。
土的抗剪强度主要受土体的矿物成分、内部结构以及含水率的影响。实际工程中,对于特定地区特定范围内的工程土体来说,土体的矿物成分、内部结构与密度在局部范围内的变化一般不大。但是,由于受蒸发、降雨、灌溉等因素的影响,土体的含水率变化往往很大。为了保证工程建设的正常施工和安全运营,需要研究含水率对土的抗剪强度的影响。
1 土的抗剪强度理论研究现状
1.1 莫尔-库伦理论
法国学者库仑(C·A·Coulomb)对沙土进行了大量的试验研究,得出沙土的抗剪强度的表达式为公式(1)。后来,又进一步提出了黏性土的抗剪强度表达式,即公式(2)。

式中:τf为土的抗剪强度,kPa;σ为剪切面上的正应力,kPa;φ为土的内摩擦角。

式中:c为土的内黏聚力,kPa。
式(1)和式(2)分别表示沙土和黏性土的抗剪强度规律,通常统称为库仑定律。根据库仑定律可以绘出库仑直线图。其中,库仑直线与横轴的夹角称为土的内摩擦角φ,库仑直线在纵轴上的截距c为内黏聚力。
由库仑定律可以看出,在剪切面上的法向应力σ不变时,试验测出的φ、c值能反映出土的抗剪强度τf的大小,故称φ、c为土的抗剪强度指标。但是,抗剪强度指标φ、c不仅与土的性质有关,而且与测定方法有关。在不同试验条件下,同一种土体测出的强度指标不同。因此,谈及强度指标φ、c时,应注明它的试验条件。
1.2 饱和土有效应力原理修正莫尔-库伦理论
1925年,太沙基提出了饱和土的有效应力原理。他认为,对抗剪强度起决定作用的是有效应力,而不是总应力,并对库仑定律进行修正。修正后的库仑定律表达式为公式(3)。

式中:c′为有效黏聚力;uw为孔隙水应力;(σuw)为破坏面上的有效正应力;φ′为有效内摩擦角。
修正后的库伦公式预测饱和土的抗剪强度被岩土界普遍认可。此时,人们也才认识到饱和土的抗剪强度可以用太沙基修正的库仑定律计算。但是,非饱和土抗剪强度的研究还是空白。直至目前,规范中还是用公式(1)、(2)和(3)来确定土的抗剪强度。
1.3 非饱和土抗剪强度研究
1960年,Bishop提出基于饱和土强度理论的非饱和土有效应力的抗剪强度理论,其表达式为公式(4)。
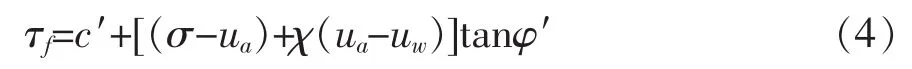
式中:ua为孔隙气压力;χ为与土的饱和度有关的参数,取值范围为0~1.0;(ua-uw)为基质吸力。
Bishop是通过扩展太沙基的饱和土有效应力原理,得到非饱和土的有效应力原理,并结合莫尔-库伦理论,得到非饱和土的抗剪强度公式。可见,Bishop是从原理上进行的公式推导,并未给出χ值的确定方法。由于影响χ值的因素众多,无法确定准确,所以公式(4)没有在工程实践中得到广泛的应用。
1978年,Fredlund提出以正应力与吸力作为变量的非饱和土抗剪强度公式,其表达式为公式(5)。
τf=c′+(σ-uw)tanφ′+(ua-uw)tanφb(5)
式中:φb为抗剪强度随基质吸力而增加的速率。
1996年,Vanapalli将φb与土的体积含水率的变化通过土—水特征曲线(SWCC曲线)联系起来,得到公式(5)中φb与土的体积含水率间的关系,进而得到公式(6)所示的非饱和土抗剪强度公式。

式中:θs为饱和土中的体积含水率;θr为残余体积含水率。
用SWCC曲线方程得到公式(4)中有效应力参数χ的值为

Yang通过击实土的相关实验得出,吸附强度和含水率之间的关系是线性的,并提出非饱和土的抗剪强度公式,即

式中:w为含水率;θw为体积含水率;ws为饱和含水率。
1986年,Lamborn的实验研究也提出了相关的非饱和土抗剪强度公式,其与式(8)相似,为公式(9)。
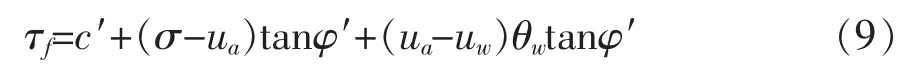
1998年,Khalili认为,虽然公式(4)中有效应力参数χ很难测量,但是可以通过收集数据得出一个经验性的χ的表达式。Khalili通过分析14种不同种类的土的剪切强度试验,得到有效应力参数χ和基质吸力(ua-uw)的log值存在近乎于直线的关系,斜率从0.4~0.65之间变化(代表黏土到沙土的变化)。其表达式为公式(10)和公式(11)。
当(ua-uw)>ue时:

当(ua-uw)≤ue时:

式中:ue为进气值。
此外,还有沈珠江折减吸力的双曲线抗剪强度公式、汤连生的湿吸力概念的抗剪强度公式、王钊和缪林昌的双曲线抗剪强度公式。
综上所述,自1960年Bishop提出基于饱和土强度理论的非饱和土强度理论以来,对于非饱和土抗剪强度的研究已有50多年的历史,从以上所提各种非饱和土的抗剪强度公式中可以看出,非饱和土的抗剪强度主要由黏聚力、破坏面上有效压应力产生的摩擦力和吸力引起的吸附强度3部分组成。学者大多都同意黏聚力和摩擦强度的表达形式,但却对吸附强度的确定方法看法不同。
公式(5)、(6)、(9)、(10)(11)中的吸附强度一项都需要借助SWCC曲线确定。SWCC曲线是用来描述非饱和土中的基质吸力(ua-uw)与体积含水率、重量含水率或饱和度等之间关系的重要曲线。但是,关于SWCC曲线的研究还不完善,其研究工作的关键环节是准确测量基质吸力。目前,国内外基质吸力的量测方法可分为直接测量法(压力板仪和张力计)和间接测量法(热传导吸力探头、热偶湿度计、石膏电阻计和滤纸法)。这些量测方法都没有考虑试验中土样的体积变形 (如沙土在剪切时会存在剪胀或减缩的现象)和竖向压力或平均应力对非饱和土的影响。
2 土样的物理性能参数试验
理论公式的获得一般有两种途径:(1)从试验中发现规律性的东西,然后将该规律用方程拟合。(2)已有理论基础加上个人推理,得到理论公式,然后用试验结果进行验证。可见,无论采用哪种途径,试验结果至关重要。为了得到含水率对抗剪强度的影响规律,又避开吸力量测的困难,本文利用开封常见的粉质沙土,制备重塑土样,采用应变式直剪仪,进行直接快剪试验。
以开封某工程土样为例,取风干土样2 520 g,用筛分法做颗粒分析试验,实验数据如表1所示。
根据表1的试验数据,可绘制该土样的颗粒级配曲线如图1所示。再从粒径小于0.075mm的土中取15 g,用密度计法测出细粒组中粉粒含量超过50%,得出细粒部分为粉土[2]。根据《土的工程分类标准》(GB/T 50145-2007),将该土样命名为粉土质沙[3]。kPa、200 kPa和400 kPa,测出各土样剪切破坏时的剪应力。
3.2 直接剪切试验数据
不同含水率土样的直剪试验结果如表2所示。

表1 筛分法试验数据Table 1 Test data of screening method
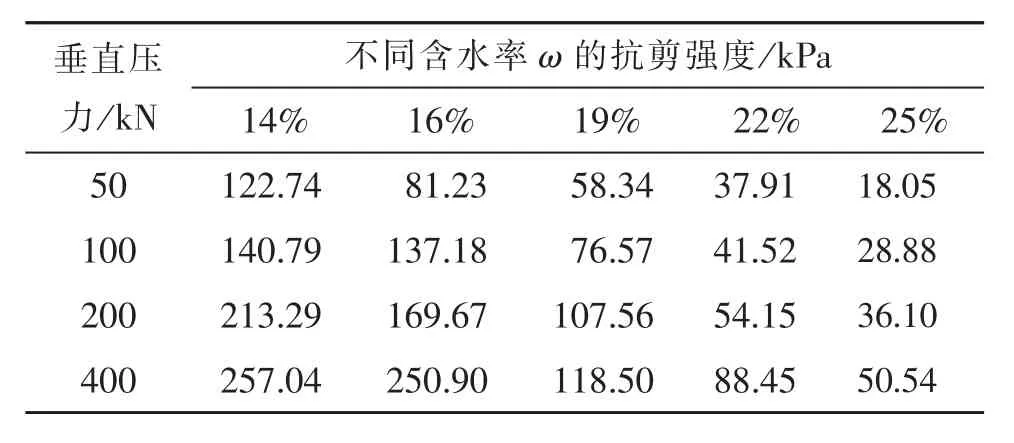
表2 土样不同含水率时的直剪试验数据Table 2 Direct shear test data of soil samples of different moisture content

图1 土样的颗粒级配曲线Fig.1 Grading curve of soil samp le
3.3 试验结果分析
(1)在半对数坐标系中,绘制相同垂直压力下,含水率ω与抗剪强度τ的对数的关系曲线,如图2所示。由图2可知,在相同垂直压力下,logτ与含水率呈线性关系,随含水率ω增加而减小。

图2 不同垂直压力时ω与 logτ关系图Fig.2 Relations ofωand logτof different vertical pressure
3 直接剪切试验数据及试验结果分析
3.1 试验方法
(1)制备含水率分别为14%、16%、19%、22%和25%的重塑土样。取风干土样(含水率为1%)5份,每份880 g,分别按最终含水率为14%、16%、19%、22%和25%计算加水量,加入蒸馏水,搅拌均匀,用保鲜膜覆盖保湿,静置24 h以上。用击样器以相同的高度和次数将不同含水率的土样分别击入重塑桶中,保证击实后土样的干密度相同。然后,用环刀切取每种含水率的击实土样各4个,切取的土样放入塑料袋保湿。
(2)采用应变式直剪仪进行快剪试验。对每种含水率下的4个土样,分别施加垂直压力50 kPa、100
(2)根据4组不同含水率下土样的直剪试验数据可以点绘出库仑直线(如图3所示),由此求出土的抗剪强度指标c、φ(如表3所示)。
(3)根据表3,可绘制出抗剪强度指标-含水率曲线 (如图4所示)和内摩擦角-含水率关系曲线(如图5所示)。
由图4可见,黏聚力随含水率的增加而减少。这是因为,黏性土的含水率从0增加时,先是以强结合水的形式存在,土粒间的结合水的联结力很大,土粒间不易相互错动,表现为土的黏聚力很大;含水率继续增加会使结合水膜加厚,以弱结合水的形式存在,土粒间结合水的联结力将减弱,表现为土的黏聚力变小;含水率继续增加,水在土中以自由水的形式存在,土粒间的联结力继续减小,土的黏聚力也继续减小[4]。
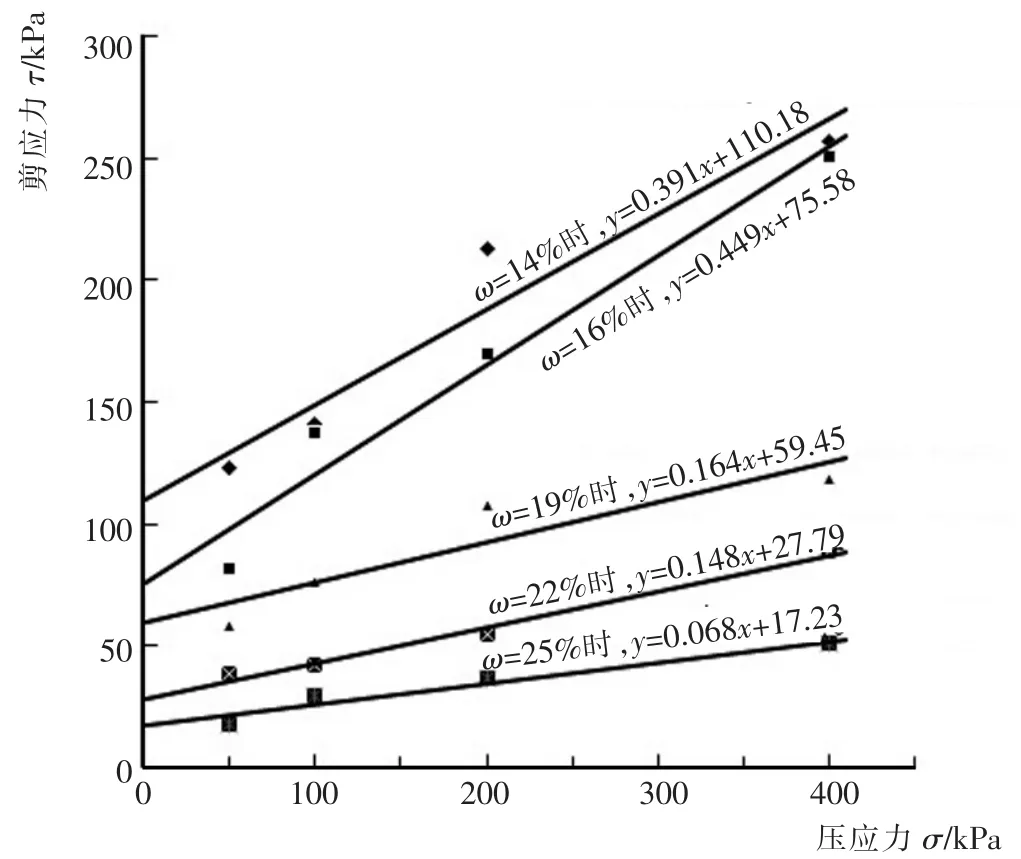
图3 不同含水率的τ与σ关系图Fig.3 Relations ofτandσw ith different moisture content

图4 c-ω关系图Fig.4 Relations of c-ω
用常规直接剪切试验方法所求得的黏聚力c值中包含有稳定的真黏聚力和不稳定的表观黏聚力两部分,其中表观黏聚力强度较大,受含水率影响也很大。该土样含水率在14%~19%时,黏聚力大的不正常,这可能是不稳定的表观黏聚力造成的。
由图5可知,含水率的变化对内摩擦角的影响十分明显。土中的含水率增大时,水在土体中起到一种润滑作用,会降低土粒表面上的摩擦力,使土的内摩擦角φ值减小。

图5 φ-ω关系图Fig.5 Relations ofφ-ω
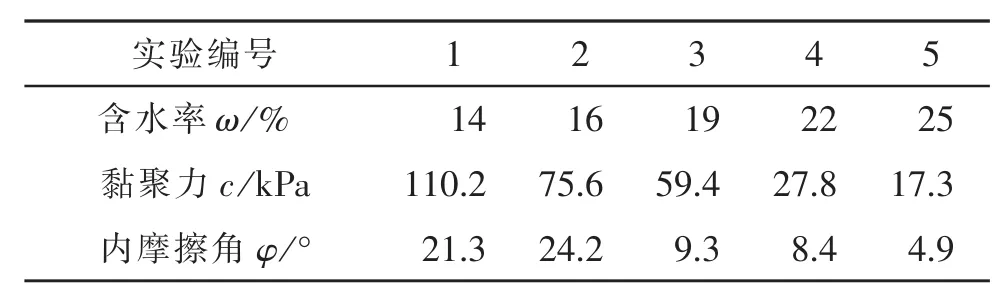
表3 不同含水率土的抗剪强度指标Table 3 Shear strength indexes of soil w ith different moisture content
4 结语
综上试验结果分析发现:(1)相同垂直压力下,与含水率呈线性关系,且logτ随含水率ω增加而减小。(2)同一含水率,垂直压力越大,抗剪强度越大。(3)垂直压力越大,含水率的变化对抗剪强度影响越大。
[1]王玉珏,孙其龙.工程地质与土力学[M].郑州:黄河水利出版社,2012:56-90.
[2]GB/T 50123-1999,土工试验方法标准[S].
[3]GB/T 50145-2007,土的工程分类标准[S].
[4]边加敏,王保田.含水量对非饱和土抗剪强度参数的影响研究[J].地下空间与工程学报,2011(1):17-21.
[责任编辑 杨明庆]
TU432
B
1008-486X(2015)02-0024-04
2015-01-13
黄河水利职业技术学院青年科研基金项目:含水率对开封典型土抗剪强度的影响研究(2013QNKY001)。
杨二静(1980-),女,河南西华人,讲师,硕士研究生,主要从事水利工程专业的教学与研究工作。

