有限温度第一原理热力学：关于处理有序相和无序相的观点

商顺利, 王　义, 刘梓葵

(宾夕法尼亚州立大学材料科学与工程系, 美国 宾夕法尼亚州大学城, PA 16802)



特约专栏

Received date：2014-12-22

Corresponding author：Shunli Shang,Senior Research Associate,Email:sus26@psu.edu

CLC number：TG111Document code： AArticle ID：1674-3962(2015)04-0297-08

有限温度第一原理热力学：关于处理有序相和无序相的观点

商顺利, 王义, 刘梓葵

(宾夕法尼亚州立大学材料科学与工程系, 美国 宾夕法尼亚州大学城, PA 16802)

摘要：第一原理计算一个悬而未决的难题是预测无序相在有限温度下的热力学性能。作者团队指出该难题的最新解决思路是采用可以处理微观组态的配分函数方法，该方法已成为处理只有一种主要微观组态构成的有序相以及有多种明显的微观组态构成的无序相的关键。结合第一原理声子计算和准简谐近似可以有效地预测任意一个给定微观组态的热力学性质。总结了作者团队在第一原理热力学方面的最新研究进展并具体给出了有序相方面的例子：Li2S, hcp Mg和fcc Ni,以及无序相方面的例子：Cu2ZnSnS4(CZTS) 和fcc Ce。同时指出：①从常用的“相”扩展到“微观组态”开辟了一条定量研究材料相变、热膨胀等异常性能的新途径，而这些异常性能的起源可以追溯到“微观组态构型熵”；②这些微观组态也可以认为是材料基因组的基本组成模块。

关键词：第一原理声子计算;准简谐近似;微观组态;有序相;无序相;热力学性质

1Introduction

Great success has been made in recent years in first-principles thermodynamics of ordered phases with the input being atomic numbers and crystal structures[1]. Furthermore with the quasiharmonic approach[2-3], the density functional theory (DFT) based first-principles calculations yield quantitative Helmholtz energy as a function of volume and temperature for a given structure, i.e., the ordered phase. However, the treatment of disordered phase due to uncertainty of atomic occupations still remains one of the longstanding issues within the first-principles community[4]. After years of efforts, two approaches are widely used for substitutionally disordered phases[4]: the cluster expansion method (CEM)[5-7]and the special quasirandom structure (SQS)[8-9]. In CEM, first-principles energetics of a variety of structures (microstates) with each possessing a specified configuration is mapped onto a generalized Ising-like Hamiltonian to determine the effective cluster interactions (ECI’s), and then, the lowest energy configurations as well as energies for disordered configurations can be predicted for various concentrations according to the ECI’s. An SQS represents a fully random alloy by means of a special configuration with a few (4~32) atoms to mimic the most relevant pair and multisite correlation functions of the solution[8-9]. SQS can be considered as a mixture of various microstates, i.e., an average structure for a given lattice. Hence, energy (also true for other properties) of SQS should be in the middle of the energy landscape of all microstates[10-11]. It is worth mentioning that the truncated error in determining ECI’s is unavoidable, making the CEM predicted low energy configurations less accurate[12]. In CEM, other approaches such as Monte Carlo[6]and the cluster variation method[13]need to be used to describe free energy at finite temperatures. SQS is only a special microstate, which cannot predict the expected low energy of disordered phase and handle its configurational entropy at finite temperatures. The shortcomings of SQS and CEM imply that new approaches for disordered phase are expected.

Recently we show that a macroscopically homogeneous single phase can be depicted as a statistical ensemble consisting of unique microstates with each possessing a distinguishable atomic, polar, magnetic, or other configuration[10, 14]. Consequently, an ordered phase is an ensemble dominated by one primary microstate, while a disordered phase possesses two and more types of noticeable microstates. The extension from the commonly used “phase” to a statistical ensemble of “microstates” is more or less a natural extension of the aforementioned CEM and SQS, and furthermore, the concept of the fluctuation of microstates opens an avenue to quantitatively tailor various macroscopic phenomena such as phase transition, Curie temperature, and anomalies of thermal expansion and heat capacity[10, 14], see details in Sections 2 and 3.

Understanding materials properties from microstates is also in line with the principle of statistic mechanics[15]: The microstates give more detailed information about the system, since the information needed to define a microstate is enough to allow one to calculate the corresponding macroscopic state but not vice versa. In addition, these microstates can be considered as the building blocks, i.e. the genome, of materials on the basis of the authors’ perspective[16]. In analogy to the genome concept in biologic systems, the “mutation” of materials genome can thus be viewed as the manifestation of statistic probability of various microstates. These “mutations” provide a theoretic foundation to understand materials properties, especially various anomalies such as colossally positive, zero, or negative thermal expansion, gigantic electrocaloric and electromechanical responses, anomalously low thermal conductivity, and spin distributions[10, 14, 16]. It is noted that each microstate possesses “normal” behaviors, while “anomalous” behaviors originate from the fluctuation of microstates, i.e., the microstate configurational entropy[14], see details in Section 2. Properties of interest for each microstate are therefore the foundation for the present partition function model. Relevant to thermodynamic properties at finite temperatures, the key is to determine phonon properties for each microstate. To this end, a parameter-free mixed-space approach[17], as implemented in the YPHON code[18], can be employed, which makes full use of the accurate force constants from the real-space supercell approach and the dipole-dipole interactions from the linear response theory in the reciprocal space. For polar materials, the mixed-space approach can adequately account for the long range dipole-dipole interactions which lead to the well-known LO-TO (longitudinal optical and transverse optical) splitting.

The present work aims to provide a perspective on the current advance of first-principles thermodynamics for both ordered and disordered phases. To this vision, the partition function approach in terms of a statistical ensemble of microstates is presented firstly in Section 2 for methodology. For each microstate, i.e., the ordered phase, the quasiharmonic approach to determine its thermodynamic properties is briefly discussed, where the vibrational contribution is accounted for using the YPHON code[17-18]for both polar and nonploar materials (microstates). In the Section 3 for results, examples are given for ordered phases of anti-fluorite Li2S, hcp Mg, and fcc Ni as well as disordered phases of Cu2ZnSnS4(CZTS) and fcc Ce. The associated anomalous properties for disordered phases are also presented and discussed in light of the fluctuation of microstates, i.e., the microstate configurational entropy.

2Methodology

Our perspective on first-principles thermodynamics is detailed here for both ordered and disordered phases, including the partition function approach in terms of microstates, the quasiharmonic approach for each microstate by means of phonon calculations, and the quasistatic approach for properties of interest at finite temperatures.

2.1Partition function approach in terms of microstates

As aforementioned, we recently went one step further than the commonly used “phase” to understand the origin as well as to quantitatively predict anomalous properties in nature. We propose that a macroscopically homogeneous single phase is a statistical ensemble composed of a number of unique “microstates” with each possessing a given atomic, polar, magnetic, or other configuration[10, 14, 19-22]. In terms of the conventional phase stability, the microstate with the lowest free energy is the stable state, and all others with higher free energies are metastable states[10, 14]. We postulate this competing system (single phase) belongs to a canonical ensemble under theNVTframework or a grand canonical ensemble under theμVTframework, whereNis the number of particles,Vis the volume,Tis the temperature, andμis the chemical potential. For example of aNVTensemble, the canonical partition function is,

(1)

whereZσrepresents the partition function of the individually distinguishable microstateσ,wσis the degeneracy factor (multiplicity) ofσ, β=1/(kBT) withkBthe Boltzmann constant, andFσis the Helmholtz energy ofσas a function ofVandT. The total Helmholtz energy of theNVTensemble is[14, 23-24],

(2)

wherexσ=Zσ/Zis the thermal probability of microstateσwith thewσincluded. Note that the value ofxσwithin a given ensemble is not random, but according to the free energy ofσ.SMCEis the microstate configurational entropy introduced automatically due to the competing stable and metastable microstates,

(3)

2.2Quasiharmonic approach for each microstate

As shown in Eqs. (1) and (2), the key to determine the total Helmholtz energy is the Helmholtz energy of each microstateσ, i.e., theFσ. Based on the quasiharmonic approach,Fσis usually represented by[2-3],

(4)

whereEσ(V) is the static energy at 0 K without the zero-point vibrational energy, determined by fitting the first-principles energy versus volume data points according to for example a four-parameter Birch-Murnaghan equation of state (EOS)[2],

Eσ(V)=a+bV-2/3+cV-4/3+dV-2

(5)

2.3Quasistatic approach for temperature-dependent properties

For properties that are mainly controlled by volume change with the increase of temperature, a quasistatic approach[35-36]can be used to predict the temperature-dependent properties in terms of the property-volume relationship from first-principles directly and the volume-temperature relationship from the quasiharmonic approach of Eq.(4) . According to this approach, elastic properties and direction-dependent thermal expansion coefficients have been predicted at finite temperatures for e.g. Al12Mg17[37], Mg2X(X=Si, Ge, Sn, and Pb)[38], Mg-La compounds[39], Al2O3[35], Ni-based superalloys[40], fcc-based metal nitrides[41], and cellulose[42]. Besides elasticity and thermal expansion, ideal shear strength and stacking fault energy were also predicted for fcc Ni at finite temperatures[43].

3Selected results and discussion

Five examples are shown in this Section to demonstrate the current advance of first-principles thermodynamics (see Sections 1 and 2) for both ordered phases (anti-fluorite Li2S, hcp Mg, and fcc Ni) and disordered phases (CZTS and fcc Ce). Since ordered phase can be depicted by one primary microstate, the normal first-principles calculations can be used. For disordered phase with two and more noticeable microstates, the partition function approach will be employed.

3.1Ordered phase containing one major microstate

Table 1　Calculated and experimental properties for anti-fluorite Li2S with space group , including the enthalpy of formation (ΔH, the reference states are-S and bcc Li[46], and the unit is kJ/mol-atom), the equilibrium volume (V0, Å3/atom), bulk modulus (B0, GPa) and its pressure derivative ), the band gap (BG, eV), and the Raman (R) and infrared (IR) phonon frequencies at the point (T2g and T1u modes with the unit of cm-1, and both the TO and LO modes are also shown for T1u)

Note:a SGTE (SSUB) data at 298 K estimated based on experimental results[52], b measured lattice parameter

a = 5.689 Å at 10 K[53],c based on c11= 95.4±3.5 and c12= 20.9±2.3 GPa via the measured acoustic phonons

at 15 K[53],d fitted results based on measured data at high pressures for reference only[54],e experimental data not

available, other predictions of indirect band gap from 3.14 to 4.55 eV[56],f measured at 18 K[55]

Fig.1　Calculated phonon dispersions and phonon density of state (PDOS) of anti-fluorite Li2S at its theoretical equilibrium volume in terms of PBEsol (see Table 1). Measured dispersions at 15 K by neutron scattering are also shown for comparison, including both the longitudinal (L) and transverse (T) polarizations [53]

Waals correction using the D3 method gives a better description of thermodynamic properties, agreeing with our previous findings for sulfur and sulfur-containing materials[46]. The example of Li2S indicates that (i) structural properties as well as electronic structures (e.g. band gap) can be predicted well in terms of a selected X-C functional, and (ii) phonon and associated thermodynamics can be predicted well using the YPHON code.

Fig.2　Calculated entropy (S) and heat capacity at constant pressure (Cp, p = 0 GPa) for anti-fluorite Li2S in terms of the quasiharmonic phonon approach and different X-C functionals. SGTE (SSUB) data are also shown for comparison [52]

The second example is Mg with hcp structure. Figure 3 shows the direction-dependent linear thermal expansion coefficients and the isothermal and isentropic elastic constants cij’s of hcp Mg[57]. These results were predicted based on the aforementioned quasistatic approach (see Section 2.3) and agree reasonably well experimental data[57]. Also based on the quasistatic approach, Figure 4 shows the third example: computed ideal shear strength of fcc Ni under both the pure alias and the pure affine shear deformations (see details in[43]). These two examples (hcp Mg and fcc Ni) indicate that the quasistatic approach is an effective but simple approach to predict properties at finite temperatures.

Fig.3　Predicted linear thermal expansion coefficients (LTE) along the a- and c-axis directions of hcp Mg and the isentropic and isothermal elastic constants cij’s of hcp Mg in terms of the quasistatic approach. Details of first-principles methodology and references for experimental data (the symbols) are given in the literature [57]

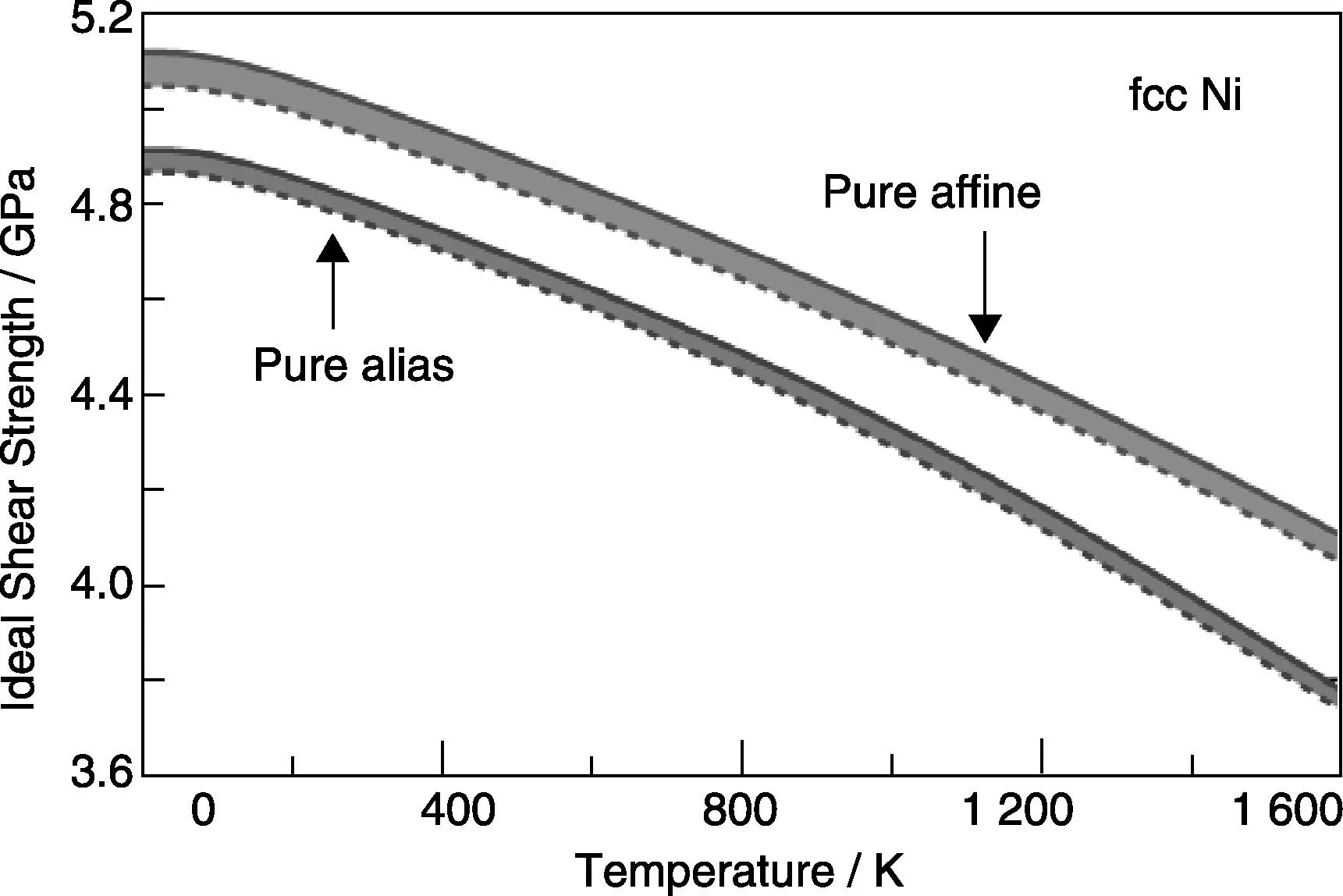
Fig.4　Predicted ideal shear strength of fcc Ni in terms of the quasistatic approach. Details of first-principles methodology and shear schemes (pure affine and pure alias shear deformations) are given in the literature[43]

For ordered phase with one major microstate, the examples of Li2S, hcp Mg, and fcc Ni as well as the ones mentioned in Section 2 indicate that first-principles is emerging as a routine technique to predict properties at finite temperatures in terms of a selected X-C functional and a proper methodology,for example the mixing-space approach, the quasiharmonic approach, and/or the quasistatic approach.

3.2Disordered phase containing more microstates

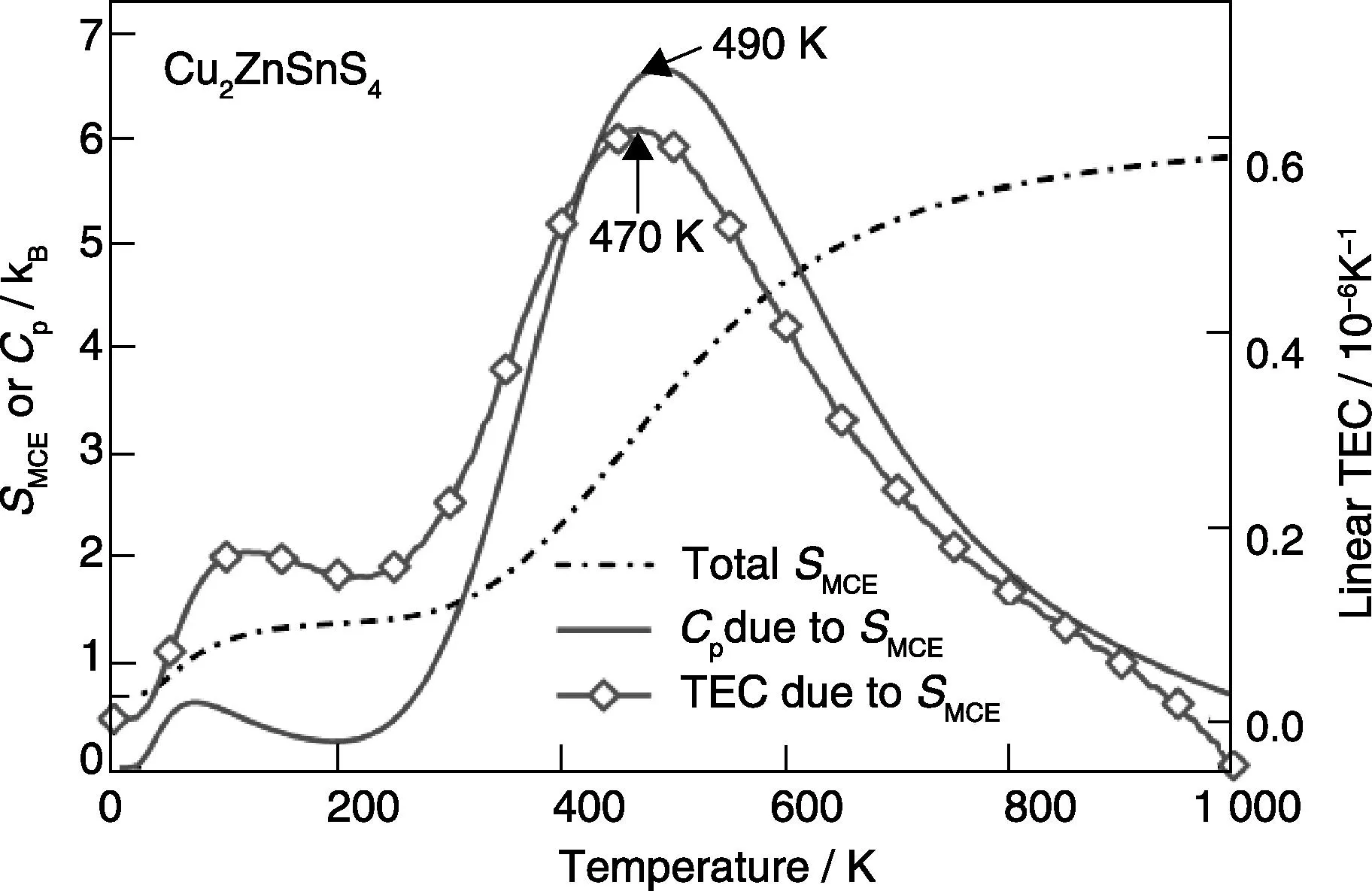
Fig.5　Calculated total microstate configurational entropy SMCE and associated heat capacity at constant pressure (Cp, p= 0 GPa) and linear thermal expansion coefficients (TEC) in terms of the 64-atom supercell of Cu2ZnSnS4 (CZTS). Details of first-principles methodology can be found in the literature[10]

The second example is a magnetic element fcc Ce, which possesses a colossal positive thermal expansion (CPTE) due to phase transition from the nonmagetic (NM) phase to the ferromagnetic (FM) phase with increasing temperature. Using the canonical partition function in terms of three magnetic microstates of the grand FM state and the metastable NM and antiferromagnetic (AFM) states[21, 24], the predicted miscibility gap and isobaric volumes at five pressures are plotted in Figure 6 as a function of temperature. Available experimental data are also included, agreeing well with the predictions, see details in [14]. Figure 6 shows that fcc Ce belongs to a single-phase region at all temperatures considered in the pressure range of 2.25~3.5 GPa. In this pressure range, normal thermal expansion is expected at both the low and high temperatures on each isobaric curve[14]. However in the middle temperature range on each isobaric curve (highlighted by the open diamond symbols), CPTE exists due to the fast increase of thermal probability of the metastable microstates with respect to temperature, see especially the curve with the pressure of 2.25 GPa, representing the critical point.

Fig.6　Isobaric volumes of fcc Ce at five pressures. The volume (V) is normalized to its equilibrium volume (VN) at stand pressure and temperature. The predicted CPTE regions are shown by the gray open diamonds, and the light gray open circle indicates the critical point. Details of first-principles methodology and references for experimental data (symbols except for the gray open diamonds) are given in the literature [14, 21, 24]

For disordered phase containing two and more microstates, the examples of CZTS, fcc Ce, and the aforementioned ones indicate that the (grand) canonical partition function can be used to quantitatively tailor disordered phase and associated anomalous properties. In practice, the ensemble can be selected based on crystallographic unit cell or its supercell, and all microstates within this ensemble should be accounted for in order to satisfy the condition of ergodicity in statistical physics. For example of a binary bcc phase, a 2×2×2 supercell with 16 atomic sites possesses 216= 65,536 microstates, but only 331 of them are independent. These independent microstates and the associated degeneracy factors can be generated using e.g. thegenstrcode (updated by the present author YW) within the ATAT package[60]. In principle, the larger the supercell/ensemble, the more accurate the results will be obtained. The amount of microstates around thousand is within the current capability of first-principle calculations. Based on our studies of CZTS[10], bcc Fe[19], and fcc Ni[25], fcc Ce[21, 24], Fe3Pt[20], and BeFe2As2[22], a supercell/ensemble with 16 or less atomic sites for disordered atoms, resulting in hundreds or less independent microstates for binary system, is big enough to study the properties of interest. In addition, an integrated first-principles, CEM, and partition function approach can be applied to study an ensemble using larger supercells. Note also that only the macroscopically homogeneous single phase for a given material is the present focus since the partition function approach is faced to phase consisting of microstates.

4Summary

The present work provide a perspective on the macroscopically homogeneous single “phase”, which can be depicted as a statistical ensemble consisting of one primary microstate (i.e., the ordered phase) or more noticeable microstates (i.e., the disordered phase). A DFT-based canonical (or grand canonical) partition function in terms of microstates is emerging as a key approach to describe disordered phase and associated anomalous properties. For a given microstate, the quasiharmonic approach in terms of first-principles phonon calculations is able to predict its thermodynamic properties. In addition, a quasistatic approach can be used to depict properties of interest at finite temperatures, such as elasticity, stacking fault, and ideal strength. It is shown that (i) the description of a macroscopically homogeneous “phase” in terms of “microstate(s)” opens a new pathway to quantitatively tailor anomalous properties such as thermal expansion and heat capacity, which are traceable from the microstate configurational entropy, and (ii) these microstates can be considered as the building blocks, i.e., the genome, of materials. Examples in the present work are given for the ordered phases of anti-fluorite Li2S, hcp Mg, and fcc Ni as well as the disordered phases of Cu2ZnSnS4(CZTS) and fcc Ce in order to demonstrate the current advance of first-principles thermodynamics at finite temperatures.

AcknowledgementsThis work was financially supported by the U.S. national science foundation (NSF) with Grant Nos. DMR-1006557, CHE-1230929, DMR-1310289, and CMMI-1333999. First-principles calculations were carried out partially on the LION clusters at the Pennsylvania State University, partially on the resources of NERSC supported by the Office of Science of the U.S. Department of Energy under contract No. DE-AC02-05CH11231, and partially on the resources of XSEDE supported by NSF with Grant No. ACI-1053575.

References

[1]Liu Z K. First-Principles Calculations and CALPHAD Modeling of Thermodynamics [J].JPhaseEquilibDiff, 2009, 30: 517-534.

[2]Shang S L, Wang Y, Kim D,etal. First-Principles Thermodynamics from Phonon and Debye Model: Application to Ni and Ni3Al [J].ComputMaterSci, 2010, 47: 1 040-1 048.

[3]Wang Y, Liu Z K, Chen L Q. Thermodynamic Properties of Al, Ni, NiAl, and Ni3Al from First-Principles Calculations [J].ActaMater, 2004, 52: 2 665-2 671.

[4]Shang S L, Wang Y, Kim D E,etal. Structural, Vibrational, and Thermodynamic Properties of Ordered and Disordered Ni1-xPtxAlloys from First-Principles Calculations [J].PhysRevB, 2011, 83: 144 204.

[5]Connolly J W D, Williams A R. Density-Functional Theory Applied to Phase Transformations in Transition-Metal alloys [J].PhysRevB, 1983, 27: 5 169-5 172.

[6]Van de Walle A, Ceder G. Automating First-Principles Phase Diagram Calculations [J].JPhaseEquilib, 2002, 23: 348-359.

[7]Van De Walle A. A Complete Representation of Structure-Property Relationships in Crystals [J].NatureMater, 2008, 7: 455-458.

[8]Zunger A, Wei S H, Ferreira L G,etal. Special Quasirandom Structures [J].PhysRevLett, 1990, 65: 353-356.

[9]Jiang C, Wolverton C, Sofo J,etal. First-Principles Study of Binary bcc Alloys Using Special Quasirandom Structures [J].PhysRevB, 2004, 69: 214202.

[10]Shang S L, Wang Y, Lindwall G,etal. Cation Disorder Regulation by Microstate Configurational Entropy in Photovoltaic Absorber Materials Cu2ZnSn(S,Se)4[J].JPhysChemC, 2014, 118: 24 884-24 889.

[11]Shang S, Wang Y, Wang W Y,etal. Low Energy Structures of Lithium-Ion Battery Materials Li(MnxNixCo1-2x)O2Revealed by First-Principles Calculations [J].ApplPhysLett, 2013, 103: 053 903.

[12]Shang S L, Wang Y, Du Y,etal. Entropy Favored Ordering: Phase Stability of Ni3Pt Revisited by First-Principles [J].Intermetallics, 2010, 18: 961-964.

[13]Shang S, Bottger A. A Combined Cluster Variation Method and Ab Initio Approach to the Gamma-Fe[N]/Gamma'-Fe4N1-xPhase Equilibrium [J].ActaMater, 2005, 53: 255-264.

[14]Liu Z K, Wang Y, Shang S. Thermal Expansion Anomaly Regulated by Entropy [J].SciRep, 2014, 4: 7 043.

[15]Garrod C.StatisticalMechanicsandThermodynamics[M]. New York:Oxford University Press, 1995.

[16]Liu Z K. Perspective on Materials Genome®[J].ChineseScienceBulletin, 2014, 59: 1 619-1 623.

[17]Wang Y, Wang J J, Wang W Y,etal. A Mixed-Space Approach to First-Principles Calculations of Phonon Frequencies for Polar Materials [J].JPhys-CondensMatter, 2010, 22: 202 201.

[18]Wang Y, Chen L Q, Liu Z K. YPHON: A Package for Calculating Phonons of Polar Materials [J].ComputPhysCommun, 2014, 185: 2 950-2 968.

[19]Shang S L, Wang Y, Liu Z K. Thermodynamic Fluctuations Between Magnetic States from First-Principles Phonon Calculations: The Case of bcc Fe [J].PhysRevB, 2010, 82: 014 425.

[20]Wang Y, Shang S L, Zhang H,etal. Thermodynamic Fluctuations in Magnetic States: Fe3Pt as a Prototype [J].PhilosMagLett, 2010, 90: 851-859.

[21]Wang Y, Hector L G, Zhang H,etal. A Thermodynamic Framework for a System with Itinerant-Electron Magnetism [J].JPhys-CondensMatter, 2009, 21: 326 003.

[22]Wang Y, Shang S L, Chen L Q,etal. Magnetic Excitation and Thermodynamics of BaFe2As2[J].InterJQuanChem, 2011, 111: 3 565-3 570.

[23]Sadus R J.MolecularSimulationofFluids:Theory,AlgorithmsandObject-orientation[M].Amsterdam:Elsevier, 1999.

[24]Wang Y, Hector L G, Zhang H,etal. Thermodynamics of the Ce Gamma-Alpha Transition: Density-Functional Study [J].PhysRevB, 2008, 78: 104 113.

[25]Shang S L, Saal J E, Mei Z G,etal. Magnetic Thermodynamics of fcc Ni from First-Principles Partition Function Approach [J].JApplPhys, 2010, 108: 123 514.

[26]Shang S L, Wang Y, Mei Z G,etal. Lattice Dynamics, Thermodynamics, and Bonding Strength of Lithium-Ion Battery Materials LiMPO4(M = Mn, Fe, Co, and Ni): A Comparative First-Principles Study [J].JMaterChem, 2012, 22: 1 142-1 149.

[27]Shang S L, Hector L G, Shi S Q,etal. Lattice Dynamics, Thermodynamics and Elastic Properties of Monoclinic Li2CO3from Density Functional Theory [J].ActaMater, 2012, 60: 5 204-5 216.

[28]Mei Z G, Wang Y, Shang S L,etal. First-Principles Study of Lattice Dynamics and Thermodynamics of TiO2Polymorphs [J].InorgChem, 2011, 50: 6 996-7 003.

[29]Wang Y, Fang H, Zacherl C L,etal. First-Principles Lattice Dynamics, Thermodynamics, and Elasticity of Cr2O3[J].SurfSci, 2012, 606: 1 422-1 425.

[30]Wang Y, Saal J E, Wang J J,etal. Broken Symmetry, Strong Correlation, and Splitting between Longitudinal and Transverse Optical Phonons of MnO and NiO from First Principles [J].PhysRevB, 2010, 82: 081 104.

[31]Wang Y, Saal J E, Mei Z G,etal. A First-Principles Scheme to Phonons of High Temperature Phase: No Imaginary Modes for Cubic SrTiO3[J].ApplPhysLett, 2010, 97: 162 907.

[32]Wang Y, Saal J E, Wu P P,etal. First-Principles Lattice Dynamics and Heat Capacity of BiFeO3[J].ActaMater, 2011, 59: 4 229-4 234.

[33]Wang Y, Wang J J, Saal J E,etal. Phonon Dispersion in Sr2RuO4Studied by a First-Principles Cumulative Force-Constant Approach [J].PhysRevB, 2010, 82: 172 503.

[34]Wang Y, Zhang L A, Shang S,etal. Accurate Calculations of Phonon Dispersion in CaF2and CeO2[J].PhysRevB, 2013, 88: 024 304.

[35]Shang S L, Zhang H, Wang Y,etal. Temperature-Dependent Elastic Stiffness Constants of Alpha- and Theta-Al2O3from First-Principles Calculations [J].JPhys-CondensMatter, 2010, 22: 375 403.

[36]Wang Y, Wang J J, Zhang H,etal. A First-Principles Approach to Finite Temperature Elastic Constants [J].JPhys-CondensMatter, 2010, 22: 225 404.

[37]Zhang H, Shang S L, Wang Y,etal. First-Principles Calculations of the Elastic, Phonon and Thermodynamic Properties of Al12Mg17[J].ActaMater, 2010, 58: 4 012-4 018.

[38]Ganeshan S, Shang S L, Wang Y,etal. Temperature Dependent Elastic Coefficients of Mg2X(X= Si, Ge, Sn, Pb) Compounds from First-Principles Calculations [J].JAlloysCompd, 2010, 498: 191-198.

[39]Wrobel J, Hector L G, Wolf W,etal. Thermodynamic and Mechanical Properties of Lanthanum-Magnesium Phases from Density Functional Theory [J].JAlloysCompd, 2012, 512: 296-310.

[40]Shang S L, Kim D E, Zacherl C L,etal. Effects of Alloying Elements and Temperature on the Elastic Properties of Dilute Ni-Base Superalloys from First-Principles Calculations [J].JApplPhys, 2012, 112: 053 515.

[41]Wang A, Shang S L, He M,etal. Temperature-Dependent Elastic Stiffness Constants of fcc-Based Metal Nitrides from First-Principles Calculations [J].JournalofMaterialsScience, 2014, 49: 424-432.

[42]Dri F L, Shang S L, Hector L G,etal. Anisotropy and Temperature Dependence of Structural, Thermodynamic, and Elastic Properties of Crystalline Cellulose I-Beta: a First-Principles Investigation [J].ModellingSimulMaterSciEng, 2014, 22: 085 012.

[43]Shang S L, Wang W Y, Wang Y,etal. Temperature-Dependent Ideal Strength and Stacking Fault Energy of fcc Ni: A First-Principles Study of Shear Deformation [J].JPhys-CondensMatter, 2012, 24: 155 402.

[44]Kresse G, Furthmuller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set [J].PhysRevB, 1996, 54: 11 169-11 186.

[45]Kresse G, Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method [J].PhysRevB, 1999, 59: 1 758-1 775.

[46]Shang S L, Wang Y, Guan P W,etal. Insight into Structural, Elastic, Phonon, and Thermodynamic Properties of α-Sulfur and Energy-Related Sulfides: A Comprehensive First-Principles Study [J].JMaterChemA, 2015, 3: 8 002-8 014.

[47]Perdew J P, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple [J].PhysRevLett, 1996, 77: 3 865-3 868.

[48]Perdew J P, Ruzsinszky A, Csonka G I,etal. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces [J].PhysRevLett, 2008, 100: 136 406.

[49]Grimme S, Antony J, Ehrlich S,etal. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu [J].JChemPhys, 2010, 132: 154 104.

[50]Heyd J, Scuseria G E, Ernzerhof M. Hybrid Functionals Based on a Screened Coulomb Potential [J].JChemPhys, 2003, 118: 8 207-8 215.

[51]Blöchl P E, Jepsen O, Andersen O K. Improved Tetrahedron Method for Brillouin-Zone Integrations [J].PhysRevB, 1994, 49: 16 223-16 233.

[52]Scientific Group Thermodata Europe (SGTE), ed.ThermodynamicPropertiesofInorganicMaterials[M].Berlin:Springer,1999.

[53]Buehrer W, Altorfer F, Mesot J,etal. Lattice-Dynamics and the Diffuse Phase-Transition of Lithium Sulfide Investigated by Coherent Neutron-Scattering [J].JPhys-CondenMatter, 1991, 3: 1 055-1 064.

[54]Grzechnik A, Vegas A, Syassen K,etal. Reversible Antifluorite to Anticotunnite Phase Transition in Li2S at High Pressures [J].JSolidStateChem, 2000, 154: 603-611.

[55]Bertheville B, Bill H, Hagemann H. Experimental Raman Scattering Investigation of Phonon Anharmonicity Effects in Li2S [J].JPhysCondensMatter, 1998, 10: 2 155-2 169.

[56]Khachai H, Khenata R, Bouhemadou A,etal. FP-APW + LO Calculations of the Electronic and Optical Properties of Alkali Metal Sulfides under Pressure [J].JPhys-CondenMatter, 2009, 21: 095 404.

[57]Shang S L, Liu Z K.ThermodynamicPropertiesofMagnesiumAlloys,inFundamentalsofMagnesiumAlloyMetallurgy[M].Cambridge:Woodheed Publishing,2013,85-124.

[58]Scragg J J S, Choubrac L, Lafond A,etal. A Low-Temperature Order-Disorder Transition in Cu2ZnSnS4Thin Films [J].ApplPhysLett, 2014, 104: 041 911.

[59]Schorr S, Gonzalez-Aviles G. In-Situ Investigation of the Structural Phase Transition in Kesterite [J].PhysStatusSolidiA, 2009, 206: 1 054-1 058.

[60]Van De Walle A, Tiwary P, De Jong M,etal. Efficient Stochastic Generation of Special Quasirandom Structures [J].Calphad, 2013, 42: 13-18.

(编辑盖少飞惠琼)

First-Principles Thermodynamics at Finite Temperatures:Perspective on Ordered and Disordered Phases

Shunli SHANG, Yi WANG, Zi-kui LIU

(Department of Materials Science and Engineering, The Pennsylvania State University,

University Park, Pennsylvania 16802, USA)

Abstract：A longstanding issue of first-principles calculations is to predict thermodynamic properties for a disordered phase at finite temperatures. Here, we show that a recent advance for this issue is the partition function approach in terms of microstates, which is the key for both ordered phase with one primary microstate and disordered phase consisting of two and more noticeable microstates. For a given microstate, first-principles phonon calculations in terms of the quasiharmonic approach provide a practical pathway to predict its thermodynamic properties. In the present paper, a summary of properties predicted at finite temperatures is presented, and examples are given for ordered phases of anti-fluorite Li2S, hcp Mg, and fcc Ni as well as disordered phases of Cu2ZnSnS4(CZTS) and fcc Ce. It is shown that (i) the extension from “phase” to “microstate” opens an avenue to quantitatively tailor anomalous properties such as phase transition and thermal expansion anomaly, and these anomalies are traceable from the microstate configurational entropy, and (ii) these microstates can be considered as the building blocks, i.e., the genome, of materials.

Key words：first-principles phonon calculations； quasiharmonic approach； microstate； ordered phase； disordered phase； thermodynamic properties

DOI:10.7502/j.issn.1674-3962.2015.04.06