新型优化SIFT的图像快速配准方法研究

魏利胜 ，周圣文

1.安徽工程大学 电气工程学院，安徽 芜湖 241000

2.上海大学 机电工程与自动化学院，上海 200072

图像匹配是虚拟现实、机器视觉等领域的一个研究热点[1]，被广泛应用于远程监控、工业机器人、地质勘探、医疗诊断以及汽车电子等领域[2]。它主要包括图像配准和图像融合两个方面。当前，许多科研人员对图像配准技术及应用进行了深入研究，取得了丰硕的成果。

Lowe[3]于1999年提出了尺度不变特征变换（Scale Invariant Feature Transform，SIFT）图像配准算法，该方法在仿射、旋转、缩放、遮蔽、光照等方面均具有较好的不变性，其配准精度高，而得到广泛应用；张凯等[4]将SIFT算法运用于智能对靶施药系统中的图像特征匹配，实现高噪声环境下的红掌图像快速有效的拼接；傅卫平等[5]利用SIFT算法进行图像初次匹配，并计算出仿射变换的参数，以推导出复杂环境中图像目标的形心位置及其坐标定位；在文献[6]中，朱梅华等将SIFT算法用于处理卷烟小包装的图像配准中，取得了良好的效果。然而，传统SIFT算法耗时较长，导致其在实时性要求较高的应用场合受到制约[2，7]。因此，如何提高SIFT算法的实时性已成为国内外学者的探索焦点[8-14]。李芳芳等[8]通过自适应选择高斯核函数的尺寸大小，并通过构建三角网法进行小面元微分纠正配准，以提高SIFT算法的实时性；张谦等[9]利用均匀网格分割图像，以网格数量及其局部区域熵来决定特征点数量、分布，并在此基础上采用放射变换进行特征匹配，以达到配准效率高和实时性好的目的；在文献[10]中，熊自明等将SIFT算法和Harris特征点进行结合，以Harris特征点作为待匹配特征点，并利用主成分分析法（Principle Component Analysis，PCA）得到降维后的特征向量，大大提升了SIFT算法的配准效率；王民等在文献[11]中采用DOG尺度空间提取Harris算子作为图像的特征点，提出了一种基于Harris角点的SIFT立体匹配方法；Sukthankar等[12]也通过PCA法将特征向量维数由128维降到20维，以提升原算法实时性；赵垒等[13]以特征圆环领域代替方形区域进行特征向量计算并进行排序，省去特征点主方向计算，减少了特征描述符维数；另外，王田甲等[14]提出了一种在方形邻域内提取60维描述子的SIFT匹配算法，Bay使用近似Hessian矩阵进行关键点提取，同时引入haar小波变换进行特征方向以及特征描述符计算，生成64维特征向量，以提升算法的匹配效率和准确性。

以上文献主要集中于SIFT算法特征点的提取以及后续匹配算法的改进，并取得了一定的成果。本文将在以上研究基础上，通过极值特性约束条件和降采样预处理，利用差分尺度空间的局部单极值，实现重合区域特征提取和匹配，以减小冗余特征点，从而有效提高匹配速度和配准精度。

1 重合区极值特征提取法

图像配准的过程主要包括图像特征点的提取、匹配以及坐标变换三个环节[15]，即：利用SIFT算法来提取图像特征点，生成特征向量；然后，利用最近邻次近邻欧式距离之比进行粗匹配；再进一步采用RANSAC算法进行精匹配，计算得到图像拼接变换矩阵H；最后，使用变换矩阵H将待配准的两幅图像变换在同一坐标系下进行图像匹配。SIFT算法实时性、精确度在很大程度上受特征点对数量的影响，且特征点粗匹配的精确率直接影响RANSAC算法抽样次数。为此，本文在特征匹配的过程中，只考虑重叠区域的特征点对，从而剔除重叠区域以外的特征点对，以减小图像配准过程中的无用计算和错误匹配。

考虑到图像匹配点对极值具有一致性的特点，即同为极大值或同为极小值[16]，而传统SIFT算法并未考虑该约束条件，对极大和极小值组成的特征集均进行搜索匹配，会增大图像误匹配率和匹配时间。假设特征点集A极大值点和极小值点分别为m、n，特征点集B中分别为m′、n′。若采用穷举搜索的话，搜索次数为：

而利用极值约束条件后，极大值只在极大值之间进行搜索，极小值同理，搜索次数变为：

仅选择极大值或极小值时作为特征点时，搜索次数则为：

由式（1）～（3）得到k2＜k1＜k，可见，极值约束条件下能够有效降低搜索次数，若仅选择一种极值点作为特征点不仅能够降低特征提取数量，从而减少特征提取过程耗时，且可以有效减少搜索次数；另外，传统SIFT算法是在极大和极小值所组成的特征集中进行搜索匹配，会造成误匹配率的增加，因此利用重合区单极值作为待匹配特征点，将大大减少冗余特征点对数量，可有效提高SIFT算法的实时性以及匹配率。

2 图像降采样预处理法

针对传统SIFT算法实时性差的问题，本章将进一步采用图像有下限降采样预处理方法，以缩小图像尺寸，并根据拍摄设备位置关联性这一约束条件估计出图像重合区域；然后依据极大值特征点对提取法，减少特征点对的数量；最后，通过计算未缩放前原始图像变换矩阵H与降采样后的变换矩阵H1之间的关联性，将原始图像变换同一坐标系下完成原图像配准工作，以提高SIFT算法的实时性。其流程图如图1所示。

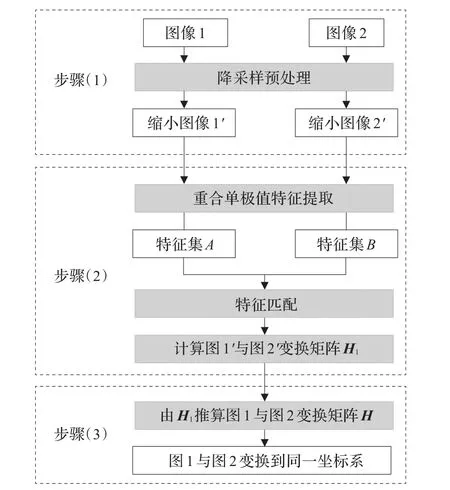
图1 改进SIFT算法配准流程图

图1中的改进SIFT算法配准流程主要包括三个部分：（1）有下限降采样过程；（2）重合区极大值提取法，利用该方法提取图像特征并匹配，得到缩小后图像变换矩阵H1；（3）根据变换矩阵之间的关联性，推导原始图像之间坐标变换，实现原始图像配准。

2.1 图像降采样预处理

原SIFT算法通过寻找待配准图像间的匹配特征点对实现图像变换矩阵H的求解，以完成图像配准[16]。设 (x，y)(，)是原图像的一对匹配特征点对，其变换矩阵H如式（4）所示：

可见至少需要四对正确的匹配特征点对才能完成变换矩阵H相关参数的求解。通常情况下大尺度图像会产生大量冗余特征点以及匹配点对数量，使得图像配准所用时间大大增加。文献[17]通过对图像进行降采样预处理，对不同采样倍数和不同插值方法进行对比，发现图像降采样80%～90%时，能满足匹配的精度和匹配点对数量，并相对原算法减少了20%～30%的配准时间。因此，本文将在文献[17]的基础上，以尺寸（180×180）为限对原图像进行三次卷积内插降采样预处理，并保持待配准图像之间降采样比例相同，有效减少冗余特征点以提升图像配准的实时性。为此，需要先计算出降采样后图像的变换矩阵H1与原始图像间的变换矩阵H之间的关联性。

2.2 变换矩阵之间关联性

图像进行降采样预处理之后，特征提取及匹配均是在缩小后的图像上进行，因此式（6）图像之间变换矩阵H1是缩小后图像之间的变换矩阵。若直接采用缩小后的图像进行配准，会严重影响图像的分辨率。为此，需要求取原始图像之间的变换矩阵H和预处理后的变换矩阵H1之间的关联性。本文通过计算出缩放后图像之间的变换矩阵，然后利用缩放系数，以推导出缩放前后图像两变换矩阵之间的关系，从而得到原图像之间的变换矩阵，以实现图像之间坐标变换。

设两待配准图像大小分别为 (m，n)、(k，l)，则降采样比例p和变换矩阵H1如下所示：

可见：

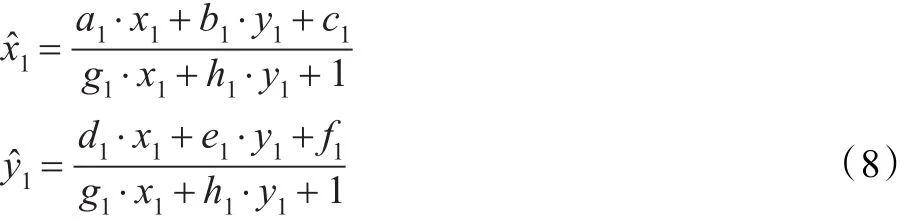
由上式可得：

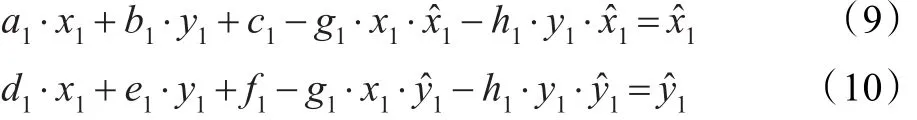
根据原图像的一对匹配特征点对变换矩阵H，可知：

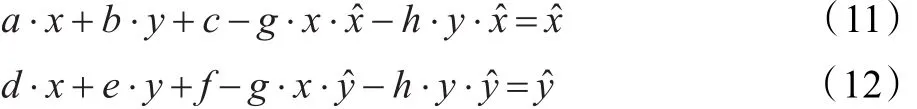
将式（13）～（14）代入式（9）～（10）并化简，可知：

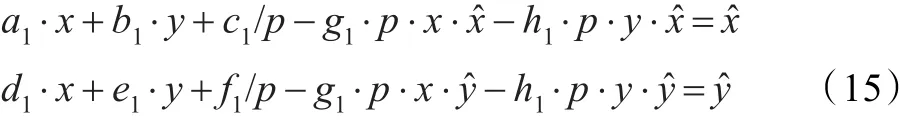
根据式（15）和式（11）～（12）可以得到：

可见，根据式（16）可以推导降采样图像的变换矩阵H1与原始图像间的变换矩阵H之间的变换关系，从而实现原始图像间的配准，减少图像匹配的时间。

3 实验验证

本实验平台为Window XP操作系统，CPU为3.3 GHz，内存2 GB，编程环境Matlab 7.0，原始图像大小为768×1 280，如图2所示，其中图（a）为左镜头拍摄的图像，而图（b）为右镜头拍摄图像。下面将重点探讨如何基于优化SIFT方法对两幅图像进行拼接实验。

图2 配准图像

实验1基于重合区极大值特征提取法

为了能够明确改进方法与传统SIFT特征提取的效率，选择SIFT特征提取时间、粗匹配率以及精匹配率三个指标进行对比，如下：

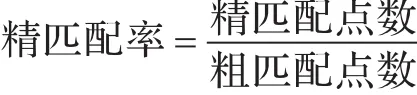
利用实验可得传统SIFT算法特征点分布以及改进的重合区极大值特征分布图如3所示。

图3 图像特征点提取分布图

图3（a）表示传统SIFT算法提取特征点分布结果，图3（b）表示改进的基于重合区极大值提取特征点分布结果，红色代表所提取的特征点，可见，改进后的图像特征点数量得到了明显的降低。

由表1可知，经过选取图像重合区域后，在重合区域采用图像极大值（或极小值）作为图像特征点，能有效去除无效特征点数量，特征点数缩小约75%，且粗匹配与精匹配准确率均得到大幅度提高，其中粗匹配率提高20.9%，精匹配率提高34.7%，总共匹配用时由103.516 s缩减到13.515 s，可见改进方法大幅度缩减了时间消耗，提高了图像匹配的实时性。经过配准后，得到的拼接效果如图4所示。

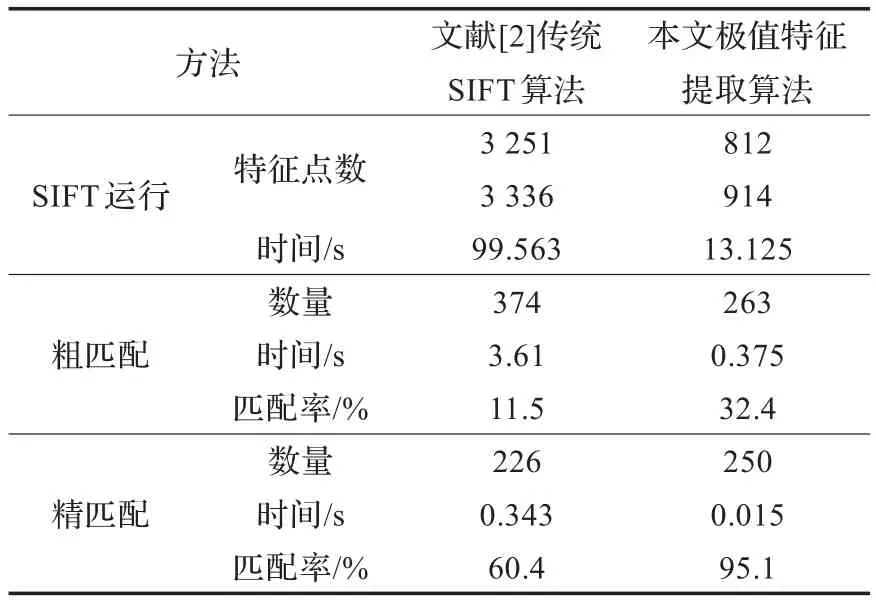
表1 实验数据分析表

实验2降采样预处理配准法

为了进一步验证降采样预处理方法的有效性，先将图像尺寸缩小，通过式（4）、（6）以及（16）之间的关联性，对原始图像进行拼接实验，其提取的特征点分布结果如图5所示。

从图5中可知，采用降采样预处理配准法后，图像的特征点数量得到了进一步的降低。

图4 拼接效果图

图5 降采样预处理特征点提取分布图

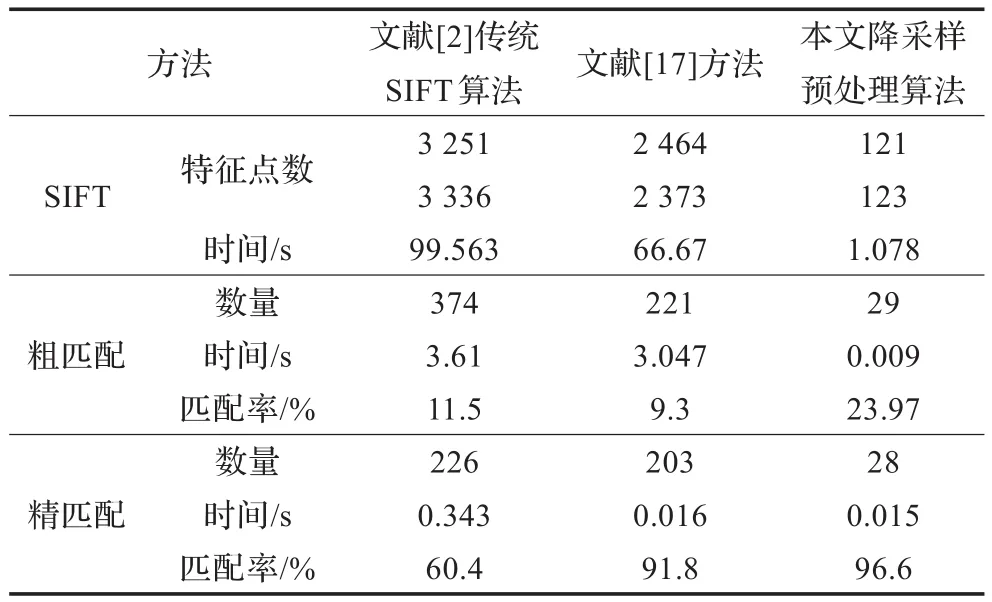
表2 实验数据分析表

由表2可知，基于图像尺寸降采样预处理，能进一步去除无效特征点数量，减少冗余特征点，特征点数由传统SIFT算法的3 251个降低为121个，其粗匹配率由11.5%提高到23.97%、精匹配率由60.4%提高到96.6%，总共匹配用时由103.516 s缩减到1.102 s，可见改进后的图像匹配方法能大幅度缩减时间消耗，提高了图像匹配的实时性以及配准精度。

经过配准后，得到的拼接效果如图6所示，其中（a）表示采用传统SIFT算法拼接的效果图，（b）表示采用文献[17]的降采样算法拼接的效果图，（c）表示采用降采样+重合区极大值优化方法拼接的效果图。

4 结束语

本文在对传统SIFT图像拼接算法相关理论研究基础上，提出了两种改进的SIFT算法，首先，通过寻找重叠区的策略来降低特征点对的数量，从而有效减少了原SIFT算法的复杂度和配准时间；在此基础上，采用极大值匹配方法和图像降采样预处理方法，以有效消除重复和错误匹配。实验结果表明本文所提算法比传统SIFT算法在图像配准中取得了更高的配准速度和精度。

图6 拼接效果图

[1]吕娜，冯祖仁.图像匹配与跟踪研究[J].西安交通大学学报，2010，44（10）.

[2]白廷柱，侯喜报.基于SIFT算子的图像匹配算法研究[J].北京理工大学学报，2013，33（6）：622-627.

[3]Qi Zhi，Cooperstock J R.Toward dynamic image mosaic generation with robustness to parallax[J].IEEE Transactions on Image Processing，2012，21（1）：366-378.

[4]张凯，耿长兴，张二鹏，等.温室环境下红掌图像拼接算法[J].农业机械学报，2013，44（4）：223-227.

[5]傅卫平，秦川，刘佳，等.基于SIFT算法的图像目标匹配与定位[J].仪器仪表学报，2011，32（1）：163-169.

[6]朱梅华，魏承科，张素伟.SIFT算法在卷烟小包装图像配准中的应用[J].计算机工程与应用，2012，48（21）：244-248.

[7]Kim B S，Lee S H，Cho N I.Real-time panorama canvas ofnaturalimages[J].IEEE Transactions on Consumer Electronics，2011，57（4）：1961-1968.

[8]李芳芳，肖本林，贾永红，等.算法优化及其用于遥感影像自动配准[J].武汉大学学报，2009，34（10）：1245-1249.

[9]张谦，贾永红，胡忠文.遥感影像配准中的SIFT特征匹配改进[J].微电子学与计算机，2013，38（4）：455-459.

[10]熊自明，万刚，闫鹤，等.SIFT算法的小型无人机航拍图像自动配准[J].绘测科学技术学报，2012，29（2）：153-156.

[11]王民，刘伟光.基于改进SIFT特征的双目图像匹配算法[J].计算机工程与应用，2013，49（2）：203-206.

[12]Ke Y，Sukthankar R.PCA-SIFT：a more distinctive representation for local image descriptors[C]//Proceedings of the Conference on Computer Vision and Pattern Recognition，Washington，USA，2004：511-517.

[13]赵垒，侯振杰.一种改进的SIFT图像配准方法[J].计算机工程，2012，36（12）：226-228.

[14]王田甲，刘国荣.SIFT改进算法在图像配准中的应用[J].微电子学与计算机，2011，28（5）：184-188.

[15]刘健，张国华，黄琳琳.基于改进SIFT的图像配准算法[J].北京航空航天大学学报，2010，36（9）：1121-1124.

[16]Zhou Wu，Goshtasby A.Adaptive image registration via hierarchical voronoi subdivision[J].IEEE Transactions on Image Processing，2012，21（5）：2464-2473.

[17]王书民，张爱武，崔营营.基于降采样处理的低空遥感影像SIFT特征匹配分析[J].测绘通报，2011（9）：18-20.