普通光照下叶片图像特征信息抽取

赵 方，石 晟，闫 民

1.北京林业大学 信息学院，北京 100083

2.北京林业大学 工学院，北京 100083

1 引言

农林业随着现代信息技术的发展已经进入信息化时代，随着精准农业，精准林业的概念提出，针对传统林业作业的改造也在不断深入。传统林业外业进行标本采集费时费事，采集数字信息将成为趋势。对比于传统的粗放式管理模式，基于图像识别、机器视觉的新型叶片识别技术将大大提高作业的精细度、准确度，在使得资料更加完备和细致的同时，减少林业外业人员的工作负荷和知识要求，同时降低人为失误率。

真实拍摄的叶片即使采用纯色背景做垫衬，也会因为光照不均匀，摆放不平整等因素产生很多阴影干扰。此外，由于垫衬物的纹理以及细小痕迹也会对实际采集的叶片图像造成干扰，因此要切实进行实用的叶片识别系统开发，必须要能够处理掉这些光影和杂色干扰。文章中将先针对如何去除阴影及杂色干扰进行成果的介绍。

此外，对于同类树木的多个叶片，存在着具体形状及纹理上的偏差，因此不适用于确定形状的识别算法。且叶片本身所含有的信息量比较复杂，大体包括叶形、叶脉、叶边缘等信息，通常的识别算法只要抓住其中一组信息即可达到一定的识别率，但若要区分得更精细，需要提取尽可能多的叶片形态学特征，本文将就如何进行全面的叶片形态学特征抽取进行研究，并介绍其成果。

2 背景研究

国外自1986年开始研究如何利用图像特征对叶片进行分类，1986年Ingrouille和Laird利用27种叶形特征对橡树进行了分类[1]，Guye等人则通过拓扑不变量如伸长度、紧密度和中心惯性矩生长初期的植物进行了有效分类[2]，之后越来越多的研究人员对此课题进行了研究，用于辨别叶片所使用到的叶片图像特征包括形态学特征（包括紧密度、圆度、伸长度、叶状度等简单形状因子，叶片轮廓的曲率尺度空间计算而来的轮廓凹凸性等复杂统计特性，偏心率、圆形性、弯曲能量等拓扑不变量特性），色彩特征，植物学局部特征（叶脉走向，叶边缘的叶齿）以及通过对叶片图像进行小波变化后在频域检测其纹理特征等。采用的分类方法包含有k-NN（k-Nearest Neighbor）k近邻算法，ANN（Artificial Neuron Network）人工神经网络分类算法以及SVM（Support Vector Machine）支持向量机分类算法，这些分类算法普遍可以达到70%以上的识别正确率，在某些有特定分类的叶片识别方面，准确度可以更高。

国内的研究相对开展较晚，最早的研究开始于1994年，傅星等人对利用计算机进行植物分类开展了初步研究，达到了使用计算机对植物性状进行自动提取和分类的结果[3]。之后多名专家学者对这一问题从各种方面进行了研究，目前比较好的研究中记录的识别率可以达到80%以上。

基于叶片形态学进行的实验研究也在最近几年进展迅速，比较典型的如，国外Jyotismita Chaki和Ranjan Parekh从图像的矩不变特征（M-I）和中心半径（C-R）模型对叶片图像进行建模识别，得到了90%以上的识别率[4]，国内的侯铜，姚立红，阚江明等人利用叶片轮廓计算得到叶片的矩形度，圆形度，偏心率等几何特征和多个图像不变矩作为特征值，利用神经网络进行分类识别，也获得了92%的高识别率[5]。

目前的大部分叶片识别研究专注于无背景干扰的单一叶片识别，并未考虑光线复杂的情况下各类阴影及背景杂色的干扰，也只有少数研究考虑过在复杂背景中如何辨别并分隔出叶片。汤晓东等人的《复杂背景下的大豆叶片识别》[6]在研究叶片识别的时候考虑了在复杂背景下使用分水岭的迭代算法来提取叶片，使得辨识问题更加实用，但提取的叶片种类单一，无法做到任意叶片的提取。

文章将就在真实的光照条件下拍摄的，有轻微杂色干扰的任意叶片图像的识别算法进行研究。

3 算法设计及系统实现

本次实验中处理的图像，颜色存储方式为ARGB色彩，每个通道的色彩占据8位，图片格式为JPG。图片上的像素点采用通用的直角坐标系描述，以左上角点为原点，向下为Y正方向，向右为X正方向。

3.1 总体流程

如图1，其中椭圆形的节点表示数据，方形的节点表示处理的流程，算法针对图片数据进行，最终得到图像特征数据。其中灰色加重部分为本次实验未完成的一个流程。

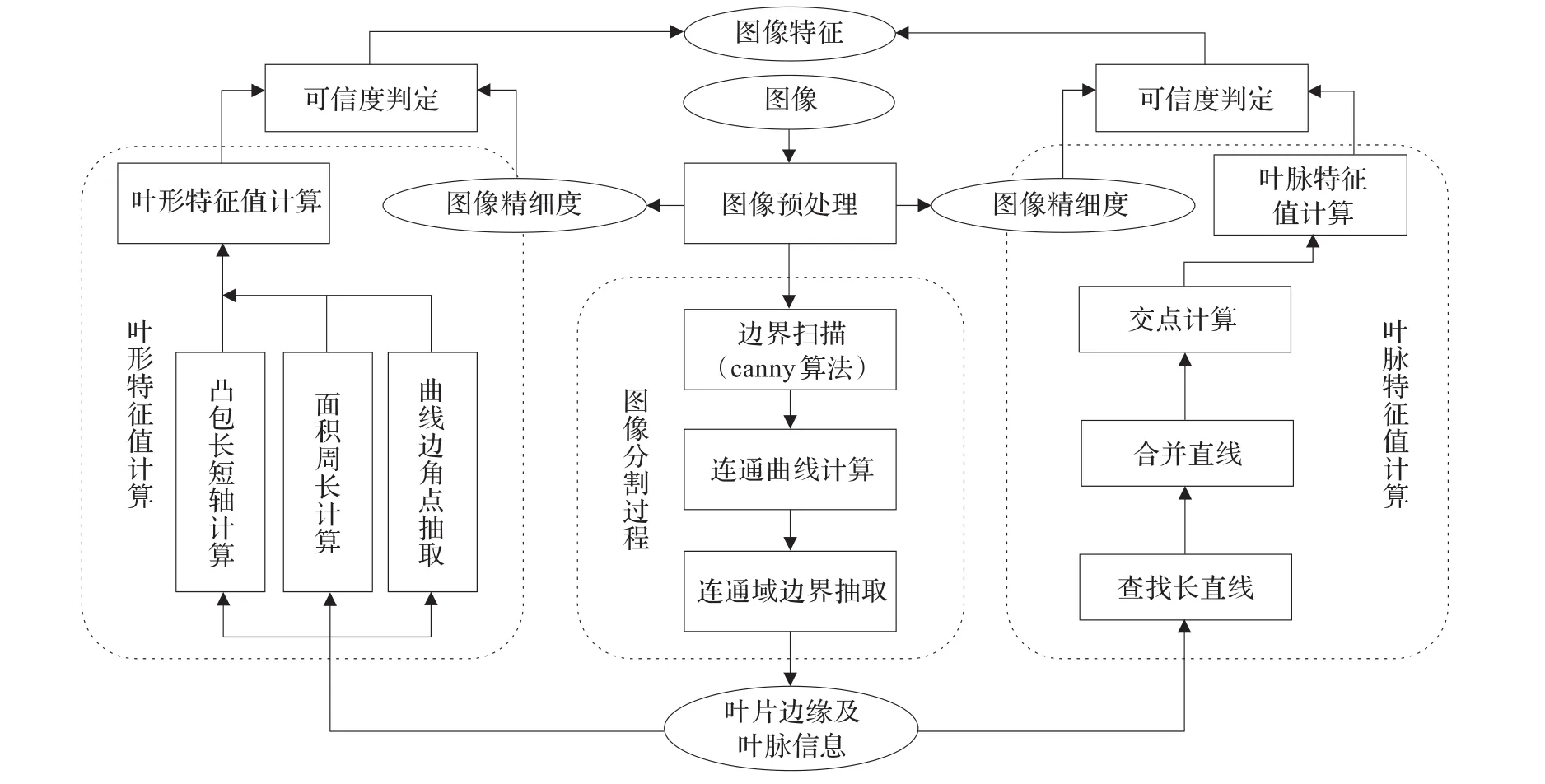
图1 叶片信息提取算法总体流程

整体叶片数据抽取的算法实现如图1，整套算法分为：图像预处理、图像分割、叶形特征值计算、叶脉特征值计算、可信度计算以上五部分流程组成，下面将就每一部分功能和相关算法进行详细介绍。

3.1.1 图像预处理

图像预处理的工作主要是为了两个方面：（1）去除杂色干扰；（2）评估图像的精细度。

由于叶片图像通常以绿色为主，故针对此信息，将原始图像的彩色数值按照绿色和非绿色进行区分，强化绿色分量，弱化其他分量，从而使得对比更加强烈，具体做法：

（1）记a为图像上坐标为(x，y)的像素点的色彩值。

（2）记r=(a&0x00FF0000)＞＞16，g=(a&0x0000FF00)＞＞8，b=a&0x000000FF，其中＞＞为按位右移运算符，&为按位与运算

（3）变换后图像对应(x，y)点上色彩值为a0=g＜＜16+b＜＜7+r＜＜3，其中＜＜为按位左移运算符。

可以由算法看出，经过这样处理后，得到的颜色数值，绿色分量得到了增强，原来包含绿色分量的色彩点的数值会变得很大，而不包含绿色分量的色彩，则由于蓝色和红色分量色彩均右移比左移多一位，故数值会变得更小。经过这样的处理后，可以确保图像有更大的区分度。

图像的精细度则用图像的长度w，图像的宽度h和空白像素数目e决定，图像精细度是为了确保图像中某些精细结构计算可以有意义，因为当图像过小的时候，图像的角点信息，以及叶脉细节信息会抽取出异常值。图像精细度r定义为0到1的小数，其值越小，精细度越差，其计算公式如下：

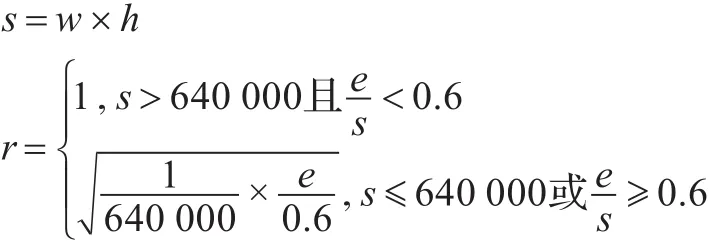
公式中w为图像长度，h为图像宽度（默认w≥h）。e为空白像素数目，空白像素数目在后续计算中可以得到，图像面积s减去叶片面积即为空白像素数目。

预处理过程中，也会计算图像的各种相关参数，以便于后续使用。

3.1.2 图像分割

图像分割的目的也有两个：（1）分割开叶片区域，剔除掉不是叶片的杂色干扰区域；（2）确认叶片的边界以及叶脉。图像分割的结果对于后续的特征抽取算法至关重要，图像分割详细算法详见3.2节。

3.1.3 叶形特征计算

选取特征值方面前人已经有过很多成熟的研究，如祁亨年，寿韬，金水虎的《基于叶片特征的计算机辅助植物识别模型》[7]一文中定义的圆形度，王晓峰，黄德双，杜吉祥的《叶片图像特征提取与识别技术的研究》[8]中的面积凹凸比和周长凹凸比实际效果很好，本文中的残缺度和紧致度等指标借鉴了这几个特征的设计。

本课题采用的叶片叶形特征包含：

（1）凸包亏格Ei

叶片的凸包定义为包围叶片边缘的最小凸多边形，亏格是拓扑学中表示连通，可定向曲面代表沿闭简单曲线切开但不切断曲面的最大曲线条数。叶片凸包的亏格即为此特征值。针对叶片图像，亏格可以表示叶片被凸包包围后，凸包和叶片边缘组成的多边形有多少个孔洞。

（2）残缺度Sx

叶片凸包面积与实际面积的比值定义为叶片的残缺度。

（3）紧致度C

叶片叶边缘的周长的平方与叶片面积的比值定义为叶片的紧致度。

（4）长短轴比值Li

叶片的长轴及短轴表征了叶片的粗细程度，针对简单的椭圆形，长条形叶片和复杂的五角星形叶片，长短轴定义不同，具体的定义及算法见3.3.6节。长短轴比值即为长轴除以短轴所得的数值。

（5）角点数目K

叶边缘上的角点的个数为角点数目特征值。

以上五组特征值区分度较大，其详细算法见3.3节。

3.1.4 叶脉特征计算

本课题采用的叶脉特征包含：

（1）主脉条数Lx

在识别算法中，叶脉长度超过叶片长轴70%的被认为是主脉，侧脉通常不会超过这个阈值，细脉无法准确识别，因此会在图像分割时被去除掉。

（2）叶脉类型T

根据主脉的交汇情况可以判断叶片的叶脉类型，文章主要进行网状脉和平行脉的判别，其他细分类型暂时无法区分。

（3）最长最短主叶脉比值Lv

当主脉不止一条的时候，最长的主脉与最短的主脉的值定位为此特征值，主脉只有一条时，此特征值为1。

以上三种特征是可以由图像普遍得出的叶脉特征值，其详细算法见3.4节。

3.1.5 可信度判定

可信度判定，主要用来判断图像信息抽取得到的特征值当中易受到图像精细度影响的特征的可靠程度。易受图像精细度影响的特征包括角点数目K，主脉条数Lx和最长最短主叶脉比值Lu三个特征。

可信度根据图像精细度计算，实验中若图像精细度r不超过0.75，则认为无法抽取到叶脉特征和叶边缘的角点特征，从而避免因为图像的原因，部分特征值计算出错误的结果，造成抽取的向量中出现异常值。

3.2 区域分割算法设计

本次实验的区域分割算法分为四个步骤。

步骤1利用Canny算法抽取图像的边缘。

若将图像视为一个二维函数a=f(x，y)，a为x，y坐标上的色彩数值，则可以知道，在颜色变化的地方，该函数的导数将很大，而对于周围点，导数则很小，针对这一特性对图像进行拉普拉斯变换，既可以得到边界曲线。Canny对此算法做了改进[9]，增加了一个滤波过程，使得算法更加可靠。

图2为未经过任何处理的原始叶片图像。

图2 叶片原始图像

可以看到光线并不均匀，并且右侧有部分颗粒状的纹理干扰。

经过图片预处理和Canny算法后，可以得到其边界如图3。

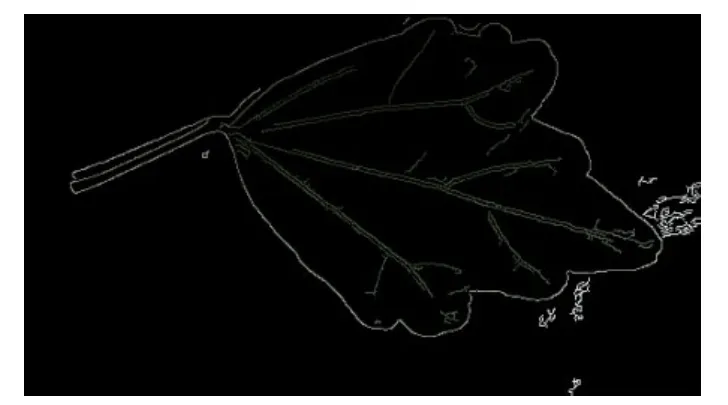
图3 经过Canny边缘检测处理后图像

得到的边界存储于本文设计的数据结构中，由于有杂色干扰，故本文的数据结构中也包含这些干扰点。

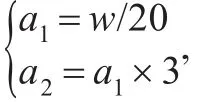
步骤2连通曲线抽取。

在此步骤中需要针对上一步骤所得到的边界点集，计算所有连通曲线Ai的集合，由于一张图片除了包含叶片边缘的连通曲线，还可能包含叶脉连通线，以及其他的各种杂色及干扰组成的小连通曲线，故i＞1。

对于图3的叶片，其边界点集合为C0（包括部分干扰点），则可以采用连通曲线扫描算法进行连通曲线的确定。

算法1连通曲线扫描算法

（1）针对C0中的每个点进行遍历，遍历顺序先沿X正方向，再沿Y正方向，对于C0中点A。

①若A左上方连续2×2区域中的点均未在C0内，则表明点A为一个新的连通曲线中的一个点，则连通曲线总数n加1，并创建记录连通曲线点集的数组Ai（其中i为持续递增的序号），并将点A加入该连通曲线数组Ai中。

②否则，表明A与其左上2×2区域中的点在同一个连通曲线Ax内，则将A及和A同在一个连通曲线中的所有点，均加入到那个已记录的连通曲线数组Ax中。

③如果A未加入Ax前已经有所在的连通曲线，则销毁那个曲线数组的记录，并将连通曲线总数n减1。

（2）继续扫描，直到扫描完C0中所有点。

（3）至此，将得到n个包含边界点的连通曲线的数组Ai，其中 0＜i≤n。

进行完上一步骤后，可以得到若干个包含着连接曲线的点的数组集合：{A0，A1，…，An}， 这些连通曲线有的尺寸很小，属于杂色干扰，也可能是不清晰的叶脉细脉图像，这些图像随机性较大，会干扰后续计算，因此需要针对集合中每一个数组Ai进行过滤干扰曲线的算法。

算法2过滤干扰曲线算法

（1）计算整个图片像素点的数目：s=w×h，其中w和h分别为图片的长和宽，记阈值T=s×0.000 2，M=s×0.000 5（可以针对参数进行调整，公式中参数为实验中采用值）。

（2）若Ai中元素个数不超过阈值T，则认为该连通曲线为杂色斑点的边缘曲线或与主脉断开的侧脉及细脉曲线，删除Ai。

（3）针对没有被筛除的连通曲线，记曲线中所有点的x坐标的最大值Xmax，最小值Xmin，y值的最大值Ymax，最小值Ymin，计算L=max{(Xmax-Xmin)，(Ymax-Ymin)}，S0=L2，若S0小于阈值M，则认为该连通曲线为若干杂色点组成的色块，则删除Ai。

上述算法本质是删除点数过少或面积过小的连通曲线，减少后续运算的运算量。

由最后实验结果验证，完成此步骤后，基本大部分的干扰曲线均被去除。剩余的部分为叶脉和叶片，以及一些较大的背景形状，多数情况下背景形状与叶片的轮廓并不连通，个别情况下连接可以通过后续算法区分。

步骤3连通域抽取。

上一步骤所获取到的连通曲线集合，包含了不闭合的叶脉和大块的杂色块边缘以及叶片的轮廓，这一步骤中将利用连通域抽取算法抽取出闭合的叶边缘曲线所构成的连通域。

算法3连通域抽取算法

（1）对于剩余的每段连通曲线Ai，记Ai中元素个数为N，记阈值T=N/10，取算法2中得到的L，记阈值N=L/50，建立一个栈S，一个分支点集合数组Ps（后续计算会使用）。

（2）取Ai中的第一个点P0(X0，Y0)开始，对P0执行步骤（3）。

（3）对Ai中的某个点Px，将Px进栈，寻找以其为中心周围4×4区域内的相邻点。

①若存在多个邻接点，则先取Y最小的，若Y相同，则先取X最小的，并将Px存入Ps中，记取到的点为Px+1，若仅存在一个相邻点，则取此点为Px+1，对于Px+1，若Px+1不在栈内，则对Px+1执行步骤（3）。否则，创建一个存储连通域点集的数组Bj，复制从栈顶到Px+1元素的所有元素进入Bj，若Bj中元素个数大于T，则保留Bj，并将该连通曲线Ai内包含的连通域变量n加1，否则销毁Bj。

重复此步骤直到所有Px的相邻点均已处理，Px从栈顶退栈，继续计算。

②若Px不存在邻接点，若栈内元素数目超过阈值T，且Px距离栈底元素的距离小于阈值N，则创建一个存储连通域点集的数组Bj，复制栈顶到栈底的所有元素进Bj，并将该曲线内包含的连通域变量n加1。

Px从栈顶退栈，继续计算。

（4）若栈内元素总数超过阈值T，则计算栈顶和栈底元素的距离，若距离小于阈值N，则创建一个存储连通域点集的数组Bj，复制栈顶到栈底的所有元素进Bj，并将该曲线内包含的连通域变量n加1。

（5）进行上述步骤直到栈空。此时由算法可知，所有的连通域曲线均记录在Bi数组中，取所有数组中包含最多点数的数组作为叶片的外边缘连通域E，算法结束。

经过以上步骤算法后的图像如图4。

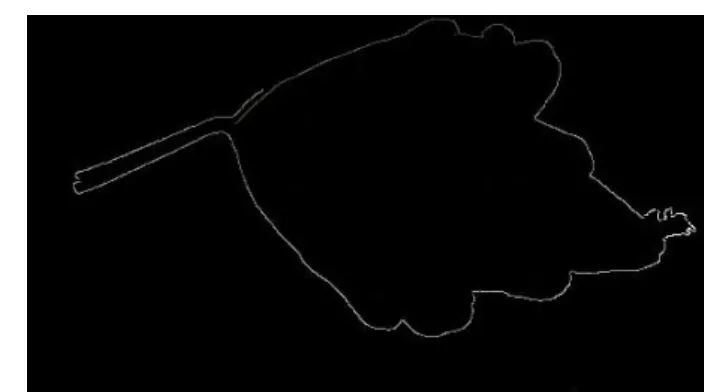
图4 连通域抽取算算法得到的叶片外边缘

步骤4去除图片上的叶柄和杂色块干扰。

在算法3中找到的连通域E，依然存在以下问题而无法用于直接计算：

由于受到叶柄的摆放方向以及叶柄阴影等因素的影响，叶片形状在叶柄部分随机性较大。叶柄部分对识别并无贡献，还会造成叶形判断上的干扰。

一些背景上的干扰会和叶片连在一起（少数情况），造成叶片的小尖角等不良干扰。

因此需要对所得的连通域点集E进行去除杂色块和叶柄的干扰的算法。

去除叶柄和粘连在叶边缘上的杂色块，采用算法思想为让曲线上每个点向该点的法线方向收缩，则最终叶片和叶柄以及杂色干扰会分解成不相连的部分，但由于法向量计算时计算量较大，故采用了近似的向量相加的算法，也可以达到向内收缩的效果，且效率较高。

算法4连通域变形算法

（1）建立记录点的数组Bs。

（2）针对E当中的每一个元素P(x，y)。

（3）若P不在算法3中记录的Ps集合内，取其相邻的左右两个点P1，P2，记向量PP1，PP2，分别取和PP1，PP2相 等 长 度 且 分 别 垂 直 于PP1，PP2的 向 量p0，p1， 记Px=P0+P1，设px的坐标为 (x0，y0)， 则点P向内收缩得到的新点为p0(x+x0，y+y0)， 将p0存入数组Bs，并记录p0所对应的原始点P。

（4）否则，继续其他点的计算。

（5）对Bs数组中的点重复步骤（2），重复次数为T（实验中T为10），对得到的点集再次算法3，将得到新的边缘数组，这次的边缘数组将不包含叶柄和杂色块。如图5。

图5 进行连通域变形后得到的叶边缘

可以看出缩小后的杂色块和叶柄均消失了，且边缘变粗，因为点更密集了，针对变形得到的结果，结合算法3中得到的连通域E，可以利用以下算法得到无杂色块和叶柄干扰的叶边缘图像。

算法5连通域去干扰算法

（1）找出Bs中每个点在E中对应的原点P0，将P0加入到数组B0中。

（2）检查分支点集合Ps中每个点Px的邻接点是否在B0中，若在将Px加入B0中。

（3）由于杂色块被消除，叶片边缘连接杂色快的部分会有一段缺口，这段缺口可以用直线进行修补。对所有被加入到B0中的Ps中的点Px：

①建立一个数组A，将Px在B0中的邻接点加入数组A。

②将Px加入数组A，寻找Px在E中而不在A中的邻接点Px+1，若Px+1在B0中，执行③，否则对Px+1进行②。

③将A中第一个元素和最后一个元素取出，记为a1，a2，将线段a1a2之间的所有点加入B0。

（4）所得到的B0即为后续计算所要使用的叶边缘点集。

经过上述过程后，原图像图2所得到的最终叶片边缘图如图6。

图6 最终得到的叶边缘图

此时，叶边缘的信息记录在B0中，利用叶边缘包含叶脉这样的关系，可以对之前得到连通曲线进行过滤，去除掉不包含在B0中曲线（边界也不包含在B0内），剩下的连通曲线集合即认为是叶脉曲线集合V。

3.3 叶片叶形特征值提取算法

叶片特征值计算需要考虑叶片旋转和缩放的问题，再由于叶片形状存在细节上的变动，抽取有一定区分度的特征向量有一定难度。

在叶片的识别实验中，多采用拓扑不变量或者可以抵消掉大小和角度因素的比值作为特征量。

本次课题中采用的叶片叶形特征包含凸包亏格Ei，凸包面积与实际面积的比值Sx，紧致度C，长短轴比值Li，角点数目K等5组特征值，这五组特征值当中，亏格和角点数目为拓扑不变量，其余三组为比值，由等比例缩放的原则可以知道，这三组数也不受角度和大小的影响。

计算以上五组特征值需要计算一些其他的变量，具体算法描述如下。

3.3.1 质心 M0(xm0，ym0)的计算

计算该连通域B0内所有点x，y坐标的算数平均值，即为质心的坐标。

3.3.2 叶边缘长度L的计算

叶边缘的长度等于叶片边缘数组中点的数目，即B0中点的数目。

3.3.3 叶片面积s的计算

利用机器视觉的理论，可以得到叶片图像和叶片实际面积存在特定的比例关系[10]，而此处的叶片的面积可定义为连通域B0包含的点的数目。

算法6叶片面积算法

（1）记叶边缘数组B0中x，y的最小，最大值分别为xa，ya，xb，yb，记面积S， 初始值为0。

（2）对线段YaYb上每一点Y0，记扫描线为直线Y=Y0，沿扫描线向右扫描，记录扫描线上的点和B0中的点重合的次数，当重合次数为奇数次时，每扫描一个点，S加1。

（3）直到扫描完区域内的点，所得的S即为叶片的面积。

此种扫描算法较标准的向量叉积求和算法效率高一些。此算法利用了拓扑学的定理：区域内部点引一条射线，交区域边界奇数次，而区域外引一条射线，交区域边界偶数次。

算法如图7所示。

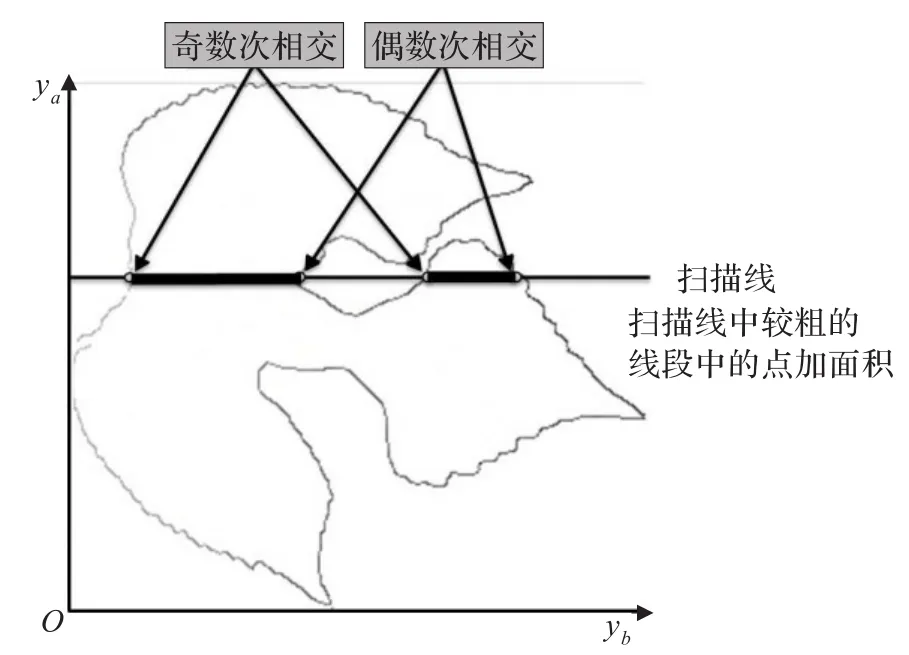
图7 面积算法图示

3.3.4 叶片凸包面积ss的计算

叶片凸包为包含叶片全部像素的一个最小凸多边形，图8展示了一个复杂叶片的凸包示意图，黑色实线为凸包。

图8 叶片凸包示意图

针对点集合计算凸包的算法已经有很成熟的Graham扫描法[11]，此处不再多描述。由于凸包是标准的凸多边形，且边数不多，可以采用标准的叉积相加的求面积算法，此种情形下算法效率较高。

算法7凸包面积算法

（1）首先利用Graham扫描法[11]针对连通域计算凸包边界点数组bt，扫描时按顺时针进行，故bt数组中元素也按顺时针顺序排列。

（2）记坐标原点为O，记所求面积为S，对bt中的每个点Pi，若不是数组的最后一个点，则记Pi的下一个点为Pi+1，记向量Xi=OPi，向量Xi+1=OPi+1。

①计算x=Xi×Xi+1，令S的值等于S+X（×表示向量做叉积）。

②重复此过程直到每个点计算过。

（3）S即为所求的凸包面积。

凸包的计算是稳定的，因为包围平面上任意多点的最小多边形总是存在，无论锯齿边，或者圆滑的边，都可以用若干折线进行拟合，拟合的曲线即可计算面积。即使存在锯齿边的叶片，由于锯齿部分虽然很不规则，但所占面积极小，也不会对凸包面积造成巨大的决定性影响，只会使得凸包面积在小范围内波动而已。

3.3.5 凸包亏格Ei的计算

凸包亏格为凸包与叶片边界组成的图形中孔洞的数目，图8的凸包亏格为5。凸包亏格算法结果将影响后续的长短轴计算。凸包亏格的计算应排除因为毛边叶片造成的影响。

算法8凸包亏格算法

（1）记录算法7中所得的凸包边界点数组bt，建立存储亏格存在的凸包边界数组Ed，记阈值R=w/70，w为图片的长度，及凸包亏格为Ei，初始值为0。

（2）针对叶片边缘数组B0中的每个点P(x，y)，连接质心M0和点P，延长此线段直到与凸包边界相交，设相交的边界为EiEi+1，记交点为P1(x0，y0)， 若

①P1与P的距离小于阈值R，则继续扫描。

②否则，查看数组Ed中是否存在此边界EiEi+1，若存在则继续扫描，否则凸包亏格Ei加一，并且将凸包的此段边界加入Ed。

（3）直到所有边界点均扫描完毕，Ei即为所求的凸包亏格。

凸包亏格对于特定形状为拓扑不变量，但是对于同一类叶片，其形状可能存在微妙的差异，使得凸包亏格会在一定范围内波动，但由于叶片的相似性，一般叶片的波动范围不会超过±1。

对于锯齿边造成的对亏格计算的影响，可以通过设置阈值R（参见算法描述）进行消除，若发现同类叶片的亏格差距过大，可以增大阈值R进行再次计算。

3.3.6 长短轴长度Lmax，Lmin的计算

对于凸包亏格为0的叶片，认为叶片形状为标准的凸多边形，其长轴定义为距离质心M0最远的叶边缘上的点与质心组成的线段，该线段的长度为长轴长度Lmax。短轴定义为距离质心M0最近的叶边缘上的点与质心组成的线段，该线段的长度为短轴长Lmin。此情况下的长短轴示意图如图9，图中蓝色线段代表叶片的短轴，红色线段代表叶片的长轴。

图9 凸包亏格为0时的长短轴示意图

对于凸包亏格大于0的叶片，由于其叶形状较复杂，故定义长轴为距离质心M0距离为周围其他点的极大值的点与质心组成的线段，相应的短轴为距离质心M0距离为周围点的极小值的点与质心组成的线段，针对此种情况，长轴和短轴可能有多个。如图10示意了凸包亏格为5的叶片的长短轴情况，此叶片蓝色线段代表短轴，红色线段代表长轴。

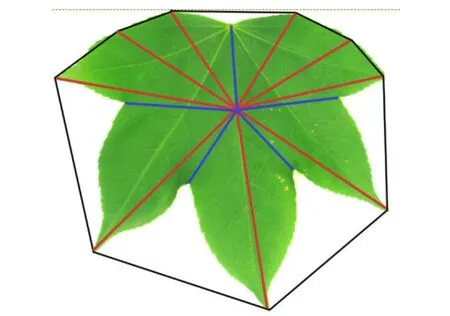
图10 凸包亏格不为0时的长短轴示意图

由凸包性质可以知道，凸包的每个顶点都是距离质心距离的极大值点，且产生亏格的凸包线段内，必有距离质心距离的极小值点。

算法9凸包亏格不为0的叶片的长短轴算法

（1）建立记录长轴长度的数组L1，建立一个与算法8中Ed中包含边数相等的数组L0，L0中的每个元素对应Ed的一个边界。

（2）对每个边界点P(x，y)

①若此点为凸包顶点，计算该点到质心的距离，记录到长轴数组L1当中。

②否则，若此点与质心连线延长后经过凸包边界EiEi+1，若算法8中的Ed包含EiEi+1，则记算此点距离质心的距离Lx，若Lx小于L0中记录的对应EiEi+1的值，则将L0中的该值替换为Lx。

③其他情况继续扫描。

（3）针对所有的L1记录下来的长度，计算其均值为长轴长度Lmax，针对所有L0记录下的长度，计算短其均值为短轴长度Lmin。

长短轴计算的稳定性类似凸包亏格的稳定性，易受到锯齿边的影响，但在凸包亏格计算中，通过设定合理阈值，可以规避这种形象。由于此步骤采用了上一步的边界计算结果Ed，故算法稳定。

3.3.7 叶片边缘曲线角点数目K的计算

对叶边缘图形利用Harris角点检测的改进算法。算法由Krystian.Mikolajczyk，Cordelia.Schmid两人提出，在基本的Harris角点检测算法基础上，加入了数学处理，使得检测可以在经过仿射变换的图像也得到较为准确的值[12]。针对叶片这种特殊的边缘类型，文章参数选取参考了王玉珠，杨丹，张小红的《基于B样条的改进Harris角点检测算法》[13]一文。课题的算法由OpenCV实现，可以获得叶片边界上角度剧烈变化的点，记录在一个数组内。角点计算的效果图如图11，红色圈为计算得到的角点。

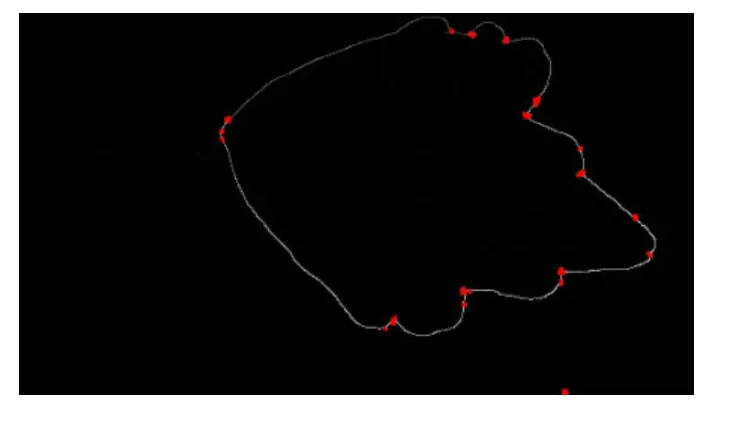
图11 叶边缘角点计算结果

OpenCV中的Harris检测需要设置两个参数：

BlockSize：设置算法检测角点的图像块大小，实验中默认使用的2。

KSize：用于进行图像过滤的参数，影响点的数目，实验中设置为3。

角点数目K可以由算法的结果经过算法过滤得到。

角点数目在计算中存在不稳定的情况，但在去除掉相邻过紧的点之后，会发现特定叶片的角点数目总是处在一个比较稳定的范围当中，这是因为叶片的形状大体相似。

3.4 叶脉特征值抽取算法

为了进一步提高叶片的区分度，本次实验还尝试提取了叶脉所包含的特征，目前可以计算的叶脉特征值包括：主叶脉条数，叶脉类型以及最长主叶脉与最短主叶脉的比值。主脉的定义参考《一种改进的叶脉建模方法》[14]中的描述。

叶脉类型大体分为三类：分叉叶脉，网状脉，平行脉。叶脉中最显著可辨别的是叶脉的主脉，本次实验中主要通过区分叶片中包含的较长的连接曲线与长短轴的比值来判断曲线是否主脉，再根据主脉的条数，交汇点等信息来判断叶脉的类型。

图2所示叶片去掉叶片叶边缘的叶脉图像如图12。

图12 抽取的叶脉图像

抽取主叶脉长度和叶脉类型特征的具体算法需要三个步骤，描述如下：

步骤1利用Hough变换，找出叶脉图片中的所有长直线。

Hough变换是利用极坐标下直线的表示特性，通过对图像中的点进行扫描，计算极坐标下两点或多点间是否构成直线，从而找出图中直线的算法[15]。

Opencv的Hough变换有以下几个参数需要设置：

Rho：距离解析度，采用默认的1 px。

Theta：角度解析度，为了检查到所有可能的直线，实验中采用了ƛ/(180×60)的解析度。

Threadhold：阈值，只有当直线的投票超过该阈值时，才会进入结果集，实验中采用了2作为阈值，为了找到所有可能的直线。

minLineLength：最短长度，只有当直线的长度超过该值才可进入结果集，实验中采用了叶片长轴长度Lmax的70%。

maxLineGap：最大间断距离，直线如果中间间断距离小于此值，会被认为是同一直线，实验中采用了图像长度的1/40。

变换后的叶脉图像如图13，红色线条为利用Hough变换找出的长直线结果。

图13 Hough变换后获得的图像结果

可以看出主要的叶脉均被查找出来。Hough变换所得的结果记录在数组Hi当中。

步骤2合并斜率相近，有距离较近端点的线段。

算法10叶脉长直线合并算法

（1）建立存储合并后叶脉线段的数组V。

（2）对Hi中的每条线段Li，对比该直线斜率与其他Hi中所有直线Lx的斜率，若两者之差的绝对值不超过过阈值K（K实验中取0.05），则查找两条直线的四个端点，若直线的Li的某个端点与Lx的某个端点之间的距离小于阈值D（D取图像长度w的0.005），则认为Li和Lx是同一叶脉，合并两条直线为L，记录L到V。若无直线可与Li合并，则记录Li进数组V。

（3）继续查找，直到每两条直线都被比较过。

（4）可知V中记录的是叶脉的线段集合。

步骤3计算叶脉类型和叶脉长度。

利用算法10中的结果，可以知道结果中的每条直线，都是叶片的主脉，故主脉条数可以由V中直线的条数表示。计算V中所有直线的长度，记最长的为Vmax，最短的为Vmin。

利用算法10中的结果，计算V中每两条直线的交点，若所有交点相互间距离不超过阈值D（D取图片长度的0.005），则证明所有叶脉均交于一点，证明叶脉形状是网状脉，否则认为是平行脉。

由算法可以看出，在抽取出叶脉的主脉中所有可能的长直线时，算法利用长度限制过滤了所有过短的侧脉及细脉，由于参数可调整，若结果不理想，则可以通过适当调整叶脉长度的阈值来使得结果更加合理。计算出来的叶脉也会按照斜率和是否相接来进一步合并，从而使得所得的直线尽可能拟合叶脉的真实情况。从结果来看，特定叶片的叶脉特征基本符合常理，也稳定在一定范围内。

3.5 特征值计算

最终利用上述结果，便可以计算出表征叶片的8个特征值：

由于这个叶片形状特征是一个归一化的二阶矩不变特征（参考文献[4]中的结论），因此在图像旋转，缩放等变化的情况下，具有特征的鲁棒性。

同紧致度，此特征值为叶片形状特征中的归一化一节矩不变特征。Lmax和Lmin的计算稳定性请参考3.3.6节。

此特征值为归一化二阶矩不变量，其中凸包面积ss的稳定性可参见3.3.4节的说明。

（4）凸包亏格Ei在3.3.5节中求出。

此特征为拓扑不变量，不受缩放和旋转的影响，其稳定性请参见3.3.5节。

（5）角点数K在3.3.7节中求出。

此特征为拓扑不变量，稳定性参见3.3.7节描述。

（6）主脉条数Lx在3.4.3节中求出。

此特征为拓扑不变量，稳定性参见3.4.4节描述。

（7）叶脉类型T在3.4.3节中求出。

此特征为拓扑不变量，稳定性参见3.4.4节描述。

此特征为归一化一阶矩不变量，不受旋转和缩放的影响。稳定性参见3.4.4节描述。

经过实验证明，这八组特征值很适合区分叶片的形状，其中凸包亏格e和面积比凸包面积S，这两组特征对于区分简单形状叶片（长条形，椭圆形）和复杂形状叶片（五角星形等）帮助很大，角点数对于区分毛边叶片和平滑边叶片的帮助很大，长短轴比和紧致度则区分了长条形叶片和比较圆的叶片，也可以区分复杂形状叶片的细长程度。主叶脉条数及主叶脉最长最短比也在比较某些形状类似的叶片发挥了作用。

4 系统实验结果

4.1 实验数据集介绍

实验的测试数据来源于在自然光照条件下，使用普通素描纸垫衬而拍摄的213枚10个种类的叶片。其中每个种类有18～22枚叶片，叶片的种类包括爬山虎，银杏，柳叶，梧桐叶等多种类型。图14～17为若干叶片样本图片样例。

图14 图片样例1

图15 图片样例2

图16 图片样例3

图17 图片样例4

4.2 实验方案介绍

利用第3章中描述的算法，获取到叶片的八个特征值信息后，利用LibSVM开源软件项目的支持，以SVM（Support Vector Machine，支持向量机）分类算法，进行了分类测试。

SVM为二分类算法，本次实验使用时，采用了将一个叶片和其他所有叶片区分开的策略，故针对每种叶片都进行了训练和测试。

其中由于银杏叶无法抽取叶脉，故银杏叶与其他树叶区分的实验中没有采用叶脉数据进行训练，而其他树叶的训练中，银杏叶的叶脉数据和被测试树叶相同，即无法通过叶脉特征将被测试树叶和银杏叶区分开。

测试时，先用一半的数据进行训练，取得分类平面后测试另一半数据是否分类准确。

若测试结果中某些特征值明显不符合常理，则可以查看算法中特定参数是否合适，并进行适当的调整，调整后再次进行实验。

若测试结果符合预期，则将训练数据集和测试集互换，再次测试分类是否准确，以防止出现参数的过拟合现象，确保分类器的可推广性良好。

4.3 实验结果介绍

测试表明，利用这8个特征向量对叶片种类进行识别，识别的正确率高达91.5%，且分类器具有良好的可推广特性，在调换了测试数据集和训练数据集之后，仍能达到相当的识别正确率。

抽取叶片的特征值数据结果如表1。

实验中测试215个叶片的数据抽取，仅耗时61 s，平均每个叶片的数据计算在300 ms内即可处理完成。

5 结束语

本实验针对实际光照条件下，在实际的垫衬背景下拍摄的图像进行图像分割和特征值抽取，通过多种算法的综合使用，使得叶片图像可以较精确地转换为可靠的，显著的特征值，且经过实际编码实验，算法可以正常运行，计算出的结果也有意义，区分度比较大。

在一个小的数据集上测试，利用SVM分类算法可以达到91.5%的准确率，且执行效率较高，平均每个叶片的抽取分析耗时也不超过300 ms，算法具有实际应用的可能。

目前这套算法中还存在以下不足，考虑未来改进：

（1）图像分割过程中，采用的canny算法的滤波参数在各种明暗不同图片中均采取了统一值，使得有些图像的分割细节缺失很大，有些图片的分割出了很多的杂色色块，考虑后期研究如何从图片中得到滤波参数，从而使得边缘检测出的结果更加优化。

（2）叶片的叶边缘抽取过程中，仅考虑了叶片为单连通域的情况，结果发现一些叶片上会有孔洞，而这类叶片的孔洞会被当作叶脉处理，虽然现阶段无法处理曲线叶脉故不会对算法造成不良影响，但对于叶片识别来说，重要的信息没有被抽取到，考虑后期改进边缘抽取算法，以使得可以抽取到叶片当中的孔洞信息。

（3）叶脉检测算法目前只能支持直线的叶脉，对于某些曲线型叶脉（例如弧形平行脉）则无法进行计算，实验原计划利用曲线的hough变换算法来抽取曲线叶脉，但效果不理想，后期会考虑优化参数或者自行设计曲线叶脉的抽取算法，以使得叶脉的抽取覆盖更加广泛的叶片类型。

此外在算法效率上区域分割算法中的联通曲线和连通域抽取是效率的瓶颈，考虑后期进行算法的优化，从而使系统执行效率更高。

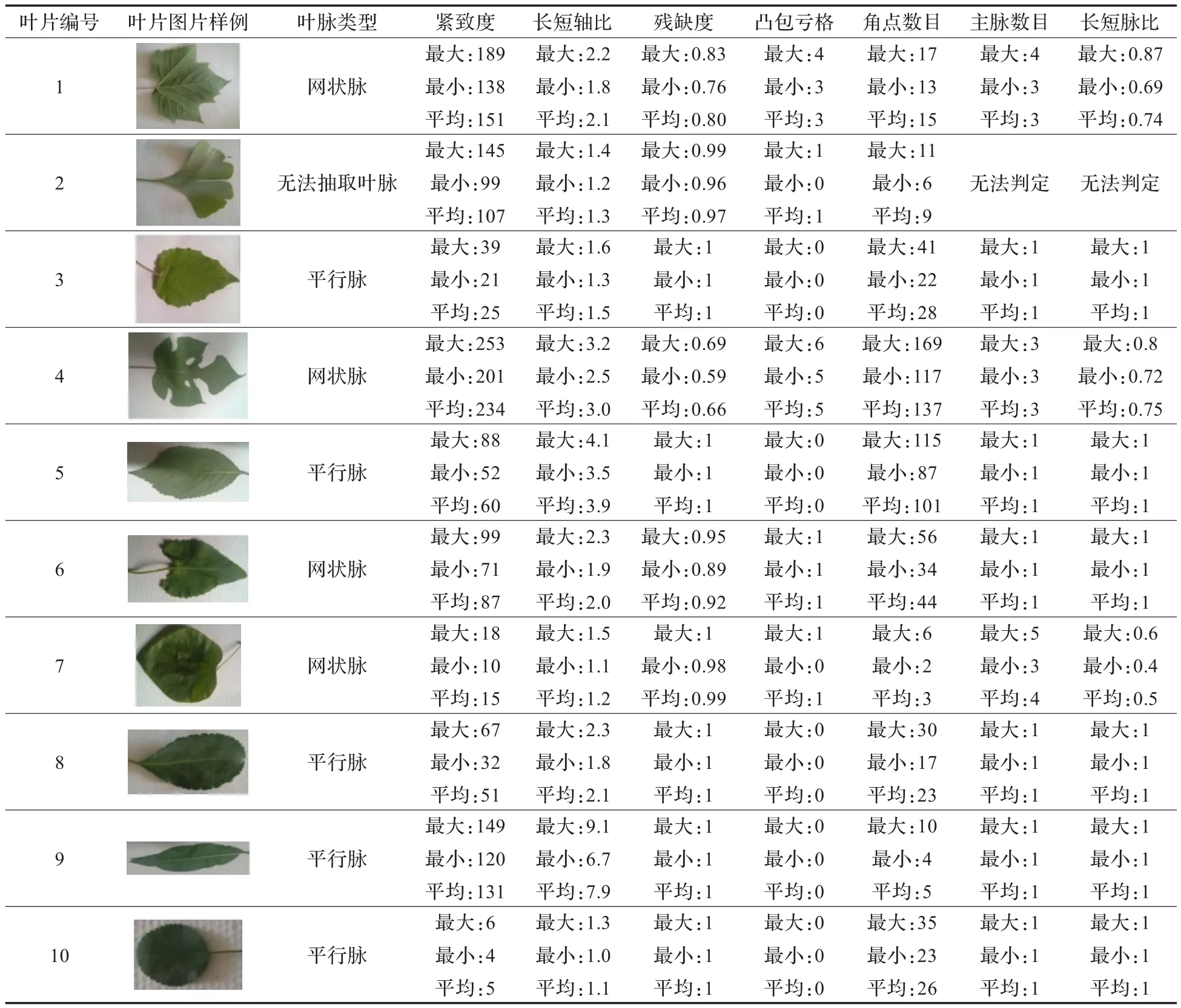
表1 实验结果汇总表

[1]Ingrouille M J，Laird S M.A quantitative approach to oak variability in some north London woodlands[J].London Naturalist，1986，65：34-46.

[2]Guyer D E，Miles G E，Schreiber M M，et al.Machine vision and image processing for plant identification[J].Transactions of ASAE，1986，29（6）：1500-1507.

[3]傅星，卢汉清.应用计算机进行植物自动分类的初步研究[J].生态学杂志，1994，13（2）：69-71.

[4]ChakiJ，Parekh R.Plantleafrecognition using shape based features and neural network classifiers[J].International Journal of Advanced Computer Science and Applications，2011，10（2）：41-47.

[5]侯铜，姚立红，阐江明.基于叶片外形特征的植物识别研究[J].湖南农业科学，2009（4）：123-125.

[6]汤晓东，刘满华，赵辉，等.复杂背景下的大豆叶片识[J].电子测量与仪器学报，2010，24（4）：385-390.

[7]祁亨年，寿韬，金水虎.基于叶片特征的计算机辅助植物识别模型[J].浙江林学院学报，2003（3）：281-283.

[8]王晓峰，黄德双，杜吉祥.叶片图像特征提取与识别技术的研究[J].计算机工程与应用，2006，42（3）：190-193.

[9]Canny J.A computational approach to edge detection[J].Pattern Analysis and Machine Intelligence，1986，8（6）：679-698.

[10]陈鼎才，王定成，查金水.基于机器视觉的现实叶片面积测量方法的研究[J].计算机应用，2006，26（5）：1226-1228.

[11]Graham R L.An efficient algorithm for determining the convex hull of a finite planar set[J].Information Processing Letters，1972，1：132-133.

[12]Mikolajczyk K，Schmid C.Scale and affine invariant interest point detectors[J].International Journal of Computer Vision，2004，60（1）：63-86.

[13]王玉珠，杨丹，张小红.基于B样条的改进Harris角点检测算法[J].计算机应用研究，2007（2）：192-205.

[14]谷文哲，金文标，张智丰.一种改进的叶脉建模方法[J].计算机工程与应用，2010，46（21）：242-245.

[15]Duda R O，Hart P E.Use of the Hough transformation to detect lines and curves in pictures[J].Artificial Intelligence Center，1971.