卫星点波束的移动目标指向优化研究*

韩 湘,郭新哲,邬基博

(中国人民解放军61096部队, 北京 102300)



卫星点波束的移动目标指向优化研究*

韩 湘,郭新哲,邬基博

(中国人民解放军61096部队, 北京 102300)

由于星载点波束天线覆盖范围较小，且可转动次数受使用寿命限制，当用于大范围机动用户通信时，需对其指向进行优化设计，在满足通信需求的前提下，尽可能延长天线的使用寿命。综合考虑卫星可视范围、点波束转动限位、点波束调整裕量等实际因素，提出了一种迭代搜索的点波束指向优化设计算法，并进行了仿真分析。仿真表明，这种算法在满足通信要求的同时可有效减少点波束移动次数，并为点波束天线的高效使用提供了途径，具有很强的工程应用价值。

点波束天线； 移动目标； 迭代搜索

0 引 言

随着我国航天及通信事业的发展，点波束天线以其灵活性好、增益高、安全保密性强等特点，在各类通信卫星上获得了越来越广泛的应用[1-2]。由于点波束覆盖范围有限，对运动范围广、跨度大的移动用户来说，必须根据通信需要适时调整点波束天线指向，以确保点波束对通信目标的可靠覆盖。但是，点波束天线的转动寿命有限，点波束指向调整的次数直接影响着点波束天线的使用寿命。因此，为实现点波束天线的高效使用必须对点波束天线的指向进行优化设计，在满足通信质量要求的同时，尽可能减少点波束移动次数。

近年来人们对点波束天线的指向理论己经进行了一些研究。文献[3]在己知卫星位置、速度和目标位置的前提下，提出了目标可见性及天线方向角的计算方法。文献[4]提出了卫星对地面覆盖区的计算模型，并分析了地球自转及轨道摄动对于卫星地面覆盖带的影响。文献[5]提出了一种由天线波束覆盖区边界点采样计算覆盖区边界经纬度坐标的方法。文献[6]基于天线功率辐射模型，针对多个静止目标的情况提出了有效全向辐射功率最优时的点波束指向算法。但是这些研究大多仅针对点波束指向固定目标时的覆盖区域进行了理论分析。文献[7]通过计算点波束中心和覆盖范围，提出了一种针对移动目标的点波束指向优化算法，但该算法并未考虑点波束移动限位、星视地球范围、点波束调整裕量等实际因素。

本文基于STK(Satellite Tool Kit)软件，对点波束的移动目标指向优化问题进行研究。一方面，综合考虑星视地球范围、点波束限位角度等实际因素，通过迭代搜索的方法优化选取各点波束中心，使每个点波束对运动路线的覆盖达到最大；另一方面，在两点波束间设计一定的重叠区并设置转换点，当目标到达转换点时即进行点波束调整，使点波束指向调整有一定裕量，确保点波束通信稳定可靠。仿真表明，所提优化指向算法可在满足通信质量要求的同时有效减少点波束移动次数，具有很高的实际应用价值。

1 算法描述

基于贪心算法[8]的思想，在确保点波束对目标运动路线可靠覆盖的前提下使点波束移动次数最少，也就是使每个点波束覆盖的运动路线达到最大，算法中通过迭代搜索的方法选取各点波束中心。以某一点波束中心的决策过程为例，其基本思路为：首先综合考虑点波束直径、限位角度和目标运动路线三方面因素，确定点波束中心初始位置；然后基于初始位置，分别沿经度和纬度的正负方向以一定步长为间隔进行迭代搜索，选取覆盖路线最长的位置为优化结果；最后，根据点波束重叠区范围，确定点波束调整的转换点。算法的主要步骤如下：

第一步 选取处于星视范围内的运动路线；

第二步 运动路线采样；

第三步 参数初始化。设置当前点波束序号为1，将路线起点作为待决策起点；

第四步 确定点波束中心初始位置；

第五步 通过搜索迭代的方法优化决策点波束中心；

第六步 计算点波束的调整点；

第七步 更新路线起点，返回第四步直至到达路线终点；

第八步 输出指向优化结果。

2 实现方法

根据算法思路，下面具体阐述主要步骤的实现方法。

2.1 路线采样

为降低实现复杂度，算法中基于一定的距离间隔对运动路线进行采样，以采样后的路线作为后续优化设计的依据。路线采样中采样间隔的选取直接关系到算法的性能和复杂度。如果采样间隔设置过大，则点波束所覆盖的采样点数量就会较少，从而导致迭代搜索结果发散；如果采样间隔设置过小，则会显著增加算法复杂度。算法中主要基于卫星姿态所引起的点波束指向抖动来设置采样间隔，即路线采样间隔Δs的取值均应大于该点波束变化量，避免因天线抖动造成优化结果失效或因路线采样过密造成算法复杂度增加。其计算方法如下：

当点波束指向星下点时，其点波束中心经纬度的变化量α和变化距离Δd可以由式(1)～(3)计算:

α=Rs×φ/Re

(1)

Δd=2π×Re×α/360

(2)

Δs≥Δd

(3)

其中,Rs=42 164为卫星距地心的距离，Re=6 378为地球的理想半径,φ。

2.2 初始位置确定

点波束中心的初始位置是后续迭代的基础，如果初始位置选择较差，将导致迭代次数增多，甚至迭代结果发散。如图1所示，算法中初始位置可由以下几步确定。

第一步 计算重心。首先，沿采样路线搜索，选取距路线起点的距离最接近于点波束直径的采样点，作为点波束初始终点；然后，计算路线起点与初始终点之间各采样点的重心，作为点波束中心的初始位置。

第二步 限位判断和修正。验证该初始位置是否处于点波束限位范围之外。如超出限位范围，则根据限位要求对初始位置进行修正，即保持其纬度不变，经度选取为该纬度对应的限位边界点。

第三步 起点判断和修正。求得初始点波束对路线覆盖的起止时刻；判断初始点波束是否覆盖路线起点。如未覆盖，则根据路线起点与点波束覆盖起点的位置差，对初始位置进行修正。修正后返回上一步，重新进行限位判断；如己覆盖待决策起点，则以该初始位置作为迭代搜索的初始值。

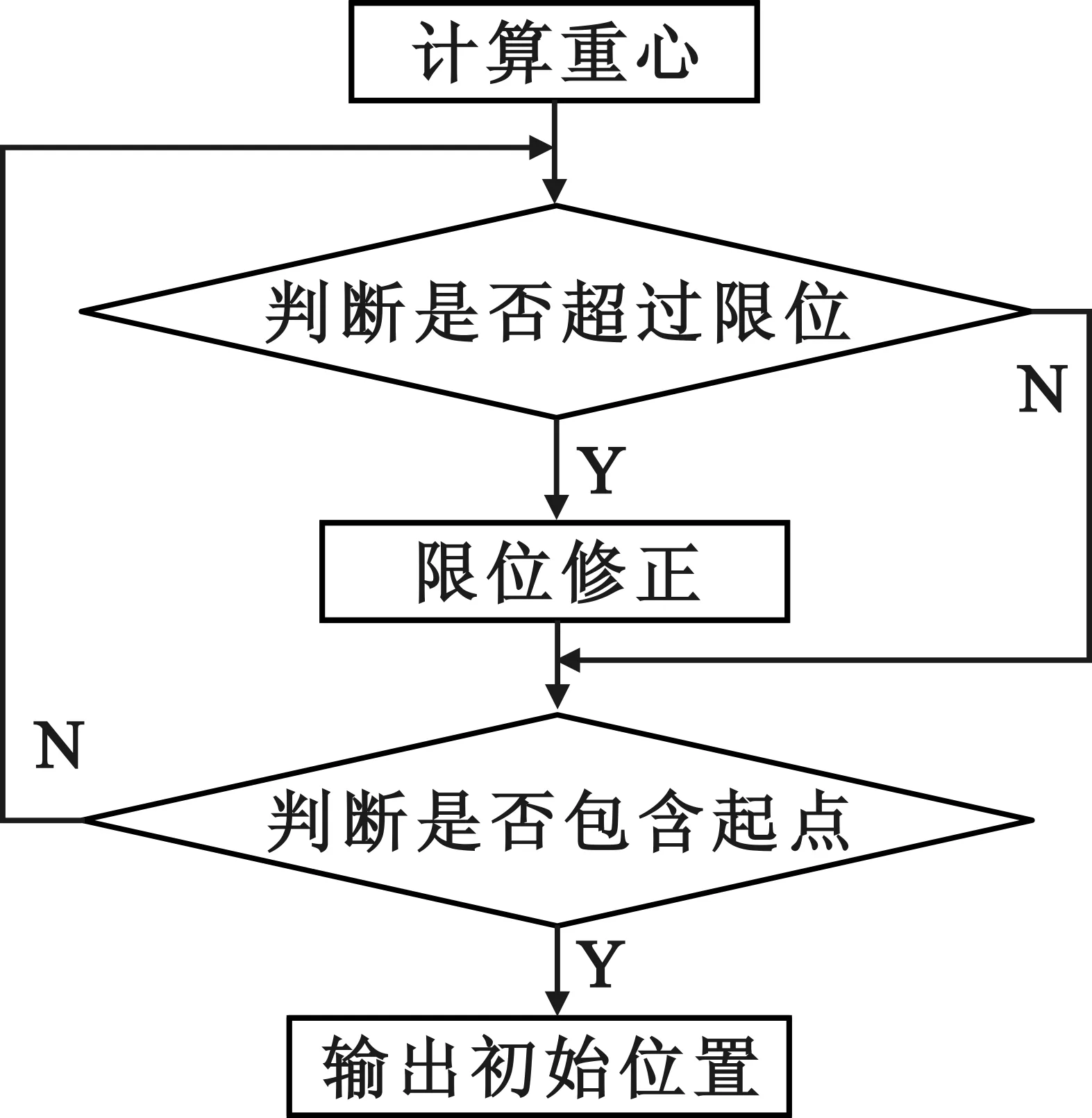
图1 点波束中心初始位置选择流程

2.3 迭代搜索方法

迭代开始时，首先定义初始点波束中心为参考点波束中心，并判断参考点波束是否己覆盖待路线终点。如可以覆盖，则说明己是最后一个点波束，无需优化；如未覆盖则进行后续优化。如图2所示，后续优化的实现方法如下：

第一步 基于参考点波束中心，分别从经度、纬度沿正负两个方向按一定步长Δθ进行步进搜索。步长的数值同样基于卫星姿态误差设置，需满足θ≥α。

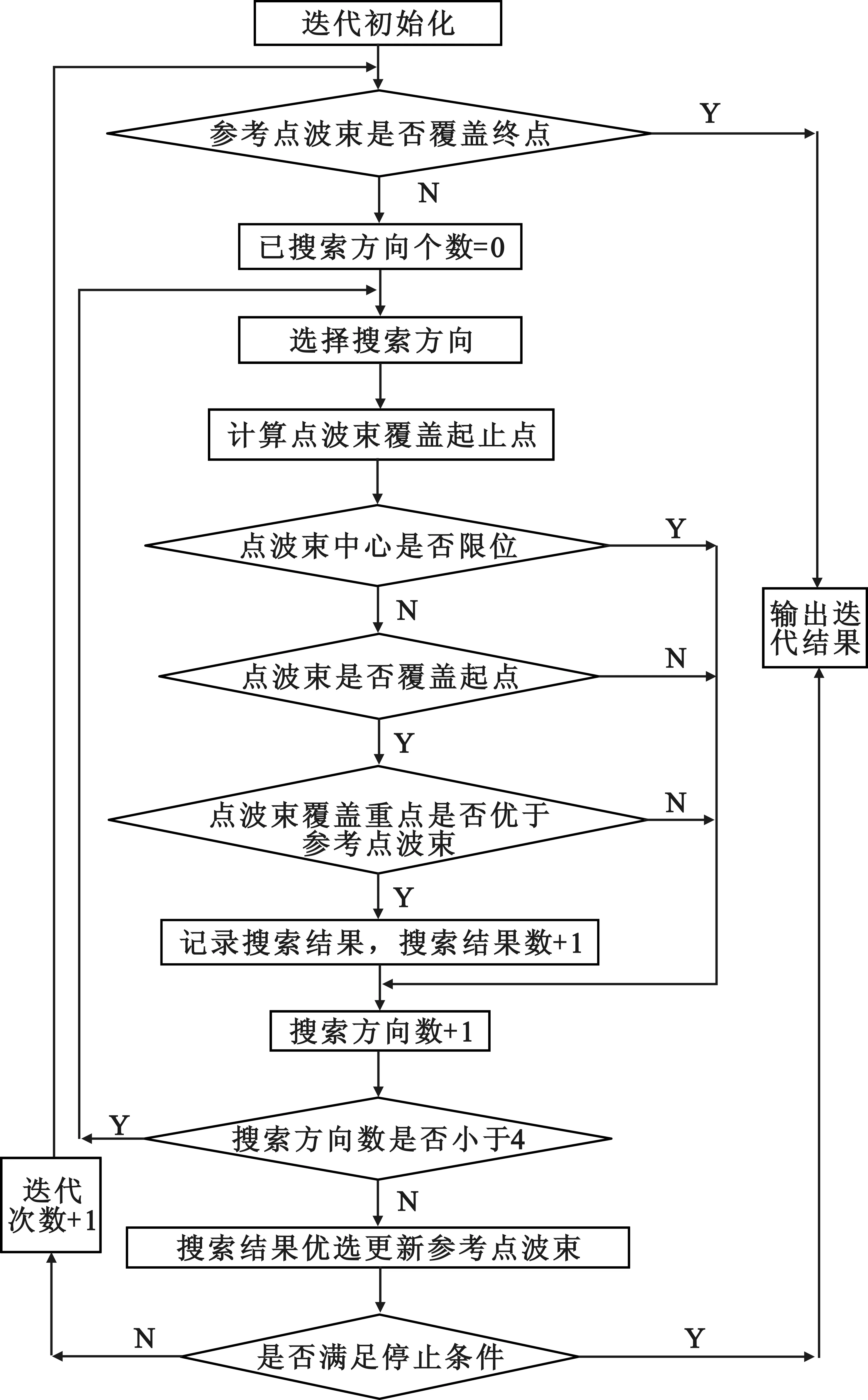
图2 迭代搜索算法流程

第二步 每次搜索中均计算所得点波束对路线的覆盖范围。如所得点波束出现：中心超出限位范围、未覆盖路线起点、路线覆盖范围小于参考点波束的覆盖范围，三者中任一种情况则抛弃所得点波束，否则记录所得点波束。

第三步 比较所记录的点波束覆盖范围，选取覆盖路线最长的点波束中心作为本次迭代的结果。

第四步 将所得迭代结果作为新的参考点，多次迭代搜索，直至到达路线终点或无法产生新的参考点。

2.4 计算调整点

如点波束序号大于1，则需计算调整点。基于已采样的路线，截取本点波束覆盖的起点与上一点波束覆盖的终点之间各采样点；求得各采样点的重心作为本点波束的调整点。

2.5 更新待决策路线

求得本点波束所覆盖路线的终点后，沿路线回退某一重叠距离作为后续决策的起点。

3 参数计算

算法中，星视范围和点波束限位的判断需计算目标位置偏离波束视轴的夹角。点波束限位的修正则需要计算限位边界的位置。下面分别给出目标位置与波束视轴夹角以及限位边界点的计算方法。

3.1 目标与波束视轴的夹角计算

在星视范围判断时，算法将卫星可视范围建模为一个以卫星为顶点的圆锥形波束，其波束角等于GEO卫星的对地视角，波束中心指向地心，该波束与地球的交线即为卫星的星视范围；同理，点波束限位范围建模时则将波束角设置为限位角度的两倍。基于这种模型，判断目标是否处于星视范围或点波束限位范围，可采用先计算目标位置与波束视轴的夹角β，再将其与卫星对地视角或点波束限位角度比较的方法实现。目标与波束视轴夹角β的计算方法如下。

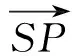
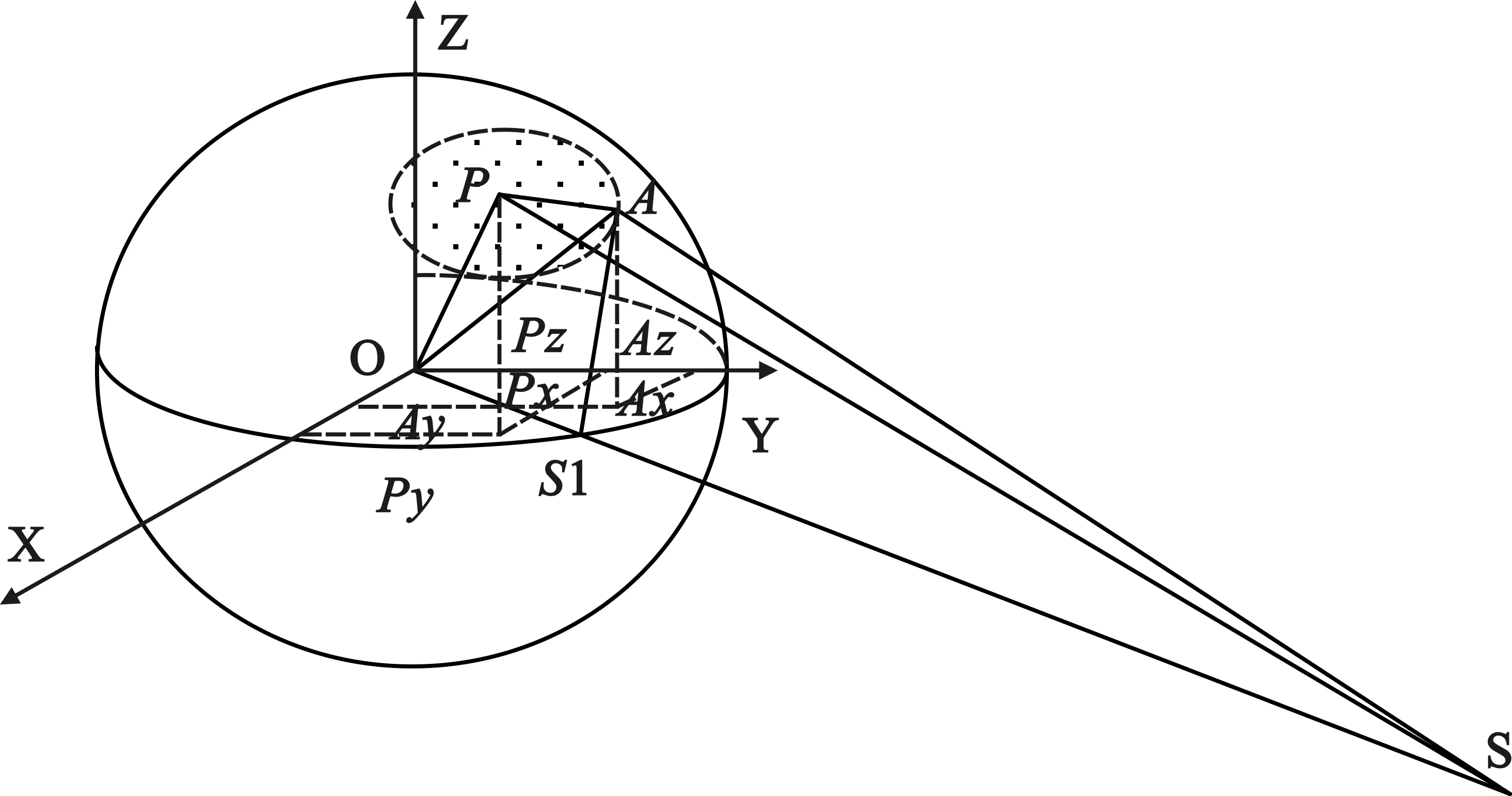
图3 目标与波束夹角示意图

首先，将各点表示为直角坐标的形式，分别记作A(Ax,Ay,Az)、P(Px,Py,Pz)和S(Sx,Sy,Sz)。以A点为例，其直角坐标可由式(4)-(6)计算：

Ax=Re·cosAlat·cosAlon

(4)

Ay=Re·cosAlat·sinAlon

(5)

Az=Re·sinAlat

(6)

然后，根据各点坐标计算两矢量夹角。

(7)

3.2 限位边界点计算

在实际应用中点波束中心的选取必须满足点波束天线的限位要求。算法中根据天线限位角度和卫星的定点位置，对超出限位范围的点波束中心位置，保持其纬度不变，以限位边界上该纬度对应点的经度作为修正后的经度，使其处于限位范围内。具体计算方法为：

设A点为点波束中心位置，其对应经纬度分别为Alat和Alon，对应的直角坐标为(Ax,Ay.Az)，点波束限位角度为θlimit，如图4所示。

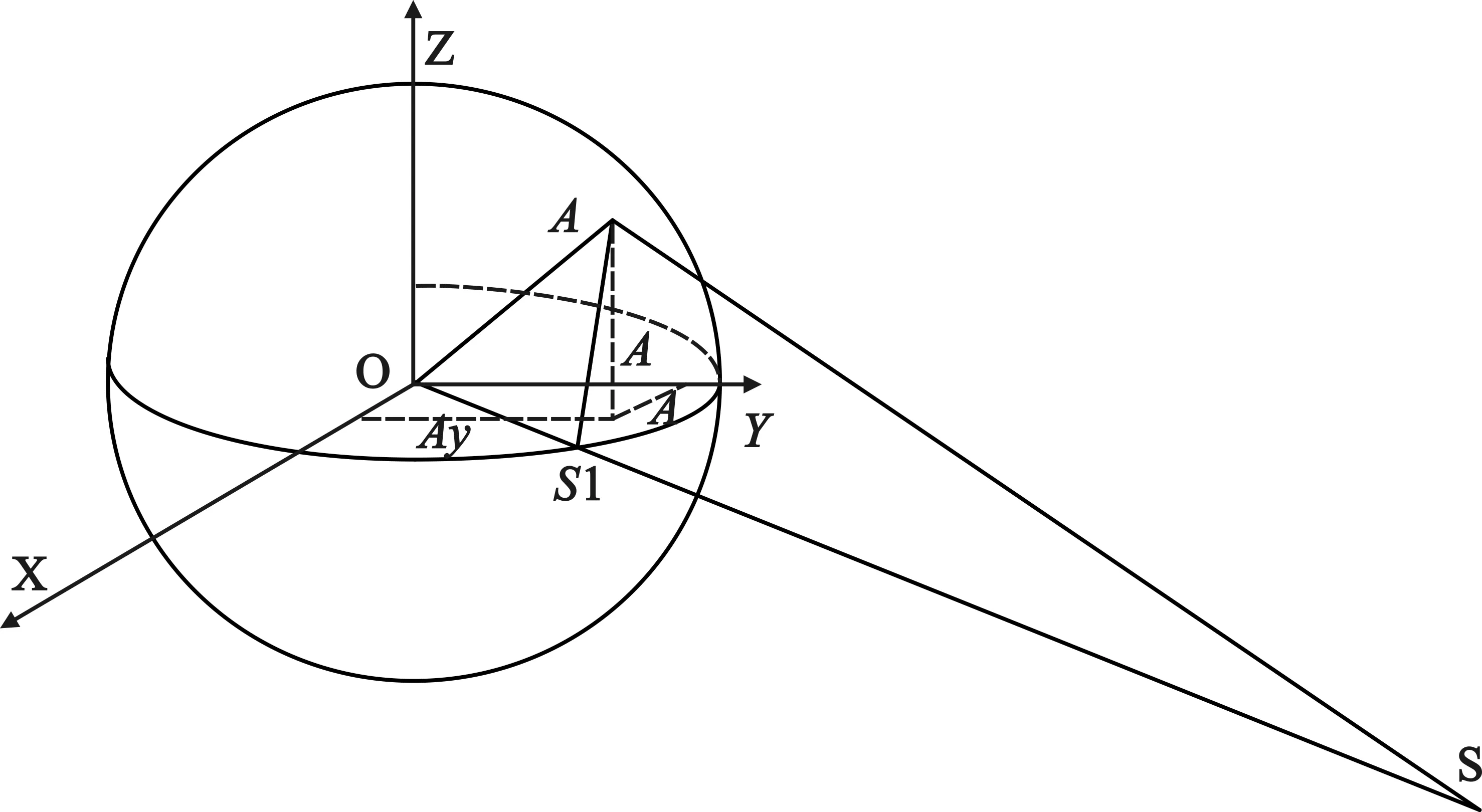
图4 目标与波束指向关系

在ΔOAS中，由式(8)计算∠OAS

(8)

进而由∠AOS=180-θlimit-∠OAS可以得到∠AOS。

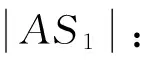
(9)

然后，联立式(10)求解：

(10)

可以得到Ax和Ay，如式(11)、(12)所示：

(11)

Ay=C1Ax+C2

(12)

其中

C1=-S1x/S1y

(13)

(14)

(15)

C4=-C1C2

(16)

(17)

(18)

根据所得到的Ax、Ay，由式(19)计算A点修正后经度Alon1：

(19)

4 仿真分析

4.1 仿真场景设置

假定某GEO卫星位于127°E，点波束半波束角为0.7°。某船只以18节的航速由(121.12°E、33.1°N)航行至(60.24°E、24°N)。航渡期间采用点波束通信，且为保证通信质量，两点波束间重叠范围不应小于100公里。仿真基于STK仿真软件实现，红色边界表示点波束限位范围。

4.2 仿真结果及分析

图5为未优化时点波束对移动目标的指向示意图。指向设计中采用半波束移动算法，即以航线与本波束边界的交点为下一个点波束的中心，以两点波束重叠区内航线的重心为调整点。这种方法的优点是算法简单，可靠性高；缺点是通信裕量过大，点波束移动频繁。

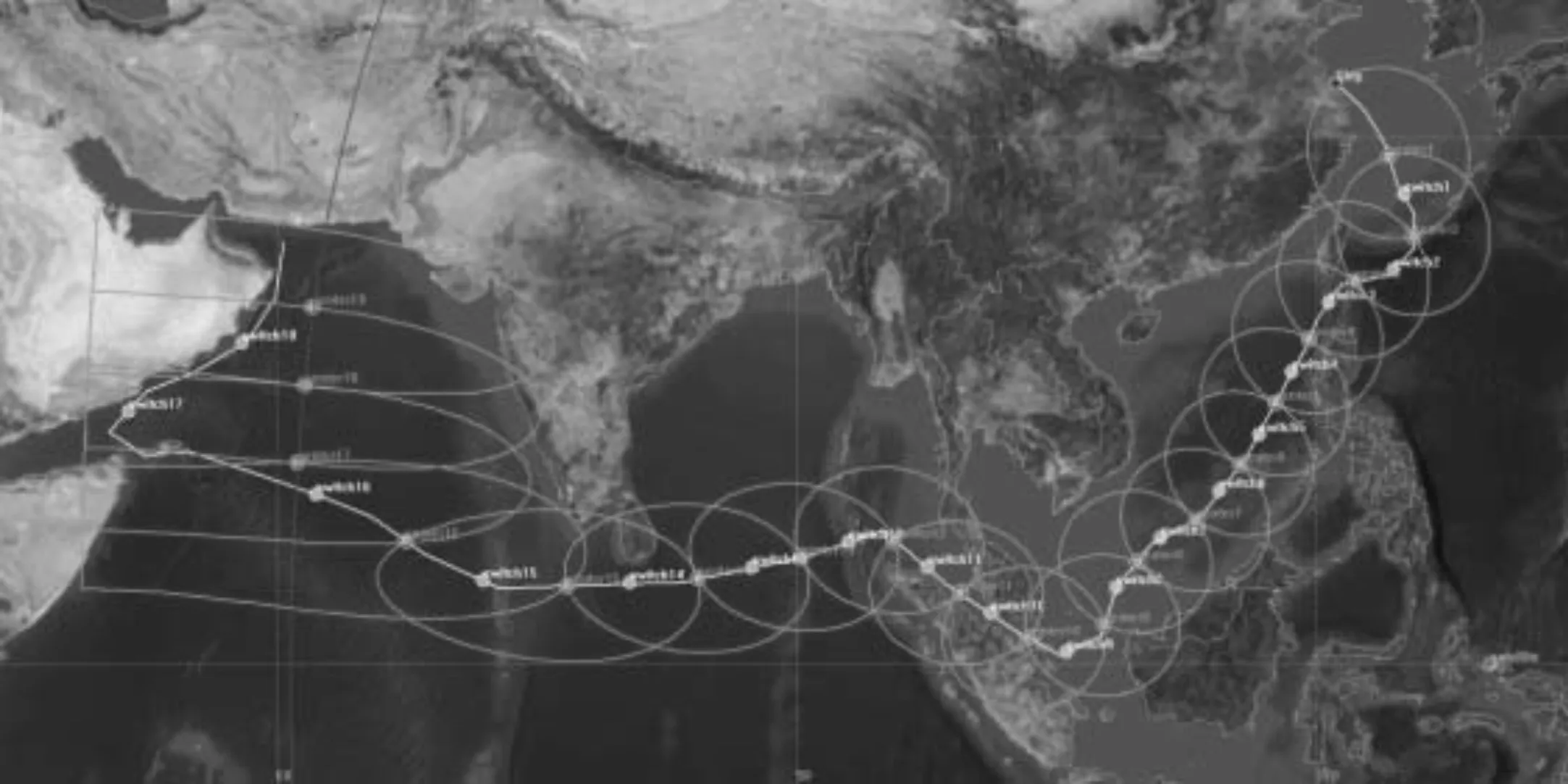
图5 半波束指向点波束移动示意图

图6为采用文中所提算法优化后的点波束指向示意图。算法中设置航线采样间隔为55km，搜索步长为0.5°，波束重叠区为100公里。比较两种指向方法可以看出，半波束指向方法共需移动点波束19次，而搜索优化方法仅需11次移动即可满足通信要求。可见，所提优化算法可以在保证通信需求的前提下，有效减少点波束移动次数，降低点波束天线转动损耗。尤其是对于远距离、大范围机动目标来说，其优化效果更加明显。

图6 搜索优化点波束指向示意图

5 结束语

本文针对卫星点波束在大范围、跨地域移动通信中的应用需求，提出了一种迭代搜索的点波束指向优化算法，阐述了关键步骤的实现方法，并对算法性能进行了仿真分析。仿真表明，通过将最大化当前点波束覆盖范围与设置点波束通信裕量两种方法相结合，可在满足通信质量要求的前提下有效减少点波束移动次数。与己有相关研究相比，所提算法可根据点波束天线性能和用户通信需求灵活设置天线转动限位、点波束调整裕量等参数，具有实用性强，适用范围广的优势。点波束的移动目标指向优化研究对于提高点波束天线使用效益，延长点波束天线在轨使用寿命具有重大意义。

[1] 刘刚, 吴诗其. 卫星蜂窝通信系统中的点波束设计[J]. 系统工程与电子技术，2004,26(2):157-159. LIU Gang, WU Shi-qi. Spot Beam Design in the Satellite based Cellular Communication System[J]. Systems Engineering and Electronics, 2004, 26(2): 157-159.

[2] 张旭，吴潜. 低轨卫星系统星载多波束天线点波束设计及优化[J].电讯技术, 2009,49(7):31-35.

ZHANG Xu, WU Qian. Spot Beam Design and Optimization of On-Board Multi-Beam Antenna for LEO Satellite Systems[J]. Telecommunication Engineering, 2009, 49(7):31-35.

[3] 高照照，杨慧．卫星锐波束天线指向算法及仿真[J]．中国空间科学技术，2008，28(2)：60-65. GAO Zhao-zhao， YANG Hui． Arithmetic and Analysis of Phased Array Scanning[J]． China Space Science and Technology，2008，28(2)：60-65.

[4] 李大耀．卫星沿轨道运动对地面覆盖带外沿轨迹的确定[J]．中国空间科学技术，1992，12(3)：19-26． LI Da-yao．An Investigation on Outer Boundary of the Earth’s Surface Band Region Covered with a Satellite in Orbital Motion [J]． Chinese Space Science and Technology，1992，12(3)：19-26.

[5] 翁慧慧．遥感卫星对地覆盖分析与仿真[D]．郑州：解放军信息工程大学，2006． WENG Hui-hui．Ground Coverage Analysis and Simulation of Remote Sensing Satellite[D]． Zhengzhou：The PLA Information Engineering University，2006．

[6] 郝文宇，潘冬，靖法. 卫星点波束天线的多目标指向优化研究[J]. 宇航学报，2012,12(33), 1788-1793. HAO Wen-yu, PAN Dong, JING Fa. Research on Optimization of Spot-Beam Satellite Antenna Pointing to Mulit-Targets[J].Journal of Astronautics, 2012, 12(33), 1788-1793.

[7] 鲍凯，徐慨，项顺祥. 基于STK的点波束覆盖分析与仿真[J]. 通信技术，2013，46(1)：17-19. BAO Kai, XU Kai, XIANG Shun-xiang. Analysis and Simulation of Spot Beam Coverage based on STK[J]. Communications Technology， 2013，46(1)：17-19.

[8] Thomas H.Cormen, Charles E.Leiserson.算法导论[M]. 北京：机械工业出版社，2013. Thomas H.Cormen, Charles E.Leiserson. Introduction to Algorithms[M]. Beijing: China Machine Press, 2013.

Moving-Target Pointing Optimization of Satellite Spot-Beam

HAN Xiang, GUO Xin-zhe, WU Ji-bo

(Unit 61096 of PLA, Beijing102300, China)

Due to its fairly small coverage and restricted rotating times by service life，satellite spot-beam antenna should be optimally designed in its pointing when used in wide-range communication with moving targets, thus trying to extend service life of this antenna while guarenteeing communication requirements. Through comprehensive consideration of some practical factors, such ad satellite visual range, rotating limit of spot-beam antenna spot-beam modulation overmeasure, a modified algorithm of spot-beam pointing based on iterative search is proposed. Simulation indicates that the proposed algorithm could effectively reduce the moving times of spot-beam antenna while satisfying the requirements of communication, and it also provides a high-efficient approach in spot-beam application, thus enjoying great value in engineering application.

spot-beam antenna; moving target; iterative search

10.3969/j.issn.1002-0802.2015.05.006

2015-02-13；

2015-04-14 Received date:2015-02-13；Revised date：2015-04-14

TN927

A

1002-0802(2015)05-0536-05

韩 湘(1975—)，女，博士，高级工程师，主要研究方向为卫星通信与卫星测控；

郭新哲(1978—)，男，本科，工程师，主要研究方向为卫星通信与卫星测控；

邬基博(1960—)，男，本科，工程师，主要研究方向为卫星通信。