短波宽带波形迭代均衡技术*

谢 枭，胡 飞，周 军，康弘俊

(西南通信研究所,四川 成都 610041)



短波宽带波形迭代均衡技术*

谢 枭，胡 飞，周 军，康弘俊

(西南通信研究所,四川 成都 610041)

短波宽带波形是现代短波通信的最新研究成果，短波信道时变多径传播效应会产生严重的码间干扰(ISI)，必须采用均衡技术消除ISI。迭代均衡技术(Turbo均衡)将信号检测技术和译码技术结合起来，比传统判决反馈均衡(DFE)技术具有更强抗ISI能力。研究了短波宽带波形Turbo均衡技术，提出了一种低复杂度的迭代检测方法用于短波宽带波形，仿真结果表明，在短波差信道条件下，Turbo均衡比DFE均衡的性能增益超过1.5 dB。

短波宽带波形；Turbo均衡；软输入软输出；对数似然比

0 引 言

短波(HF)通信是实现远距离、超视距军事通信和远洋运输通信的重要手段之一，在国际通信、防汛救灾、海难救援以及军事通信等方面具有重要作用。传统短波通信的信道带宽只有3 kHz，短波波形的典型代表是美国短波通信军事标准MIL-STD-188-110B[1]。110B采用相位调制(PSK)和最高64阶的幅度相位调制(QAM)等线性调制技术，以及卷积编码技术在3 kHz信号带宽内实现了有编码传输速率9 600 bit/s和无编码12 800 bit/s的短波通信，但110B波形对信道质量要求很高，在实际应用中难以达到2.4 kb/s稳定传输，其典型传输速率一般为600 b/s。因此，传统窄带短波通信只能用于传输话音和低速数据业务。随着现代社会信息化的发展，人们要求现代短波通信具有更高传输速率、更高传输可靠性、更强业务适应能力。为解决短波高速可靠通信问题，扩展短波通信信号带宽成为现代短波通信发展的一种必然趋势，美国在2011年提出了最大信号带宽为24 kHz的短波宽带波形标准规范110C[2]。

短波信道在时域和频域都是随时间变化的多径信道[3]，存在时域展宽、频域弥散、时变衰落和各种严重干扰。短波信道典型多径延迟为2 ms，极端情况下多径延迟可达到10 ms以上。因此，短波通信存在严重的符号间干扰(ISI)，必须采用有效的均衡技术克服ISI影响实现信号检测。判决反馈均衡器(DFE)[4]由于其实现复杂度低而且具有较好性能，在短波通信中得到广泛应用，但其信号接收均衡器和信道译码器是相互独立的。1995年Douillard等基于Turbo码的迭代译码思想，首次提出了用于信号检测的Turbo接收机[5]，Turbo接收机通过在信号检测器和信道译码器之间多次迭代获得了额外的迭代处理增益。

Turbo均衡器的常见算法包括：基于MAP算法Turbo均衡器，其性能最优但计算复杂度高，难以在多径延迟大的短波通信中得到应用。基于LISS算法Turbo均衡器利用有限状态机树查找机制来查找最佳路径[6]，其计算复杂度比MAP算法小，但仍不易于工程实现。Tuchler等提出了基于线性滤波和软干扰消除的Turbo均衡算法[7]，文献[8]提出了软判决反馈Turbo均衡算法。文献[9]则研究了采用高阶调制的软判决反馈Turbo均衡算法。前述Turbo均衡算法主要采用逐符号方式进行信号检测。文献[10]则提出了基于接收信号块处理的块判决反馈Turbo均衡算法。需要指出的是：上述Turbo均衡技术重点在于研究均衡算法本身，部分文献研究了Turbo接收机中信道估计和跟踪算法。

文献[11]则研究了短波窄带波形的线性滤波Turbo接收机技术，其研究表明Turbo接收机技术能够实现更好传输性能。基于单载波体制的短波宽带波形只是对窄带波形信号的带宽进行了扩展[2]，其它方面均一致，可将窄带波形的结论向宽带推广。

本文围绕短波宽带波形接收机设计需求，研究了短波宽带波形Turbo接收机设计，提出了一种便于工程实现的低复杂度、基于滤波器Turbo均衡算法，对比分析了Turbo接收机和判决反馈均衡接收机的性能。仿真结果表明：在短波差信道条件下， Turbo接收机比DFE接收机有超过1.5 dB的性能增益。

1 系统信号建模

本文采用的编码辅助Turbo均衡接收机的短波宽带通信系统模型如图1所示。

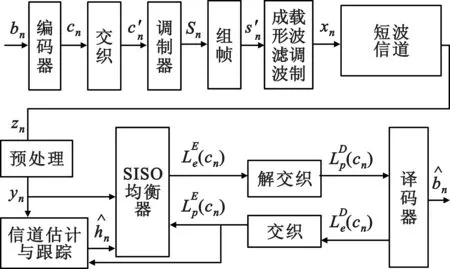
图1 系统信号框图

如图1所示，短波宽带波形将数据比特信息bn经过信道编码、交织和星座映射后调制符号sn，然后进行信号组帧，组帧信号通过成型滤波得到波形发射信号。波形信号经过短波信道传输后达到接收方，其离散基带采样信号z(n)在经过单音解调和时频同步处理后得到接收信号y(n)。接收信号y(n)经过编码辅助的软输入软输出(SISO)均衡器采用相干检测原理还原数据信息比特，其中：信道估计和跟踪采用波形同步头信号完成初始估计、利用波形训练信号以及数据硬解调和/或译码软信息来完成传输信道的时变性跟踪。

波形的基带信号参数如表1所示。信号带宽为12 kHz，其符号率为9 600 baud/s，其基带调制频率为6.3 kHz，波形接收采样率为76.8 kHz。

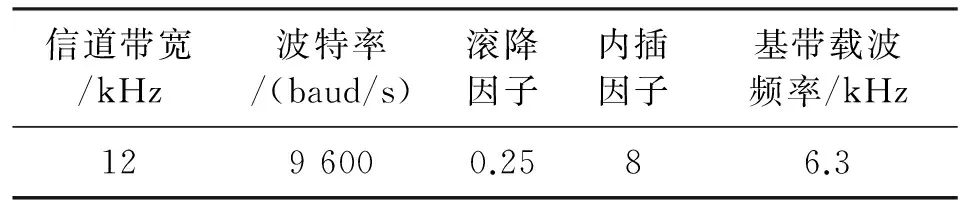
表1 信号基带参数

波形编码采用LDPC编码，对于不同传输速率所设计的编码码率和调制方式如表2所示。

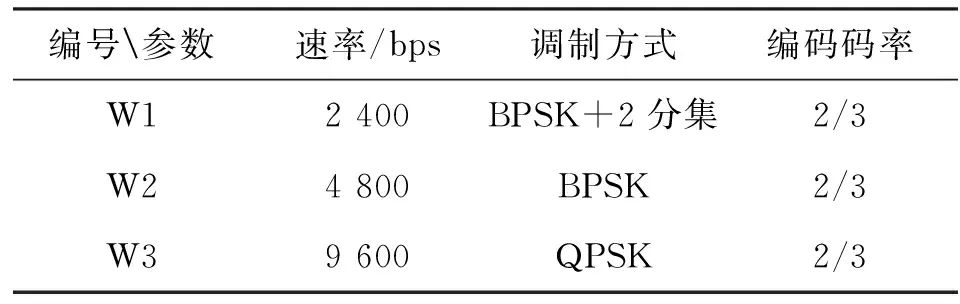
表2 编码和调制参数

波形离散基带信号可由下列数学公式(1)进行建模：

(1)

其中,x(n)表示发射信号；y(n)表示接收信号；w(n)表示均值为0、方差为σ2的加性高斯白噪声；{h0,h1,…,hL-1}表征了短波信道的离散等效多径传播效应，其多径长度为L。

短波信道是时变多径衰落信道，国际电信联盟无线通信组(ITU-R)推荐Watterson模型[12]作为短波通信测试信道建模，典型多径数目为两条延迟路径，每条路径的抽头分别独立地服从幅度的Rayleigh分布和相同的高斯衰减谱，其多径延迟时间和每条多径时变参数如表3所示。

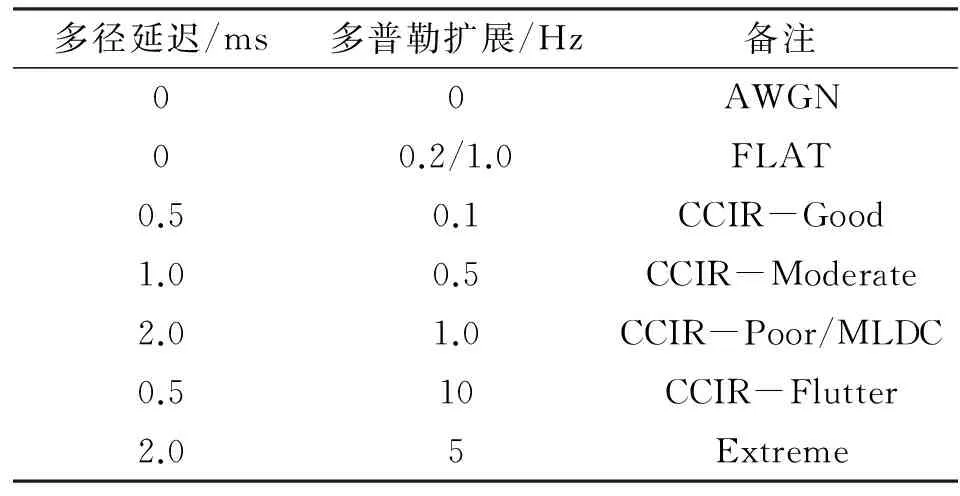
表3 短波信道典型参数

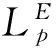
(2)

其中,Pr指的是当接收符号为yn时，编码比特为+1或-1的概率。

2 短波宽带波形迭代均衡技术

2.1 线性Turbo均衡算法

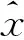
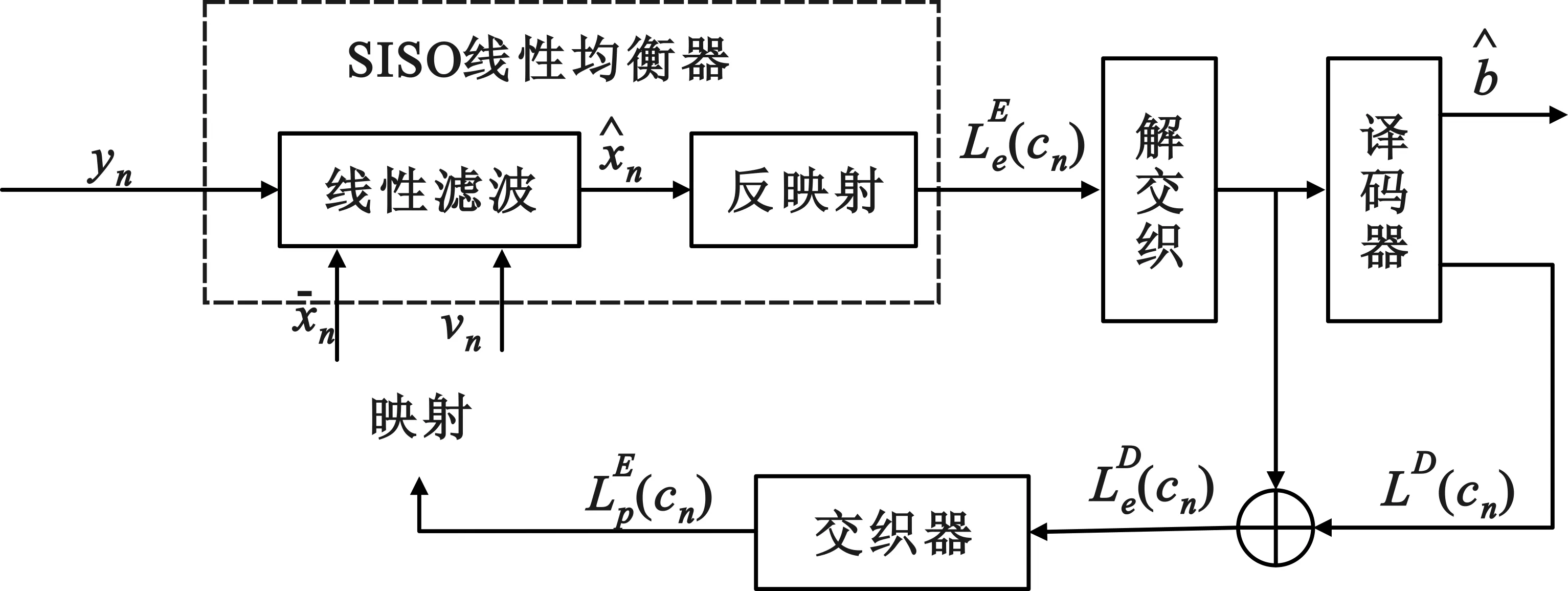
图2 Turbo-LE均衡器

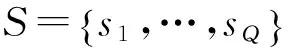
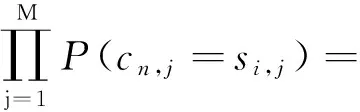
(3)

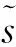
软信息与符号估计有映射与反映射的关系[7]，其中，根据软信息的定义，其映射成符号的方法只与调制方式有关。根据公式(3)，可以推导出具体转换算法见表4。

表4 软信息映射方法

(4)

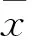
(5)

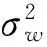
(6)

(7)

对于不同的调制方式，根据线性滤波均衡器的算法与结构，将符号估计计算成软信息的具体转换算法见表5。

表5 软信息计算方法

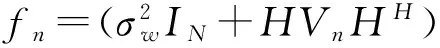
2.2 短波宽带波形Turbo均衡算法

短波宽带波形的符号率都是9 600 baud/s，波形数据帧结构中每个数据块长度固定为360个符号，可以计算出数据块的持续时间只有37.5 ms。而短波信道的多普勒扩展典型值为1 Hz,对应相干时间为1 s，远大于37.5 ms，为慢衰落信道，即在单个数据块传输时，信道条件变化不大。

因此，为了降低宽带波形接收机复杂度，可近似认为：数据块内每个符号不需要更新滤波器系数，即近似认为信道条件H在较短数据块(数据块长度K=360)内是固定不变的。因此，公式(6)可以改写为：

(8)

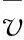
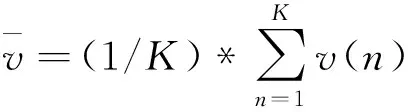
(9)

(10)

经上述处理，可以得到简化Turbo均衡算法LC(Low Complexity)-Turbo-LE。在同一个数据块内，滤波器的系数只需要更新一次，将运算量降为1/K。式(5)可改写为：

(11)

经过以上简化处理后，均衡器符号软信息计算方法如表6所示。

表6 简化后的软信息计算方法

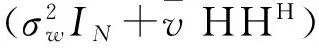
设R=HHH，乘积矩阵R的第i行第j列元素R(i,j)(i,j=0,1,…,N-1) 可表示为：

(12)

矩阵R为Hermite-Toeplitz矩阵，因此，只需要计算出矩阵R第一行的前L个元素，其他元素都可以不用计算，根据矩阵特征推出求出。此时矩阵乘法运算量由O(N*(N+L-1)3)降为O(L*(L+1)/2)。

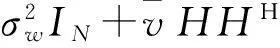
上述简化算法降低了波形均衡器运算量，可达到12 kHz带宽下短波宽带波形采用QPSK调制时的Turbo接收机工程实现需求。当波形带宽更大、传输速率更高时，由于波形采用64QAM、128QAM，甚至256QAM调制实现高速传输，此时Turbo接收机中均衡软信息的计算复杂度更高，还需要进一步简化上述Turbo接收机的计算复杂度。

3 性能仿真

对上述短波宽带波形Turbo接收机的性能进行了仿真对比分析，波形接收机分别采用了判决反馈均衡器和Turbo均衡器。波形信号为12 kHz带宽下传输速率为9 600 b/s，其调制方式为QPSK、编码码率为2/3。传输信道考虑无衰落的加性AWGN和多径衰落为2 ms、多普勒扩展为1 Hz的短波“差”信道。在短波“差”信道条件下，采用最小均方误差(LMS)算法对同步头信号进行初始信道估计，而短波信道时变性则采用LMS算法对每个数据块硬判决和训练信号进行信道跟踪。

图3给出了DFE均衡和Turbo均衡在AWGN信道下的性能对比图，可以看出：Turbo接收机和DFE接收机性能接近，而且不同迭代次数的Turbo接收机性能基本相同。

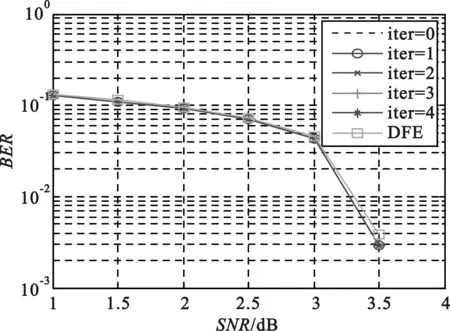
图3 AWGN信道下性能对比

图4给出了短波“差”信道(CCIR-Poor)下的DFE接收机和Turbo接收机的性能对比，本次测试只验证了DFE和迭代0-4次的性能。从结果中可以看出无迭代Turbo接收机性能比DFE性能差，这是因为无迭代Turbo接收机采用了线性均衡器；经过译码器反馈的一次迭代后，Turbo接收机性能超过了DFE接收机，而且随着迭代次数增加，其性能改善更明显，在10-3误码率条件下，4次迭代Turbo接收机性能比DFE接收机性能改善了1.5 dB。

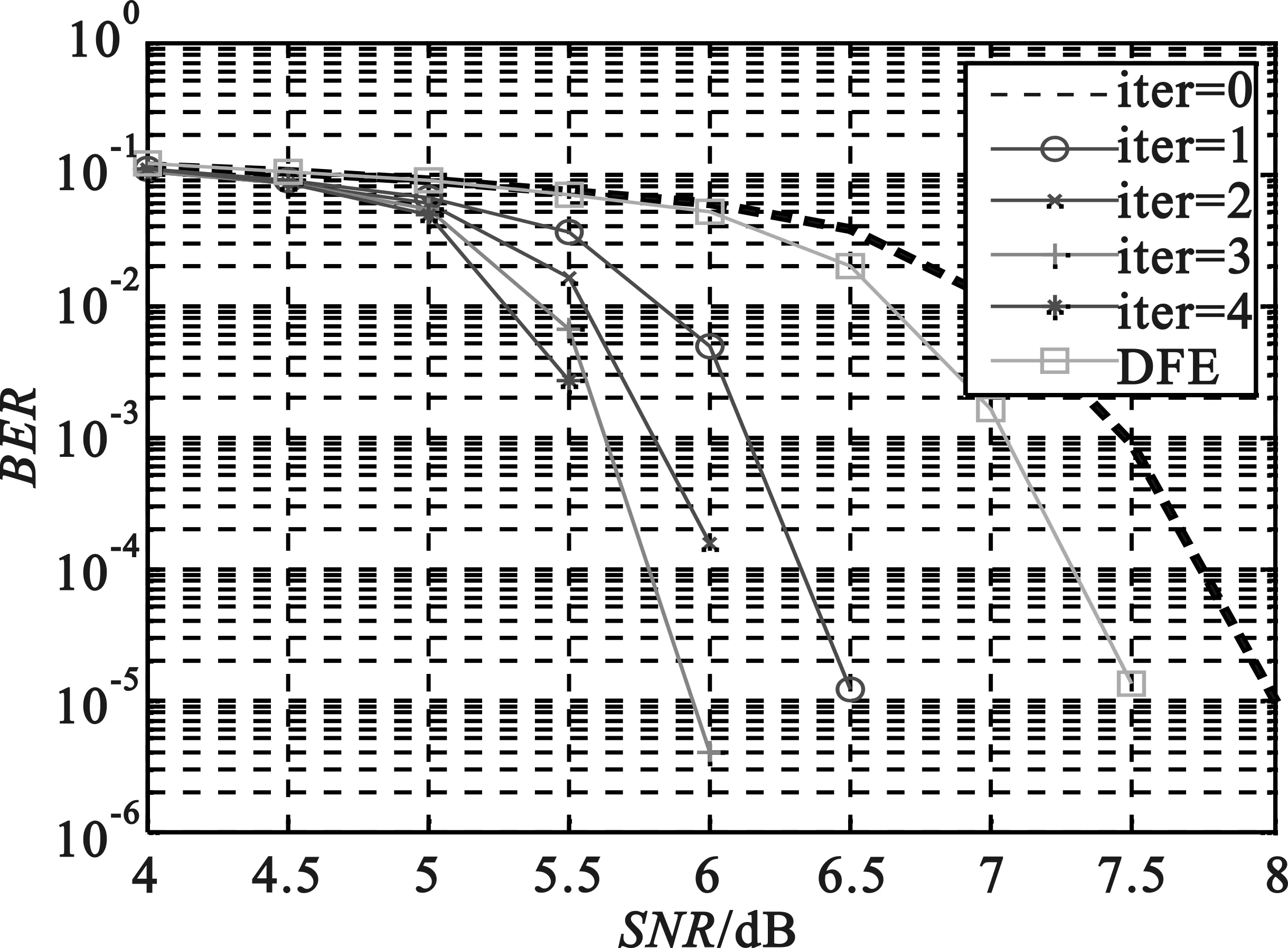
图4 CCIR-Poor信道下性能对比

综合以上仿真结果可以看出，在AWGN信道条件下，Turbo接收机能够实现DFE接收机相同性能；但是在短波“差”信道条件下，Turbo接收机在4次迭代后得到了1.5 dB的性能增益。

4 结 语

短波宽带波形需要一种性能优良信号检测方法来解决信号接收问题，采用编码辅助迭代均衡技术的Turbo接收机是一种可行方案。但Turbo接收机一个主要缺陷是其计算复杂度较高，工程实施难度较大。本文对此问题进行了研究，提出了一种实用化的短波宽带波形LDPC码基Turbo接收机方案，有效提升了短波宽带波形的性能。

需要指出的是：本文提出的Turbo接收机性能增益优势还不明显。在短波“差”信道条件下，信道存在时变性和实际接收机存在同步误差，准确跟踪信道变化对波形性能有着重要的影响，预期在后续通过优化信道估计和跟踪算法，进一步提升短波宽带波形Turbo接收机的性能。

[1] DoD. MIL-STD-188-110B, Interoperability and Performance Standards for Data Modems[S].USA: Department of Defense, 2000.

[2] DoD. MIL-STD-188-110C, Interoperability and Performance Standards for Data Modems[S].USA: Department of Defense, 2011.

[3] 刘 洋,朱立东.一种改进的窄带短波信道模型及仿真实现方法[J].通信技术,2009,42(05):1-4. Liu Y, Zhu L D. An Improved Narrowband High Frequency Channel Model and SimulationAlgorithm[J]. Communications Technology, 2009,42(05):1-4.

[4] Kaleh G K. Channel Equalization for Block Transmission Systems[J]. IEEE Journal on Selected Areas in Communications, 1993,13(1):110-121.

[5] Douillard C, Jezequel M, Berrou C, et al. Iterative correction of inter-symbol interference: turbo equalization [J]. European Trans Telecomm, 1995,6(5):507-511.

[6] Kuhn C, Hagenauer J. Turbo equalization for channels with high memory using a list-sequential (LISS) equalizer[C].in Proceedings of the International Symposium on Turbo Codes & Related Topics,Brest,France,2003:9-13.

[7] Tüchler M, Singer A C, Koetter R. Minimum mean squared error equalization using a priori information[J]. IEEE Trans Signal Processing, 2002,50(03):673-683.

[8] Lopes R R, Barry J R. The soft-feedback equalizer for turbo equalization of highly dispersive channels[J]. IEEE Trans Communications, 2006,54(5):783-788.

[9] Lou H. Low-complexity soft-decision feedback turbo equalization for multilevel modulations[D]. Missouri University of Science and Technology, 2012.

[10] Wu J. Improved BDFE using a prioriinformation for turbo equalization[J]. IEEE Trans On Wireless Communications,2008,7(1):233-240.

[11] Otnes R. Improved receivers for digital high frequency communications: iterative channel estimation, equalization, and decoding (adaptive Turbo equalization)[D]. Norwegian University of Science and Technology,2002.

[12] Watterson C C, Juroshek J R, Bensema W D. Experimental confirmation of an HF channel model[J].IEEE Transactions on Communication Technology,1970,18(6):792-803.

[13] 徐世良.常用算法程序集[M].北京:清华大学出版社，2004:96-98. Xu S L.Commonly used algorithm and program collections[M]. Beijing: Tsinghua University Press, 2004:96-98.

Turbo Equalization for Wideband HF Waveforms

XIE Xiao, HU Fei, ZHOU Jun, KANG Hong-jun

(Southwest China Institute of Communications, Chengdu Sichuan 610041, China)

Wideband HF (High-Frequency) waveform is the latest research achievement of modern HF communication. Time-varying multi-path propagation of HF channel would result in high ISI (Inter-Symbol Interference), and this ISI must be eliminated by equalization technique. Iterative equalization technique (turbo equalization), in combination of signal detecting technique and decoding technique, enjoys a stronger ability of resisting ISI than traditional DFE (Decision Feedback Equalization) technique. This paper discusses the equalization technique for wideband HF waveform, proposes a low-complexity iterative detection method for wideband HF waveform. Simulation results show that the performance gain of turbo equalization is 1.5dB over that of DFE equalization in CCIR-Poor channel.

wideband HF waveform；turbo equalization；soft input soft output；log-likelihood ratio

10.3969/j.issn.1002-0802.2015.05.004

2015-01-06；

2015-04-11 Received date:2015-01-06；Revised date：2015-04-11

国防科技重点实验室基金项目(No.9140C02010814C02006)

Foundation Item:Science and Technology Foundation of State Key Laboratory(No.9140C02010814C02006)

TN911

A

1002-0802(2015)05-0524-06

谢 枭(1987—)，男，硕士研究生，主要研究方向为通信信号处理、短波通信；

胡 飞(1970—)，男，博士，高级工程师，主要研究方向为纠错编码、通信信号处理、短波通信；

周 军(1984—)，男，硕士，助理工程师，主要研究方向为无线通信中的数字信号处理；

康弘俊(1977—)，男，硕士，高级工程师，主要研究方向为短波通信、通信信号处理、通信系统设计。