橡胶蠕变对圆筒式粘弹阻尼器长度的影响分析

张 昊，覃海鹰，吴明忠

(中航工业直升机设计研究所，江西 景德镇 333001)



橡胶蠕变对圆筒式粘弹阻尼器长度的影响分析

张 昊，覃海鹰，吴明忠

(中航工业直升机设计研究所，江西 景德镇 333001)

基于硅橡胶的本构关系，建立了线性模型和非线性模型两种粘弹性材料的蠕变分析模型，通过四剪块硅橡胶试样蠕变试验对建立的线性模型和非线性模型进行评估，确定了适合粘弹性阻尼器的蠕变分析方法，在此基础上完成了不同形变下的硅橡胶相对蠕变量分析，得出了粘弹性阻尼器有限蠕变结论，并就此结论分析计算出某型机实际外场使用时粘弹阻尼器的蠕变情况。

橡胶蠕变；非线性模型；长度

0 引言

旋翼阻尼器是直升机旋翼系统的关键部件，其主要功能是为旋翼桨叶的摆振提供阻尼，保证直升机有足够的稳定性裕度，从而防止“地面共振”。粘弹阻尼器是现代直升机旋翼系统上运用最多的阻尼器之一，其本身结构简单、可靠性高、维护性好等优点能大大降低直升机使用成本并减少停机时间[1]。粘弹阻尼器的工作原理是利用粘弹材料剪切变形时产生很大的内阻尼来提供所要求的阻尼。但是由于其本身由金属和硅橡胶复合而成的结构特点，硅橡胶材料的性能就决定了阻尼器性能。而作为橡胶材料，其自身的蠕变是不可避免的，特别是在动态工作条件下，其蠕变更会呈现加速现象。目前，圆筒式粘弹阻尼器在实际外场使用过程中出现了工作一段时间后自然伸长的情况，由于阻尼器的伸长量无法预测，维护人员只能通过调节阻尼器两端的关节轴承来恢复最初的工装长度，同时也并不清楚阻尼器长度的变化趋势，因此有必要进行橡胶蠕变对粘弹阻尼器长度的影响的研究。

1 蠕变模型的建立

硅橡胶属于典型的粘弹性材料，其力学行为介于弹性固体和粘性流体之间，可简化用弹簧和粘弹串联或并联的机械模型进行表述。本文通过建立两种不同的模型：标准线性固体模型、非线性模型，进行对比分析。

1.1 标准线性固体模型

标准线性固体模型[2]，是基于弹簧和阻尼器的微分型本构关系，主要由Kelvin模型(由一个弹簧和一个阻尼器并联组成)与一个弹簧串联组成, 见图1。其中E2，η1为Kelvin模型的弹簧弹性模量和阻尼器的阻尼系数，E1为串联的弹簧弹性模量，根据本构关系将本模型的一般形式表达为：

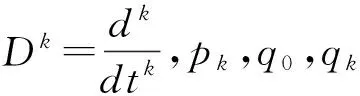
图1 标准线性固体模型

针对图1所示的标准线性固体模型，进行简化得出本构方程：

式中，p1,q0,q1与E1，E2，η1为相关的材料参数。

在准静态条件下，恒应力σ(T)可以写成σ(t)=σ0H(t)=R(t)J(t),其中，H(t)为单位阶跃函数，J(t)为蠕变柔度，因此对式(1)进行拉氏变换:

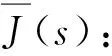
再进行拉氏逆变换得出蠕变柔度J(t)表示为：

所以，根据线性粘弹性理论，在标准线性固体模型中，蠕变相对量R(t)与应变γ0之间存在的关系得出：

1.2 非线性蠕变模型

由于硅橡胶材料在实际工作中的蠕变行为表现出强的非线性相关性，用线性模型在预估硅橡胶的蠕变模型时存在一定误差，为了优化模型，需在前面提出的线性模型的基础上，引入一个新的非线性模型，此非线性模型是在考虑不同应力大小作用下基于单轴作用下蠕变的多重积分本构关系提出的[3]。

首先，对粘弹性材料作用任一剪切应力τ(t)，其一维蠕变型的多重积分非线性本构关系表示为：

其中，J1，J2，J3为硅橡胶的蠕变函数,等式右边为硅橡胶的线性响应项和非线性响应项(后面的多重积分为应力的高次项)。

对于式(7)，先设τ(t)=τ0H(t)，再对两边进行求导得出：

其中，H(t)为单位阶跃函数，δ(t)为狄拉克函数。

由于硅橡胶蠕变过程中，线性项与非线性项的影响程度的不一致性，引入影响系数κ，代入式(7)得出：

简化式(9)得出非线性模型通用的蠕变相对值为：

式中，f1(t)，f2(t)，f3(t)为材料的柔度函数，由于硅橡胶蠕变行为表现出明显的非线性，这里为了将应力在整个蠕变过程中的影响体现出来，将非线性项分解出两项:强应力相关性项和弱应力相关项，则将(10)整理为：

其中，等式右边第一项为材料的线性响应项，f1(t)采用1.1节中标准线性固体模型的蠕变柔量表达式；等式右边后两项为材料的非线性响应项，等式右边第二项主要反映蠕变应变的强应力相关性，其中τ0n2表示应力对材料蠕变应变的非线性影响，f2(t)假定与标准线性固体模型蠕变柔度f1(t)有类似之处：

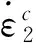
其中a3，n3为模型参数，再将式(13)对时间进行积分：

其中C为常数，将式(11)等式右边第三项采用和(14)类似的形式：

此项反映了材料稳态蠕变应变率基本不随应力变化的特点。因为当n3非常小时，该项的应力敏感性将很小，F(σ0，t)则表示为时间的线性函数。

再根据应力应变关系τ=Gγ，得出非线性模型的蠕变相对量的计算公式：

R(t)=κ1Gγ0f1(t)+κ2(Gγ0)n2a2(1-

2 蠕变模型的评估

2.1 蠕变试验

取四块橡胶试样，由长度为25mm，宽度为20mm，厚度为4mm的尺寸相同的橡胶片组成，每个橡胶片的两个相对最大面分别于与这四块宽度相同、长度适宜的刚性板对应面相互粘合，形成一个对称的双夹层结构。在刚性板两自由端中心位置采用适宜的方法可与试验机的夹具配合相连，试验如图2所示。

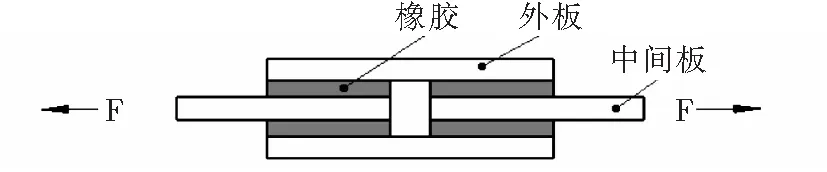
图2 硅橡胶蠕变试验加载方式

试验中的剪切应变γ按γ=d/c来计算，其中，d：单个试样的形变，c：单个试样橡胶片的长度。本文进行了两组为期15天的10%形变和20%形变情况下的剪切拉伸蠕变试验(10%、20%形变d的计算：d10=0.1×c,d20=0.2×c)，得出硅橡胶蠕变数据见表1。

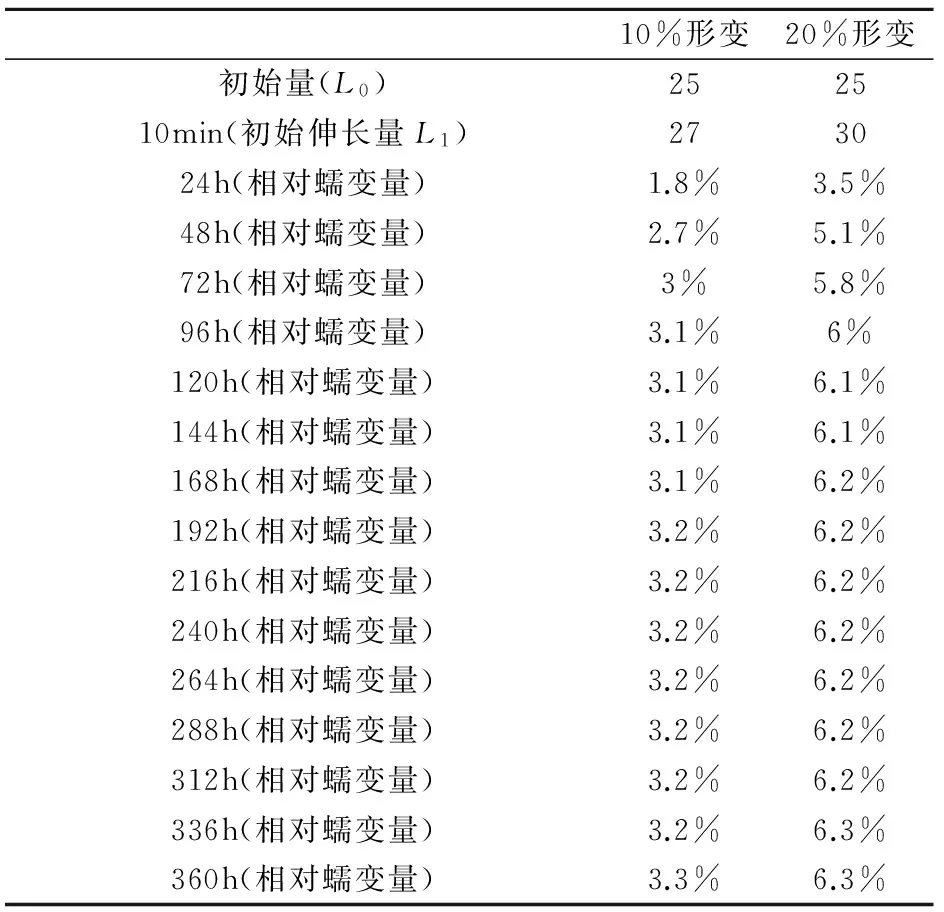
表1 硅橡胶蠕变数据表

(试验中的蠕变计算：设L0为原始标线长度(单个试块的长度)，L1为加载10分钟后的长度，Li为i*24小时后长度，则蠕变按下式计算：i*24小时后的相对蠕变量：(Li-L1)/L0×100%；)

2.2 线性和非线性模型蠕变行为的评估

对于线性模型和非线性模型的行为的模拟，根据前面2.1节给出的两组试验数据，利用matlab对式(6)和式(16)进行参数模拟，拟合得出:

10%形变下线性模型的参数：

q0=2.95,q1=145,p1=2

10%形变下非线性模型的参数：

n2=0.04,a2=0.004,c2=0.1,n3=0.01,

a3=0.0000015,k1=0.55,k2=0.3,k3=0.15

根据两个模型的参数做出线性模型、非线性模型和试验数据对比图，见图3。

图3 硅橡胶在10%形变下线性模型、

为了进一步验证前面提到的线性、非线性模型的准确性，根据10%形变下的两个模型模拟参数计算得出20%形变下的线性、非线性曲线，图4为两种模型计算得出结果同试验曲线的对比图。

对比图3和图4不难发现，对于线性模型在两个不同形变情况下模拟出的结果与试验所得曲线相差较大，而非线性模型在两种情况下计算得出的值都比较接近试验值。所以，本文所提出的非线性模型对硅橡胶蠕变行为的评估较标准线性固体模型更为准确。

图4 硅橡胶在20%形变下线性模型、

3 某直升机粘弹性阻尼器蠕变量分析

根据前文的结论，非线性模型对硅橡胶蠕变行为的评估预言值较好。针对某直升机的粘弹阻尼器，其结构基本参数为：G=0.304MPa，R1=23mm，R2=39mm，L=268mm。(其中R1为内筒半径，R2为外筒半径，L为橡胶层长度)，利用非线性模型的模型参数：

n2=0.4,a2=0.01,c2=0.1,n3=0.01,

a3=0.0000015,k1=0.45,k2=0.38,k3=0.17

计算得出不同形变γ下的硅橡胶相对蠕变量曲线见图5。

图5 非线性模型下相对蠕变量同形变量关系图

从上图可以看出粘弹阻尼器在长期小形变量(低于28%)下蠕变量随形变量增加而增加，呈现一个正增长的趋势。当长期形变量超过30%，阻尼器的蠕变趋于平稳，即超过这个量之后阻尼器的形变可以得到恢复，最大恒久蠕变量为8.3%。

根据外场实际情况，作出单个粘弹阻尼器停机状态下的位置示意图如图6，其中A、B为两端杆端关节轴承处于中距时的位置，C、D为支臂低距-7°时逆时针旋转的位置，E、F为支臂向下搭至下挥限动环时杆端关节轴承的位置，A1，B1，C1，D1，E1，F1分别对应A、B、C、D、E、F在Z轴(为旋翼轴)的投影。

图6 粘弹阻尼器位置示意图

设A，B，C，D，E，F点的坐标(xa，ya，za)，(xb，yb，zb)，(xc，yc，zc)，(xd，yd，zd)，(xe，ye，ze)，(xf，yf，zf)，根据几何位置关系：

将各点坐标代入，为了简化计算，这里将O点坐标设为，化简得出：

|EF|=

则在停机状态下，粘弹阻尼器的静拉伸量ΔL：

ΔL=|EF|-|AB|=5.5mm

因此，根据非线性模型计算得出对于粘弹阻尼器在停机状态静拉伸量为5.5mm下(折合应变为5.5/268=2.1%)最终相对蠕变量为1.2%，即最终蠕变量为3.2mm。

4 结论

1) 采用非线性蠕变模型评估粘弹性阻尼器的蠕变误差较线性固体模型的要小，接近真实试验数据，更适合进行蠕变评估。

2) 在长期形变量小于28%范围内，粘弹性阻尼器的相对蠕变量随拉伸形变量增加而加大，当长期形变量超过30%后蠕变量逐渐趋于平稳；

3) 蠕变达到约8.3%前，粘弹性阻尼器的蠕变会一直持续下去，当蠕变达到约8.3%后，接近纯弹性体，产生的变形基本上可以恢复。

4) 外场使用粘弹阻尼器的最终相对蠕变量为1.2%，即最终蠕变量为3.2mm。

[1] 黄文俊，李满福.直升机旋翼设计技术应用现状及发展综述[J]. 航空制造技术， 2011.

[2] 杨挺青．粘弹性理论与应用[M]．北京：科学出版社，2004.

[3] 高 庆，林 松.丁基橡胶粘弹性材料的非线性蠕变本构描述[J]. 应用力学学报， 2007.

Analysis of the Influence of Rubber Creep on the Length of Cylindrical Viscoelastic Damper

ZHANG Hao, QIN Haiying, WU Mingzhong

(China Helicopter Research and Development Institute, Jingdezhen, 333001)

This paper built a linear model and a non-linear model that both analyzing the creep behavior based on the constitution relation of the silicon rubber. Then, evaluated the linear model and non-linear model through a four-cut pieces of silicone rubber creep test, and determined the suitable creep analysis method for the viscoelastic damper. On this basis, we completed the analysis of the relative creep deformation for the different deformation, so that it’s coming to the conclusion that the creep’s deformation is limited, and analyzed and calculated the creep of the viscoelastic damper of one helicopter in the actual field based on the conclusion.

rubber creep; non-linear model; length

2015-01-27

张 昊(1992-)，男，安徽安庆人，硕士，助理工程师，研究方向为旋翼系统设计。

1673-1220(2015)03-006-05

V255+.3；V250.3

A