基于LS-DYNA的滑橇起落架落震分析及二次开发

陶周亮，方建义，张 梅

(中国直升机设计研究所，江西 景德镇 333001)



基于LS-DYNA的滑橇起落架落震分析及二次开发

陶周亮，方建义，张 梅

(中国直升机设计研究所，江西 景德镇 333001)

滑橇起落架在着陆过程中通过结构变形来吸收着陆功量而不产生结构破坏，因此迫切需要开发一套高效可靠的直升机滑橇起落架落震分析方法。基于显式动力学和接触算法，在考虑旋翼升力的影响和机身与弓形梁连接点处的弯矩传递问题的基础上，建立滑橇起落架落震分析模型。为提高仿真分析效率，搭建由二次开发软件、ANSYS和LS-DYNA组成的落震分析系统。在两种工况下对滑橇起落架进行了落震仿真分析，仿真结果与试验结果吻合较好，表明了滑橇起落架落震仿真分析方法的有效性。

直升机；滑橇起落架；落震；显式动力学；二次开发

0 引言

滑橇起落架结构简单，易于加工和维护。现代轻型直升机多采用滑橇式起落架[1]，在直升机着陆过程中通过前、后弓形梁的变形来吸收着陆能量，前后弓形梁会产生很大的塑性变形而要求结构不产生破坏。

在滑橇起落架着陆冲击的过程中，滑橇受到地面的垂直冲击载荷和地面的摩擦力载荷。弓形梁产生垂直地面的垂向位移和沿地面方向的侧向位移，随着载荷增大，弓形梁的各个截面依次由弹性状态进入塑性状态。滑橇起落架的着陆性能计算是一个求解滑橇在动载荷作用下的几何非线性、材料非线性和状态非线性的问题，难度较大且不可能用解析方法进行求解[2]。目前国内外主要采用数值分析方法。贝尔直升机公司的Cheng-Ho Tho等[3]对带圆角的矩形截面弓形梁进行简化，完成了滑橇起落架的落震分析。黄生月、张绍仪等[4]采用“位移-增量迭代法”来处理滑橇起落架在坠毁过程中吸收着陆功量这一弹塑性、大变形问题。为防止地面共振，滑橇起落架前弓形梁上通常会安装减振器，黄生月、彭宗梁等[5]在前面的工作基础之上进行了带减振器的滑橇式起落架耐坠毁研究。对于这种复杂的冲击碰撞过程，以非线性有限元基本理论和接触算法为基础的非线性有限元软件可以得到较好的结果[6]。本文在LS-DYNA中对滑橇起落架进行落震仿真分析，将计算结果与试验对比以验证准确性。为了克服在设计过程中模型反复修改带来的重复仿真分析并提高效率，本文基于LS-DYNA和VC++进行滑橇起落架落震分析的二次开发，该研究对滑橇起落架的设计具有非常重要的工程实际应用价值。

1 滑橇起落架落震分析方案

滑橇起落架的落震分析方案由三部分组成：二次开发软件、ANSYS和LS-DYNA。二次开发软件基于VC++[7]开发，其功能为调用ANSYS、修改K文件以及调用LS-DYNA进行仿真分析。其中LS-DYNA为滑橇起落架落震分析方案的计算核心。

滑橇起落架落震分析流程如图1所示，通过在二次开发软件中输入建模参数、实常数参数、材料参数和试验参数，自动生成APDL代码，代码包含了建模、创建材料、网格划分、加载、初始速度以及K文件生成等等。通过创建进程的方式调用ANSYS运行APDL代码，生成供LS-DYNA执行的K文件。软件对成功生成的K文件进行修改，释放机身与弓形梁连接点处绕航向的转动自由度。软件调用LS-DYNA运行成功修改后的K文件进行滑橇起落架的落震仿真分析。

由于在ANSYS中添加constrained_nodal_rigid_body约束时，无法释放连接点处的自由度，通常是在LS-PrePost中完成自由度释放，这也是二次开发软件两次分别调用ANSYS和LS-DYNA的原因。通过对滑橇起落架落震进行参数化，二次开发软件根据输入参数快速进行滑橇起落架落震的建模，极大地提高了落震分析的效率和质量，尤其是对于设计的反复修改导致的迭代分析。

图1 滑橇起落架落震分析流程图

2 非线性有限元计算理论

非线性方程的求解方法分两种：隐式方法和显式方法。非线性有限元中一般采用Newton-Raphson的隐式求解方法，它是将非线性方程线性化进行求解，通过不断迭代，在每次迭代步中修改刚度矩阵，最终达到平衡。而显式方法主要指中心差分法。

2.1 显式积分

对于非线性方程：

式中：U为位移矩阵，P(t)为外力向量矩阵，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵。

LS-DYNA采用显式中心差分法来进行时间积分[8]，在已知0, …,tn时间步解的情况下，求解tn+1时间步的解，运动方程为：

式中：Fint(tn)为内力矢量，H(tn)为沙漏阻力。

tn+1时刻的速度和位移由下面公式求得：

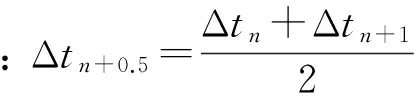
集中质量矩阵M为对角矩阵，很容易进行求逆，运动方程的求解是非耦合的，不需要组成总体刚度矩阵和对刚度矩阵求逆，与隐式方法对比，大大节省了存储空间和计算时间。

2.2 接触算法

LS-DYNA处理接触一般采用三种不同的算法：动力约束法、分配参数法和对称罚函数法。对称罚函数法为缺省使用算法[9]，其原理是每一时先检查各从节点是否穿透主表面，没有穿透则不对该从节点做任何处理。如果穿透，则在该节点与主表面间，主节点与从表面引入一个较大的界面接触力，大小与穿透深度、接触刚度成正比，称为罚函数值。其物理意义相当于在其中放置一系列法向弹簧，限制穿透，接触力的表达式为：

式中：K为接触界面刚度，δ为穿透量。

LS-DYNA中接触的摩擦系数由下式计算可得：

式中：fd为动摩擦系数，fs为静摩擦系数，β为指数衰减系数，Vrel为接触表面的相对速度。

3 有限元模型

考虑到仿真分析的计算效率，采用梁单元beam161对滑橇起落架的前、后弓形梁和滑管进行建模，而机身几乎不产生吸能变形，故采用mass166来表示。通过约束constrained_nodal_rigid_body将机身质量点和前、后弓形梁的四个连接点进行刚体连接。在冲击过程中，对单个弓形梁而言，地面支撑力和摩擦力产生的弯矩在两端传递到弓形梁的中部。而刚体连接会限制弯矩的传递，需释放四个连接点绕航向的转动自由度，在四个连接点处建立局部坐标系，把RRFLAG置为1。试验台采用壳单元shell163和刚体材料建模，限制其平动和转动的六个自由度。有限元模型如图2所示。

图2 滑橇起落架落震有限元模型

在整个落震冲击的过程中，滑橇起落架是吸收着陆功量的主要部件，在大的着陆功量下，前、后弓形梁会进入塑性变形，以Hughes-Liu非线性梁单元模型对前后弓形梁进行建模，前、后弓形梁总共采用了70个梁单元。为了模拟弓形梁进入塑性的状态，弓形梁的材料采用双线性等向强化(BISO)。考虑到滑管有可能进入塑性变形状态，故采用与弓形梁相同的材料模型，滑管的有限元模型由30个梁单元组成。试验台在落震冲击中产生的变形很小，所以在建模时将试验台考虑为刚体，由100个壳单元组成，刚体单元几乎不参与迭代计算，给刚体划分网格时适当增加网格数量并不会增加计算时间，却有助于提高主从面接触计算的准确性。

滑管和试验台之间的接触采用点面接触contact_nodes_to_surface，定义滑管上所有的节点为从面，试验台上所有的节点为主面，输出滑橇和试验台之间的接触界面力(rcforc)。

而实际落震过程中，直升机旋翼处于旋转状态，其产生的旋翼升力是落震冲击过程中不可忽视的关键影响因素，旋翼产生的升力如下式所示：

式中：L为旋翼产生的升力，KL为旋翼升力系数，一般取2/3，m为机身质量，g为重力加速度。

在有限元模型施加重力场载荷时，考虑旋翼升力的影响下等效的重力加速度为：

式中：Kres为直升机升力卸载影响系数[10]，取1/3。

4 计算结果与试验对比

在质心处定义飞机的有效落震重量，为缩短仿真时间，不考虑自由落体阶段，从滑管接触试验台前一刻开始仿真，仿真时间为0.12s。为验证仿真结果的准确性，在动摩擦系数为0.25时，对两种工况(落震高度为64mm和落震高度为204mm)进行仿真，并与试验数据进行对比。

4.1 工况一(落震高度为64mm)

图3所示为落震高度为64mm时重心处垂直压缩量曲线，曲线在同一时刻达到峰值，仿真结果的峰值略大于试验结果。两条曲线的上升以及下降保持一致，仿真与试验结果整体吻合度较好。

图3 重心处垂直压缩量曲线(落震高度为64mm)

图4所示为落震高度为64mm时滑管与试验台之间的接触力曲线，经轻微光滑处理的仿真结果曲线带有略微的毛刺感。仿真结果的峰值略大于试验结果的峰值，仿真结果的上升及下降均比试验结果要快，这主要是试验中存在的阻尼影响所致， 除此之外，两种结果非常接近。

图4 滑管与试验台之间的接触力曲线(落震高度为64mm)

4.2 工况二(落震高度为204mm)

图5所示为落震高度为204mm时重心处垂直压缩量曲线，在整个落震过程中，仿真结果的峰值与试验结果的峰值接近，两种结果的吻合度非常好。

图6所示为落震高度为204mm时滑管与试验台之间的接触力曲线， 两者的峰值接近。相对落震高度为64mm的结果来说，曲线在峰值附近“滞留”的时间较长，这是由于滑橇进入了塑性之后变得相对较“软”。从整体上来看，两种结果吻合度较好。

图5 重心处垂直压缩量曲线(落震高度为204mm)

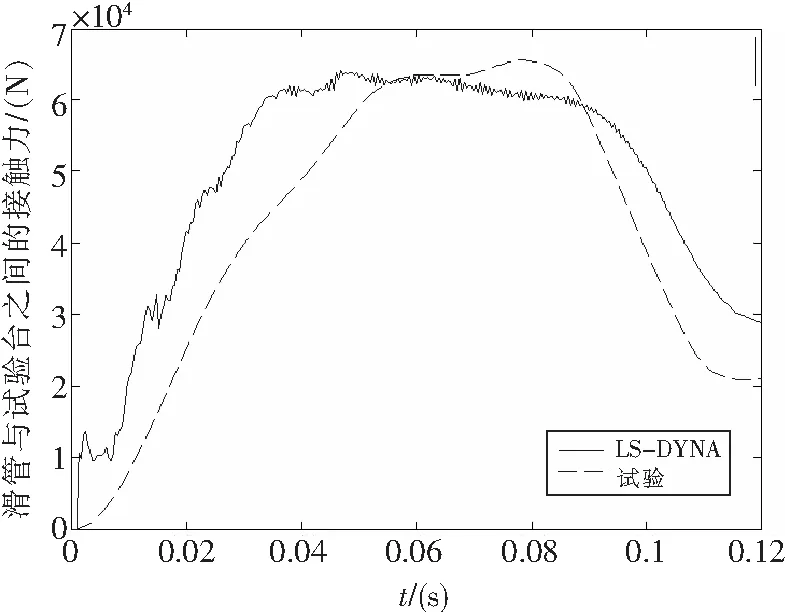
图6 滑管与试验台之间的接触力曲线(落震高度为204mm)

4.3 结果对比分析

表1所示为仿真结果与试验结果的对比，从表中数据可以看出，工况二下的仿真结果比工况一略微更贴近于试验结果。相对于滑管与试验台之间的接触力峰值，重心处的垂向压缩量峰值的仿真结果与试验结果的误差要更小，都在2%以内。而滑管与试验台之间的接触力峰值的仿真结果与试验结果的误差最大值为5.83%，处于合理的范围内。总体上，两种工况显示仿真结果与试验结果非常接近，表明落震分析方法准确有效。

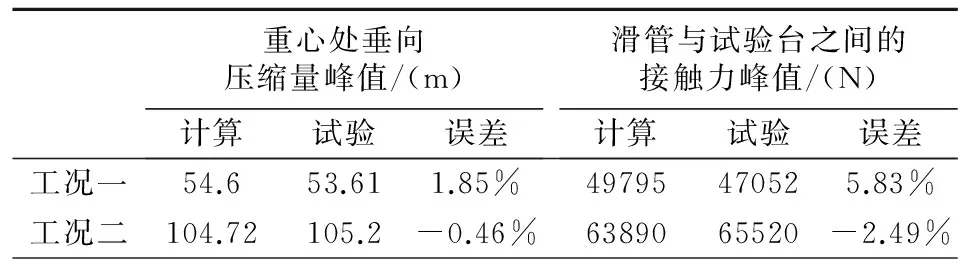
表1 仿真结果与试验结果对比

5 结论

1) 建立了滑橇起落架落震仿真模型，模型中考虑了旋翼升力的影响，考虑到弓形梁弯矩的传递问题，释放了机身与弓形梁连接点处绕航向的转动自由度，模型更加符合实际情况。

2) 采用梁单元对弓形梁和滑管进行建模，采用壳单元对试验台进行建模，把试验台考虑为刚体，在不影响精度的前提下大大提高了仿真分析效率。

3) 仿真结果与试验结果对比显示，仿真结果与试验结果吻合度很好，表明本文提供的仿真分析方法能有效地对滑橇起落架落震进行计算。

4) 由二次开发软件、ANSYS和LS-DYNA组成的滑橇起落架落震分析方案能快速提高落震计算效率及质量，具有较大的工程实际应用价值。

[1] 杨俊严. 直升机载荷手册[M]. 北京：航空工业出版社, 1991.

[2] 王新敏. ANSYS工程结构数值分析[M]. 北京：人民交通出版社, 2007.

[3] Tho C H, Sparks C E, Sareen A K. efficient helicopter skid landing gear dynamic drop simulation using LS-DYNA[J]. Journal of the American Helicopter Society, 2004, 49(4): 483-492.

[4] 黄生月, 张绍仪, 王志荣. 耐坠毁滑橇式起落架的设计研究[J]. 中国航空科技文献,1986.

[5] 黄生月, 彭宗梁, 王仁良, 等. 带减震器的滑橇式起落架耐坠毁研究[J]. 中国航空科技文献,1992.

[6] 王俊峰, 张志谊. 基于LS—DYNA的冲击试验机碰撞分析[J]. 噪声与振动控制，2007(6): 10-12.

[7] Prata S. C++ Primer Plus(第五版)中文版[M]. 北京：人民邮电出版社, 2005.

[8] 赵海鸥. LS-DYNA动力学分析指南[M]. 北京：兵器工业出版社, 2003.

[9] Hallquist J 0. LS-DYNA Theory Manual[Z].1998．

[10] 高泽迥. 飞机设计手册：第14分册[M].北京：航空工业出版社, 2002.

Analysis and Secondary Development of Skid Landing Gear Shock Based on LS-DYNA

TAO Zhouliang, FANG Jianyi, ZHANG Mei

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

Skid landing gear absorb landing energy by the way of structural deformation in the landing process without structural failure, a efficient and reliable analysis method of skid landing gear shock is urgently needed. Considering the influence of rotor lift and the transfer problem of bending moment on the joints of the fuselage and the skid based on explicit dynamics and contact algorithm, the analysis model of skid landing gear shock was established. In order to raise the efficiency of simulation analysis, an analysis system of shock was established with secondary development software, ANSYS and LS-DYNA. The shock of skid landing gear was analyzed in two working conditions The simulation results were in good agreement with test results, which showed that the provided simulation analysis method of skid landing gear shock in this paper was effective.

helicopter; skid landing gear; shock; explicit dynamics; secondary development

2015-05-21

陶周亮(1989-)，男，江西九江人，硕士，助理工程师，主要研究方向：起落架设计。

1673-1220(2015)03-025-04

V214.1+3；V226

A