电动汽车驱动电动机的三维温度场仿真分析

田玉冬，　王　潇，　张舟云

(1. 上海电机学院 汽车学院， 上海 200245； 2. 上海理工大学 机械工程学院，

上海 200093； 3. 上海电驱动股份有限公司 技术中心， 上海 200240)



电动汽车驱动电动机的三维温度场仿真分析

田玉冬1,2，王潇1,2，张舟云3

(1. 上海电机学院 汽车学院， 上海 200245； 2. 上海理工大学 机械工程学院，

上海 200093； 3. 上海电驱动股份有限公司 技术中心， 上海 200240)

摘要:针对电动汽车驱动电动机工作温升过高的问题，利用计算流体动力学方法对驱动电动机进行额定工况下的三维稳态温度场仿真计算，分析得出了电动机三维全域的温度场分布情况及温升极值区域；通过电动机实验平台，将实验数据与数值计算结果进行对比，验证了仿真计算的正确性，最后总结了电动汽车驱动电动机内部温度场的分布规律以及影响电动机温升的因素。

关键词:驱动电动机； 三维温度场； 有限元法； 稳态

近年来，随着电动汽车驱动电动机功率密度不断增加、电动机额定电流以及转矩密度的提高，常引起电动机工作时内部温升过高；且由于电动汽车驱动电动机安装空间狭小、使用工况复杂，也使得其温度场分布不均、内部局部区域温升过高。电动机工作时温升过高将限制其极限功率，且长时间处于高温运转状态也将极大地降低电动机的使用安全性。因此，电动汽车驱动电动机的温度场计算已成为国内外学者的热点研究领域之一。如文献[1]中采用了等效热传导方式处理电动机定、转子铁芯与其间气隙复杂的对流换热过程，并对电动机的相关散热系数进行研究。文献[2]中分析了电动机内部热源的传热形式和传热路径。文献[3-4]中采用节点热网络法，运用传热方程对电动机节点的平均温度进行计算。文献[5]中利用电磁场与流场耦合分析的方法对感应电动机极限温升进行了研究。然而，由于电动机温度场计算情况复杂，目前均只采用了相应的温度场简化模型。如，有的电动机温度场模型只考虑了定子铁芯区域，有的模型则只考虑了转子铁芯区域。另外，采用温度场节点热网络计算方法虽然简单直观、便于工程计算，但该方法也只能计算出热网络中所设节点的平均温度，无法对电动机温度场进行全面分析。

基于电动机内部的传热规律，本文运用计算流体动力学(CFD)方法对电动汽车驱动电动机整体进行了温度场计算，分析了电动机全域的温度分布情况及局部最热区域，并对样机进行了相应的实验测试，验证了数值计算的正确性。

1电动机的基本参数和求解区域

1.1　基本参数

本文以一台额定功率为21kW的电动汽车驱动电动机为研究对象，并根据电动机的设计尺寸建立了其热计算的求解域模型。表1给出了样机的基本参数。实验测试样机及实验测试平台如图1所示。

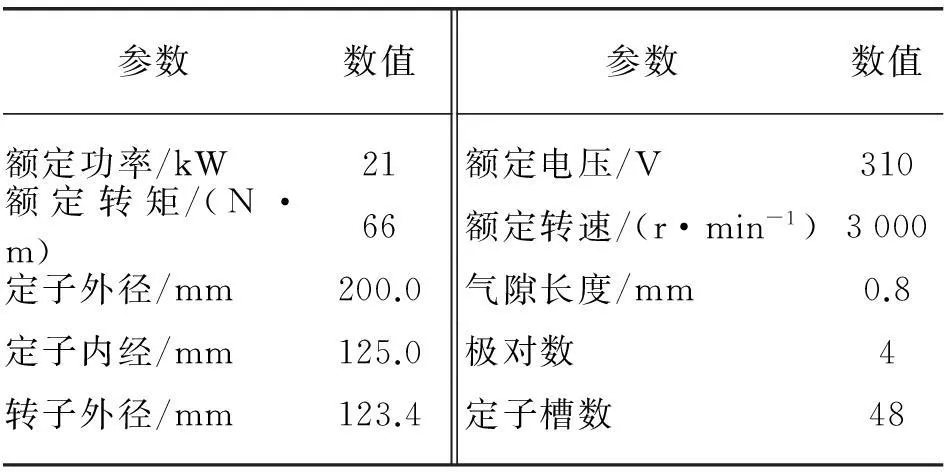
表1　驱动电动机样机参数Tab.1　Parameters of the prototype motor

图1　实验测试样机与测试平台Fig.1　General view of prototype motor and　experimental bench

1.2　求解区域

根据驱动电动机轴向对称、轴向周期性重复的结构特点，本文给出了驱动电动机1/4的结构模型如图2所示。

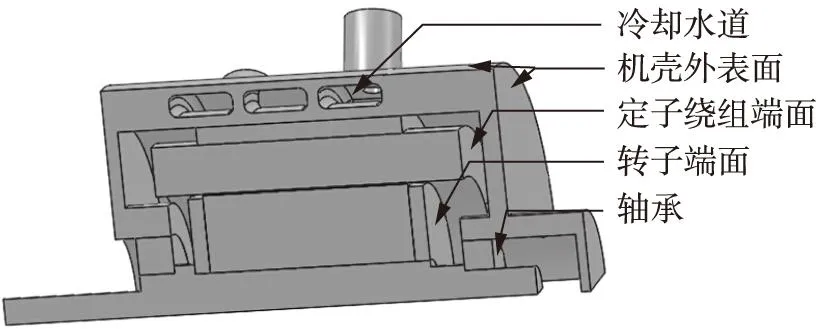
图2　实验测试样机结构模型Fig.2　Physical model of the prototype motor

驱动电动机温度场求解区域模型如图3所示。图中，A1为水道出水口；A2为水道入水口；A3为机壳外表面；A4为水道；A5为定子铁芯；A6为定子槽；A7为定、转子间气隙；A8为转子铁芯；A9为永磁体。

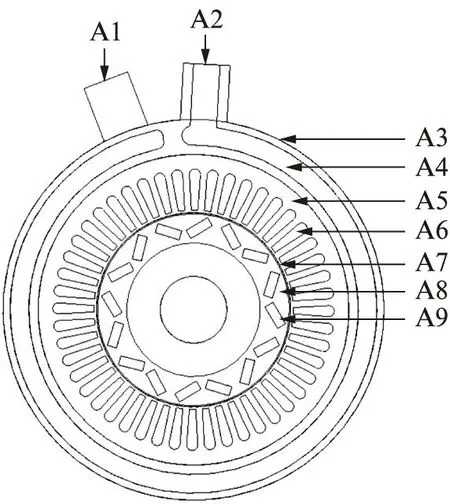
图3　求解温度场区域模型Fig.3　Model for solving the temperature field

同时，为了简化电动机温度场的分析过程，仿真计算时假定了以下条件[6-8]： ① 电动机在圆周方向的冷却条件相同，忽略外部风速对于电动机轴向方向冷却的影响；② 忽略定子绕组端部的趋肤效应；③ 定子槽内绝缘纸和绝缘漆的绝缘性能相同，无空气泡存在；④ 用静止流体的等效导热系数来描述气隙的对流换热。

2电动机温度场的数学传热模型

电动机运行时，内部三维温度场符合傅里叶导热定律[9-12]。基于傅里叶导热定律以及能量守恒方程可以推导出电动机内部导热微分方程为

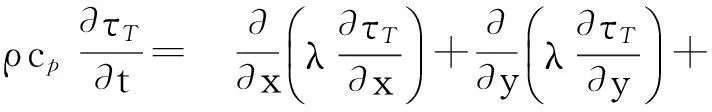
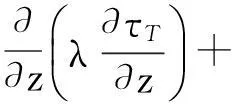
(1)

式中，ρ为物质的密度；cp为物质的比热容；t为时间；τT为温度场梯度；λ为物质的导热系数；φv为物体内热源；x、y、z为方向。

3电动机散热系数的确定及损耗计算

根据传热学基本理论，电动机本身可看成一个内部有源传热体，其主要的传热形式为接触固体间的热传导、固体与流体之间的热对流[13-14]。另外，中小型功率电动机的辐射热量很小，可忽略不计。

3.1　散热系数的确定

样机的定、转子气隙长度为0.8mm。当转子旋转时，可用有效导热系数来等效气隙与定、转子间流动空气的热交换能力。气隙等效导热系数为

λeff=0.0019η-2.908 4Re0.461 4·ln(3.333 61η)

(2)

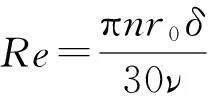
当电动机运行时，定子绕组产生绕组铜耗，为电动机热源[15]。绕组产生的热量一部分通过定子铁芯传递到机壳，被机壳水路中的冷却介质带走；另一部分则由绕组端部与机内空气的热对流传递出去。定子绕组端部对流换热系数为

(3)

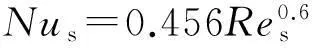
转子铁芯在旋转运行时，其端面与机壳腔内空气形成热对流。转子铁芯将转子域一部分的热量通过气隙、定子区域传递至冷却水路，另一部分的热量则由转子铁芯两侧端面的对流换热方式散热。转子端面的对流换热系数为

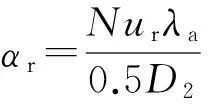
(4)

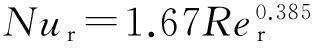
电动机机壳与定子外圆紧密接触，机壳外表面的对流换热系数由经验公式[16]给出：

αjk=9.73+14v0.62

(5)

式中，αjk为机壳外表面的对流换热系数；v为机壳外部风速。

综上计算得到：λeff=26mW/(m·K)，αs=46.2W/(m2·K)，αr=60W/(m2·K)，αjk=9.73W/(m2·K)。

3.2　热边界条件计算

本文考虑了电动机的绕组铜耗与铁芯损耗，并将其作为电动机的热源；利用Maxwell软件对电动机进行电磁计算分析，得到在额定运行状态下电动机损耗值，并根据其相应的生热部件的体积可以计算得到对应的生热密度，计算结果如表2所示。

表2　生热部分的热密度Tab.2　Volumetric power of heat section

4热仿真定义

4.1　材料定义

电动机材料的热性能参数如表3所示。其中，聚芳砜纤维箔用于隔离定子铁芯和绕组线圈的接触。

4.2　加载

仿真时，将电动机热载荷以热密度的形式施加到电动机各生热部件上。驱动电动机的铜耗为416W，铁耗为1357W。

根据电动机的传热形式，对其机壳外表面施加空气自然对流换热条件，对冷却介质与水道的接触面、绕组外端面、定子铁芯端面施加强制对流换热条件。设置环境温度为22℃，冷却介质初始温度为60℃。

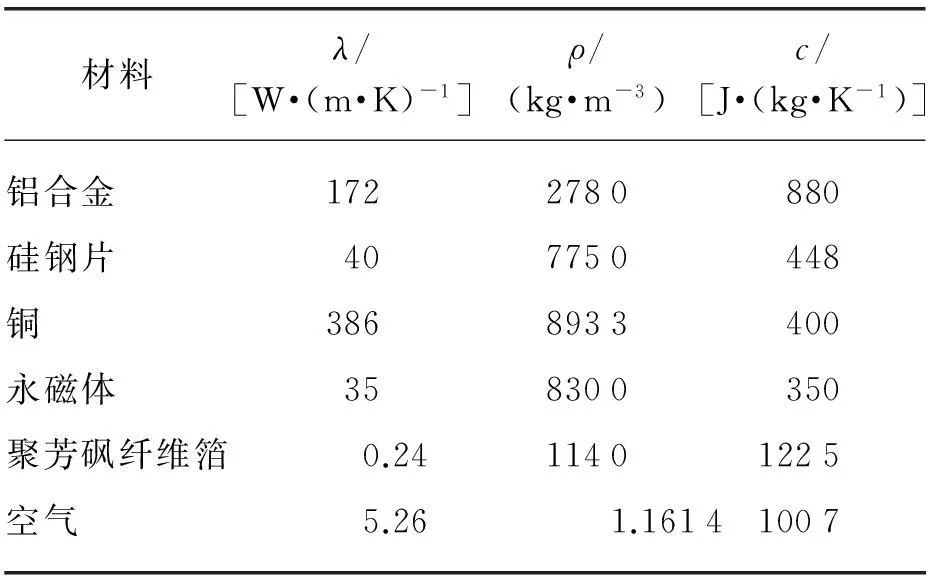
表3　驱动电动机材料热性能参数Tab.3　Thermal parameters of materials inthe traction motor

5仿真结果及分析

通过仿真计算得到该驱动电动机的三维温度场分布云图。图4给出了电动机各热源的温度分布图。图5给出了电动机整体温度场分布图。

由图4、5可见，电动机整体温度场由气隙明显分隔为转子区域和定子区域，转子区域的温度要高于定子区域。电动机整体的最高温度为 117.21℃，出现在转子域的永磁体中部；定子绕组的最高温度为104.5℃，出现在绕组端面的一侧；定子铁芯的最高温度为100.69℃，出现在定子齿部与气隙接触区域；转子铁芯的最高温度为117.08℃，出现在转子铁芯中部区域。由此可见，电动机的主要热源位于定子绕组端部和永磁体中部，由于环形螺旋水路置于机壳中部，散热条件较好，故在该水路的有效覆盖范围内温度较低；而在散热条件不好的区域，如绕组端部以及散热路径较远的永磁体则温度较高。定、转子气隙两侧的温差达到近18℃，表明气隙的隔热效果较强。

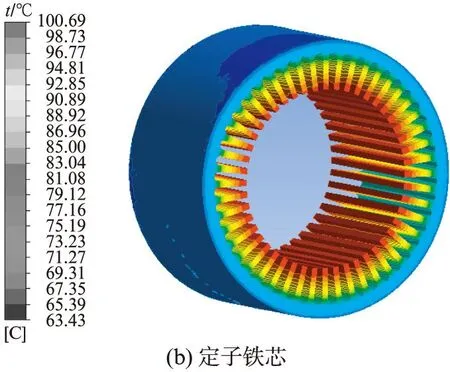
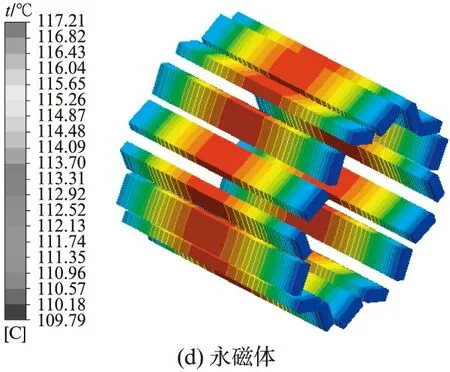
图4　驱动电动机各热源的温度分布

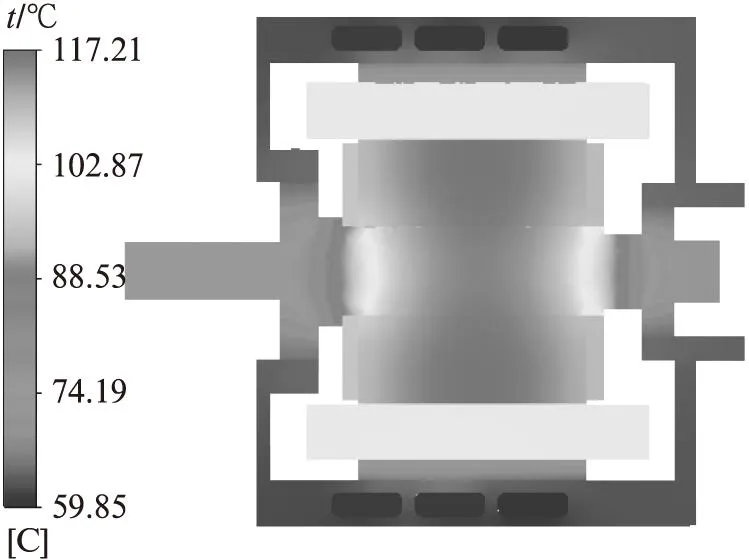
图5　驱动电动机整体温度场分布Fig.5　Temperature distribution in the traction motor

对电动机进行温度场测试，在其内部的关键位置埋置多根热敏电阻线，分别位于绕组端部、定子槽底部、转子内的永磁体处，测得热阻电阻实测温度值。表4给出了热敏电阻实测的温度值以及仿真计算出的关键位置温度值。由表可见，电动机稳态的有限元计算值和实测值接近，表明仿真计算结果是可取的。

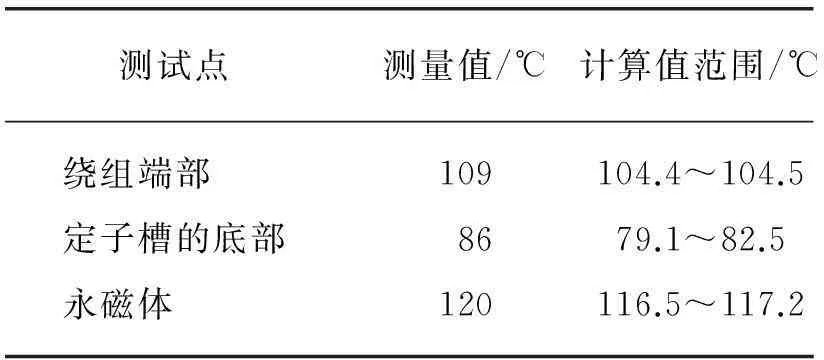
表4　有限元计算值与测量值Tab.4　FEM and measured data

6结论

本文针对一台额定功率为21kW的电动汽车驱动电动机进行研究，对电动机进行了三维全域温度场仿真计算与实验。通过研究分析可得到以下结论：

(1) 当电动机温度场达到稳态热平衡时，由于定、转子间气隙的导热效果较差，使转子区域和定子区域的温度差明显，转子区域的整体温度高于定子区域。

(2) 转子区域内径向温度分布均匀，最高温度集中于永磁体中部；定子区域内轴向温度变化小，最高温度位于绕组端部一侧。表明电动机运行时，定子绕组端部和永磁体中部为易产生热量的过热区域。

(3) 由于转子区域材料的导热性能较好，永磁体和转子铁芯的温度差很小。

(4) 气隙的隔热效应对电动机转子域的温升起着关键的作用。

参考文献：

[1]李青青,黄勤,杨立，等.永磁同步电动机水冷系统散热参数分析与热仿真[J].机械设计与制造,2014(4)： 188-191.

[2]邰永,刘赵淼.感应电动机全域三维瞬态温度场分析[J].中国电机工程学报,2010,30(30)： 114-120.

[3]Staton D A,Cavagnino A.Convection heat transfer and flow calculations suitable for electric machines thermal models[J].IEEE Transactions on Industrial Electronics,2008,55(10)： 3509-3516.

[4]Huang Yunkai,Zhu Jianguo,Guo Youguang.Thermal analysis of high-speed SMC motor based on thermal network and 3-D FEA with rotational core loss included[J].IEEE Transactions on Magnetics,2009,45(10)： 4680-4683.

[5]Marignetti F,Colli V D,Coia Y.Design of axial flux PM synchronous machines through 3-D coupled electromagnetic thermal and fluid-dynamical finite-element analysis[J].IEEE Transactions on Industrial Electronics,2008,55(10)： 3591-3601.

[6]Boglietti A,Cavagnino A,Lazzari M,et al.As implified thermal model for variable-speed self-cooled industrial induction motor[J].IEEE Transactions on Industrial Application,2003,39(4)： 945-952.

[7]谢颖,辜承林.笼型感应电动机三维全域温度场计算[J].中国电机工程学报,2012，32(36)： 96-101.

[8]李翠萍,裴宇龙,梁培鑫，等.水冷感应电机不同运行状态下的稳态温度场分析[J].微电机,2013,46(3)： 1-5.

[9]Driesen J,Belmans R J M,Hameyer K.Finite element modeling of thermal contact resistances and insulation layers in electrical machines[J]. IEEE Transactions on Industrial Applications,2001,37(1)： 15-20.

[10]Shenkman A L,Chertkov M.Experimental method for synthesis of generalized thermal circuit of poly phase induction motors[J].IEEE Transactions on Energy Conversion,2000,15(3)： 264-268.

[11]李伟力,李守法,谢颖，等.感应电动机定转子全域温度场数值计算及相关因素敏感性分析[J].中国电机工程学报,2007,27(24)： 85-91.

[12]和伟超,吴建华.电动汽车驱动电机水冷系统的设计及其温度场分析[J].轻工机械,2013,31(5)： 19-25.

[13]Staton D,Boglietti A,Cavagnino A.Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors[J].IEEE Transactions on Energy Conversion,2005,20(3)： 620-628.

[14]Hameyer K,Driesen J,De Gersem H,et al.The classification of coupled field problems[J].IEEE Transactions on Magnetics,1999,35(3)： 1618-1621.

[15]孔晓光,王凤翔,刑军强.高速永磁电机的损耗计算与温度场分析[J].电工技术学报,2012,27(9)： 166-173.

[16]孙建鑫,孙永兴,王玉彬.嵌入式永磁同步电动机二维稳态温度场分析[J].微特电机,2013,41(6)： 24-26.

Analysis of Three-Dimensional Temperature Field Simulation ofElectric Vehicle’s Traction Motor

TIANYudong1,2,WANGXiao1,2,ZHANGZhouyun3

(1. School of Automobile, Shanghai Dianji University, Shanghai 200245, China; 2. College of

Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093,

China; 3. Technical Center,Shanghai Edrive Co., Ltd, Shanghai 200240, China)

Abstract:To deal with serious temperature rise in traction motors of electric vehicles (EV), a computational fluid dynamics (CFD) method is used to calculate the 3D temperature field in the rated operating state. The temperature distribution and the hottest regions in the traction motor are obtained. A platform is set up to verify the simulation results by comparing them with experimental results. Conclusions about the heat transfer characteristics and factors that influence the motor temperature field are given.

Key words:traction motor; three-dimensional temperature field; finite element method; steady state

文献标志码:A

中图分类号:TM 301.4

文章编号2095 - 0020(2015)01 -0013 - 06

作者简介：田玉冬(1968-)，男，博士，教授，主要研究方向为复杂工业系统控制,E-mail： tianyd@sdju.edu.cn

基金项目：国家自然科学 资助(51377104)；上海市闵行区科技项目资助(2013MH109)

收稿日期：2014 - 12 - 16