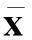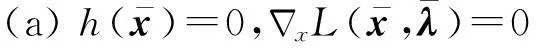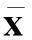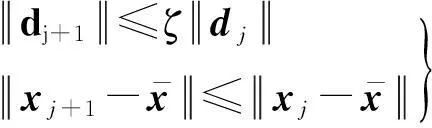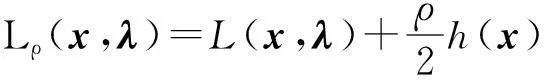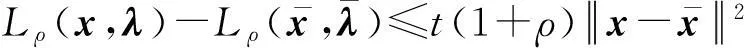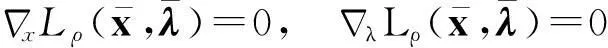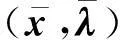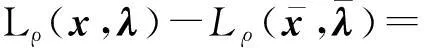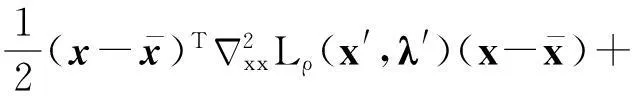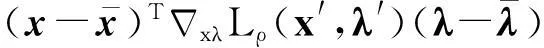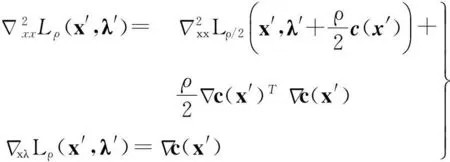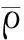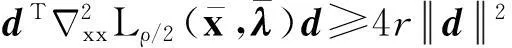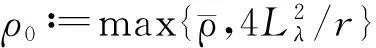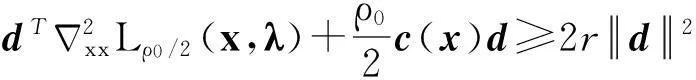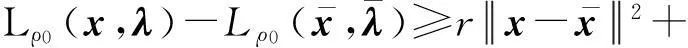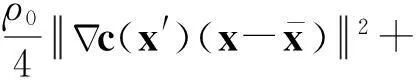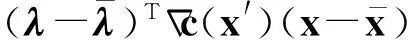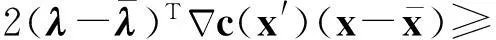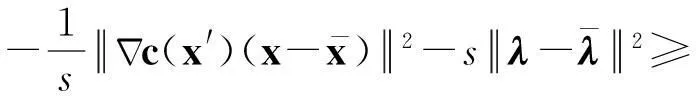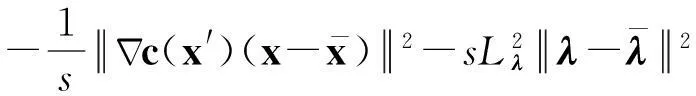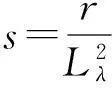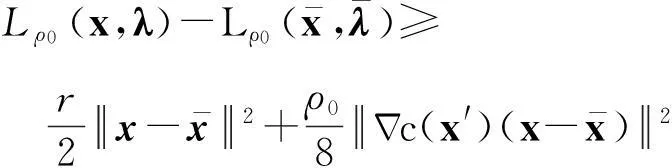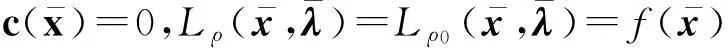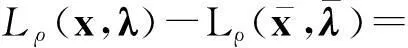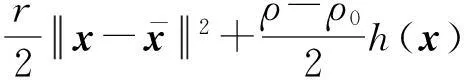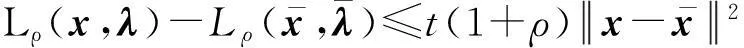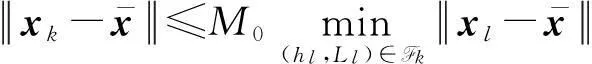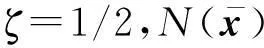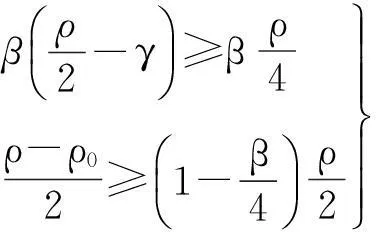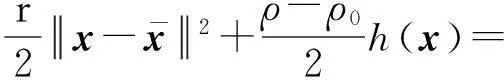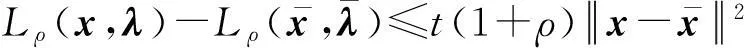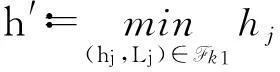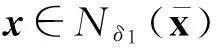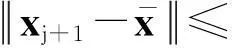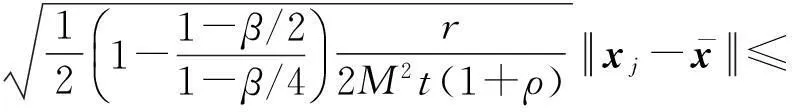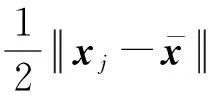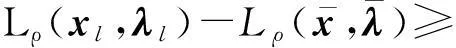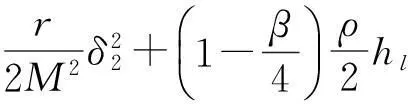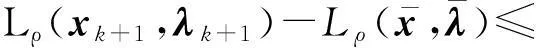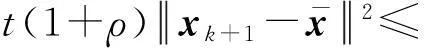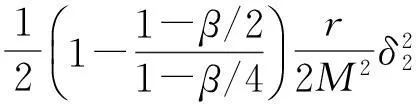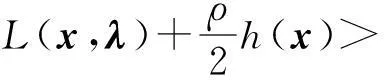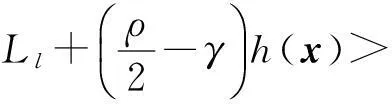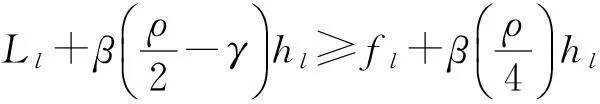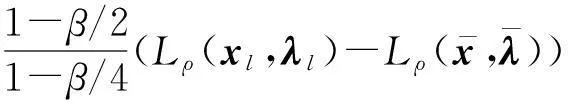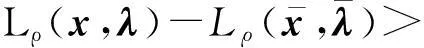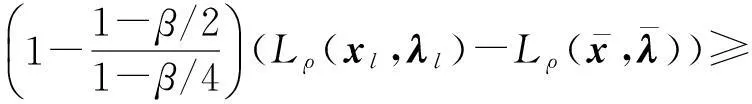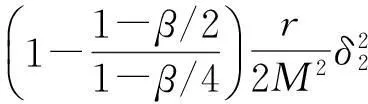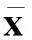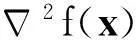一类不带二阶校正的超线性收敛滤子方法
刘美玲
(上海电机学院 数理教学部, 上海 201306)

一类不带二阶校正的超线性收敛滤子方法
刘美玲
(上海电机学院 数理教学部, 上海 201306)
摘要:提出了一类求解非线性约束优化问题的线搜索滤子算法。在滤子结构中用拉格朗日函数取代目标函数,在不用二阶校正的情况下可避免Maratos效应。在较弱的条件下,算法可得到全局收敛性和超线性收敛性。
关键词:非线性约束优化; 滤子; Maratos效应; 全局收敛; 超线性收敛

考虑以下的非线性约束优化问题:
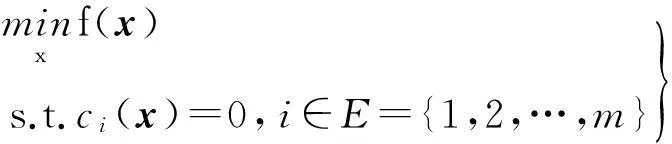
(1)
式中,x∈Rn,函数f∶Rn→R和ci(x)(i∈E)∶Rn→R假设为连续可微的。
相应的Lagrange函数为
L(x,λ)=f(x)+λTc(x)
(2)
式中,向量λ为Lagrange乘子;c(x)=(c1(x),c2(x),…,cm(x))。
Fletcher等在文献[1]中提出的滤子方法是求解问题(1)的最有效的方法之一。它的基本思想如下: 如果在一个试探点处能改善目标函数值或约束违反度函数值,则该试探点会被接受。
滤子方法可作为价值函数代替罚函数。因为罚参数一般是不易估计的。文献[1]中滤子方法的优良数值结果使得最近几年对它有了持续而深入的研究[2-10]。在这些研究中对全局收敛进行了广泛分析,但对超线性收敛性的研究较少,已有的主要成果有Ulbrich[3]提出的一类滤子SQP(Sequential Quadratic Programming)方法[3]和Wächter等[4]提出的一类带二阶校正步的线搜索滤子方法。文献[3]中的滤子方法在一个SQP信赖域框架下执行,但是为了获得超线性收敛性并尽量接收SQP完全步,其中的充分减少条件是比较复杂的,故在算法实际执行中比较耗时。而在文献[4-5]中的无二次子规划的线搜索方法中,滤子方法表现出了较好的稳定性,且基于线搜索技术的滤子方法不需要满足所有约束的线性化相容。但是,文献[4-5]中的线搜索滤子方法如果不用二阶校正步,则会受到Maratos效应影响,此时,滤子技术会阻止接收一个接近最优解的试探步,妨碍了局部收敛性,使得滤子不可接收一个完全的线搜索步,不能得到超线性收敛性。本文研究了一类不用二阶校正步的线搜索滤子算法,为了避免Maratos效应,用Lagrangian函数值代替滤子中的目标函数值,也能确保获得超线性收敛性。另外,该算法对充分减少条件的要求并不强,且算法可得到全局收敛性。
1算法机制
对一个给定的初始估计值x0,用一个线搜索算法产生一系列问题式(1)的最优解的较好估计xk,k为迭代次数,k∈N。式(1)的Karush-Kuhn-Tucker(KKT)条件为
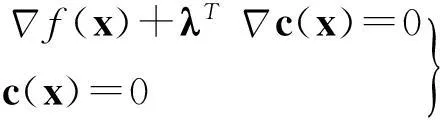
(3)

为了讨论简单,本文只考虑等式约束。通过设置松弛变量等方法,所提算法和收敛技术容易用到含不等式约束的问题中。在每一次迭代k,搜索方向dk通过计算xk处的KKT条件(式(3))的线性化,可得到
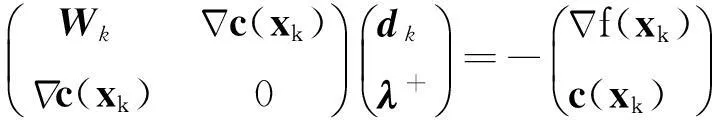
(4)
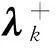
在得到一个搜索方向dk及一个步长αk∈[0,1]后,下一个试探步由
xk+1∶=xk+αkdk
得到。这里,用一个回溯线搜索程序获得一个步长值,主要是通过持续减少步长αk的值,直到某种接收准则被满足。本文的接收准则为滤子。
滤子方法的基本思想来自多目标优化中的支配概念[1]。
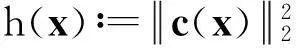
定义2一个滤子是指一列点对(hl,Ll),其中任何两个点对都不能互相支配。如果一个点对(hk,Lk)不被滤子中的任何一个点对支配,则其可被接收到滤子中。
当一个点对(hk,Lk)被接收到滤子中,也称迭代点xk被接收到滤子中。然而,单滤子条件不能充分保证得到全局收敛,故用一个强滤子条件(称为斜滤子[2])。因此,如果一个点xk相应的点对(hk,Lk)满足
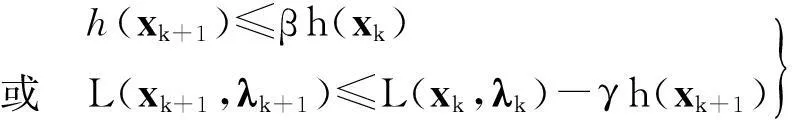
(5)
条件,则本文称该点可被滤子Fk接收。式中,定常数β,γ∈(0,1),实际算法执行时,通常设置β接近1,而γ接近0。
本文的接收准则给出了一个重要的包含性质,即如果一个点对(hk,Lk)被加到了滤子中,则新滤子的不可接受点集总是包含了旧滤子的不可接受点集[2]。
另外,设置函数L(xk,λk)的一个充分减少条件,与滤子条件结合作为试探步接受的充分减少条件: 记
ΔLk=L(xk,λk)-L(xk+1,λk+1)
作为函数L(xk,λk)的实际减少量,而
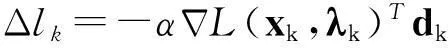
为L(xk,λk)的线性减少量;设函数L(xk,λk)的充分减少条件
ΔLk≥σΔlk,σ∈(0,1)
是一个前置参数。
在实际执行中,若线性系统(式(4))不相容,不能计算出搜索方向dk,故算法启动一个可行恢复项[4-5]。为了简单,本文假设线性系统总是相容的,故不考虑设置可行恢复项。本文给出下面算法步骤,用于求解问题式(1)。
(1) 给定初始点x0,常数β∈(0,1),γ∈(0,1),σ∈(0,1),τ∈(0,1),约束违反度函数h的上界hmax=max{104,1.2h(x0)}。
(2) 初始化。设α0=1,初始滤子F0={(hmax,L(x0,λ(x0)))},迭代数k=0。
(3) 对k=0,1,…,由式(4)计算搜索方向dk和 Lagrange乘子λk+1。当xk满足KKT条件(式(4))或dk=0时,算法停止;否则,算法进入下一步。
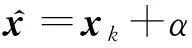
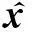
② 若Δlk>0和ΔLk<σΔlk成立,进入③;否则,增广滤子Fk+1=Fk∪{(h(xk+1),L(xk+1,λk+1))},进入步骤(5);
我无意中参与了一场巷战,被路过的老师扭送到校长室。校长看着我劣迹斑斑的违规记录,摆摆手说:“你回家去吧,以后,也不必再来了。”
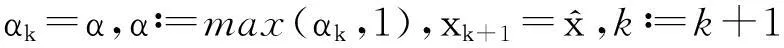
为方便陈述,若Δlk>0和ΔLk>σΔlk成立,则称xk为L-型迭代;若Δlk≤0,则迭代的主要目的是减少h,此时产生的迭代点称为h-迭代点。
注1为了防止hk→∞时一系列L-型迭代点被接收,给约束违反度函数h设置一个上界hmax。
2收敛分析
2.1 全局收敛
以下给出算法1的全局收敛分析。部分参考了文献[2,10]的证明思想。首先,给出假设条件:
A1所有的迭代点xk在Rn的一个非空闭有界集S中。
A2函数f、ci在S上二次连续可微。
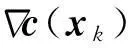
以上A1、A2是标准假设条件,A3、A4对获得收敛结果和确保算法可执行至关重要。
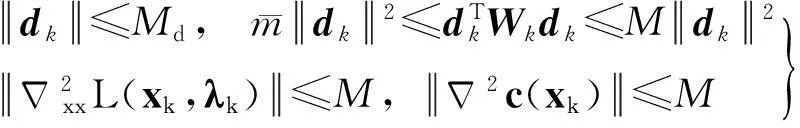
(6)
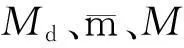
引理1假设Lk单调递减且下有界,对所有的k,如果
hk+1≤β hk或Lk-Lk+1≥γ hk+1
则hk→0。
证明如果hk+1≤βhk对所有充分大的k成立,则hk→0;否则在一个无穷迭代子序列上有Lk-Lk+1≥γhk+1成立。已知Lk单调减少且下有界,∑hk+1是有界的,因此,在该无穷子序列上有hk+1→0;但对于剩下的迭代点有hk+1≤βhk,因此在主序列上hk→0。
引理2设在无穷迭代序列{xki}处(h(xki),L(xki,λki))可被滤子接收,则
证明若引理结论不真,必存在一个无穷子序列{kj}⊂{ki},使得对所有的j和某个常数ε>0有
h(xkj)>ε
(7)
因此,在区域[hkj-(1-β)ε,hkj]×[Lkj-γε,Lkj]或该区域和V0∶=[0,hmax]×[Lmin,∞]的交集内没有其他的点对(h,L)会被加到滤子中,其中,Lmin≤L(xk,λk)是一个常数。易知这些区域的面积为(1-β)γε2,故集合V0∪{(h,L)|L≤cL}可被至多有限个这样的区域有限覆盖,其中,cL为常数并满足cL≥Lmin。
既然点对(hkj,Lkj)持续被加到滤子中,当i→∞,Lkj→∞,不失一般性,假设Lkj+1≥Lkj对所有充分大的j成立。但是,由式(5)和式(7),有
hkj+1≤β hkj
即得hkj→0,与式(7)矛盾。因此,假设Lkj+1≥Lkj错误,引理结论成立。
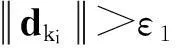
证明由线性系统式(4)及式(6),可得
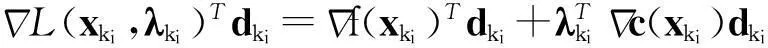
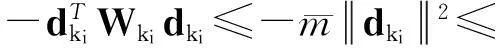
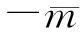
引理4设假设条件A1~A4成立,{xki}⊂{xk}是一个迭代点子序列,使得对独立于ki的常数ε2>0有
则必存在试探点可被滤子接收。
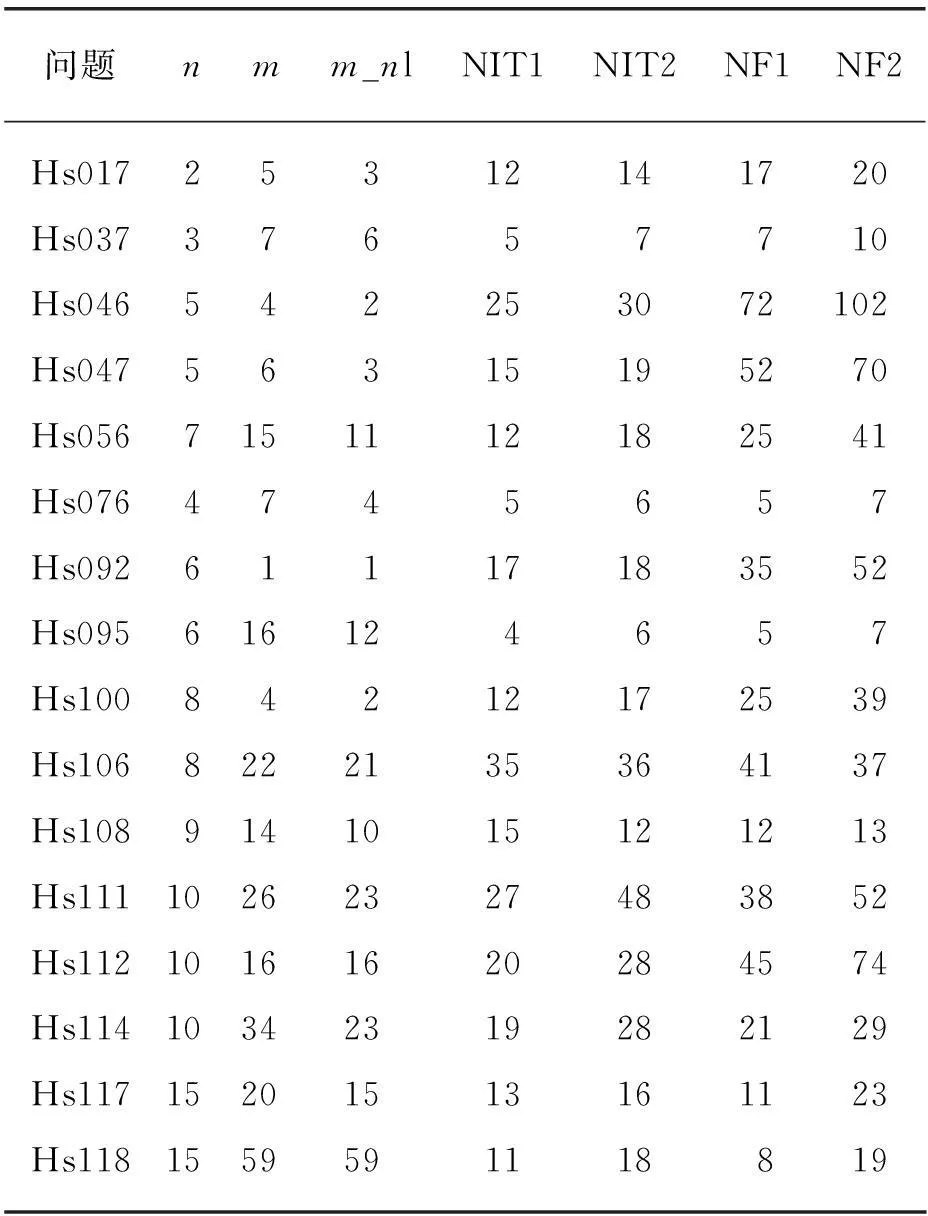
证明算法机制确保了第1个迭代点可被滤子接收。以下假设(h(xk),L(xk,λk))可被接收到第k个滤子中,且(h(xl),L(xl,λl))∈Fk,l 即 然后,由Taylor定理和式(6)可得 (8) 相似地,若 有 仍由Taylor定理,由式(4)、(6)可得 (9) 因此,再由式(8)、(9)得 L(xki+1,λki+1)≤L(xki,λki)≤L(xl,λl)-γh(xki) h(xki+1)≤h(xki)≤βh(xl) (10) 即引理结论为真。 定理1设假设条件A1~A4成立,且问题(1)有至少一个解。算法产生的迭代点序列{xk}必会有以下两种结果之一: (1) 问题(1)的一个KKT点找到。 (2) 存在一个聚点是一个KKT点。 证明只需要考虑结果(2)。以下分两种情况分析。 ΔLk=L(xk,λk)-L(xk+αdk,λ(xk+αdk))= (11) 此处用了引理3的结论,即 (2) 只有有限个h-型迭代点加到滤子中,则对所有的k≥K,xk是一个L-型迭代点,故 L(xk,λk) 严格单调减少。又因为 L(x,λ)=f(x)+λc(x) |ΔLki-Δlki|= (12) 另一方面,据引理3,有 即 (13) 由式(12)、(13)推得 (14) 以下进行局部收敛分析,证明在本文的滤子构造可避免Maratos效应,即一个试探步长αk=1可被接受。加一假设条件: (15) 在下文的证明中,定义 (16) 式中,ρ>0是一个常数。 (17) 由Taylor定理和 (18) 显然可得 (19) 其中,r是一个常数,参见文献[3]中的引理2。 (20) ∀d∈Rn 对所有的常数s>0,显然有 (21) (22) (23) 式中,常数t>0。则由式(22)、(23)可得引理结论。 引理6设假设条件A5成立,则对任何ζ∈[0,1]和M0≥1存在一个充分大的指标数K,使得对所有的k≥K,α=1及 (24) 点xj+1,j=k,k+1,…,可被滤子Fj∶=Fk∪(hk,Lk)∪(hk+1,Lk+1)∪…∪(hj,Lj)接受。 (25) 由引理5,得到 (26) 设 (27) 以下证明对K≤l≤k,xk可接收到(hl,Ll)∈Fk∪(hk,Lk),由式(24)得 再由式(26),可得 (28) 则由式(26)、(27)推出 (29) h(x)>β hl,L(x)+γh(x)>Ll 由此,可由式(25)、(26)得 (30) 由式(30)、(28)可推出 该结果与式(29)矛盾。因此,x可接收到滤子Fk∪(hk,Lk),即可推断(hj+1,Lj+1)可被接收到滤子Fl中。 定理2设假设条件A1~A5成立,则存在充分大的指标数K>0,使得对所有的k≥K,算法可接受αk=1的步,即 xk+1=xk+dk 证明定理结论可直接由引理6和注2得到。 3数值结果 本文给出算法1的一些数值计算结果,并且与三维滤子方法[12]进行比较。所有的数值计算问题均取自CUTE问题集。该问题集在NEOS网站可免费获取,算法程序由MATLAB7.0编写。参数设置如下: (1) 终止准则设置为 取ε=1×10-6,与文献[12]中取值相同。 (2) 取β=0.99,γ=10-4,σ=0.1。 数值试验参数如表1所示,表2给出了数值试验的结果;为了方便比较,表2中还给出了三维滤子线搜索算法的数值结果。 表1 试验参数说明Tab.1 Experimental parameters 表2 算例计算结果Tab.2 Numerical results 由表1可见,与三维滤子方法相比,算法1的数值结果显示了其具有较好的稳定性和有效性。 4结语 本文研究了一类求解非线性约束优化问题的线搜索滤子算法,将Lagrangian函数取代目标函数置于滤子中,可避免Maratos效应,设置一个辅助增广Lagrangian函数后,也可获得超线性收敛性。本文结果显示了线搜索滤子方法不用二阶校正步也可以得到较快的局部收敛速度。 参考文献: [1]Fletcher R,Leyffer S.Nonlinear programming without a penalty function[J].Mathematical Programming,2002,91(2): 239-269. [2]Fletcher R,Leyffer S,Toint P L.On the global convergenceof a filter-SQP algorithm[J].SIAM Journal on Optimization,2002,13(1): 44-59. [3]Ulbrich S.On the superlinear local convergence of a filter-SQP method[J].Mathematical Programming,2004,100(1): 217-245. [4]Wächter A,Biegler L T.Line search filter methods for nonlinear programming: Local convergence[J].SIAM Journal on Optimization,2005,16(1): 32-48. [5]Wächter A,Biegler L T.Line search filter methods for nonlinear programming: Motivation and global convergence[J].SIAM Journal on Optimization,2005,16(1): 1-31. [6]Gould N I M,Sainvitu C,Toint P L.A filter-trust-region method for unconstrained optimization [J].SIAM Journal on Optimization,2006,16(2): 341-357. [7]Nie Puyan.Sequential penalty quadratic programming filter methods for nonlinear programming [J].Nonlinear Analysis: Real World Applications,2007,8(1): 118-129. [8]Nie Puyan,Ma Changfeng.A trust region filter method for general nonlinear programming [J].Applied Mathematics and Computation,2006,172(2): 1000-1017. [9]Ulbrich M,Ulbrich S,Vicente L N.A globally convergent primal-dual interior-point filter method for nonconvex nonlinear programming[J]. Mathematical Programming,2004,100(2): 379-410. [10]Fletcher R,Gould N I M,Leyffer S,et al.Global convergence of a trust-region SQP-filter algorithm for general nonlinear programming[J].SIAM Journal on Optimization,2002,13(3): 635-659. [11]Nocedal J,Wright S J.Numerical Optimization(photoengraving)[M].Beijing: Science Press,China,2006: 45. [12]Shen Chungen,Xue wenjuan,Pu Dingguo.Global convergence of a tri-dimensional filter SQP algorithm based on the line search method[J].Applied Numerical Mathematics,2009,59(2): 235-250. 欢迎投稿《上海电机学院学报》 网址:http:∥shdj.cbpt.cnki.net 地址:上海市临港新城橄榄路1350号 上海电机学院文理楼205室 邮编: 201306 电话: (021)38223023(021)38223025 E-mail: shdjxb@163.com Superlinear Convergence Filter Method without Second Order Correction LIUMeiling (Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China) Abstract:A line search filter method for nonlinear constrained optimization is presented. Using the Lagrangian function value instead of the objective function value in the filter, the Maratos effect is avoided without an additional second order correction. Under some mild conditions, global convergence and superlinear convergence can be realized. Key words:nonlinear constrained optimization; filter; Maratos effect; global convergence; superlinear convergence 文献标志码:A 中图分类号:O 221.2 文章编号2095 - 0020(2015)01 -0034 - 08 作者简介:刘美玲(1981-),女,讲师,博士,主要研究方向为非线性规划,E-mail: liuml2004@163.com 基金项目:国家自然科学 资助(11371281);上海高校青年教师培养资助计划资助(ZZSDJ13008);上海电机学院二级基础学科建设项目资助(13XKJC01) 收稿日期:2015 - 01 - 10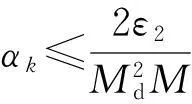
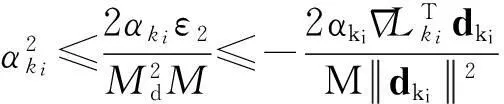
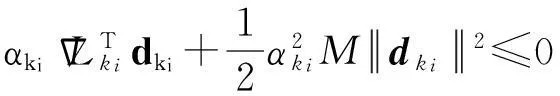
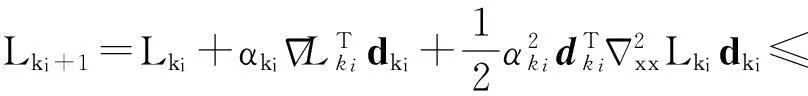
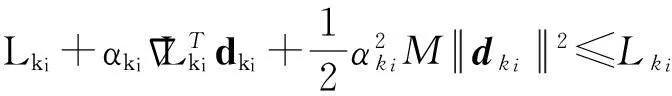
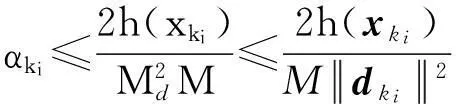
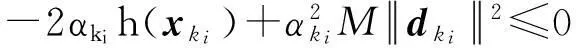
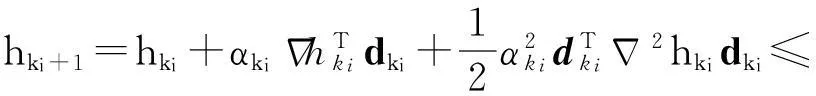
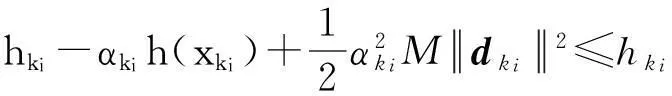
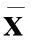
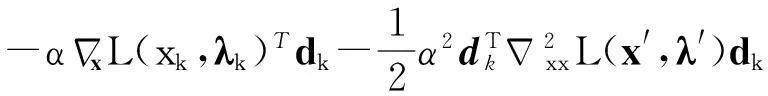
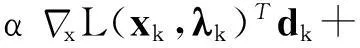
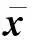
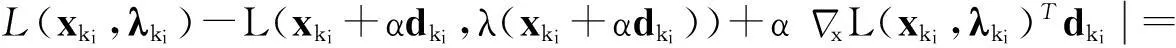
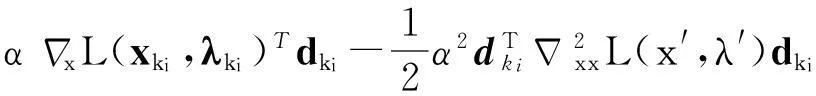
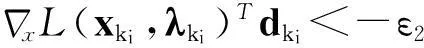
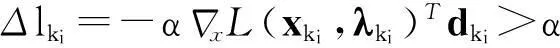
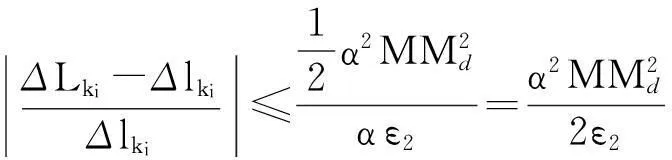
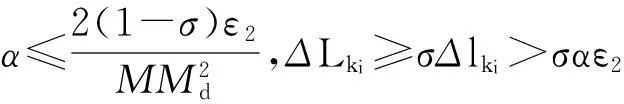
2.2 局部收敛