灰色预测技术研究进展综述
党耀国, 王俊杰, 康文芳
(南京航空航天大学 经济与管理学院, 南京 210016)

灰色预测技术研究进展综述
党耀国,王俊杰,康文芳
(南京航空航天大学 经济与管理学院, 南京 210016)
摘要:灰色预测技术是灰色系统理论的重要分支之一。分析了GM(1,1)模型的性质、GM(1,1) 模型的改进与优化、GM(1,1)模型参数估计、GM(1,1)模型初始条件优化、GM(1,1)模型的扩展与应用及幂模型的研究进展;最后对灰色预测模型的未来研究方向提出了建议。
关键词:灰色系统; GM(1,1)模型; 灰色预测; 优化

20世纪60年代,邓聚龙教授首先提出“去余控制”理论;随后其在1982年提出灰色控制理论。灰色系统理论是一种解决信息不完备系统的数学方法,以控制论的观点构建数学控制模型,用来分析样本小、信息不完全的不确定系统问题。目前,该理论已被国内外学者广泛关注。灰色系统理论通过30多年的发展,理论体系不断完善,分支结构越发清晰,实际应用面越来越宽泛,应用领域触及到了水文、能源、经济、管理、工程、交通等诸多方面。
灰色预测理论作为灰色系统理论的重要内容之一,同时也是一个新的现代预测方法。灰色预测方法在解决数据获取性较差的问题时,以少量可获取的信息为基础,利用灰色算子提高序列的光滑度、准指数性,生成新序列,进而实现预测,提高了预测的精度,有效解决了经济社会系统中数据缺失、不真实等影响研究工作的瓶颈问题,弥补了大样本建模要求的不足。
随着灰色预测方法的不断拓展,它越来越受到国内外学者的广泛认可。近期,在常用的中英文数据库中以“grey forecasting”和“灰色预测”为关键词进行搜索,共有13433篇中英文文献被检索到,其涉足领域包括了教育、能源、经济、环境、交通等多个领域(见表1)。
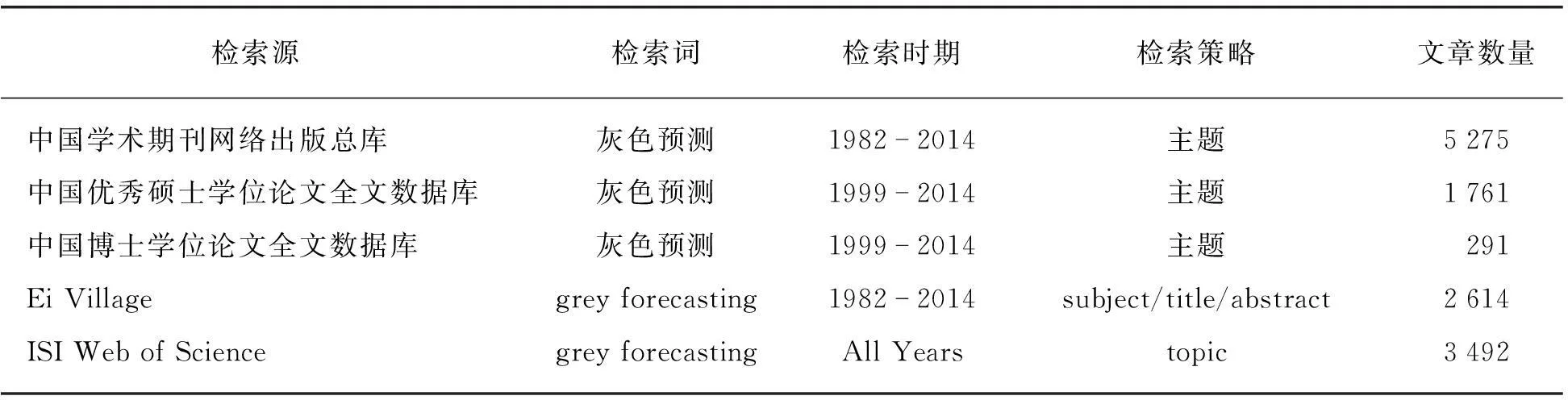
表1 灰预测论文常用数据库收录情况Tab.1 Search results of gray prediction papers from common databases
注:检索时间为2015年1月20日
对检索到的灰色预测论文进行分析,发现有关灰色预测方法的应用文献占到了绝大多数,而对灰色预测理论方法研究的文献相对较少。本文通过对灰色预测模型的研究,从GM(1,1)模型的性质研究、灰色微分方程的改进、参数估计方法的优化、初始条件的选择优化和GM(1,1)模型的扩展与应用研究以及GM(1,1)的幂模型研究三方面综述灰色预测模型的研究进展。
1灰色预测模型的研究进展综述
1.1 GM(1,1)模型研究进展
GM(1,1)模型既是灰色系统理论的重要组成部分,也是灰色预测理论的基础模型和核心模型。对于灰色预测模型的理论研究也主要集中在 GM(1,1) 模型的优化与拓展方面。1985年,邓聚龙教授[1]首先提出了GM(1,1)模型,并对其建模条件进行研究,提出了光滑比和级比检验等先验检验方法,求解了GM(1,1)模型的参数包,并提出多种扩展形式。此后,诸多国内外学者加入到灰色预测模型的理论研究中,并从模型性质、改进和应用等方面改进了GM(1,1)模型。
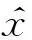
(2) 若序列x(0)(k)单调递增,则a<0;若序列x(0)(k)单调递减,则a>0;
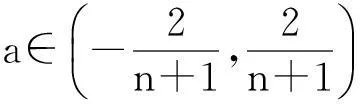
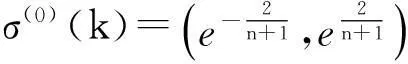
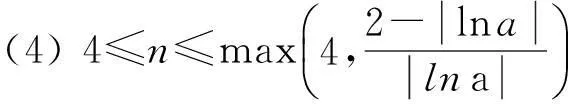
吉培荣等[3]以白指数序列为研究对象,通过分析GM(1,1)预测白指数序列的模拟误差,给出了无偏GM(1,1)模型。无偏GM(1,1)预测白指数规律的序列不存在预测和模拟误差。
王文平等[4]对带有非线性项的GM(1,1)和无偏GM(1,1)模型的混合特征进行研究;王正新等[5]在此基础上,通过研究其混合特性,合理阐述了GM(1,1)和无偏GM(1,1)的禁区现象:
(1) 在GM(1,1)模型中,发展系数为-1.2 (2) 在GM(1,1)模型中,发展系数为-1 (3) 在GM(1,1)模型中,当发展系数a<-1.124 时,原始GM(1,1)模型进入混沌区;无偏模型中,当发展系数a<-1.272538 时,无偏GM(1,1) 模型进入混沌区。由此可见,无偏GM(1,1) 模型的混沌区域比原始GM(1,1)模型缩小了。 郑照宁等[6]通过对GM(1,1)模型性质的研究,指出灰色预测模型全都存在严重的病态性,而且模型的病态性问题源自模型自身,并以此否定了灰预测模型的理论与应用价值。党耀国等[7]从矩阵的角度,利用矩阵条件对灰色预测模型的病态性问题进行研究,否定了灰色模型都存在病态性的结论,指出只有在常数序列中,并且除去首项、其余项都接近零的情况下,GM(1,1)模型才会出现此类病态问题。因此,GM(1,1)不存在严重的病态问题。李希灿等[8]提出了GM(1,1,β)模型的拓展形式: 参数包形式和内涵型,并对这两类拓展模型的性质进行研究,进而提出优化算法;研究结果表明,GM(1,1,β)灰微分方程模型参数a的客观取值范围是(-∞,+∞),经典模型则为(-2,+2);发展系数a的客观取值范围是由背景值系数β决定的,与原始数据无关。灰微分方程模型完全适合齐次指数数列。 1.1.2GM(1,1)灰色微分方程的优化与改进众多学者对GM(1,1)模型的灰导数进行了改进研究。目前灰导数的改进思路大致分为向后差商和向前差商后进行加权平均。张彤等[9]利用梯形面积和中点公式的求解思路,对GM(1,1)的灰导数进行推导,改进了灰导数的求解方法,提高了模型预测精度。王义闹等[10]首先对原始序列进行向后差商和向前差商,然后求解加权平均值,并以此作为GM(1,1)灰导数的白化公式,求解灰导数;得出该模型通过线性变化后,预测结果不变的性质,同时模拟和预测精度也得到提高。在此基础上,文献[11]中提出逐步求解灰导数,动态优化GM(1,1)模型的灰导数,不仅提高了灰预测模型的精度,更解决了发展系数a绝对值过大时无法进行预测的问题。穆勇[12]对GM(1,1)灰导数的白化值求解方法进行改进,使得GM(1,1)模型具有无偏性,并且给出了无偏GM(1,1)模型有白指数重合性的证明。李玻等[13]通过研究文献[10]中灰导数的白化方法,给出了其白化方法的合理性,进而改进了加权系数的确定方法,给出了表达式,提高了预测模型的精度。张凌霜等[14]对非等间距的时间序列进行研究,并改进了非等间距序列的背景值求解方法,利用逐步递推的思想对背景值求解中的加权系数进一步优化。 GM(1,1)的背景值z(1)(k)是通过一次累加后均值生成的,背景值的生成过程是否准确将直接影响模型的预测精度,因为背景值对GM(1,1)模型的参数包求解造成直接影响,发展系数a和灰作用量b都依赖于背景值,而GM(1,1)的时间响应函数的准确度取决于a和b。背景值构造的偏差与数据变化趋势相关度较大,时间序列数据变化趋势平缓时,背景值精确度较高,反之偏差较大。因此,许多学者都对背景值的优化进行了探讨。其中,谭冠军[15]第一个提出GM(1,1)模型的背景值优化,并从z(1)(k)的几何意义入手定义了一个全新的背景值求解公式: (m-1)x(1)(k+1)] m=2,3,…,n 其他一些学者将背景值推广为 z(1)(k)=αx(1)(k-1)+(1-α)x(1)(k) 其中,α∈(0,1)为待求参数。从以上公式可以看出确定公式中的参数α是求解背景值的关键。向跃霖[16]采用黄金分割法对α值进行搜索,并以模拟误差的平方和最小为搜索目标,进而求解参数α。谢开贵等[17]提出利用遗传算法来确定参数α,因为目标函数不一定可微,而且α与模拟误差之间是非线性关系。王义闹等[18]通过探讨发展系数a与背景值公式中的参数α之间的联系,得出结论如下: (3)α(a)是严格的单调递减函数。 罗党等[19]从另一个角度改进了背景值的公式,利用齐次指数函数对一次累加生成序列进行拟合,进而构造了新的背景值公式,提高了预测精度。Lin等[20]结合残差傅里叶变换思路,根据灰预测的时间响应函数,构造了一种新型的背景值公式,改进了GM(1,1)模型。王正新等[21]认为经过一次累加后,离散的齐次指数函数将变为离散的非齐次指数函数;反之离散的非齐次指数函数经过一次累减后将变为离散的非齐次指数函数,并给出了证明,在此基础上改进了背景值。 1.1.3GM(1,1)模型参数估计方法穆勇[22]认为,由于线性规划中折扣系数是依靠经验得来,从而导致了参数确定偏差,故提出采用折扣最小二乘法对GM(1,1)进行参数估计,并求解出了折扣最小二乘法的小生境遗传算法,削弱了参数的偏差问题。肖新平等[23]采用模拟误差平方和最小化的准则,对GM(1,1)模型的参数估算方法进行优化,通过探讨原始序列的平移变换对参数确定的作用给出了参数优化方法。何文章等[24]从3种不同的差商方式出发上,提出了GM(1,1)参数的线性规划优化方法。Wang等[25]为了提高预测精度,利用遗传算法对GM(1,1)的参数进行估计,效果良好。张岐山[26]将微粒群算法引入GM(1,1)模型参数估计中,对背景值求解公式中的参数α和边值进行优化,提高了灰色预测的精度。Hsu等[27]的研究对象为电力需求,属于长期预测,其将小样本参数估计的统计方法引入到GM(1,1)的参数估计中,拓宽了灰预测方法的适应范围,使其能应用于中长期预测。Shih等[28]引入遗忘因子的概念和递推的思想,对具有时变参数的 GM(1,1) 模型运用递推最小二乘法进行估计,提高了预测精度。王义闹等[29]针对灰预测模型检验与模型优化脱节的问题,基于平均相对误差最小化的原则,提出了一类估计指数型参数估计方法,从理论上最小化了预测模型的平均相对误差绝对值。 1.1.4GM(1,1)模型初始条件的优化经典GM(1,1)模型是以序列中第一个数据为白化微分方程的初始条件进行求解的,邓聚龙[30]考虑到灰色系统理论中的新信息优先原理,并同时证明了序列第一个数据与模型的预测值和发展系数并无关系。随后,许多研究学者对GM(1,1)模型的初始条件进行深入研究。党耀国等[31]提出以时间序列中最新的一个数据作为模型求解的初始条件,是对灰色系统新信息优先原理的重要体现;此外,基于样本综合最优化原理,可选取最小偏差中间数据为初始条件,以及原始累加序列与模拟累加序列偏差平方和最小和平均相对偏差最小、原始序列与模拟序列偏差平方和最小等方法。王育红等[32]从线性组合的角度,以首个数据和最后一个数据作线性组合作为初始条件,并用最优化思想求解权重系数。 1.1.5GM(1,1)模型扩展及其应用研究邓聚龙[33]提出了GM(1,1)模型群,在GM(1,1)模型的基础上,从定义和白化过程出发,推导出了 GM(1,1,x(1))、GM(1,1,x(0))、GM(1,1,b)、GM(1,1,exp) 和GM(1,1,C)5种派生模型。宋中民等[34]通过深入研究建模机理提出了中心逼近式的灰色GM(1,1)模型。Chen等[35]为了进一步体现GM(1,1)模型的动态性,结合时间序列ARMA的建模机理,提出了 DGDM(1,1,1) 模型,并得到广泛应用。Hsu等[36]应用人工神经网络修正GM(1,1)模型的残差,取得了较好的预测效果。谢乃明等[37]构建了离散GM(1,1)模型,并给出了递推求解算法,通过研究该模型的性质,发现离散GM(1,1)模型对于白指数序列建模具有完全重合性。姚天祥等[38]在离散GM(1,1)模型的基础上,对其建模的初始条件进行深入研究。Wang等[39]研究了离散GM(1,1)模型的无偏性,并给出了递推解法,同时求解了不同初始条件下无偏模型的对推公式,对两种不同准则下的初始条件进行了优化。王正新等[40]提出利用时间系数修正等间距时序,解决了GM(1,1)模型无法应用在大波动序列的问题;同时,给出了时间权重系数的计算方法,利用反向累加生成算子,建立GOM(1,1)模型,结合GM(1,1)和GOM(1,1)模型,提出两阶段灰色预测模型。钱吴永等[41]引入序列转换法则,对振荡序列利用转换法则转化为单调序列,再利用灰色预测模型有效地解决了振荡序列预测问题。 实际问题中存在着大量的非等间距时序问题,而经典的GM(1,1)模型仅适用于等间距序列的预测和模拟。因此,许多学者对非等间距序列的预测问题展开研究。罗佑新等[42]通过研究给出了直接建模法的前提条件: 初始序列需具备单调性、非负性、上凹性等性质,并且需要满足 [max Δtk/min Δtk]<2 Shi[43]首先利用线性变化负责将非等间距序列转化为等间距序列,然后通过逆变换还原。史雪荣等[44]运用上述文献的序列生成方法,分析了变参数非等间距 GM(1,1) 模型及应用。蒋卫东等[45]避免了对原始非等间距序列的人为改造,提出时数分离法,通过概念的转换得到两个等间距序列,但对于这类转换需进一步研究其同步预测性。戴文战等[46]借用文献[19]中所提出的背景值优化模型,构建了非等间距GM(1,1)模型,提高了建模的精度。王叶梅等[47]则利用文献[40]中提出的背景值最优模型,构建了新的非等间距模型,得到了较高的模拟精度。但是,对于非等间距序列的建模条件、生成方法等研究较少,目前较多的是对非等间距灰预测模型的简单推广,建模机理、生成原则和转换前提等有待进一步深入研究。肖新平等[48]对广义累加灰色预测控制模型进行了深入分析,得出该灰预测模型其实是跳跃模型、非等间距模型和阶段模型的统一变现形势,并且对初始点的变化对模型参数及预测值的影响进行了研究,利用矩阵分析推导了它们之间的数量关系;利用广义累加生成矩阵,对其中的元素、初始点和初始条件选取进行优化,并对广义累加灰色预测控制模型进行组合优化。郭晓君等[49]以含时间幂次项的灰色模型为基础GM(1,1,tα),构建了灰色 GM(1,1,tα) 与自忆性原理的耦合预测模型;用动力系统自忆性原理来克服传统灰色模型对初值比较敏感的弱点。 GM(1,1)幂模型是灰色预测模型的拓展,是GM(1,1)模型和Verhulst模型的推广,对具有单峰特征的数据具有较好的模拟效果。幂模型中的灰作用量的幂指数可以灵活调整,以拟合不同特征曲线,这是该模型的最大特点。王正新等[50]提出了幂指数的白化公式,结合灰色系统的信息覆盖思想,给出了幂模型的求解方法,并分析了幂指数的变化对模型求解的影响。当幂指数取2时,即为灰色Verhulst模型。 事物在开始阶段增长缓慢,随后增速逐步增大,然后进入高速增长期,最后进入低速增长期直至停止增长,因此,事物的发展过程一般呈S形态,灰色Verhulst模型即适用于此类形状。该模型首先对原始序列进行一阶累加生成,然后建立灰色预测模型;相比于传统Verhulst模型,其把序列近似为单峰型数据,拓宽了传统Verhulst模型应用宽度,提高模拟精度。若原始数据本身即是S形态,且为小样本数据,则可直接建立灰色Verhulst模型。何文章等[51]对灰色Verhulst模型的参数估计方法和初始条件进行优化,提高了模拟预测的效果。Wang等[52]从梯形面积公式的白化灰导数出发,提出了一种新的灰色 Verhulst 定义式,提高了差分方程参数与微分方程中参数的一致性。Kayacan等[53]引入傅里叶变换,对灰色Verhulst的模拟误差进行修正,提高模拟效果,并用改进的模型对欧元对美元的汇率走势进行预测。王正新等[54]利用非齐次指数函数的倒数生成算子,构建了无偏灰色Verhulst模型,降低了模型本身存在的固定偏差。杨德岭等[55]对“灰度不减”公理进行延伸,得到了“信息域不减”的推论;然后,构建核序列的Verhulst模型,并以信息域不减推论为依据、以核为中心推导区间灰数上(下)界的时间响应式。王正新[56]对原始序列建立 GM(1,1) 幂模型以描述系统行为的总体趋势;然后,利用傅里叶级数提取模型的残差序列所包含的周期性振荡规律,并以两者之和构成新的时间响应函数;最后以平均误差最小化为目标,建立非线性优化模型求解最优参数。王正新[57]提出一种时变参数GM(1,1)幂模型,通过引入多项式函数描述GM(1,1)幂模型的结构参数随时间的动态变化规律;根据建模样本量的不同,分3种情形给出了模型的参数辨识算式,同时给出了时变参数GM(1,1)幂模型白化方程的解析解,利用积分复合梯形公式将其转化为可用于预测的离散时间响应式,并提出了参数优化方法。 2灰色预测模型研究展望 目前,对灰色预测模型的研究主要集中在 GM(1,1) 模型的优化与拓展,提高GM(1,1)模型的预测精度。对于拓广灰色预测模型适用范围的研究较少。在工业、农业、经济、管理等实际应用领域中,周期型数据、时滞型数据、变趋势型数据、多因素截面数据、多因素面板数据、灾变数据、振荡型数据等不同特征的数据普遍存在。对于不同类型的数据,构建对应的GM(1,1|T)、GM(1,n,τ(i))、GM(1,n,T(i))、GDM(1,n|τ,κ)适用模型,同时,探究各类模型的性质,分析模型的适用范围和参数的求解方法。 随着社会经济、科学、技术等各方面的不断发展,人们所面临的实际问题越来越复杂,数据量越来越大,如何有效地从大数据中提取有效信息是对问题未来发展趋势准确预测的前提。因此,对灰色组合预测模型的研究具有一定必要性。如利用灰关联、灰决策模型对多因素预测问题需要先对因素进行筛选,增强预测的有效性;灰色预测模型与博弈模型、控制模型、投入产出模型等组合运用,将有效地处理复杂预测决策问题。 参考文献: [1]Deng Julong.The Control problems of grey systems[J].Systems & Control Letter,1982(5): 288-294. [2]刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践,2000,20(5): 121-124. [3]吉培荣,黄巍松,胡翔勇.无偏灰色预测模型[J].系统工程与电子技术,2000(6): 6-7,80. [4]王文平,邓聚龙.灰色系统中GM(1,1)模型的混沌特性研究[J].系统工程,1997,15(2): 13-16. [5]王正新,党耀国,刘思峰.无偏GM(1,1)模型的混沌特性分析[J].系统工程理论与实践,2007,27(11): 153-158. [6]郑照宁,武玉英,包涵龄.GM模型的病态性问题[J].中国管理科学,2001(5): 38-44. [7]党耀国,王正新,刘思峰.GM(1,1,β)灰色模型的病态问题研究[J].系统工程理论与实践,2008,28(1): 156-160. [8]李希灿,袁征,张广波,等.GM(1,1,β)灰微分方程的若干性质[J].系统工程理论与实践,2014,34(5): 1249-1255. [9]张彤,王子才,吴建伟.GM(1,1)模型参数的改进计算方法[J].系统工程与电子技术,1998,20(8): 58-60. [10]王义闹,刘开第,李应川.优化灰导数白化值的GM(1,1)建模法[J].系统工程理论与实践,2001,21(5): 124-128. [11]Wang Y N,Chen Z J,Gao Z Q,et al.A generalization of the GM(1,1) direct modeling method with a step by step optimizing grey derivative’s whiten values and its applications[J].Kybernetes,2004,33(2): 382-389. [12]穆勇.优化灰导数白化值的无偏灰色GM(1,1)模型[J].数学的实践与认识,2003,33(3): 13-16. [13]李玻,魏勇.优化灰导数后的新GM(1,1)模型[J].系统工程理论与实践,2009,29(2): 100-105. [14]张凌霜,王丰效.逐步优化灰导数的非等间距GM(1,1)模型[J].数学的实践与认识,2010,40(11): 63-67. [15]谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践,2000,20(4): 98-103. [16]向跃霖.废气排放量灰色建模新法初探[J].环境科学研究,1995,8(6): 45-48. [17]谢开贵,李春燕,周家启.基于遗传算法的GM(1,1,λ)模型[J].系统工程学报,2000,15(2): 168-172. [18]王义闹,刘光珍,刘开第.GM(1,1)模型的一种逐步优化直接建模方法[J].系统工程理论与实践,2000,20(9): 99-104. [19]罗党,刘思峰,党耀国.灰色模型GM(1,1)优化[J].中国工程科学,2003,5(8): 50-53. [20]Lin Y H,Lee P C.Novel high-precision grey forecasting model[J].Automation in Construction,2007(16): 771-777. [21]王正新,党耀国,刘思峰.基于离散指数函数优化的GM(1,1)模型[J].系统工程理论与实践,2008,28(2): 61-67. [22]穆勇.灰色预测模型参数估计的优化方法[J].青岛大学学报(自然科学版),2003,16(3): 95-98. [23]肖新平,宋中民,李峰.灰技术基础及其应用[M].北京: 科学出版社,2005: 102-123. [24]何文章,宋国乡,吴爱弟.估计GM(1,1)模型中参数的一族算法[J].系统工程理论与实践,2005,25(1): 69-75. [25]Wang Chaohung,Hsu L C.Using genetic algorithms grey theory to forecast high technology industrial output[J].Applied Mathematics and Computation,2008(195): 256-263. [26]张岐山.提高灰色GM(1,1)模型精度的微粒群方法[J].中国管理科学,2007,15(5): 126-129. [27]Hsu C C,Chen C Y.Applications of improved grey prediction model for power demand forecasting[J].Energy Conversion and Management,2003,44(14): 2241-2249. [28]Shih N Y,Shih N J,Yu W C.The parameter estimation of time-varying GM(1,1)[J].Journal of Grey System,2006,9(1): 51-56. [29]王义闹,吴利丰.基于平均相对误差绝对值最小的GM(1,1)建模[J].华中科技大学学报(自然科学版),2009,37(10): 29-31. [30]邓聚龙.累加生成灰指数律: 灰色控制系统的优化信息处理问题[J].华中工学院学报,1987,15(5): 7-12. [31]Dang Yaoguo,Liu Sifeng,Chen Kejia.The GM models thatx(n) be taken as initial value[J].Kybernetes,2004,33(2): 247-254. [32]Wang Yuhong,Dang Yaoguo,Li Yueqing,et al.An approach to increase prediction precision of GM(1,1) model based on optimization of the initial condition[J].Expert Systems with Applications,2010,37(8): 5640-5644. [33]邓聚龙.五种灰色预测[J].模糊数学,1985,5(2): 33-42. [34]宋中民,同小军,肖新平.中心逼近式灰色GM(1,1)模型[J].系统工程理论与实践,2001,21(5): 110-113. [35]Chen C K,Tien T L.The indirect measurement of tensile strength by the deterministic grey dynamic model DGDM(1,1,1)[J].International Journal of Systems Science,1997,28(7): 683-690. [36]Hsu C C,Chen C Y.A modified grey forecasting model for long-term prediction[J].Journal of The Chinese Institute of Engineers,2003,26(3): 301-308. [37]谢乃明,刘思峰.离散GM(1,1)模型与灰色预测模型建模机理[J].系统工程理论与实践,2005,25(1):93-99. [38]姚天祥,刘思峰,党耀国.初始值优化的离散灰色预测模型[J].系统工程与电子技术,2009,31(10):2394-2398. [39]Wang Z X,Dang Y G,Liu B.Recursive solution and approximating optimization to grey models with high precision[J].Journal of Grey System,2009,21(2): 185-194. [40]王正新,党耀国,刘思峰.两阶段灰色模型及其应用[J].系统工程理论与实践,2008,28(11): 109-114,121. [41]钱吴永,党耀国.基于振荡序列的GM(1,1)模型[J].系统工程理论与实践2009,29(3): 149-154. [42]罗佑新,周继荣.非等间距GM(1,1)模型及其在疲劳试验数据处理和疲劳试验在线监测中的应用[J].机械强度,1996,18(3):60-63. [43]Shi B Z.Modeling of the non-equigap GM(1,1) modeling[J].The Journal of Grey System,1993,5(2): 105-114. [44]史雪荣,王作雷,张正娣.变参数非等间距GM(1,1)模型及应用[J].数学的实践与认识,2006,36(6): 216-220. [45]蒋卫东,李夕兵,赵国彦.非等时序列预测的时数分离研究[J].系统工程理论与实践,2003,23(1): 68-72. [46]戴文战,李俊峰.非等间距GM(1,1)模型建模研究[J].系统工程理论与实践,2005,9(9): 89-93. [47]王叶梅,党耀国,王正新.非等间距GM(1,1)模型背景值的优化[J].中国管理科学,2008,16(4): 159-162. [48]肖新平,刘军,郭欢.广义累加灰色预测控制模型的性质及优化[J].系统工程理论与实践,2014,34(6): 1547-1556. [49]郭晓君,刘思峰,方志耕,等.灰色GM(1,1,tα)模型与自忆性原理的耦合及应用[J].控制与决策,2014,29(8): 1447-1452. [50]王正新,党耀国,刘思峰,等.GM(1,1)幂模型求解方法及其解的性质[J].系统工程与电子技术,2009,31(10): 2380-2383. [51]何文章,吴爱弟.估计Verhulst模型中参数的线性规划方法及应用[J].系统工程理论与实践,2006,26(8): 141-144. [52]Wang Zhengxin,Dang Yaoguo,Wang Yemei.A new grey Verhulst model and its application[C]∥Proceedings of the 2007 IEEE International Conference on Grey Systems and Intelligent Services.[S.L.]: IEEE,2007: 571-574. [53]Kayacan E,Ulutas B,Kaynak O.Grey system theory-based models in time series prediction[J].Expert Systems with Applications,2010,37(2): 1784-1789. [54]王正新,党耀国,刘思峰.无偏灰色Verhulst模型及其应用[J].控制与决策,系统工程理论与实践,2009,29(10): 138-144. [55]杨德岭,刘思峰,曾波.基于核和信息域的区间灰数Verhulst模型[J].控制与决策,2013,28(2): 264-268. [56]王正新.基于傅立叶级数的小样本振荡序列灰色预测方法[J].控制与决策,2014,29(2): 270-274. [57]王正新.时变参数GM(1,1)幂模型及其应用[J].控制与决策,2014,29(10): 1828-1832. Survey of Gray Prediction Model Research DANGYaoguo,WANGJunjie,KANGWenfang (College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China) Abstract:Gray prediction is an important branch of the gray system theory. Six aspects were summarized for the existing research of gray prediction. These are the property research of GM(1,1) model, improvement and optimization of GM(1,1) model, parameter estimation method, optimization of initial condition, extension and application researches of GM(1,1) model, and research on power model. Finally, two suggestions are made for the future study of gray prediction models. Key words:gray system; GM(1,1) model; gray prediction; optimization 文献标志码:A 中图分类号:N 941.5 文章编号2095 - 0020(2015)01 -0001 - 07 作者简介:党耀国(1964-),男,教授,博士生导师,主要研究方向为灰色系统理论,E-mail: iamdangyg@163.com 基金项目:国家自然科学 资助(71071077,71371098);中央高校基本科研业务费专项资金资助(NC2012001);江苏省高校哲学社会科学重点研究基地重大项目资助(2012JDXM005) 收稿日期:2015 - 01 - 15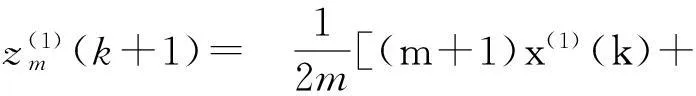
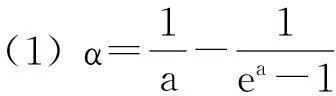
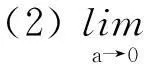
1.2 GM(1,1)幂模型研究进展

