基于能量法的材料弹塑性能力分析

孙　渊

(上海电机学院 机械学院, 上海 200245)



基于能量法的材料弹塑性能力分析

孙渊

(上海电机学院 机械学院, 上海 200245)

摘要:通过纳米压痕测试法探讨了碳纤维的弹塑性变形行为，得到了在0.5mN和2.5mN下的非线性载荷与位移曲线、最大压入深度hmax、压痕接触深度hc以及残留压痕深度hf，并计算了碳纤维的弹性回弹能力ζ和塑性变形能Eelastic。实验结果表明，碳纤维的弹性回弹量e随着载荷的增加而增加，但回弹能力ζ将随着载荷的增加而逐渐下降；塑性变形能Eelastic随着载荷的增加而增加，即材料的储存能量的能力随着载荷的增加而增加，而弹性能量恢复率η随着载荷的增加而减少，即材料释放能量的能力随着载荷的增加逐渐减少，对于碳纤维其弹性能量恢复率小于弹性回弹能力，即η<ζ。

关键词:载荷与位移曲线; 回弹能力; 塑性变形能

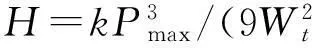
1能量计算原理

在加载过程中，被测试样在压头作用下开始发生弹性变形，随着载荷的增加，试样开始发生弹塑性变形，加载曲线呈非线性；卸载曲线反映了被测物体的弹性恢复过程，由于不可恢复的塑性变形，因此，在样品表面会产生微小的压痕形貌。通过压痕法所得到的载荷/位移曲线如图1所示，曲线的形状基于材料的弹塑性性能。通过分析载荷/位移曲线可以得到材料在最大载荷处Pmax下的最大压入深度hmax、压痕接触深度hc以及卸载后由于塑性变形而形成的残留压痕深度hf。

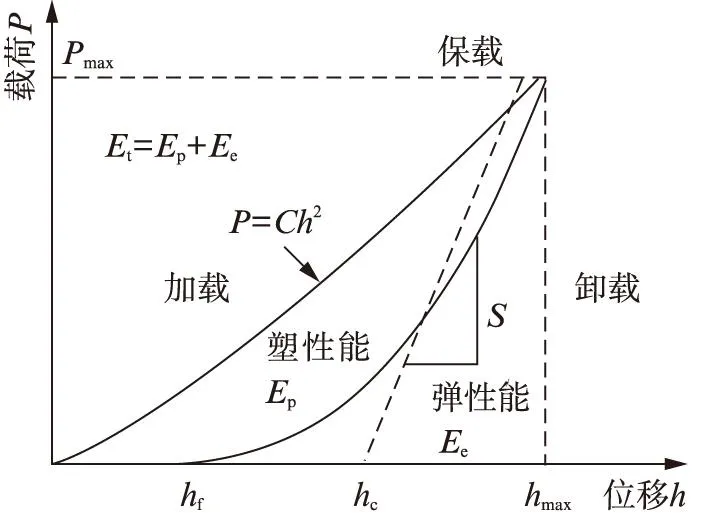
图1　典型的载荷/位移曲线Fig.1　Load-displacement curve

压痕接触深度hc可表示为卸载曲线顶部切线(接触刚度S=dP/dh)和横轴的交点。其值为

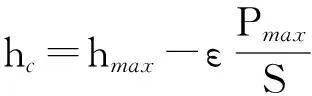
(1)

式中，ε是一个依赖于压头几何形状的常数，对Berkovich压头，ε=0.75。在加载过程中，材料将发生不同程度的弹塑性变形，由于载荷的作用，在这过程中所产生的总能量为

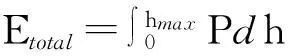
卸载后，由于材料的弹性回弹和能量释放，将产生一定的回弹量,

e=hmax-hf

弹性回弹能力可表示为

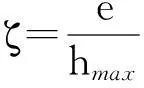
(2)

同样，通过卸载曲线可以描述弹性回复能为

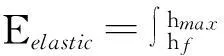
弹性能量回复率η可用弹性能与总能量之比描述，即

η=Eelastic/Etotal

(3)

因此，在压入过程中材料发生弹塑性变形产生塑性流动，形成不可恢复的塑性位移而做的塑性能为

Eplastic=Etotal-Eelastic=

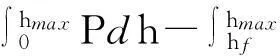
(4)

塑性能反映了材料储存能量的能力，在加卸载过程中，载荷P与压入深度h之间的关系为

P=C hm

式中,对于Berkovich压头，m=2，C由材料的接触性能决定[15]。当发生弹塑性行为时，

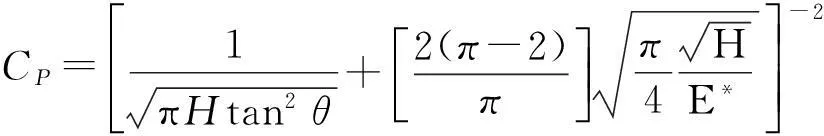
其值与材料的硬度H和接触弹性模量E*有关；当在卸载过程中，

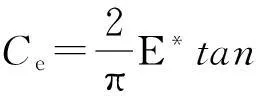
其值与材料的E*有关，θ为压头的角度。在最大载荷处，

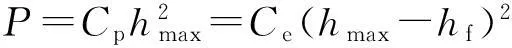
代入式(4)可得

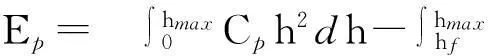
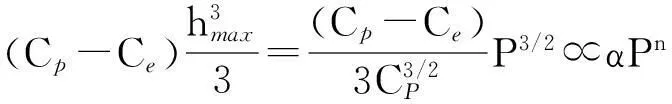
(5)

因此，塑性变形能可认为是载荷P的函数，α为系数。

2试样

试样材料为碳纤维，单丝的直径为6~7μm，为满足纳米压痕硬度的测量要求，材料经过打磨和抛光，获得了较为均匀的组织，通过光学显微镜可以看出其结构(见图2)，它由系列单丝和树脂基体组合在一起，并有一些裂纹，这与生产工艺有关。

图2　断面结构图Fig.2　Section structure

采用美国MTS公司生产的Nano Indenter Ⅱ纳米压痕仪，并结合Quesant公司的原子力显微镜进行图像观察和扫描。采用载荷模式加载，加载时间和卸载时间为10s，停留时间为1s,每一个载荷下重复进行压痕实验至少5次。通过压痕实验可以得到该材料的P-h曲线，在最大载荷Pmax下的压痕深度为hmax，卸载后由于弹性回复而残留压痕深度hf以及压痕接触深度hc，通过分析载荷和位移曲线，计算了材料的弹性回弹量e和回弹能力ζ，材料储存能量即塑性能Eelastic以及弹性能量恢复率η。

3结果与讨论

3.1　弹性回弹量和回弹能力

通过纳米压痕法，对碳纤维进行压痕实验，得到了相应的载荷/位移曲线,如图3所示，载荷施加范围从0.5mN开始到2.5mN，通过载荷/位移曲线，可以直观地描述载荷作用下的压痕行为，在最大载荷Pmax下的位移hmax，和卸载后即载荷为零时，由于塑性变形而形成的不可恢复的残留压痕深度hf，以及经过计算得到压痕接触深度hc。例如，在载荷为2.5mN时，其最大位移为345.1nm，压痕接触深度为 220.9nm，残留压痕深度为45.23357nm；而在载荷为0.5mN时，其最大位移为115.3nm,压痕接触深度为64.2nm，残留压痕深度为1.07087nm。因此,可通过e=hmax-hf来计算材料的弹性回弹量，并描述其弹性回弹能力ζ=e/hmax。图4描述了在载荷作用下材料的弹性回弹量e和回弹能力ζ。在加载过程中，其最大压入深度、压痕接触深度和残留压痕深度均随着载荷的增加而增加，由于材料的弹性回弹特性，其回弹量e也随着载荷的增加而增加，表现出强大的回弹能力。但随着载荷的增加，将发生较大的不可恢复的塑性变形，其回弹能力将随着载荷的增加而逐渐下降。例如在载荷为0.5mN时，其弹性回弹能力ζ高达98.5%，伴随较小的塑性变形；而在载荷为2.5mN时，其弹性回弹能力ζ下降为90.2%，产生较大的塑性变形，形成稍大的残留压痕深度。

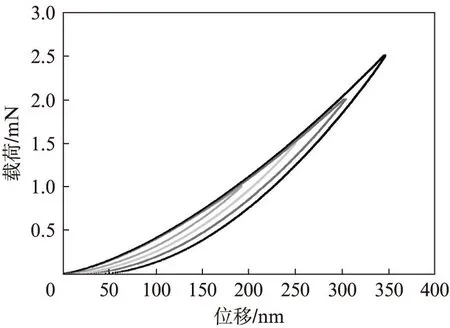
图3　载荷/位移曲线 Fig.3　Load-displacement curve

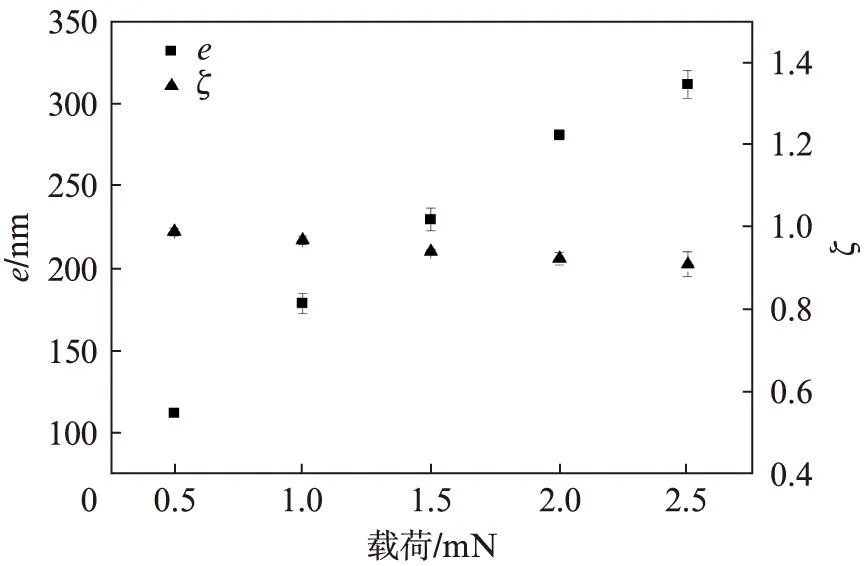
图4　弹性回弹量与回弹能力Fig.4　Ratio of elastic recovery and elastic recovery

3.2　塑性能和弹性能量恢复率

通过压痕法描述了材料在载荷作用下所产生的弹塑性变形，塑性变形是不可恢复，塑性变形能的大小可以描述材料储存能量的能力，弹性变形能可以描述材料释放能量的能力，弹性回弹能力ζ大，其弹性能量恢复率η也高。这里主要探讨碳纤维的塑性变形能和弹性能量恢复率η(见图5)，塑性变形能随着载荷的增加而增加，即材料的储存能力随着载荷的增加而增加，根据实验数据进行了非线性拟合，得到函数关系Ep=0.02744P1.79，即塑性能量是载荷P的1.79次方，式(5)中描述了材料的塑性能量在理论上应是载荷P的1.5次方，实验数据的拟合公式中n=1.79与理论公式n=1.5存在了一定的误差，但是可以通过系数α修正，因此实验结果与理论具有较好的吻合。碳纤维的弹性能量恢复率η随着载荷的增加而减少，即释放能量的能力逐渐减少，例如在载荷为0.5mN时，材料储存能量的能力较小，其弹性能量恢复率高达88.01%，释放能量的能力较大；而在载荷为2.5mN时，材料储存能量的能力较大，其弹性能量恢复率下降为79.28%，释放能量的能力逐渐变小。在文献[12]中描述了弹性能量恢复率η和弹性回弹能力ζ的关系，即

Eelastic/Etotal=1-hf/hmax=e/hmax

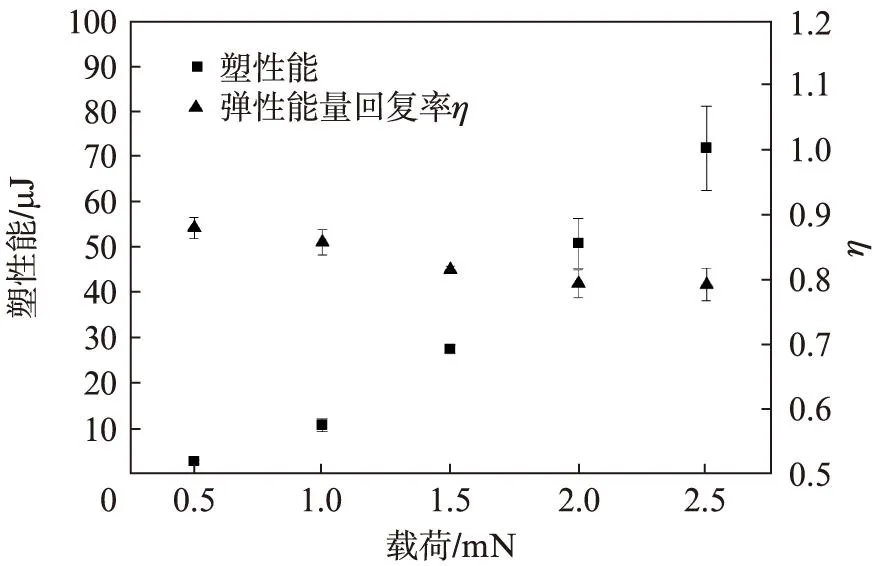
图5　塑性能与弹性能量恢复率Fig.5　Ratio of plastic energy and elastic energy recovery

通过分析可以得到: 若样品为完全弹性材料，加载曲线和卸载曲线完全重合，样品不存在塑性变形，弹性能等于总能量，弹性回弹为最大压入深度；或若样品为完全塑性材料，卸载曲线与位移轴垂直，弹性变形为零，不存在弹性回弹量，塑性能等于总能量，只有上述情况下文献中的关系成立；而材料具有弹塑性性能时，Eelastic/Etotal≠e/hmax，对于碳纤维材料其弹性能量恢复率小于弹性回弹能力，Eelastic/Etotal

4结论

通过纳米压痕测试法探讨了碳纤维的弹塑性性能，得到了载荷在0.5mN和2.5mN下非线性载荷和位移曲线，描述了其弹塑性行为，通过载荷/位移曲线得到材料在最大载荷处Pmax下的位移hmax、压痕接触深度hc以及卸载后由于塑性变形而形成的残留压痕深度hf。由于碳纤维材料的弹性回弹特性，其弹性回弹量e随着载荷的增加而逐步增加，但回弹能力ζ将随着载荷的增加而逐渐下降。加载行为就是对材料做功并储存塑性能量，卸载行为是弹性能量的释放，使材料的总能量发生变化，材料的塑性变形能可表现为材料储存能量的能力，碳纤维的塑性变形能即材料储存能量的能力将随着载荷的增加而增加，而弹性能量恢复率η即材料释放能量的能力随着载荷的增加而逐渐减少。对于碳纤维材料其弹性能量恢复率η小于弹性回弹能力ζ，即η<ζ。

参考文献：

[1]Oliver W C,Pharr G M.An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].Journal of Materials Research,1992,7(6): 1564-1583.

[2]Ye N,Komvopoulos K.Indentation analysis of elastic-plastic homogeneous and layered media: criteria for determining the real material hardness[J].Journal of Tribology,2003,125(4): 685-691.

[3]杨敏,孙晋良,任慕苏,等.三向正交编织碳/碳复合材料中碳纤维微区的弹性模量和纳米硬度[J].机械工程材料,2013,37(5): 76-79.

[4]赵军,王亚楠,王智,等.纳米压痕法测量经深冷处理后铝青铜的硬度和弹性模量[J].热加工工艺,2011,40(1): 10-12.

[5]黎业生,汪伟.纳米压痕法测量Cu膜的硬度和弹性模量[J].金属学报,2010,46(9): 1098-1102.

[6]Guillonneau G,Kermouche G, Bec S, et al.Determination of mechanical properties by nanoindentation independently of indentation depth measurement[J].Journal of Materials Research,2012,27(19): 2551-2560.

[7]Bolshakov A,Pharr G M.Influences of pile-up on the measurement of mechanical properties by load and depth sensing indentation techniques[J].Journal of Materials Research,1998,13(4): 1049-1058.

[8]Attaf M T.New ceramics related investigation of the indentation energy concept[J].Materials Letters,2003,57(30): 4684-4693.

[9]Cabibbo M,Ricci P.True hardness evaluation of bulk metallic materials in the presence of pile up: analytical and enhanced lobes method approaches[J].Metallurgical and Materials Transactions A,2013,44(1): 531-543.

[10]Rodrguez Pulecio S A, More Farias M C, Souza R M. Analysis of the tip roundness effects on the micro- and macroindentation response of elastic-plastic materials[J].Journal of Materials Research,2009,24(3): 1037-1044.

[11]Malzbendera J.Energy dissipated during spherical indentation[J].Journal of Materials Research,2004,19(6): 1605-1607.

[12]Jha K,Suksawang N, Lahiri D, et al.Evaluating initial unloading stiffness from elastic work-of-indentation measured in a nanoindentation experiment[J].Journal of Materials Research,2013,28(6): 789-797.

[13]Ma D,Ong C W.Further analysis of energy-based indentation relationship among Young’s modulus, nominal hardness, and indentation work[J].Journal of Materials Research,2010,25(6): 1131-1136.

[14]Yang R,Zhang T, Feng Y. Materials communications theoretical analysis of the relationships between hardness,elastic modulus,and the work of indentation for work-hardening materials[J].Journal of Materials Research,2010,25(11)： 2072-2077.

[15]Anthony C,Fischer-Cripps.Nanoindentation[M].New York: Springer,2011: 1-59.

Elastic-Plastic Level of Material Based on Indentation Energy

SUNYuan

(School of Mechanical Engineering, Shanghai Dianji University, Shanghai 200245, China)

Abstract:Using a nano-indentation method, the elastic and plastic deformation behavior of carbon fibers is studied. Curves of nonlinear load and displacement are obtained under a load of 500N and 2500N, with maximum indentation depth, contact depth, and residual depth. Elastic recovery and plastic energy of carbon fiber are calculated based on the load and displacement curves. Experimental results show that elastic recovery of carbon fiber increases with the increase of load, while the ability of elastic recovery decreases with the increase of the load. The plastic deformation energy increases with the increase of load, showing that the material energy storage capacity of carbon fiber increases with the increase of load. The recovery ratio of elastic energy decreases with the increase of the load, showing that the ability of release energy gradually decreases with the increase of load. The recovery ratio of elastic energy is less than the ability of elastic recovery.

Key words:curve of load and displacement; elastic recovery; plastic deformation energy

文献标志码:A

中图分类号:TB125

文章编号2095 - 0020(2015)01 -0008 - 05

作者简介：孙渊(1969-)，女，教授,博士，主要研究方向为机械制造及其自动化，E-mail: suny@sdju.edu.cn

基金项目：国家自然科学 资助(1080407)；上海市教育委员会科研创新项目资助(11YZ269)；上海市教育委员会重点学科建设项目资助(J51902)

收稿日期：2015 - 01 - 26