MIMO中继系统中基于不完全信道信息的线性预编码算法

陈小敏 朱益民 朱秋明 苏君煦

(1.南京航空航天大学电子信息工程学院,南京 210016; 2.南京航空航天大学 雷达成像与微波光子技术教育部重点实验室,南京 210016)



MIMO中继系统中基于不完全信道信息的线性预编码算法

陈小敏1,2朱益民1朱秋明1,2苏君煦1

(1.南京航空航天大学电子信息工程学院,南京 210016; 2.南京航空航天大学 雷达成像与微波光子技术教育部重点实验室,南京 210016)

针对采用放大转发中继技术的多输入多输出系统,提出一种基于不完全信道状态信息的中继预编码设计方案. 假设在中继端已知源-中继的全部信道状态信息,在中继-目的端的信道考虑信道估计误差及发射天线相关性,根据最小均方误差设计准则,推导获得目的端线性处理矩阵. 在中继端最大发射功率约束条件下,通过理论推导求得中继端线性预编码矩阵的闭式解. 数值仿真结果表明,在存在信道估计误差和天线相关性的条件下,所提方案能有效降低系统的误比特率和均方误差.

MIMO中继;放大转发;预编码;最小均方误差;误比特率

引 言

多输入多输出(Multiple-InputMultiple-Output,MIMO)技术可以明显提高系统容量和频谱利用率[1],而中继技术可以有效提高系统的传输能力和覆盖范围[2]. 研究表明,通过在源、中继和目的端配置多个天线,并结合MIMO处理技术可进一步提升系统的传输能力和容量[2-3]. 中继方式通常包括放大转发(Amplify-and-Forward,AF)和译码转发(Decode-and-Forward,DF)两种,其中AF方式由于实现简单、复杂度低,近年来受到了更多关注[3].

针对AF-MIMO中继系统,文献[4-7]在信道条件完全已知情况下,分别提出了中继端线性预编码方案;文献[8-10]研究了存在信道估计误差情况下的联合预编码方案,但其未考虑到多天线之间的相关性;文献[11-12]研究了基于天线相关性情况下的联合预编码方案,却未涉及到信道估计误差的影响.

对于实际AF-MIMO中继系统而言,不可避免地会存在信道估计误差和天线相关性,因此研究基于信道估计误差和发射天线相关性的中继线性预编码方案具有重要应用价值. 需要指出的是,文献[13]虽然给出了一种综合考虑信道估计误差和天线相关性的线性预编码方案,但该方案仅针对MIMO系统,并不适用于AF-MIMO中继系统.

本文以AF-MIMO中继系统为模型,综合考虑中继-目的端信道的估计误差和中继端发射天线的相关性,并以最小均方误差(MinimumMean-SquaredError,MMSE)为设计准则,分析了中继端线性预编码的设计方法,并通过理论证明给出了最优预编码矩阵和目的端线性处理矩阵.

1 系统模型

AF-MIMO中继系统模型如图1所示,它包括源、中继和目的端三部分. 令源、中继和目的端分别配置ns、nr和nd根天线,且满足ns≤nr≤nd条件. 同时,假设源和目的端之间距离较远,不存在直达路径,故需要通过中继协助来完成数据传输. 由于中继不能同时发送和接收信息,采用半双工方式,一次完整传输由两个时隙组成. 本文仅考虑平坦瑞利衰落MIMO信道,并且假设一次传输的两个时隙内信道状态保持基本不变.

图1 AF-MIMO中继系统模型

在第一个时隙内,源信号经过空间分集(Spatial Multiplexing, SM)向中继发送信号,中继端接收信号yr为

yr=H1x+n1.

(1)

在第二个时隙内,中继对接收信号进行线性处理,然后向目的端转发信号,转发信号s为

s=Gyr=G(H1x+n1).

(2)

其中,G∈Cnr×nr表示中继端的预编码矩阵. 中继转发的信号需满足中继最大功率约束为

P(G)=ε{ssH}

(3)

式中: tr[·]表示矩阵的迹;Pr为中继端最大功率.

目的端接收信号yd可表示为

yd=H2G(H1x+n1)+n2

=H2GH1x+H2Gn1+n2.

(4)

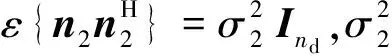
假设中继端完全已知源-中继的信道状态信息(Channel State Information, CSI),而中继-目的链路存在信道估计误差和发射天线相关性,故中继-目的信道可建模为[3]

(5)

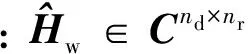
最终,目的端接收信号可表示为

(6)

式中,H和n分别表示等效信道矩阵和目的端总噪声,二者可分别表示为:

H

(7)

n

(8)

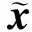
(9)

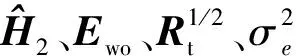
(10)

2 中继预编码算法设计

MSE代价函数可表示为[3-6]

(11)

结合式(9),简化式(11)为

(12)

式中:

RN

(13)

2.1 线性处理矩阵推导

对于式(12)而言,当中继预编码矩阵Gopt确定时,最优线性处理矩阵W也可唯一确定.

由∂J(Gopt,W)/∂WH=0,可得

(14)

将式(14)代入式(12)可得

(15)

进一步将式(13)代入式(15),化简后可得

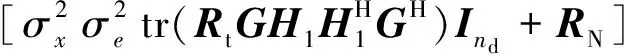
(16)

因此,中继预编码矩阵G的最优解问题可表示为

(17)

结合式 (12)和(17)可知,鉴于线性处理矩阵W可由中继预编码矩阵G确定,因此式(10)的最优化问题转向基于MMSE准则的中继预编码矩阵G优化问题.

2.2 中继预编码矩阵推导

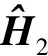
(18)

(19)

式中:U1、V1、U2和V2是酉矩阵;Λ1=diag(Λ1,1,Λ1,2,…,Λ1,ns)和Λ2=diag(Λ2,1,Λ2,2,…,Λ2,nr)分别是对角值依次递减的对角矩阵.

为了便于对角化式(16),中继预编码矩阵G可改写为[4]

(20)

Φ=diag(Φ1,Φ2,…,Φns)是一个ns×ns的对角矩阵.

然后,将式(18)～(20)代入式(16)及(13),可得

(21)

N

(22)

当A,B为N×N的正定矩阵时,存在如下关系式[17-18]

(23)

式中:特征值λi(A),λi(B)按降序排列;λmax(B)是矩阵B最大的特征值,令a为矩阵Rt最大特征值.

利用式 (21)～(23)改写式(17)的优化问题为式(24)所示,并利用卡罗需-库恩-塔克(Karush-Kuhn-Tucker,KKT)条件[19]求解,最终可得最优中继预编码矩阵如式(25)所示.

(24)

(25)

式中: (x)+=max(x,0); β的选定需要满足式(3). 当Φi幅度固定后,Φi的相位对式 (24)无影响.

3 数值仿真验证

当中继端完全已知源-中继信道状态信息,考虑中继-目的端存在信道估计误差和发射天线相关性的条件下,本节对前文获得的中继预编码方案进行仿真验证.同时,与文献[11]不考虑信道估计误差、文献[8]不考虑天线相关性和文献[4]不考虑信道估计误差和天线相关性的方案进行对比.

ri,j=ρ|i-j|.

(26)

图2和图3分别给出了中继MIMO系统的误比特率和均方误差性能比较图.从仿真结果看出:与

图2 误比特率性能比较

只考虑天线相关性、只考虑信道估计误差和均未考虑信道估计误差及天线相关性的中继预编码方案相比,本文提出方案确实可以获得更低的误码率(Bit Error Rate, BER)和MSE;而且值得注意的是,随着RSN,2的逐渐增大,其他三种方案的性能均会出现平缓的迹象,本文方案则继续保持下行趋势,性能优势更加突出.

图3 均方误差性能比较

4 结 论

针对AF-MIMO中继系统,假设在中继端已知源至中继的全部信道状态信息,在中继至目的端的信道考虑信道估计误差及发射天线相关性,本文提出了一种中继预编码方案. 根据MMSE准则,推导了理论表达式,并给出了线性处理矩阵和中继预编码矩阵的闭式解. 仿真结果表明,相对于仅考虑信道估计误差和仅考虑天线相关性等方案,本文方案能有效降低系统的误比特率和均方误差.

[1] TELATAR E. Capacity of multi-antenna Gaussian channels[J]. European Transactions on Telecommunications, 1999, 10(6): 585-595.

[2] WANG B, ZHANG J, HOST-MADSEN A. On the capacity of MIMO relay channels[J]. IEEE Transac-

tions on Information Theory, 2005, 51(1): 29-43.

[3] SANGUINETTI L, D'AMICO A, RONG Y. A tutorial on the optimization of amplify-and-forward MIMO relay systems[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(8): 1331-1346.

[4] GUAN W, LUO H. Joint MMSE transceiver design in non-regenerative MIMO relay systems[J]. IEEE Communications Letters, 2008, 12(7): 517-519.

[5] ZHANG B, WANG X, NIU K, et al. Joint linear transceiver design for non-regenerative MIMO relay systems[J]. Electronics letters, 2009, 45(24): 1254-1256.

[6] WANG R, TAO M. Joint source and relay precoding designs for MIMO two-way relaying based on MSE criterion[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1352-1365.

[7] MILLAR A P, WEISS S, STEWART R W. Tomlinson Harashima precoding design for non-regenerative MIMO relay networks[C]//2011 IEEE 73rdVehicular Technology Conference. Budapest, 2011: 1-5.

[8] 邹俊, 刘伟, 罗汉文, 等. 多进多出中继系统中基于失真信道估计的线性预编码[J]. 上海交通大学学报, 2011, 45(7): 1050-1053.

ZOU Jun, LIU Wei, LUO Hanwen, et al. Linear precoder design for amplify-and-forward MIMO relay systems with channel estimation errors[J]. Journal of Shanghai Jiaotong University:Science, 2011, 45(7): 1050-1053. (in Chinese)

[9]ZHANG L, CAI Y, ZHAO M, et al. Robust Tomlinson-Harashima precoding design in amplify-and-forward MIMO relay systems via MMSE criterion[C]//2013 IEEE Wireless Communications and Networking Conference. Shanghai, 2013: 2727-2732.

[10] MILLAR A P, WEISS S, STEWART R W. Robust transceiver design for MIMO relay systems with Tomlinson-Harashima Precoding[C]//2012 IEEE 20th Signal Processing Conference. Bucharest, 2012: 1374-1378.

[11] WAGNER J, RANKOV B, WITTNEBEN A. Large analysis of amplify-and-forward MIMO relay channels with correlated rayleigh fading[J]. IEEE Transactions on Information Theory, 2008, 54(12): 5735-5746.

[12] LOUIE R H Y, LI Y, SURAWEERA H A, et al. Performance analysis of beamforming in two hop amplify and forward relay networks with antenna correlation[J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 3132-3141.

[13] DING M, BLOSTEIN S D. MIMO minimum total MSE transceiver design with imperfect CSI at both ends[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1141-1150.

[14] 陈小敏, 徐大专, 虞湘宾, 等. Turbo-BLAST系统中天线选择和功率分配算法[J]. 电波科学学报, 2009, 24(3): 533-536.

CHEN Xiaomin, XU Dazhuan, YU Xiangbin, et al. Transmit antenna selection and power allocation algorithm for Turbo-Blast system[J]. Chinese Journal of Radio Science, 2009, 24(3): 533-536. (in Chinese)

[15] 陈小敏, 谭伟, 于晓丹, 等. 存在反馈延迟时V-BLAST系统的功率分配算法[J]. 电波科学学报, 2014, 29(6):1088-1093.

CHEN Xiaomin, TAN Wei, YU Xiaodan, et al. Power allocation algorithm for V-BLAST system based on MMSE detector with feedback delay[J]. Chinese Journal of Radio Science, 2014, 29(6):1088-1093.(in Chinese)

[16] 王子磊, 奚宏生, 盛延敏. 基于特征空间的MIMO天线选择算法[J].电波科学学报, 2006, 21(4): 518-524.

WANG Zilei, XI Hongsheng, SHENG Yanmin. Antenna selection algorithm in MIMO systems based on main eignvectors[J]. Chinese Journal of Radio Science, 2006, 21(4): 518-524.(in Chinese)

[17] XING C, MA S, WU Y C. Robust joint design of linear relay precoder and destination equalizer for dual-hop amplify-and-forward MIMO relay systems[J]. IEEE Transactions on Signal Processing, 2010, 58(4): 2273-2283.

[18] TSENG F S, CHANG M Y, WU W R. Joint Tomlinson-Harashima source and linear relay precoder design in amplify-and-forward MIMO relay systems via MMSE criterion[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1687-1698.

[19] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge:Cambridge University Press, 2009.

Linear precoding scheme for MIMO relay system with imperfect channel state information

CHEN Xiaomin1,2ZHU Yimin1ZHU Qiuming1,2SU Junxu1

(1.CollegeofElectronicandInformationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China; 2.KeyLaboratoryofRadarImagingandMicrowavePhotonics,Astronaut,MinistryofEducation,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

A linear pre-coding algorithm is proposed for the amplify-and-forward MIMO relay system with imperfect channel state information. In the proposed scheme, optimal relay precoding matrix is deduced based on the assumption that the full channel state information (CSI) of the source-relay link is acquired at the relay and the estimation errors and the antenna’s correlation information of the relay-destination link is considered. The linear processing matrix at the receiving terminal is first derived based on the minimum mean squared error (MMSE) criterion and then the closed form of the optimal relay precoding matrix is deduced with the maximum power constraint at the relay station. The numerical results show that the proposed scheme achieves better performance in terms of both bit error rate (BER) and mean squared error (MSE) compared with other schemes.

MIMO-relay; amplify-and-forward; precoding; MMSE; BER

10.13443/j.cjors. 2014101502

2014-10-15

中国博士后科学基金(2013M541661)； 江苏高校优势学科建设工程资助项目

TN98

A

1005-0388(2015)05-0878-06

陈小敏 (1975-),女,江苏人,博士,南京航空航天大学副教授,研究领域为无线通信、空时编码的信号检测和链路自适应技术方向研究等.

朱益民 (1990-),男,江苏人,硕士研究生,研究方向为MIMO中继系统预编码及功率分配.

朱秋明 (1979-),男,江苏人,博士,南京航空航天大学副教授,研究领域为MIMO无线信道建模和模拟、航空数据链技术等.

苏君煦 (1993-)，男，湖南人，硕士研究生，研究方向为MIMO无线信道建模和模拟。

陈小敏, 朱益民, 朱秋明, 等. MIMO中继系统中基于不完全信道信息的线性预编码算法[J]. 电波科学学报,2015,30(5):878-883.

CHEN Xiaomin, ZHU Yimin, ZHU Qiuming, et al. Linear precoding scheme for MIMO relay system with imperfect channel state information[J].Chinese Journal of Radio Science,2015,30(5):878-883. (in Chinese). doi:10.13443/j.cjors. 2014101502

联系人： 陈小敏 E-mail: chenxm402@nuaa.edu.cn