基于免疫PID的漂浮式小型天线扰动抑制研究
姚志英 曹海青 王渝
(1.北京物资学院物流学院,北京 101149;2.首都经济贸易大学信息学院,北京 100070; 3.北京理工大学自动化学院,北京 100081)
基于免疫PID的漂浮式小型天线扰动抑制研究
姚志英1曹海青2,3王渝3
(1.北京物资学院物流学院,北京 101149;2.首都经济贸易大学信息学院,北京 100070; 3.北京理工大学自动化学院,北京 100081)
针对小型天线漂浮于海面所受到的各种扰动,研究了一种基于免疫反馈原理的免疫比例-积分-微分(Proportional-Integral-Derivative,PID)控制器,应用于海面小型漂浮式动载天线跟踪卫星的姿态控制中,保证扰动环境下漂浮式天线与卫星间高质量通信.研究小型天线在海洋中漂浮时所受到海洋环境扰动的类型和特点;将免疫反馈原理和PID控制器相结合组成免疫PID控制器,应用于抑制海洋环境扰动对小型漂浮天线姿态控制的影响;以小型天线方位系统控制为例,通过Matlab仿真和半实物仿真验证了免疫PID控制器可以很好地实现海洋环境扰动下小型天线的方位控制,可很好地抑制各种扰动对天线方位调整的影响,保证漂浮式天线与卫星间的高质量通信.
姿态控制;扰动抑制;免疫反馈原理;免疫PID
引 言
研究一种可用于隐蔽式海上军事侦察通信的小型漂浮式卫星天线,漂浮式天线相比传统的海事卫星天线体积小、质量小、隐蔽性高[1],当天线漂浮于一望无际的海面时,因其较好的隐蔽性不易被发现.体积小、质量小,故漂浮式天线的惯性小、阻尼系数小,使得天线系统的漂浮状态对海洋环境扰动较为敏感,增加了天线姿态控制的难度.
小型漂浮式卫星天线漂浮于海面的运动是一个十分复杂的六自由度摇荡运动,各个运动间的耦合性较强,这样就增加了以天线系统的受力分析为基础,通过解非线性耦合方程方法确定天线姿态信息的难度.目前依据小型漂浮式天线系统姿态信息进行天线指向控制的方法主要是通过以下两种方式来实现的:方法一是利用全球定位系统(Global Position System, GPS)实时测量出天线系统的位置信息,根据位置信息和目标卫星的星历数据解算出天线指向偏离卫星最佳通信区域的偏差,将此偏差作为天线姿态控制的控制量,实现天线姿态的控制,关于这种方法的详细研究请参考文献[2];方法二是利用集成于天线系统上的航姿测量子系统测量出天线系统实时姿态信息,通过比较当前姿态与卫星最佳通信姿态间的偏差,将此偏差作为天线姿态控制的控制量,进行天线姿态的控制,有关这种方法的详细应用请参考文献[3].本文将免疫反馈控制用于优化文献[2]所研究的方法一的控制效果,究其原因如下:在对方法一的进一步研究中,发现方法一对海洋涌浪的扰动具有较好的抑制能力,而当遭遇海洋环境的其他扰动时,虽然也能实现天线姿态的控制,但其扰动抑制能力不太理想,尤其是在扰动发生时刻和扰动消失的瞬间,扰动对系统的影响较大.
1 海洋环境中的扰动
小型天线漂浮于海面时,其姿态受到海洋环境中各种扰动的影响,增加了天线姿态控制的难度.海洋环境的扰动主要包括涌浪扰动、突发扰动、随机扰动和复杂扰动.
1.1 涌浪扰动
漂浮于海面的小型天线时刻受到海洋风浪扰动的影响,风浪按其特征分为风波和涌浪,其中风波紊乱而不规则,持续时间短;涌浪波长较长、波高较小,比较规则,持续时间长.从统计意义上讲,不规则的风波可用无数个不同波幅和波长的单元规则波叠加组成,可以通过研究涌浪扰动来研究风浪对海洋漂浮天线的影响.涌浪扰动属于长峰波可以用平面波表示为
d(t)=ζacos(kξ+ωt).
(1)
式中:ζa为波幅;ξ为波面偏离静水面的高度;k为波数,k=2π/λ=ω2/g,ω为圆频率,λ为波长,波周期TB=2π/ω.本文研究风级不大于4级的中小涌浪的扰动,中小涌浪的有义波高h1/3小于2 m,波长小于60 m,周期小于6.2 s,风速小于19节,约为9.7 m/s[2].
1.2 突发扰动
突发扰动是指海洋环境中的生物体和其他漂浮物的运动所引起的扰动,这种扰动作用时间不长,具有一定的幅值,可用式(2)表示为
(2)
但突发扰动何时发生并无规律可循.
1.3 随机扰动
随机扰动也被称为随机噪声,具有不确定性和随机性,在本研究中随机噪声仅限于高斯白噪声,服从正态分布.海洋环境中的随机扰动可用一定的作用时间和扰动最大幅值来表示,以图1为例来说明海洋环境中的随机扰动,图中的扰动作用时间为2s到3s,最大幅值为0.02°.
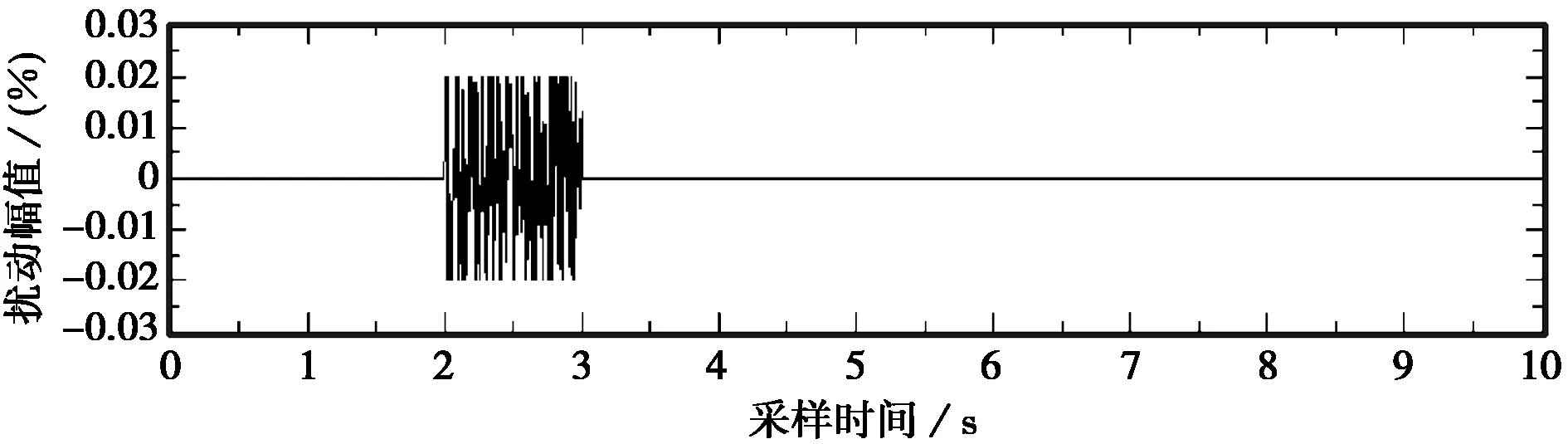
图1 随机扰动
1.4 复杂扰动
海洋环境中的复杂扰动可以看作由多个突发扰动和涌浪扰动叠加而成,可用式(3)表示
(3)
式中:Ai为扰动幅值,i=1,…,n,n为自然数;Bj为扰动幅值;ωj为圆频率;φj为初相位,j=1,…,m,m为自然数;t2-t1为扰动作用的持续时间.
1.5 扰动抑制指标
为了衡量免疫比例-积分-微分(Proportional-Integral-Derivative,PID)控制器对海洋环境扰动抑制效果,以保证扰动环境下漂浮天线与目标卫星间高质量通信,本文在参考文献[4-5]相关内容的基础上重新定义了扰动抑制率和扰动消失影响时间作为考核免疫PID控制器的扰动抑制能力的评价指标.
定义1 扰动抑制率DR是衡量扰动抑制效率的物理量,设系统扰动的最大幅值为A,系统在无扰动情况下的输出幅值为A1,系统在叠加扰动过程中的输出最大幅值为A2,则扰动抑制率可表示为
(4)
定义2 扰动消失影响时间是指当扰动消失后,因惯性的原因扰动作用效果不可能随扰动一起立即消失,而是对系统的影响会持续一段时间,所持续的这段时间即为扰动消失影响时间.
根据扰动抑制率和扰动消失影响时间的定义可知,扰动抑制率越大且扰动消失影响时间越小表示控制策略的扰动抑制效果较好.
2 人工免疫
2.1 免疫反馈
免疫系统是生物体的重点防御机构,在维持生物体正常生理平衡过程中起着十分重要的作用;当有异己成分(抗原)入侵生物体后,免疫系统可以快速地做出反应,有效地排除异己成分对生物体的影响,并在异己成分清除后快速地使生物体恢复到系统的平衡状态;生物体免疫系统的主要工作原理为免疫反馈原理,免疫反馈原理主要通过免疫反应来实现,免疫反应通过不同T细胞的子群间相互反应来实现,其中抑制性T细胞(Ts)和辅助性T细胞(Th)是免疫反应中最主要的两个子群;当抗原进入生物体被抗原呈递细胞消化后,将信息传递给Th细胞和Ts细胞,并激活Th细胞,Ts细胞抑制Th细胞的产生,而后Ts细胞和Th细胞共同作用激活B细胞产生抗体,当抗原较多时,Th细胞较多,Ts细胞较少,产生的抗体B较多,随着抗原的减少,Ts细胞增多,抑制Th细胞的产生,则B细胞也随之减少,经过一段时间后,免疫反馈系统便趋于平衡[6-7].免疫反馈原理如图2所示.

图2 免疫反馈原理
2.2 基于免疫反馈原理的控制器
人工免疫系统是基于免疫系统的机理和免疫学理论发展起来的.众所周知生物免疫反馈原理可以识别和分离出异己成分,对异己入侵做出快速的反应,维持生物体的平衡.基于免疫反馈原理可设计有效的反馈控制系统,快速检测、分离和抑制系统的扰动和不确定性.本文将生物免疫系统的免疫反馈原理应用于漂浮式卫星天线系统方位伺服控制中,旨在改善文献[2]所研究的分区PID控制器对海洋环境适应性较差的现状,提高天线姿态控制的鲁棒性.
在生物免疫系统的免疫反馈过程中,抗体的数量是由Th细胞的促进作用和Ts细胞的抑制作用共同作用的结果.设第i代的抗原数量为c(i),由抗原对Th细胞的刺激输出为Th(i),Ts细胞对B细胞的影响为Ts(i),则B细胞所受到的总刺激为
S(i)=Th(i)-Ts(i).
(5)
式中:Th(i)=k1c(i);Ts(i)=λk2f(Δs(i))c(i).若以c(i)作为偏差e(i),B细胞所接收的总刺激作为总输入u(i),则反馈控制律为
u(i)=k1c(i)-λk2f(Δs(i))c(i)
=k{1-ληf[Δu(i)]}e(i).
(6)
式中:k=k1为控制反应速度;η=k2/k1为控制稳定效果;f(·)为非线性函数.式(6)所示的免疫反馈原理所组成的控制器其实质是一个非线性P型控制器,其控制效果取决于参数k、λ、η和非线性函数f(·)[8].参考文献[7,9]定义该非线性函数为
(7)
a为作用系数且a>0.取不同的a值,非线性函数f(x)的变化情况如图3所示.由图可知:当a变大时,非线性函数f(x)的取值范围变小;当a=10时,f(x)的取值范围为[-0.6,0.6];当a=20时,f(x)的取值范围为[-0.3,0.3].

图3 非线性函数f(x)随参数a的变化情况
文献[7,9]对免疫反馈控制律在实际控制系统中应用时采用了图4所示的免疫反馈控制器(Immune Feedback Controller,IFC),并将式(6)所表示的免疫反馈控制律转化为
u(i)=k[1-ληf(·)].
(8)
式中:λ代表免疫调节过程不同阶段的调节因子, 当λ=-1时表示免疫刺激阶段,λ=0时表示免疫稳定阶段,λ=1时表示免疫抑制阶段.在实际应用时设计了最大偏差值e0和最小偏差值e1,在免疫初始响应(大抗原)阶段时,|ek|>e0,抗体细胞快速增长,此时λ=-1表示免疫反馈处于刺激阶段;在抗体高度集中阶段,e1<|ek| (9) 事实上,抗原和抗体在生物免疫反馈过程中的变化情况如图5所示.在生物免疫早期抗原浓度较大,必须及时清除,并刺激抗体产生,因此按照浓度的大小取不同的调节因子λ更加符合生物免疫过程变化;在生物免疫应答抗原分解期抗原浓度下降抗体浓度增加,为了很好地抑制抗体浓度过度增加,也应该根据抗原和抗体的变化情况来进行调节因子λ的取值,故用式(9)所示的方法求取调节因子λ的值存在一定的不合理性,本文采用式(8)所示的P型免疫反馈律,其中调节因子λ的取值通过式(10)来确定: (10) 图4 免疫反馈控制器 图5 免疫反馈过程抗原和抗体的变化 3.1 天线方位免疫PID控制器 本文将PID控制器和免疫反馈控制器相结合组成复合控制器,用于改善基于局域预测的天线方位控制系统扰动抑制的能力.所采用的复合控制器结构如图6所示. 图6 天线方位免疫PID控制器 3.2 天线方位免疫PID控制器仿真研究 为了测试复合控制器的性能和扰动抑制能力,利用Matlab建立了免疫PID的天线方位伺服控制器模型,并在此仿真模型上做了如下的性能测试实验,在实验过程中d=2,a=10,k1=3,η=0.8,e0=0.6,e1=0.1. 实验一 系统在无扰动的情况下启动后,输入阶跃信号,系统的响应情况如图7所示.可得改进后的天线方位伺服控制器的阶跃响应时间比原来减少了0.1 s,超调量大幅度降低几乎接近于零,因此改进后天线方位伺服控制器的性能优于原来的基于分区PID的天线方位伺服控制器. 实验二 系统启动输入阶跃信号后,扰动输入端输入 d(t)=0.3 cost (11) 所示的涌浪扰动,系统的输出如图8所示.可得改进后天线方位伺服控制器可以很好地抑制系统的涌浪扰动,扰动抑制率已达到100%,很显然基于免疫的PID控制比分区PID的控制效果更好. 图7 天线方位免疫PID控制器的阶跃响应 图8 涌浪扰动下天线方位免疫PID控制器的阶跃响应 实验三 系统启动输入阶跃信号后,扰动输入端输入图1所示的随机扰动,则系统的输出如图9所示.可得改进后基于免疫PID控制的天线方位伺服控制器可以很好地抑制随机扰动,扰动抑制率达90%以上,且扰动消失影响时间小于0.1 s. 实验四 在系统启动输入阶跃信号后,扰动输入端输入 (12) 所示的突发扰动,则系统的输出如图10所示.可得改进的天线方位伺服控制器可以很好地抑制突发扰动,扰动抑制率达90%以上,而且在小于0.3s内系统就能保持稳定的输出;无论是扰动抑制还是对扰动的响应均比原来有明显的提高.通过上述仿真试验可知,基于免疫反馈控制器和PID所组成的复合控制器的性能优于文献[2]所研究的小型漂浮式卫星天线的方位伺服控制器. 图9 随机扰动下天线方位免疫PID控制器的阶跃响应 图10 突发扰动下天线方位免疫PID控制器的阶跃响应 3.3 半实物仿真研究 半实物仿真平台由卫星天线子系统、六自由度摇摆台和小车组成,卫星天线子系统由天线、通信子系统、姿态控制子系统和人机交互子系统组成,实现天线与卫星间的高质量通信;六自由度摇摆台主要通过摇摆台的运动来实现海洋涌浪的运动;小车用来模拟海水的静水流动情况,即通过小车的平动来模拟海水的流动情况;此外在半实物仿真过程中通过在路面设置一些小车可越过的障碍物来模拟海洋环境中的突发扰动;通过在测试路面的某一段洒落一些小的石块来模拟海洋环境中的随机扰动;在测试过程中将卫星天线子系统安装在六自由度摇摆台上,然后一并固连接于小车上. 在北京地区进行了半实物仿真测试,测试时长30min,测试的目标卫星为亚太VI,小车以2m/s的速度沿直线行进,六自由度摇摆台从测试开始5min到20min内按照ξ=2costm/s的规律做摇摆运动,模拟海洋环境中的涌浪;在测试路面的1 200、1 440、1 800、2 160、2 200、2 400m等处设置了高度不等的障碍物模拟海洋环境中的突发扰动;在测试路面的500m到800m、2 000m到2 600m随机洒落了一些最大直径为0.02m、最小直径为0.005m大的石子,模拟海洋环境中随机扰动;此外在1 200m到3 600m的路面旁边有多个分布不均匀的树和广告牌也会对天线进行遮挡.测试过程采用自发自收的模式,发射频率为1 132MHz,接收频率为1 134MHz,发射带宽为1MH,发射信号为-19dB(发射功率已饱和),功放器功率为40W;采用Modem来接收卫星的信标信号,在多次测试后取其中一次测试结果与文献[2]中方法在同样环境下测试的情况进行比较,具体情况如图11所示.在测试过程中通过Modem所接收到的卫星信标信号的值在5.5dB和7.8dB之间变化,可以保证天线与卫星间的高质量通信.由图11可知天线方位免疫PID控制器的控制效果优于文献[2]中分区PID控制器的控制效果,可以很好地实现海洋环境中各种扰动的抑制,保证天线与卫星间的高质量通信. 图11 天线方位免疫PID控制半实物仿真结果 本文研究了由免疫反馈控制器和PID控制器所组成的免疫PID控制器,旨在改善文献[2]中所研究的小型漂浮式卫星天线方位伺服控制器对海洋环境中不同扰动的鲁棒性较差的不足;根据生物免疫的原理,设计了免疫反馈控制器,在免疫反馈控制器的设计中采用了新方法确定免疫调节因子的λ值,使得免疫调节因子λ值在免疫反应过程中是一个实时变化的值,这更加符合生物免疫的变化过程;由免疫反馈控制器IFC和PID控制器组成的免疫PID控制器能实现小型漂浮式卫星天线的方位伺服控制,通过仿真研究证实了免疫PID控制器可以很好地抑制海洋环境中的各种扰动对天线方位控制的影响,其整体控制性能优于文献[2] 中所研究的分区PID控制器的性能,能保证天线与卫星间的高质量通信. [1] 曹海青, 王渝, 方建军, 等.一种小型漂浮式天线基座静力学特性研究[J]. 北京理工大学学报:自然科学版, 2014, 34(8): 790-795. CAOHaiqing,WANGYu,FANGJianjun,etal.Theresearchonstaticcharacteristicsofanovelsmallfloatantennabase[J].TransactionsofBeijingInstituteofTechnology, 2014, 34(8): 790-795.(inChinese) [2] 曹海青, 王渝, 杜明芳, 等. 基于局域预测的动载天线伺服控制策略研究[J]. 电波科学学报, 2014, 29(1): 106-113. CAOHaiqing,WANGYu,DUMingfang,etal.Researchonthecontrolpolicyofthemovingantennaservosystembasedonlocalprediction[J].ChineseJournalofRadioScience, 2014, 29(1): 106-113. (inChinese) [3] 曹海青, 王渝, 杜明芳, 等. 小型漂浮式卫星天线自抗扰控制器研究[J]. 电波科学学报, 2014, 29(5): 833-838. CAOHaiqing,WANGYu,DUMingfang,etal.Activedisturbancerejectioncontrollerforsmall-sizedfloatingantenna[J].ChineseJournalofRadioScience, 2014, 29(5): 833-838.(inChinese) [4] 李锦英, 付承旈, 于伟. 直接驱动系统中力矩扰动的抑制[J]. 哈尔滨理工大学学报, 2011, 16(4): 78-81. LIJinying,FUChengyu,YUWei.RejectionofTorquedisturbanceindirectdrivessystem[J].JournalofHarbinUniversityofScienceandTechnology, 2011,16(4): 78-81.(inChinese) [5] 方强,马杰, 毕运波, 等. 基于扰动观测器的电动负载模拟器控制系统设计[J].浙江大学学报: 工学版, 2009, 43(11):1958-1964. FANGQiang,MAJie,BIYunbo,etal.Disturbanceobserverbasedcontrollerdesignforelectricdynamicloadsimulator[J].JournalofZhejiangUniversity:EngineeringScience, 2009, 43(11):1958-1964. (inChinese) [6]YUANGuili,LIUJizhen.Thedesignfortheboilerdrumlevelsystembasedonimmunecontrol[J].JournalofComputers, 2012, 7(3): 749-754. [7]JIAHeming,SONGWenlong,WANGHaitao,etal.ImmunePIDalgorithmofwooddryingcontrolsystem[J].InternationalJournalofAdvancementsinComputingTechnology, 2012, 4(9): 248-258. [8] 丁永生, 任立红.一种新颖的模糊自调整免疫反馈控制系统[J]. 控制与决策, 2000, 15(4): 443-446+450. DINGYongsheng,RENLihong.Anewfuzzyself-tuningimmunefeedbackcontrolsystem[J].ControlandDecision, 2000,15(4): 443-446+450. (inChinese) [9] 谈英姿, 沈烔, 吕震中.免疫PID控制器在汽温控制系统中的应用研究[J].中国电机工程学报, 2002, 22(10): 148-152. TANYingzi,SHENJiong,LÜZhenzhong.StudyofimmunePIDcontrollerforsuperheatedsteamtemperatureandcontrollersystem[J].ProceedingsoftheCSEE, 2002, 22(10): 148-152.(inChinese) Disturbance rejection of the floating small-size antenna based on the immune PID YAO Zhiying1CAO Haiqing2,3WANG Yu3 (1.SchoolofLogitics,BeijingWuziUniversity,Beijing101149,China; 2.InformationSchool,CapitalUniversityofEconomicsandBusiness,Beijing100070,China; 3.SchoolofAutomation,BeijingInstituteofTechnology,Beijing100081,China) An immune proportional-integral-derivative(PID) controller based on the immune feedback mechanism is studied, which is applied in the process of the attitude control under all kinds of disturbances on sea to ensure the communication between the antenna and the satellite with high quality when the floating small-sized antenna tracks the target satellite. The various disturbances are studied and the immune PID controller based on the immune feedback mechanism and PID is designed to reject the disturbances on sea which affect the attitude control of the floating small-sized antenna seriously. Taking the azimuth control of the floating small-sized antenna as an example, MATLAB simulation and hardware-in-loop simulation validate the immune PID controller can realize the azimuth control under the disturbances, reject the influence of the disturbances and ensure the communication with high qualitybetween the floating small-sized anten-na and the target satellite. attitude control; disturbance rejection; immune feedback mechanism; immune PID 10.13443/j.cjors. 2014112501 2014-11-25 北京物资学院高级别科研项目培育基金(No.GJB20141006) TP273 A 1005-0388(2015)05-0936-07 姚志英 (1977-),女,江苏人,博士,讲师,北京物资学院教师,主要从事智能控制算法和物联网技术研究. 曹海青 (1976-),男,山西人,博士,讲师,首都经济贸易大学教师,主要从事信息通信控制、自动控制算法和非结构化信息管理研究. 姚志英,曹海青,王渝.基于免疫PID的漂浮式小型天线扰动抑制研究[J]. 电波科学学报,2015,30(5):936-942. YAO Zhiying, CAO Haiqing, WANG Yu. Disturbance rejection of the floating small-size antenna based on the immune PID[J]. Chinese Journal of Radio Science,2015,30(5):936-942. (in Chinese). doi: 10.13443/j.cjors. 2014112501 联系人: 姚志英 E-mail: public2008_8@sina.com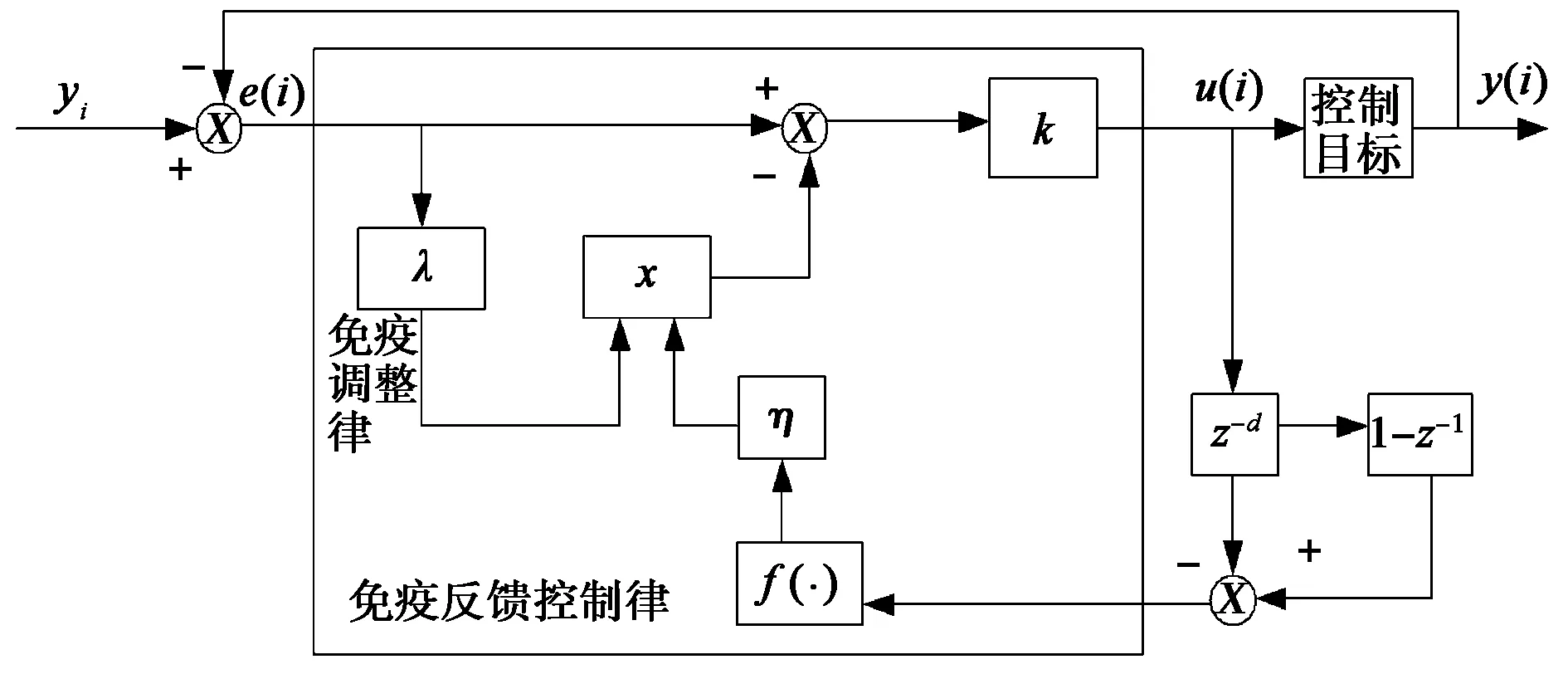

3 基于免疫PID的天线方位控制系统





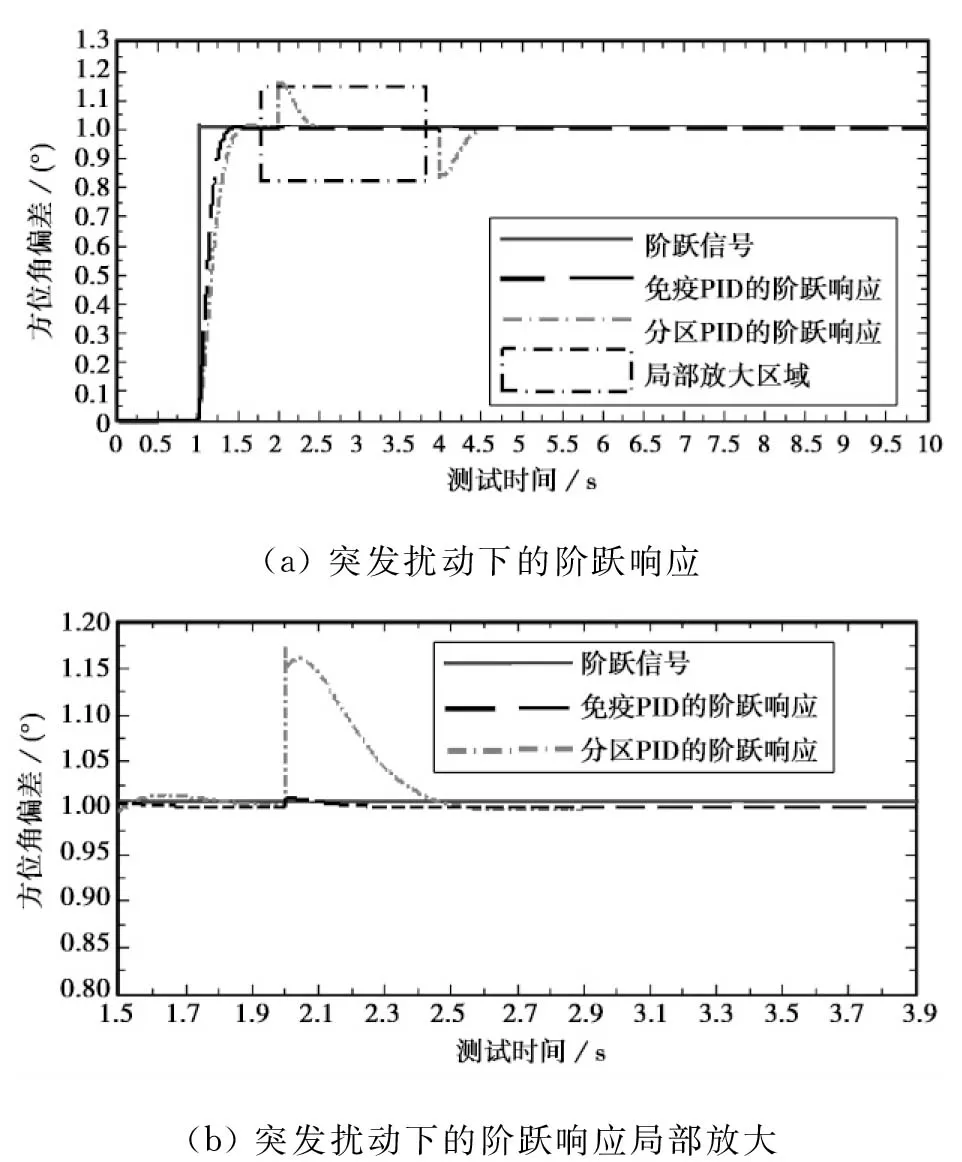

4 结 论



