轮换对称性在积分中的应用

秦勇

(常州工学院理学院，江苏常州213002)



轮换对称性在积分中的应用

秦勇

(常州工学院理学院，江苏常州213002)

利用对称性计算积分在一般“高等数学”的教材中均未提及，主要在一些考研数学辅导书或数学竞赛辅导书上有介绍。了解用对称性计算积分对改进“高等数学”的教学、简化积分的计算过程及提高学生的解题运算能力都有着实际的意义。对称性计算积分主要包括两方面[1]：一是积分区域关于坐标面、坐标轴和原点对称情况下被积分函数具有奇偶性的积分；二是积分区域关于积分变量具有轮换对称性情况下的积分。对于第1种情况比较好理解，因为多元函数的积分可以视为定积分在对称区间上积分的推广，而对于第2种情况则没有简单的理解方法且有关的结论也没有给出证明。

本文给出积分区域关于积分变量具有轮换对称性情况下积分的有关结论并给出证明，最后介绍其在计算积分中的一些应用。

1定理

定义设Ω⊆R3，如果∀(x,y,z)∈Ω，都有(z,x,y),(y,z,x)∈Ω，则称区域Ω关于变量x,y,z具有轮换对称性。

引理设区域Ω关于变量x,y,z具有轮换对称性，则存在Ω上的一个一一变换[2]。

证明因为Ω关于x,y,z具有轮换对称性，所以∀(x,y,z)∈Ω，有(z,x,y),(y,z,x)∈Ω，定义σ(x,y,z)=(z,x,y)∈Ω。∀(x1,y1,z1)，(x2,y2,z2)∈Ω,若(x1,y1,z1)=(x2,y2,z2)，则有x1=x2，y1=y2，z1=z2，从而(z1,x1,y1)=(z2,x2,y2)，即σ(x1,y1,z1)=σ(x2,y2,z2)，所以σ是Ω到Ω的一个映射，从而σ是Ω上的一个变换。∀(x1,y1,z1),(x2,y2,z2)∈Ω，若σ(x1,y1,z1)=σ(x2,y2,z2)，即(z1,x1,y1)=(z2,x2,y2)，从而有z1=z2，x1=x2，y1=y2，故(x1,y1,z1)=(x2,y2,z2))，所以σ是Ω到Ω的单射。∀(x,y,z)∈Ω，因为Ω关于x,y,z具有轮换对称性，所以(z,x,y),(y,z,x)∈Ω，因而存在(y,z,x)∈Ω，使σ(y,z,x)=(x,y,z)，所以σ是Ω到Ω的满射，从而σ是Ω到Ω的双射，因此σ是Ω上的一一变换。

定理1设积分区域Ω关于x,y,z具有轮换对称性，则有

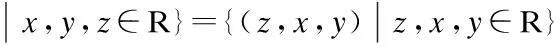
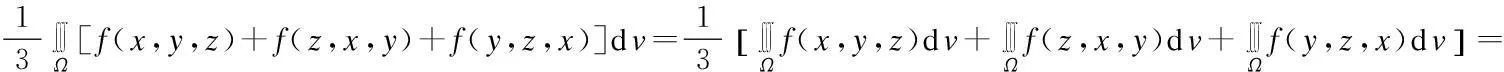
因此

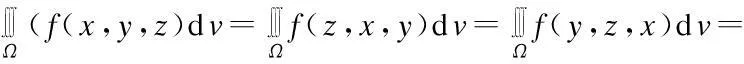
推论设积分区域Ω关于x,y,z具有轮换对称性，则有

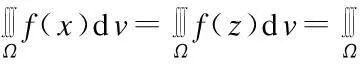
命题区域D关于变量x,y具有轮换对称性的充分必要条件是区域D关于直线y=x是对称的。

证明充分性：因为∀(x,y)∈D，点(x,y)关于直线y=x对称的点为(y,x)，又D关于直线y=x对称，所以(y,x)∈D，因此D关于变量x,y具有轮换对称性。

必要性：若D关于变量x,y具有轮换对称性，则∀(x,y)∈D，有(y,x)∈D，又点(x,y)与点(y,x)关于直线y=x是对称的，所以区域D关于直线y=x对称。

由定理1和命题可得以下定理。

定理2[3]设区域D关于变量x,y具有轮换对称性，则有

②设区域D位于直线y=x的上半部分为D1，下半部分为D2，则：

对于第1类曲线和曲面积分，同理可得定理3。

定理3设曲线Γ关于变量x,y,z具有轮换对称性，则有

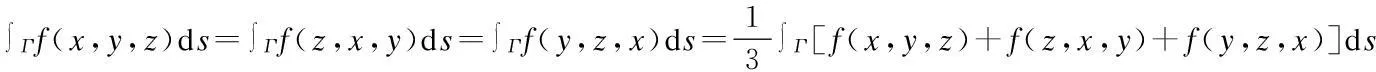
定理4[3]设平面曲线L关于变量x,y具有轮换对称性，则有

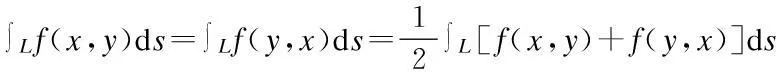
②设平面曲线L在直线y=x的上半部分为L1，下半部分为L2，则:

定理5设曲面∑关于变量x,y,z具有轮换对称性，则有

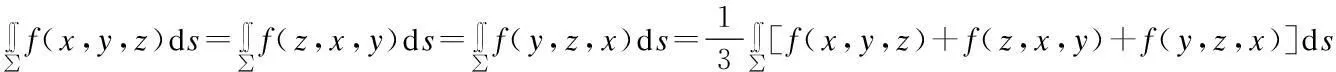
需要指出：由于第2类曲线积分中的曲线与第2类曲面积分中的曲面都是有向的，所以轮换对称性的有关结论对于第2类曲线积分与第2类曲面积分类似的结论是不成立的。

2应用

解：因为积分区域Ω关于x,y,z具有轮换对称性，由定理1，得

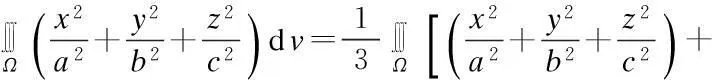
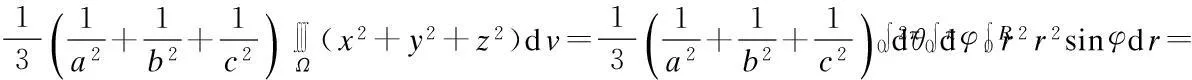
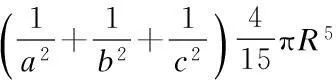
解：因为积分区域D关于变量x,y具有轮换对称性，由定理2，得

例3设函数f(x)在区间[0,2]上连续，并设∫20f(x)dx=a，求∫20dx∫2xf(x)f(y)dy。

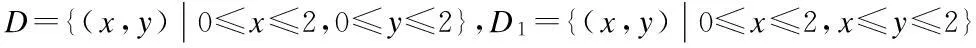
解：因为曲线积分Γ关于变量x,y,z具有轮换对称性，由定理3，得

解：因为积分曲线L关于变量x,y具有轮换对称性，由定理4，得

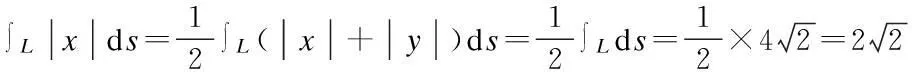
解：因为曲面积分∑关于变量x,y,z具有轮换对称性，由定理5，得

[参考文献]

[1]毛纲源.最新考研数学(一)常考题型解题方法技巧归纳[M].武汉：华中科技大学出版社,2008：164-171.

[2]张禾瑞,郝鈵新.高等代数[M].4版.北京：高等教育出版社,2000.

[3]秦勇.再谈轮换对称性[J].高等数学研究,2007,10(2)：20-22.

责任编辑：周泽民

本刊声明

为适应我国信息化建设，扩大本刊及作者知识信息交流渠道，本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。作者文章著作权使用费与稿酬本刊一并支付。作者向本刊提交文章发表的行为即视为同意本刊上述声明。中国学术期刊(光盘版)电子杂志社将免费提供作者文章引用统计分析资料。如作者不同意文章被收录，请在投稿时告知本刊，本刊将适当处理。

谢谢合作！

摘要：证明了轮换对称性的有关结论，并阐述了其在积分中的一些应用。

关键词：轮换对称性；积分；区域；变量；双射

Application of Cyclosymmetric Property in IntegralQIN Yong

(School of Science,Changzhou Institute of Technology,Changzhou 213002)

Abstract：This article has proved some conclusions about cyclosymmetric property and introduced applications of cyclosymmetric property in integral.

Key words：cyclosymmetric property；integral；range；variable；bijection

中图分类号：O172

文献标志码：A

文章编号：1671-0436(2015)03-0062-04

作者简介：秦勇(1958—)，男，副教授。

收稿日期：2015-03-16

doi:10.3969/j.issn.1671-0436.2015.03.015