变体飞行器的切换LPV控制

何墉, 章卫国, 王敏文, 史静平,

变体飞行器的切换LPV控制

何墉1,2, 章卫国1, 王敏文3, 史静平1,3

摘要：运用切换线性变参数(linear parameter varying, LPV)的控制方法解决变体飞行器在不同机翼构型有不同的控制目标问题。首先根据变体飞行器的任务需求把后掠角变化范围分成不同的区域,针对不同的变化区域分别设计相应的LPV控制器，采用参数依赖公共Lyapunov函数方法实现在变形机构允许的范围内以尽可能快的变体速度实现变体过程。仿真结果表明用所用方法设计的控制器具有良好的响应特性，可实现对指令信号的良好跟踪。

关键词：变体飞行器；切换LPV系统；参数依赖公共Lyapunov函数

传统飞行器飞行模式单一，只能执行特定的飞行任务。随着国防建设的需要和科学技术的不断进步，人们希望拥有一种飞行器能够根据飞行环境和飞行任务的变化而改变外形，始终以最优的飞行状态在变化较大的飞行环境中完成多种飞行任务[1]。常见的变形形式包括改变机翼后掠角、机翼折叠和机翼伸缩等形式。作为一种新概念飞行器，变体飞行器有望成为现代高性能飞行器实现突破发展的源泉，具有重要的研究价值和广阔的应用前景[2]。

变体飞行器的变体过程主要是通过改变机翼的气动外形来实现。机翼形状的改变使得飞行器本体参数如翼面面积、重心位置都随着翼型的改变而改变，由此产生的气动力和动量矩(积)的大小和方向随之发生变化[3]。变体过程中气动力与力矩都会随着飞行器的构型而变化，使得模型具有较强的时变性和不确定性，飞行稳定性会受到较大影响，为了满足飞行品质要求，所设计的飞行控制系统需要确保变体过程中的飞行稳定性[4]。同时对于变体飞行器而言不同的飞行模式有不同的性能指标要求，如巡航飞行时要求变体飞行器有较大的升阻比；而快速撤离战区时则希望飞行器以最小的飞行阻力构型进入工作区域；因此，很难用一种控制器来满足变体飞行器在不同构型下的性能指标。

针对上述问题本文用切换LPV(linear parameter varying,LPV)的方法为变体飞行器的控制问题提供了一种解决方案。LPV系统是一类特殊的线性系统，其状态空间矩阵是以某些时变参数向量为自变量的函数[5-6]。从控制的角度看，系统参数的变化导致其动态特性在工作点附近发生性变化，而LPV控制技术能够处理参数变化及模型本身描述不精确等问题，从而改善系统的动态特性[7]。由于LPV系统本身的特点，使得其在工程实际中应用广泛[8]。对于LPV系统的处理，现有的方法大多是将LPV系统转化为多胞系统来处理[9-10]，这种方法虽然从一定程度上能够实现对LPV系统的近似，但若权系数选择不当会引起多胞系统和实际LPV系统之间的误差过大。文献[11-12]用参数相关Lyapunov函数的方法绕开了用多胞系统对LPV系统的近似，文献[12]基于平均驻留时间的方法考虑了参数大范围变化的一类LPV系统并取得了良好的控制效果，但是用平均驻留时间方法处理切换系统使得切换频率受到限制，若将该方法用于处理变体飞行器变体过程中的稳定性问题时，势必影响其变体速度，据此本文用参数依赖公共Lyapunov函数方法实现变体飞行器在不同控制器间切换时的稳定性和快速性问题。

1变体飞行器的切换LPV建模

基于如图1所示的某型变后掠翼无人机进行研究，机翼后掠角χ的变化范围为15°～16°，平均气动弦长，展长和机翼面积等参数随着后掠角的变化而变化，因此易知该无人机的气动参数都是后掠角的函数，这里给出该变体飞行器的纵向短周期非线性动力学模型：

图1　变后掠翼飞行器

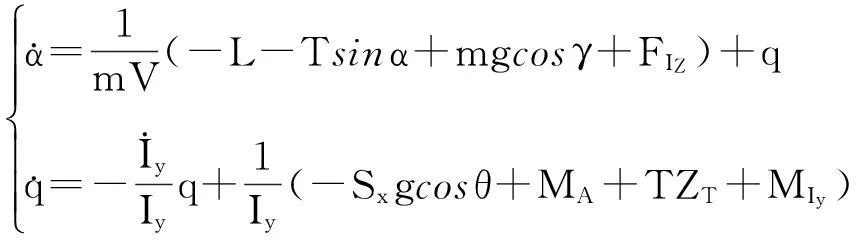
(1)

式中，γ为航迹角,α为迎角,q为俯仰角速度,θ为俯仰角,m为飞机质量,g为重力加速度,V为飞行速度,Iy为飞机绕机体y轴的转动惯量,T为推力,与机体轴x轴方向平行,ZT为动力位置,L和MA分别为升力和由空气动力产生的俯仰力矩,其表达式为

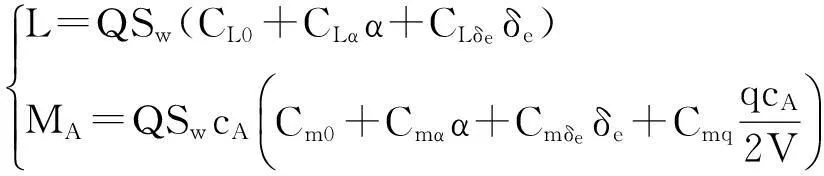
(2)

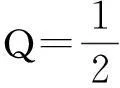
(3)

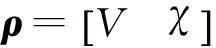
(5)式中，σ(t)是控制子系统切换序列的切换信号,在本文中其值由参数向量ρ(t)决定,这样整个切换LPV系统可以表述为

(6)

2切换LPV控制器设计

考虑如下形式的切换LPV系统模型[14-15]：

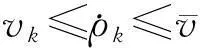
(8)式中，xk∈Rnk,nk=n为控制器的状态。当参数变化到某个区间后使得相应的控制器被激活,所以在每个参数子区域pi内,闭环系统描述为:

引理1(投影引理)设P、Q和H是给定的适当维数的矩阵且H是对称的,NP和NQ分别为由核空间Ker(P)和Ker(Q)的任意一组基向量作为列向量构成的矩阵,那么存在一个矩阵X使得H+PTXTQ+QTXP<0

对于被控对象为(9)的切换LPV系统,基于公共Lyapunov函数的有界实引理描述如下:

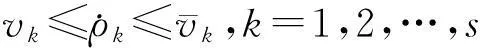
定理考虑开环切换LPV系统(7),参数区域P和其子区域{pi}i∈ZN,如果对于参数区域的每个子区域都存在正定矩阵R(ρ)、S(ρ)和正实数γ使得对于任意pi⊂P都有下列不等式成立

(12)

(13)

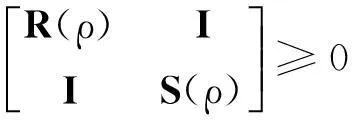
(14)式中

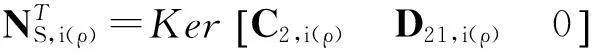
证明:对于任意一个参数子区域pi内的闭环系统,都有如下关系式成立:

(15)式中

这样,经代数运算后(11)式可以等价描述为

(16)式中

*表示矩阵对应块的转置矩阵。

而由投影引理可知(16)式可以等价地写成如下形式:

(17)

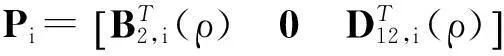
由PXcl,i和Pi的代数关系易得

这样,(17)式可以写为

(19)式中

根据系统和控制器的维数把参数相关Lyapunov函数矩阵进行分割,则Lyapunov函数矩阵及其逆矩阵可以表示为如下形式:

式中，“?”表示对矩阵中对应的元素不关注。经过代数运算后,(19)式等价于(12)式,(18)式等价于(13)式,由引理2易知满足不等式约束的R(ρ)和S(ρ)构成的矩阵Xcl(ρ),由此保证了闭环系统在整个参数区域P二次稳定且H∞性能指标满足‖z‖2<γ‖ω‖2。

通过选取矩阵M(ρ)=R(ρ),N(ρ)=R-1(ρ)-S(ρ),则

用文献[11]中的方法,先定义如下中间变量:

则切换LPV控制器增益矩阵分别为:

(20)

(21)

(22)

(23)

Remark若系统(7)不存在控制输入和量测输出,则系统模型中对应的状态矩阵中B2,i(ρ)=0,C2,i(ρ)=0,D12,i(ρ)=0,D21,i(ρ)=0,此时NR,i(ρ)和NS,i(ρ)退化为单位阵,在这种条件下定理条件中的三个不等式变为

(24)

(25)

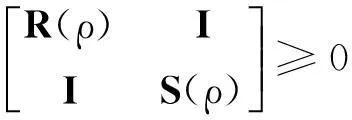
(26)

由矩阵运算的性质易知,如果R(ρ)>0满足矩阵不等式(24),则S(ρ)=R-1(ρ)>0满足矩阵不等式(25)。因此不等式条件(24)～(26)等价于存在参数相关正定对称矩阵R(ρ)使(24)式成立;或存在参数相关正定对称矩阵S(ρ)使(26)式成立。同时,从以上的分析可以看到NR,i(ρ)和NS,i(ρ)分别反映了系统的控制输入不能影响的部分和系统的量测输出不能放映的部分。

3仿真验证及分析

本节基于前文给出的变体飞行器切换LPV模型进行仿真研究。先从待设计的区域内选择一些点作为参考点,围绕着这些点进行配平并由局部线性化的方法从飞行器的非线性方程得到线性小扰动方程。变体飞行器切换LPV系统的结构如图2所示,其中P(ρ)是在多个点线性化的飞行器纵向短周期动态模型,把它的2个状态迎角α和俯仰角速率q作为输出,跟踪的理想模型为

其输出αideal和实际迎角输出α的差α-αideal作为跟踪误差,通过权值函数惩罚跟踪误差。外部输入包括二维传感器噪声n和迎角指令信号acmd。被控输出为开环加权误差信号为αp和za,这样跟踪问题就转化为外部输入和被控输出之间的H∞控制问题。

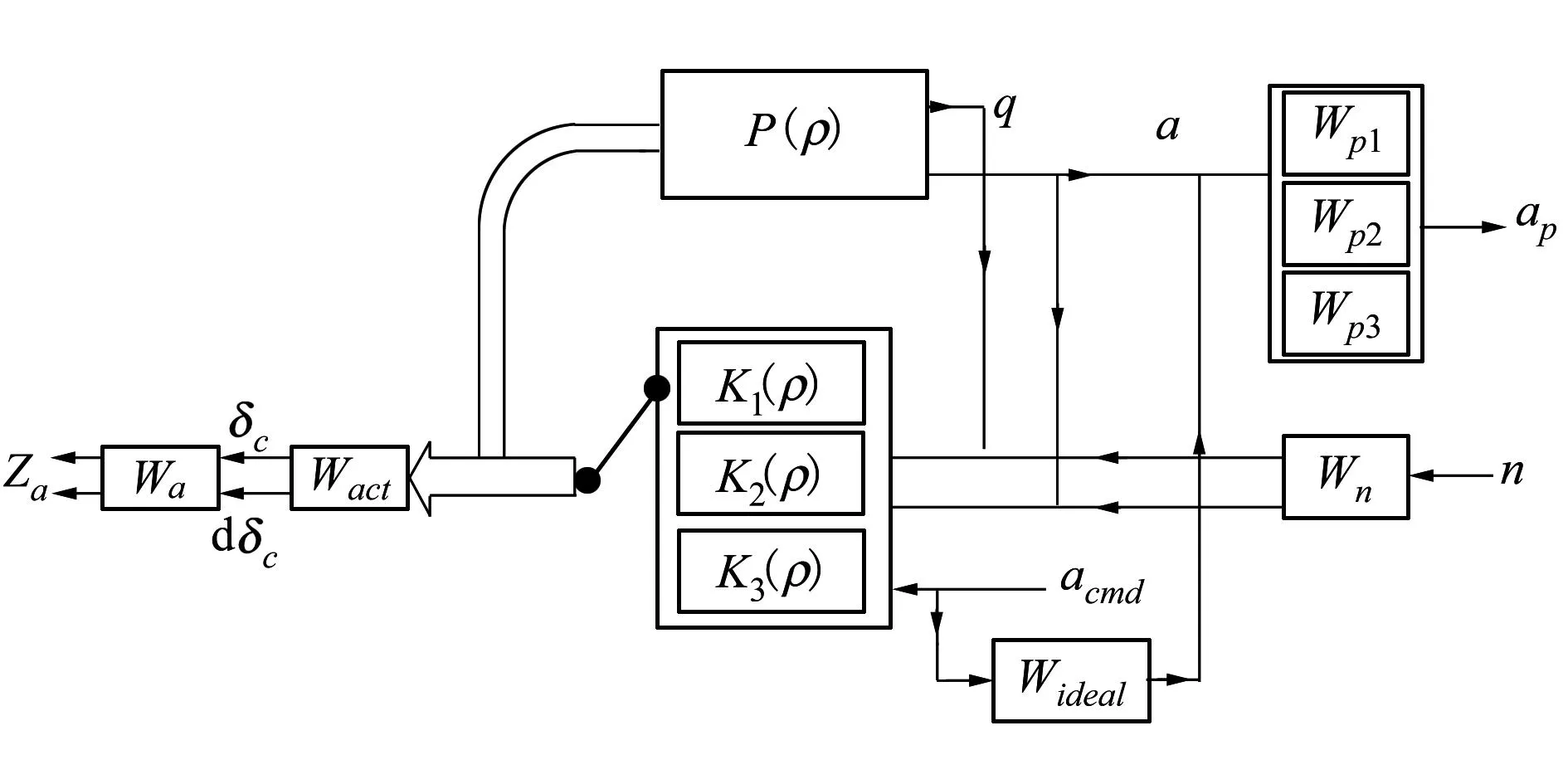
图2　变体飞行器切换LPV系统的结构图

由于在不同的后掠角变化范围内有不同的控制目标,在后掠角比较小的时候我们希望飞行器对指令信号有快速而准确的响应;而在后掠角比较大时,对飞行器的飞行品质要求不是很苛刻,主要强调飞行器的稳定性。基于此我们把后掠角的变化范围分为3个区域:[15°～30°]、[30°～45°]和[45°～60°],K1(ρ)、K2(ρ)和K3(ρ)分别是用本文所用方法设计的不同后掠角变化区域的3个LPV控制器。对3个区域分别选择3个权值函数

来体现设计要求,其中下角标1、2和3分别对应于后掠角的3个变化区域,3个权值函数体体现在不同的后掠角区域所对应的设计要求。3个区域跟踪的稳态误差分别为1.25%、1.11%和1%,系统带宽在3个子区域中也逐渐增加,因此不论从稳态误差还是系统带宽,都和我们的控制目标相一致[11]。作动器动态模型Wact为

控制输入的惩罚函数Wu为Wu=diag(0.1,0.2)。

设待求解的参数依赖公共Lyapunov函数矩阵是具有如下形式的参数仿射型矩阵

式中，ρ=χ为变体飞行器的后掠角,矩阵Ri和Si,(i=0,1)是待优化求解的矩阵。

下面分别给出了变体飞行器用本文所用的公共Lyapunov函数方法和文献[12]中所用的平均驻留时间方法对H∞性能指标的比较。

表1给出了参数依赖多Lyapunov函数方法和公共Lyapunov函数方法所对应的H∞性能指标的比较。由表可知,用文献[12]中平均驻留时间方法在不同的子区域设计控制器得到的H∞性能指标不同。当后掠角在15°～60°范围内变化时用本文所用的方法得到的H∞性能指标为13.226 2,该指标大于用平均驻留时间方法得到的最大H∞性能指标8.955 3,但用本文所用的方法不用考虑单个子系统的激活时间,这样就放松了对飞行器后掠角变化速度的限制,可以在变形机构允许的范围内尽可能快地完成变形动作,这种需求在某些飞行任务中(如迅速撤离战区)是必要的。

表1　2种方法的H∞性能指标对比

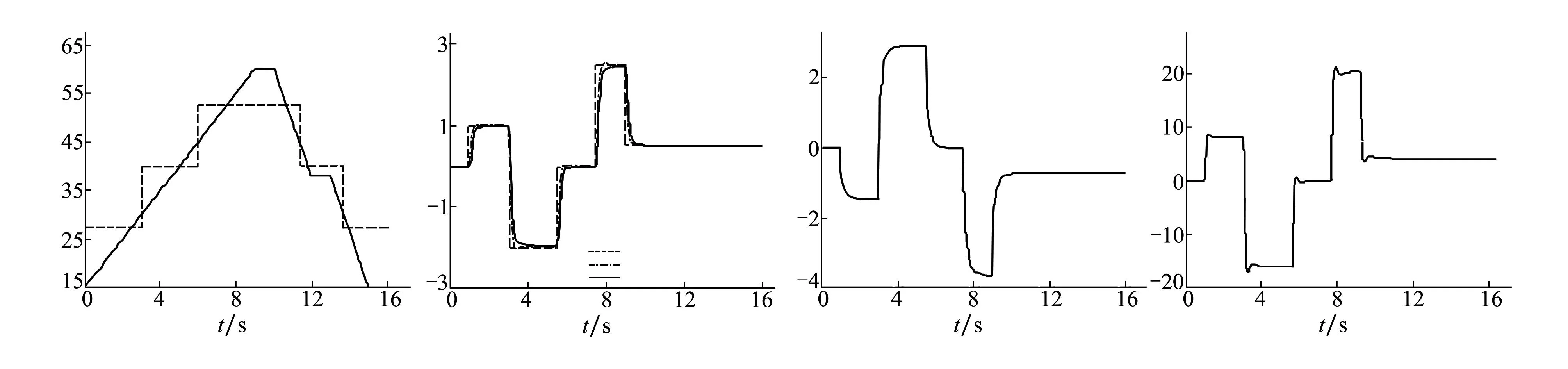
图3　后掠角信号及切换信号 图4　变体飞行器的迎角响应曲线　　图5　升降舵偏角图6　俯仰角速率

图3和图4分别给出了变体飞行器以不同的变体速度实现变体的过程中对迎角指令信号的跟踪效果图。图3中的后掠角先以5°/s的变体速度从0°构型变形到45°构型,保持45°构型模式运行1 s后又以10°/s的变体速度从45°构型变化到25°构型,运行1 s后又以12.5°/s的变体速度变化到0°构型并保持该构型模式。随着后掠角的变化激活相应的控制器,相应的切换信号如图3中的虚线。图4给出了变体飞行器变体过程中对迎角指令信号的跟踪曲线。从仿真的结果看在各种变体速度下飞行器都能实现对指令信号的跟踪。图5和图6给出了变体飞行器在给定的后掠角变化曲线和迎角指令信号下的升降舵偏角和俯仰角速率响应曲线。

4结论

本文用切换LPV控制的方法解决变体飞行器变体过程中的稳定性问题，在设计过程中结合变体飞行器在不同的机翼构型有不同的控制目标，根据不同的控制目标分别设计LPV控制器。采用本方案的最大优点是在变体过程中可以不去考虑变体速度的限制，可在变形机构允许的范围内以尽可能快的变体速度完成变形过程。仿真结果表明变体飞行器以不同的后掠角变化速度变形时对指令信号都有较好的跟踪效果。

参考文献：

[1]陆宇平，何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10): 1906-1911

Lu Yuping, He Zhen. A Survey of Morphing Aircraft Control Systems[J]. Acta Aeronatuca et Astronautica Sinica, 2009, 30(10): 1906-1911 (in Chinese)

[2]王青，王通，后德龙，等. 基于速度线性化的变体飞行器鲁棒LPV控制[J]. 系统工程与电子技术, 2014, 36(6): 1130-1136

Wang Qing, Wang Tong, Hou Delong, et al. Robust LPV Control for Morphing Vehicle via Velocity-Based Linearization[J]. Systems Engineering and Electronics, 2014, 36(6):1130-1136 (in Chinese)

[3]乐挺，王立新，艾俊强. Z型翼变体飞机的纵向多体动力学特性[J]. 航空学报, 2010,31(4): 679-686

Yue Ting, Wang Lixin, Ai Junqiang. Longitudinal Multibody Dynamic Characteritics of Z-Wing Morphing Aircraft[J]. Acta Aeronatuca et Astronautica Sinica, 2010, 31(4): 679-686 (in Chinese)

[4]陈伟，卢京潮，王晓光，等. 基于backstepping/RHO的变体飞机控制器设计[J]. 北京航空航天大学学报, 2014, 40(8): 1160-1165

Chen Wei, Lu Jingchao, Wang Xiaoguang, et al. Design of a Controller for Morphing Aircraft Based on Backstepping/RHO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(8):1160-1165 (in Chinese)

[5]崔平. LPV系统的鲁棒故障估计与主动容错控制[D]. 上海：上海交通大学, 2008

Cui Ping. Robust Fault Estimation and Active Fault Tolerant Control for Linear Parameter Varying Systems[D]. Shanghai: Shanghai Jiao Tong University, 2008 (in Chinese)

[6]Petres Z A. Polytopic Decomposition of Linear Parameter-Varying Models by Tensor-Product Model Transformation[D]. Budapest University of Technology and Economics, 2006

[7]吴定会，李意扬，纪志成. 风力机的线性变参数主动容错控制[J]. 控制理论与应用, 2014,31(4): 425-430

Wu Dinghui, Li Yiyang, Ji Zhicheng. Active Fault-Tolerant Linear-Parameter-Varying Control of Wind Turbines[J]. Control Theory & Applications, 2014, 31(4): 425-430 (in Chinese)

[8]Lu Q, Zhang L, Shi P, et al. Control Design for a Hypersonic Aircraft Using a Switched Linear Parameter-Varying System Approach[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2013, 227(1): 85-95

[9]Yue T, Wang L, Ai J. Longitudinal Linear Parameter Varying Modeling and Simulation of Morphing Aircraft[J]. Journal of Aircraft, 2013, 50(6): 1673-1681

[10] 张增辉，杨凌宇，申功璋. 高超声速飞行器大包线切换LPV控制方法[J]. 航空学报, 2012(9): 1706-1716

Zhang Zenghui, Yang Lingyu, Shen Gongzhang. Switching LPV Control Method in Wide Flight Envelop for Hypersonic Vehicle[J]. Acta Aeronautica et Astronautic Sinica, 2012(9): 1706-1716 (in Chinese)

[11] Bei L, Fen W, Sungwan K. Switching LPV Control of an F-16 Aircraft via Controller State Reset[J]. IEEE Trans on Control Systems Technology, 2006, 14(2): 267-277

[12] Lu B, Wu F. Switching LPV Control Designs Using Multiple Parameter-Dependent Lyapunov Functions[J]. Automatica, 2004, 40(11): 1973-1980

[13] Lu Q, Zhang L, Shi P, et al. Control Design for a Hypersonic Aircraft Using a Switched Linear Parameter-Varying System Approach[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2013, 227(1): 85-95

[14] He X, Dimirovski G M, Dimirovski G M, et al. Control of Switched LPV Systems Using Common Lyapunov Function Method and an F-16 Aircraft Application[C]//2010 IEEE International Conference on Systems Man and Cybernetics, 2010

[15] Lu B, Wu F. Switching LPV Control Designs Using Multiple Parameter-Dependent Lyapunov Functions[J]. Automatica, 2004, 40(11): 1973-1980

[16] Apkarian P, Gahinet P, Becker G. Self-ScheduledH∞ Control of Linear Parameter-Varying Systems: a Design Example[J]. Automatica, 1995, 31(9): 1251-1261

Switching LPV Control for Morphing Aircraft

He Yong1,2, Zhang Weiguo1, Wang Minwen3, Shi Jingping1,3

Abstract:A switching linear parameter varying (LPV) system was applied to deal with multiple design objectives during the flight of morphing aircraft. A group of LPV controllers are then designed based on common parameter-dependent Lyapunov function and each of them is suitable for a specific subregion of the sweep angle; the process can be accomplished quickly within the permission of the morphing mechanism under the common parameter-dependent Lyapunov function scheme. The simulation results show that the controller designed in this paper can make the morphing aircraft have good response characteristics and tracking of command signal.

Key words:morphing aircraft; switching LPV system; common parameter-dependent Lyapunov function

中图分类号：V241.62

文献标志码：A

文章编号:1000-2758(2015)05-0781-07

作者简介：何墉(1980—)，西北工业大学博士生，主要从事飞行控制方法的研究。

基金项目：国家自然科学基金(61374032)与航空科学基金(20140753012)资助

收稿日期：2015-03-02