梯度增强的Kriging模型与Kriging模型在优化设计中的比较研究
刘俊, 宋文萍, 韩忠华, 王乐
(西北工业大学 翼型叶栅空气动力学国家级重点实验室, 陕西 西安 710072)
梯度增强的Kriging模型与Kriging模型在优化设计中的比较研究
刘俊, 宋文萍, 韩忠华, 王乐
(西北工业大学 翼型叶栅空气动力学国家级重点实验室, 陕西 西安710072)
摘要:在许多工程优化设计问题中,由于需要采用费时的数值模拟方法获得目标函数和约束函数值,出现了优化时间过长、优化难度大的问题。为了提高设计效率,缩短优化设计周期,代理模型方法受到人们的欢迎。近些年来,为了进一步提高设计效率,人们在传统代理模型基础上又发展了一些更高效、预测精度更高的新型代理模型,如变可信度模型、梯度增强的代理模型等。为了研究新型代理模型在优化设计中的优化效率和优化效果,首先结合代理模型、多点加点准则及多种传统优化算法,发展了一套适用于代理模型、梯度增强的代理模型的通用优化算法框架,基于该框架,采用典型的数值算例对当前应用较为广泛的Kriging模型和近些年来发展的梯度增强的Kriging模型进行了对比研究。结果显示,在假定目标函数的梯度与目标函数计算量相同的情况下,采用梯度增强的Kriging模型得到的优化结果在绝大多数情况下都优于采用Kriging模型得到的结果。最后,应用翼型设计算例对两种代理模型进行了对比,其中目标函数的梯度采用与目标函数本身计算量基本一致的Adjoint方法获得;结果显示,梯度增强的Kriging模型表现优于Kriging模型。
关键词:优化设计;代理模型;Kriging模型;梯度增强的Kriging模型;气动优化设计
在工程优化设计领域,目标函数的获得往往十分耗时,发展高效的优化方法(即减少目标函数的计算次数)是缩短设计周期的关键。此外,为了提高设计效果,优化方法应尽可能地具有好的全局性,即应尽可能地找到全局最优解。
基于代理模型的优化方法被认为是一类能够实现全局优化的高效优化方法。Kriging模型具有较好的预测非线性、多峰值的能力,且能预测出未知点的误差,因而成为最受欢迎的代理模型之一,并被越来越多地应用于多学科优化设计中[1-3]。尽管如此,Kriging模型的效率和精度有时仍然不能满足工程实际的需求,这是由于在很多实际问题中,建立一个具有合理精度的近似模型仍然需要大量的高精度数值模拟,而这一问题将随着设计变量的个数和范围的增加变得更加突出。为此,近些年来,人们正寻求比传统代理模型更为高效的新型代理模型。
提高代理模型效率的一种方法是使用大量低可信度样本数据来辅助高可信度样本数据来建立一种用于预测高可信度分析程序输出结果的变可信度模型[4-7],如Cokriging模型。该方法的思想是在设计空间内同时采用高可信度分析程序(如Navier-Stokes方程程序)和低可信度程序(如Euler方程程序)进行抽样,通过大量的低可信度样本数据获得设计空间内响应值的全局趋势,通过少量高可信度样本数据来校正预测值。另一种提高Kriging模型效率的方法是在Kriging模型中引入梯度信息,即在建立代理模型时不仅利用样本点处的函数值,同时利用样本点处的梯度值。引入梯度的Kriging模型被称为梯度增强的Kriging模型(gradient-enhanced Kriging,GEK)。Liu等[8]提出了一种间接GEK模型。Chung等[9]提出了一种直接GEK模型。Laurenceau等[10]比较了Kriging、直接GEK、间接GEK模型在气动问题中的预测精度,发现在相同样本点数下2种GEK的精度都高于Kriging模型。Han等[1]发展了一种更一般化的GEK模型, 允许梯度信息在任意位置引入,且允许在某些样本点处不使用梯度信息。
目前,对于Kriging模型及基于该模型的优化方法已得到大量研究,对于GEK模型本身的研究也不少见[9-12],而鲜见对GEK模型和Kriging模型在应用于优化设计时的优化效率和优化效果的比较仔细的对比研究。为了探讨GEK模型在优化设计中的效率及效果,本文首先在Han等[11]发展的GEK模型基础上,结合多种加点准则[13]及多种传统优化算法,发展了一套基于代理模型的高效优化设计框架;其次,在统一的优化框架下,采用典型数值算例将GEK模型和Kriging模型进行了对比研究,最后采用工程中的气动设计问题将二者进行了对比。结果显示,对于大多数问题,使用GEK时收敛更快且优化结果更好。
1Kriging模型/梯度增强的Kriging模型
参考文献对于Kriging模型的详细介绍,本文不再赘述,见相关[1,14-15]。GEK模型是在Kriging模型基础上发展起来的,其思想、原理和建模方法与Kriging模型基本一致,只是在模型中不仅利用了样本点处的函数值,还利用了样本点处的梯度值。下面介绍本文所采用的由Han等[11]发展的一种直接GEK模型。
首先,在Kriging模型中,对于一个m维问题,假设对目标函数(或约束函数)y抽样获得n个函数值,抽样位置及相应的响应值可写成
(1)
对于GEK,将上述样本数据的响应值列向量加以拓展,把样本点处的梯度信息以偏导数的形式加入到响应值中。于是得到含梯度信息的样本及响应值矩阵:
(2)
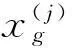
1.1GEK预测值与均方误差
GEK模型对未知函数的预测值定义为所有抽样函数值和所有抽样偏导数值的加权,即
(3)
式中,w(i)代表第i个函数值的加权系数,λ(j)代表第j个偏导数信息的加权系数。与Kriging模型类似,引入静态随机过程假设:
(4)
式中,β0是未知的常数,Z(·)为均值为0的静态随机过程,且协方差满足关系式
cov[Z(x(i)),Z(x(j))]=σ2R(x(i),x(j)),
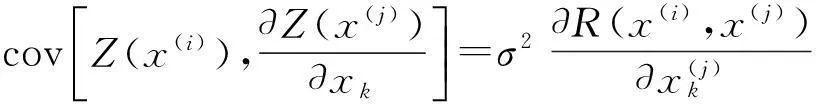
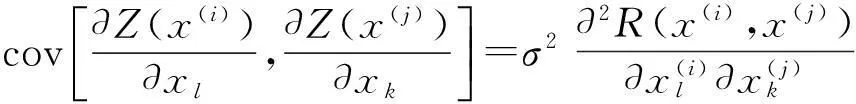
(5)
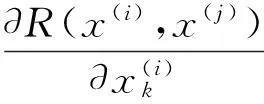
与Kriging模型推导过程类似,可得到GEK模型的预测值:
(6)
式中,R为样本点相关矩阵,r为样本点与未知点x的相关向量:
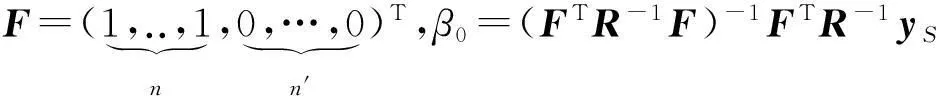
均方误差MSE由下式计算:
(7)
1.2相关函数模型
相关矩阵R和相关向量r的建立需要计算相关函数及其一阶导数、二阶导数值。此处考虑以下形式的相关模型:
(8)
本文采用与文献[11]类似的3次样条相关函数:
(9)
1.3模型参数的获得
由(8)式可知,GEK模型中存在超参数θ,与Kriging模型相同,θ值采用最大似然估计法求解下列优化问题获得:
(10)
2多点加点准则及其约束处理
基于代理模型的优化方法的一个关键技术是加点准则。由于建立一个较精确的全局近似模型需要大量的样本点,特别是设计变量较多时。因此,为了减少总的样本点数,首先使用较少的样本点建立初始代理模型,再寻找一定准则下的最优点并将其作为新的样本点来更新代理模型重新优化。加点准则的使用直接决定了优化的成败及优化效率。本文发展一种多点加点准则:同时采用局部收敛性好的目标函数最小值准则和全局收敛性好的EI最大准则,并分别将其推广到含约束的形式。
2.1目标函数值最小准则及其约束处理
该准则认为代理模型足够精确,直接寻找代理模型上目标函数的最小值,即建立代理模型后,求解下列子优化问题:
(11)
式中,NG是约束个数。本文使用遗传算法(GA)和梯度优化相结合的方法求解最小化问题。
该准则没有考虑模型的误差,新加的样本点主要集中在当前真实最优解附近,因而它是一种局部加点准则。本文称之为minimizingtheconstrainedprediction, 简称CMP。
2.2EI最大值准则及其约束处理(CEI)
设样本集中的最优目标函数值为ymin,在x处目标函数相对的改进量为I=ymin-Y(x)>0,于是I的期望值可由下式计算:
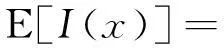
(12)
式中,φ表示标准正态分布概率密度函数,Φ表示标准正态分布累积函数。

(13)
满足约束的EI值(CEI)如下:

(14)
若存在多个约束,则将(12)式中乘以每一个约束函数满足约束的概率。
该准则以当前真实最优解为参照,同时考虑了代理模型的误差,因而是一种全局加点准则。
上述2种加点准则的结合兼顾了优化的局部收敛性和全局收敛性,因而可以更好地适用局部优化问题和全局优化问题。
3基于代理模型的优化设计方法
本文结合代理模型、试验设计方法(本文采用LHS)、多点加点准则、遗传算法、梯度优化算法等发展了1套基于GEK模型的优化设计方法。该方法的流程如下:
1) 使用试验设计在设计空间内生成一些初始样本点。
2) 调用真实分析模型,获得每个样本点的真实目标函数值和约束函数,对于GEK模型,还需计算二者的梯度值。
3) 针对目标函数及每一个约束函数,分别建立目标函数和约束函数的代理模型。
4) 分别使用CEI和CMP进行子优化,获得代理模型上的2个最优解。
5) 检查2个新的最优点是否重合或与已有的样本点出现重合,若重合,剔除新出现的重叠点。
6) 调用真实函数校验两种加点准则所得的最优点的真实目标函数值和约束函数,对于GEK模型,还需计算二者的梯度。
7) 检验优化是否达到终止标准,若是,停止优化,否则将上步中所得最优点作为新样本点加入样本点集,回到步骤3)。
4算例测试
在本文优化算例中,为了与Kriging模型进行对比,假设计算1次目标函数的梯度所需的计算量等同于1次目标函数的计算量(类似在气动优化设计中,若使用Adjoint方法[12]计算梯度,其计算量大致等于1次流场求解的计算量。由于初始样本点的生成具有随机性,且在子优化过程中使用了具有随机性的遗传算法,因此,本文基于代理模型的优化算法也会存在随机性。因此本文对所有算例重复优化30次来进行研究。
4.1无约束算例(局部优化)
该算例是求解Rosenbrock函数的最小值。优化模型如下:
minimize:f(x)=
(15)
其真实最优解为x*=(1.0,…,1.0),f(x*)=0。图1给出了Rosenbrock函数的云图,图中的“+”为最优点。

图1 Rosenbrock函数云图
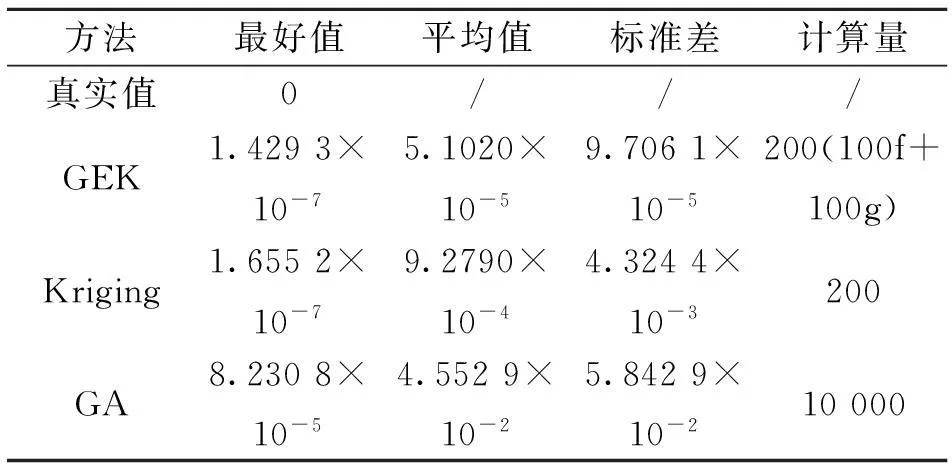
分别使用Kriging模型和GEK模型进行优化,在优化过程中,使用LHS方法生成4个初始样本点。使用GEK模型进行优化时,最大样本点数取100,加上100次梯度所需的计算量,总计200个计算量。在使用Kriging模型进行优化时,最大样本点数取200。图2给出了使用Kriging模型和GEK模型运行30次得到的平均收敛曲线的比较。可以看出,在相同的样本点数情况下,使用GEK模型优化的结果明显优于Kriging模型优化的结果。然而,计算梯度需要额外的计算量,在相同计算量情况下,使用GEK模型优化的结果好于Kriging模型优化的结果。表1给出了使用GEK模型、Kriging模型优化结果的比较。作为参照,表中还给出了直接使用GA优化得到的结果。从表1还可以看出使用2种代理模型方法的优化结果都明显优于GA所得的结果,尽管GA调用了10 000次目标函数。(表中“计算量”一列中“f”表示真实目标函数计算,“g”表示真实目标函数的梯度计算作为参照。)

图2 使用Kriging和GEK优化Rosenbrock函数的 目标函数平均收敛曲线对比
方法最好值平均值标准差计算量真实值0///GEK1.4293×10-75.1020×10-59.7061×10-5200(100f+100g)Kriging1.6552×10-79.2790×10-44.3244×10-3200GA8.2308×10-54.5529×10-25.8429×10-210000
4.2无约束算例(全局优化)
本算例是一个全局优化算例,目标是求解Rastrigin函数的最小值,优化模型如下:
minimize:f(x)=
(16)
函数的真实最优解为x*=(0,…,0),f(x*)=0。图3给出了Rastrigin函数图,可以看出,该函数是一个复杂多极值函数。

图3 Rastrigin函数
使用LHS方法获得10个初始样本点。使用GEK模型进行优化时,最大样本点数取150;使用Kriging模型进行优化时,最大样本点数取300。图4给出了使用Kriging模型和GEK模型运行30次得到的平均收敛曲线。可以看出,基于Kriging模型的优化方法和基于GEK模型的优化方法都表现很好。然而,GEK模型优化的收敛精度要高于Kriging模型优化的收敛精度。表2给出了使用本文GEK方法、基于Kriging模型的优化方法优化结果的比较。该表也反映了图4所显示的结果。作为参考,表中也给出了直接使用GA优化得到的结果。

图4 使用Kriging和GEK优化Rastrigin函数 的目标函数平均收敛曲线对比

方法最好值平均值标准差计算量真实值0///GEK1.5792×10-121.0088×10-101.6978×10-10300(150f+150g)Kriging4.5025×10-112.4409×10-87.9442×10-8300GA03.5527×10-161.9459×10-1530000
4.3约束优化算例
本算例是一个压力容器设计问题。该优化问题的数学模型如下所示:
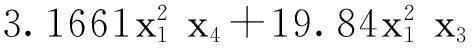
s.t. g1=-x1+0.0193x3≤0
g2=-x2+0.00954x3≤0
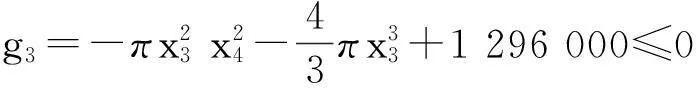
g4=x4-240≤0
0.062 5≤x1,x2≤6.187 5,
10.0≤x3,x4≤200.0
(17)
图5给出了2种代理模型方法重复优化的平均收敛曲线的对比。表3给出了3种方法分别优化30次所得最好最优值、平均最优值、最优值的标准差,以及计算量的比较。与上例类似,GEK模型几乎每次都精确地收敛到相同的值,30次重复优化最优值的平均值和标准差都小于Kriging,这说明GEK模型效果好于Kriging且表现更稳定。该表也给出了直接使用GA优化得到的结果,可以看出,使用基于GEK和Kriging的优化方法所得的优化结果都明显优于GA,而计算量却远小于GA。
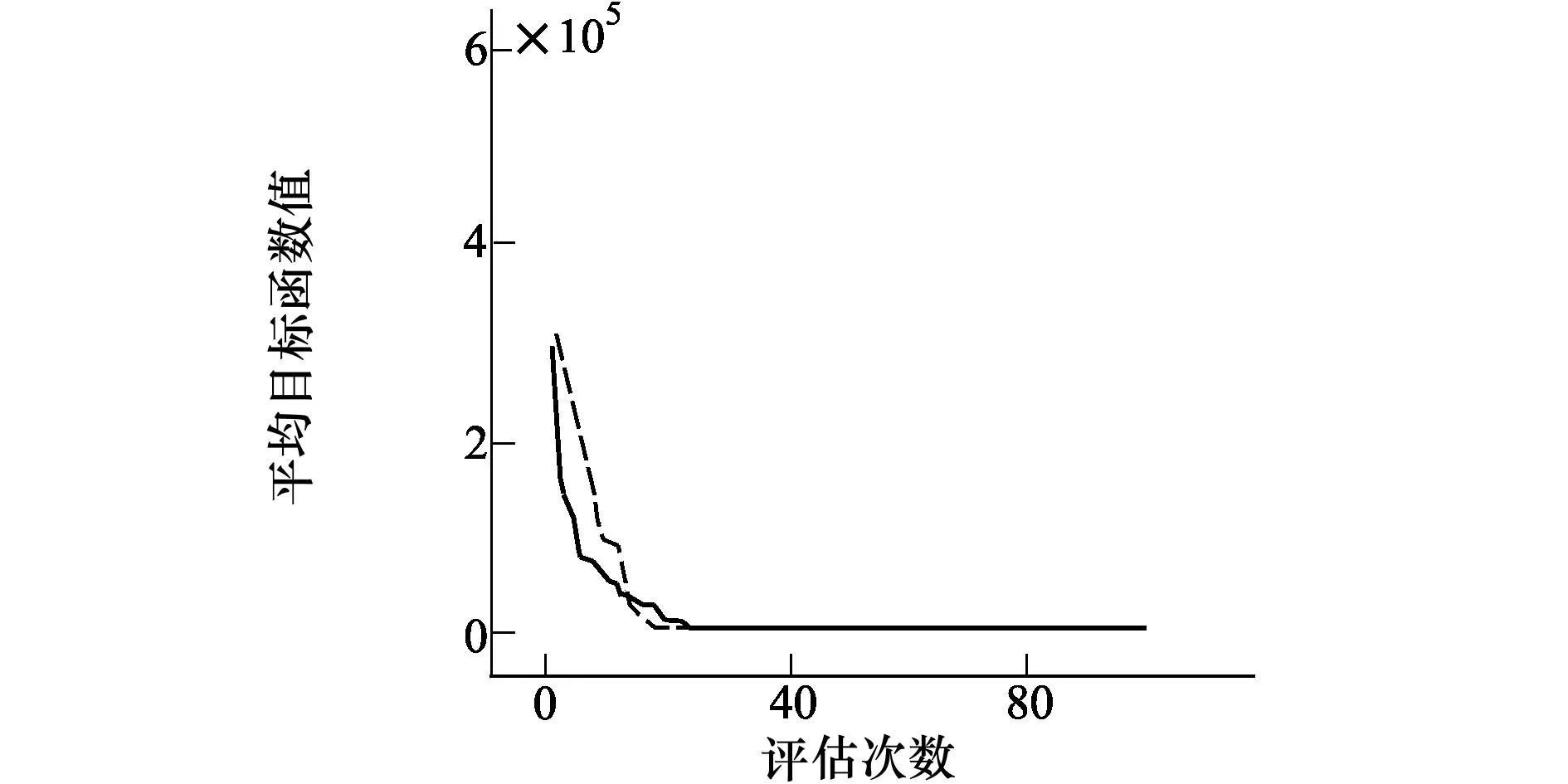
图5 使用Kriging和GEK优化pressure vessel design的 目标函数平均收敛曲线对比
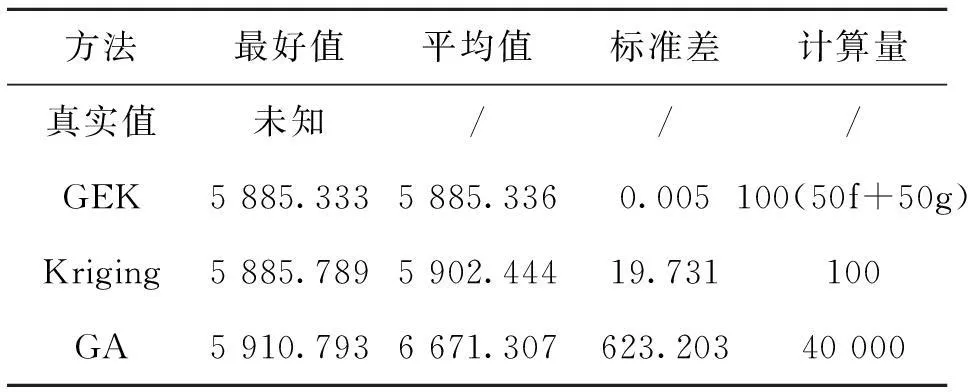
方法最好值平均值标准差计算量真实值未知///GEK5885.3335885.3360.005100(50f+50g)Kriging5885.7895902.44419.731100GA5910.7936671.307623.20340000
4.4翼型设计算例
为了比较2种代理模型应用于工程优化设计的的优化效率和效果,以翼型压力反设计进行测试。
设计状态为Ma=0.73,Re=6.5×105,α=2.0°。首先给定RAE2822翼型在该设计状态的压力分布,以该压力分布作为目标压力分布,将反设计问题转化为优化问题求解,优化问题的数学表达式如下:

(18)
式中,p为计算压力,pd为目标压力,B表示沿物面的积分。
翼型的几何参数化采用“CST”参数化方法[17],18个设计变量。流场求解采用课题组发展的求解器PMNS2D;计算网格采用C型结构化网格。目标函数的梯度使用Adjoint方法计算。因此,通过求解一次RANS方程和一次与之计算量相当的Adjoint方程即可得到目标函数及其梯度值。
分别使用GEK模型、Kriging模型进行翼型的反设计,重复运行30次。作为参考,这里还给出了使用基于Adjoint的梯度优化算法所得的结果,其中梯度优化算法采用BFGS拟牛顿法,初始翼型为NACA0012翼型。图6给出了基于代理模型的优化方法的平均收敛曲线及Adjoint方法收敛曲线的对比。从图6可以看出,使用Kriging时花费300个样本点已基本收敛,而GEK方法仅花费50个样本点(100个计算量)目标函数就已收敛,优化结果也好于使用Kriging模型。

图6 基于GEK方法和Kriging方法的优图7 使用GEK和Kriging模型反 化方法的翼型反设计平均收敛曲线 设计前后翼型的压力分布及 及Adjoint翼型反设计收敛曲线对比 几何形状与目标翼型的对比 (一次Adjoint方程计算等同于 一次流场计算)
图7给出了分别使用GEK、Kriging所得的某次反设计结果对应的翼型几何形状及压力分布与目标翼型几何形状及压力分布的对比。可以看出,使用2种模型反设计所得的翼型的几何形状及压力分布与目标翼型的几何形状及压力分布都吻合得很好,但是仔细比较,GEK表现比Kriging更好,这可在图中圆圈部分可以看出。
5结
在气动设计领域,由于当前已具备高效计算梯度的技术——Adjoint方法,因此,将目标函数与其梯度相结合建立代理模型来进行优化设计,可能有着很大的潜力。为了研究梯度的引入对优化设计的影响,本文首先将Kriging模型、梯度增强的Kriging模型、多点加点准则、多种传统优化算法相结合,发展了一套基于代理模型的高效、通用优化设计框架。其中,本文发展了一种多点加点准则,并将加点准则推广到含约束的形式。再次,基于相同的优化设计框架,对使用梯度增强的Kriging模型和使用Kriging模型的优化结果进行了比较。在假设梯度的计算花费与目标函数的计算花费相同的情况下,对于绝大多数问题,在总的计算量一致的前提下,使用GEK时收敛更快且优化结果更好。此外,还使用工程实际中的翼型压力反设计对Kriging和GEK的效果进行了对比,结果显示,当使用GEK模型时,优化结果和优化效率都高于使用Kriging模型。
[1]Hoyle N, Bressloff N W, Keane A J. Design Optimization of a Two-Dimensional Subsonic Engine Air Intake[J]. AIAA Journal, 2006, 44(11): 2672-2681
[2]Ahmed Mym, Qin N. Surrogate-Based Multi-Objective Aerodynamic Design Optimization of Hypersonic Spiked Bodies[J]. AIAA Journal, 2012, 50(4): 797-810
[3]Yim J, Lee B J, Kim C. Exploiting Multi-Stage Shape Optimization Strategy of Multi-Body Geometries Using Kriging-Based Model and Adjoint Method[J]. Computers & Fluids, 2012, 68: 71-87
[4]Kennedy M C, O′Hagan A. Predicting the Output from a Complex Computer Code When Fast Approximations Are Available[J]. Biometrika, 2000, 87(1): 1-13
[5]Forrester A I J, Soberster A, Keane A J. Multi-Fidelity Optimization via Surrogate Modeling[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 463: 3251-3269
[6]Han Z H, Zimmermann R, Goertz S. An Alternative CoKriging Model for Variable-Fidelity Surrogate Modeling[J]. AIAA Journal, 2012, 50(5): 1205-1210
[7]Han Z H, Goertz S. A Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling[J]. AIAA Journal, 2012, 50(9): 1885-1896
[8]Liu W, Batill S M. Gradient-Enhanced Response Surface Approximations Using Kriging Models[R]. AIAA-2002-5456
[9]Chung H S, Alonso J J. Using Gradients to Construct Cokriging Approximation Models for High-Dimensional Design Optimization Problems[R]. AIAA-2002-0317
[10] Laurenceau J, Sagaut P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and CoKriging[J]. AIAA Journal, 2008, 46(2): 498-507
[11] Han Z H, Goertz S, Zimmermann R. Improving Variable-Fidelity Surrogate Modeling via Gradient-Enhanced Kriging and a Generalized Hybrid Bridge Function[J]. Aerospace Science and Technology, 2013, 25(1): 177-189
[12] Jameson A. Aerodynamic Design via Control Theory[J]. Journal of Scientific Computation, 1988, 3(3): 233-260
[13] Jones D R. A Taxonomy of Global Optimization Methods Based on Response Surfaces[J]. Journal of Global Optimization, 2001, 21: 345-383
[14] Han Z H, Zhang K S, Song W P, et al. Optimization of Active Flow Control Over an Airfoil Using a Surrogate-Management Framework[J]. Journal of Aircraft, 2010, 47(2): 603-612
[15] Han Z H, Zhang K S, Liu J, et al. Surrogate-Based Aerodynamic Shape Optimization with Application to Wind Turbine Airfoils[R]. AIAA-2013-1108
[16] 许瑞飞,宋文萍, 韩忠华. 改进Kriging模型在翼型气动优化设计中的应用研究[J]. 西北工业大学学报, 2010,28(4):503-510
Xu R F, Song W P, Han Z H. Application of Improved Kriging-Model-Based Optimization Method in Airfoil Aerodynamic Design[J]. Journal of Northwestern Polytechnical University, 2010, 28(4): 503-510 (in Chinese)
[17] 卜月鹏,宋文萍,韩忠华,许建华. 基于CST参数化方法的翼型气动优化设计[J]. 西北工业大学学报,2013,31(5): 829-836
Bu Yuepeng, Song Wenping, Han Zhonghua, et al. Aerodynamic Optimization Design of Airfoil Based on CST Parameterization Method[J]. Journal of Northwestern Polytechnical University, 2013, 31(5): 829-836(in Chinses)
Comparative Study of GEK (Gradient-Enhanced Kriging) and
Kriging When Applied to Design Optimization
Liu Jun, Song Wenping, Han Zhonghua, Wang Le
US News and World Report把北大、清华、复旦
列入2016年世界高校最强的前96名
中国日报Thursday,Cotober 8th,2015刊载了US News and World Report 2014年开始列出world′s top 750 universities overall的名次。2016年世界最强高校的前10名,8个在美国(第1名Harvard,第2名MIT,第3名UC Berkeley,第4名Stanford,第7名CIT,第8名UCLA,第9名Columbia,第10名Chicago)2个在英国(第5名Oxford,第6名Cambridge)。
中国三校列入2016年世界最强高校的前96名:北京大学41名,清华大学59名,复旦大学96名。
在工科科研方面2016年rankings把清华大学列为世界最强高校。
胡沛泉
2015年10月

Abstract:In many engineering optimization design problems, the objective function (s) as well as the constraint function (s) are really computationally expensive. To reduce the computational time and shorten the design process, surrogate models are often used. In recent years, to further improve the design efficiency, a variety of new surrogate models are developed as extensions from the traditional models and verified to have higher efficiency for prediction, such as the variable-fidelity models and gradient-enhanced models. To investigate the design optimization efficiency when these new surrogate models are used, a universal surrogate-based optimization framework, which combines the surrogate models, multi sample point infill criteria, and multi-type traditional optimization algorithms, is developed first. Then, several typical analytical optimization problems are employed to compare the optimization efficiency when the widely used Kriging and a newly developed GEK are used respectively. The results and their analysis show preliminarily that, for most cases, GEK get better optimal solution with the same computational expense. Finally, an engineering problem, the airfoil inverse design is introduced for comparison; the gradients of the objective functions used to construct the GEK are obtained by the efficient adjoint method. The results and their analysis also show preliminarily that, when using the GEK, not only the efficiency, but also the optimal solution can be improved as compared with the Kriging model.
Key words:aerodynamic drag, aerodynamics, airfoils, angle of attack, computational efficiency, convergence of numerical methods, design, drag coefficient, efficiency, flowcharting, force cashing, genetic algorithms, inverse problems, Mach number, matrix algebra, maximum likelihood estimation, mean square error, optimization, parameterization, Reynolds number; aerodynamic optimization design, expected improvement, GEK (gradient-enhance Kriging), infill criteria, Kriging model
中图分类号:V211.3
文献标志码:A
文章编号:1000-2758(2015)05-0819-08
作者简介:刘俊(1986—),西北工业大学博士研究生,主要从事飞行器的气动优化设计研究。
基金项目:国家高技术发展计划863项目(2012AA051301)与国家自然科学基金(11272265)资助
收稿日期:2015-03-15

