基于凸-改进遗传算法的圆阵列方向图联合优化

袁飞，杨波，黄中瑞

（合肥电子工程学院，合肥230037）

基于凸-改进遗传算法的圆阵列方向图联合优化

袁飞，杨波，黄中瑞

（合肥电子工程学院，合肥230037）

针对圆形阵列方向图具有较高旁瓣的问题，提出一种新的基于凸优化和改进遗传算法的优化方法。该方法首先采用遗传算法将阵元位置和阵元权值作为优化变量，以最小化波束方向图峰值旁瓣为目标函数进行联合优化，既增加了变量的自由度，又符合理论意义上的全局寻优；同时，为了避免算法的早熟收敛，对基本遗传算法进行了必要的改进。然后采用凸优化方法对阵元权值进行二次优化可进一步降低旁瓣电平，与传统方法相比能够明显提高优化效果的稳定性。仿真数据证实了该方法的有效性和正确性。

圆形阵列，凸优化，遗传算法，联合优化，旁瓣电平

0 引言

阵列信号处理在雷达、通信、声纳、情报信息处理、语音和医学等方面都有广泛的应用价值［1-3］，相对于目前研究较多的线性阵列而言，圆阵具有更加优越的性能。其中最为凸出的是圆阵具有对频率变化不敏感的特性［4-5］，使得它在宽带信号处理方面更具优势。

但是圆阵方向图却具有相对主瓣较高的旁瓣电平。近年来，利用稀布阵列来降低旁瓣电平的方法已成为研究热点［6］，但针对圆形阵列上的应用还较少，文献［7-12］分别就遗传算法、差分算法等智能算法对阵元权值和位置中的某个分量进行了寻优。但是归根结底这些方法无法获得较好的优化效果，因为它们只是在低维变量空间中进行优化，根本没有利用到阵元权值和位置的联合信息。文献［15］将遗传算法和凸优化结合起来对圆形阵列进行联合优化，但它是将两者进行交替使用。文献［16］采用改进遗传算法对圆针的方向图进行了联合优化，但是在得到优化结果时，无法确保阵元权值和位置的理想匹配。

1 信号模型

考虑一圆形阵列［13］，半径R=n·λ，n为一常数，λ为波长。阵列上分布了N个天线阵元，根据图1选取圆心为参考点，di为第i个单元的方位角，波束指向为（φ0，θ0）。

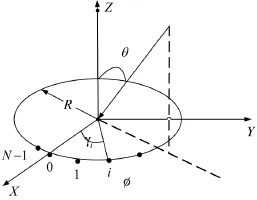
图1 圆形阵列示意图

则其方向图函数可表示为：

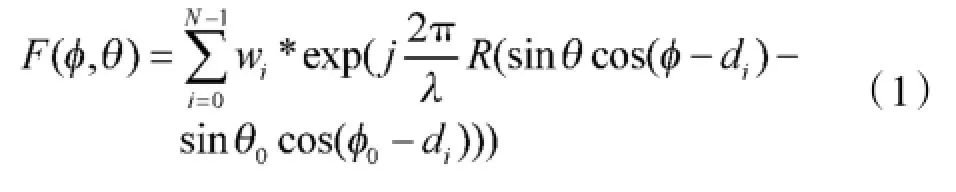
式中：wi为第i个阵元的权重；φ是起始于x轴正方向的方位角；θ是起始于z轴正方向的俯仰角。这里，重点考虑方向图随方位角的变化特性，即只考虑圆形阵列所在平面的方向图，此时θ=θ0=90°，则阵列方向图函数为：

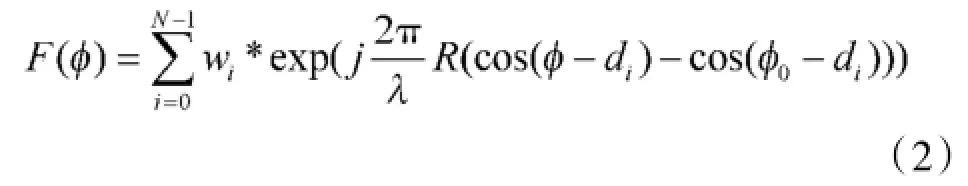
圆形阵列方向图相对峰值旁瓣电平MSLL［14］的计算公式为：

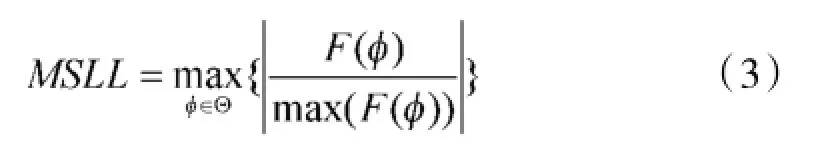
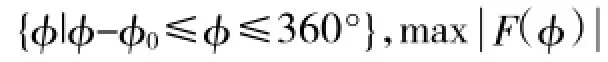
现约束相邻阵元的间隔不能小于某一个固定长度（或角度）dc，即：

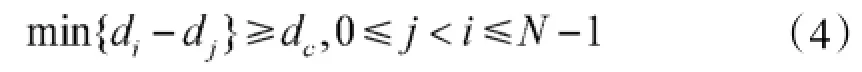
可知第N个阵元的方位角为：

将di拆分为xi+（i-1）dc，则

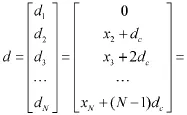
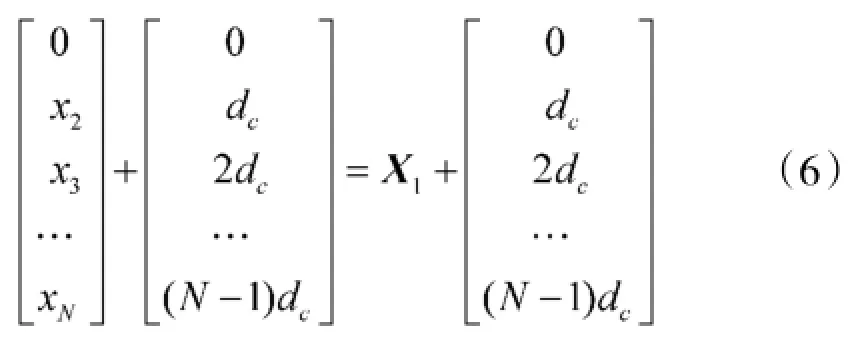
为了满足式（4），必须对向量X1的元素按从大到小的顺序排列，且有xN≤360°-Ndc，这样就将元素的搜索空间由［0，360°］减小到了［0，360°-Ndc］，提高了算法的效率。

由于圆形阵列的方向图是归一化值，所以这里限定阵元加权系数的初始群体的取值范围为［0，1］，为了提高初始染色体的随机性和后序选择、交叉、变异操作的方便性，可将复加权系数的实部和虚部分开表示为X2，X3，其为一列向量，且维数都等于阵元个数。

现将阵元位置矢量X1和阵元加权系数矢量X2，X3组合成联合优化变量的实数编码染色体X，其中X=［X1T，X2T，X3T］T，由此可得到如下的优化模型

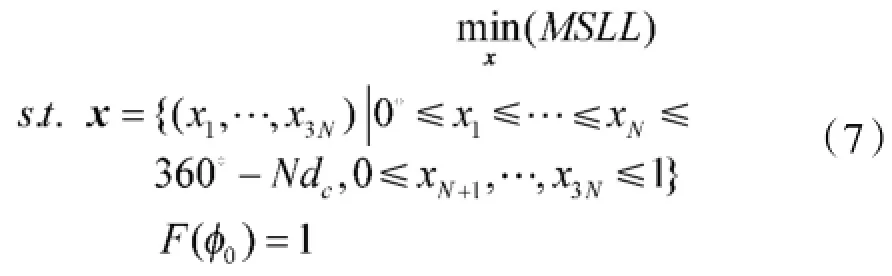
2 方向图优化算法

2.1 优化子问题描述

由式（2）、式（3）可知，式（7）所表示的目标函数具有高度非线性，属于NP难问题，可采用遗传算法进行优化求解。然而基本遗传算法存在收敛速度慢、计算结果稳定性差以及容易早熟等问题，为此对基本遗传算法进行如下改进：

（1）采用双重选择机制。在交叉之后为了保持种群的多样性和有效性，将交叉后的染色体全保留下来，然后根据适应度的大小进行排序，将前M个染色体保留下来，以保证染色体数目不变，从而完成了染色体预选。之后，采用改进轮盘赌的方法对预选染色体进行选择，以决定出实际参与交叉变异的父代个体。

（2）采用差分进化、内插/外推、单点交叉和多点交叉4种方式相结合来产生新个体，以增加种群多样性，同时采用最优个体保留策略，可有效避免算法早熟。

2.2 基于二阶锥规划的优化

通过2.1节用遗传算法对阵元位置和阵元加权系数优化后，最优变量适应度的值已经远远高于随机初始群体，若再用智能优化方法进一步寻优，最终结果不会得到太大的改善。但是，采用凸优化方法在2.1节的基础上对阵元权值进行二次加权使阵元权值与阵元位置完全匹配，可得到更好的优化效果。

由第2节的知识已知均匀圆阵的方向图函数为：

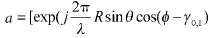
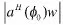
并通过对加权系数进行范数约束可以控制对白噪声增益的约束提高波束对随机误差的稳健性［9］。

这里δ为某一预设常量。

至此便得到了均匀圆阵优化波束设计的数学模型：

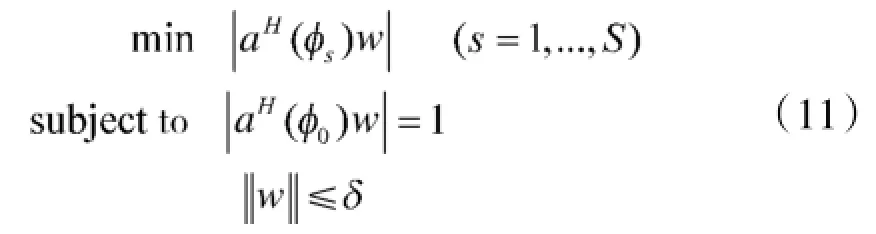
2.3 问题的SOCP形式

由矩阵理论可知，当k≥1时，任何k-范数球都是凸的，因此问题（11）是典型的凸优化问题，现进一步将此问题转化为以w的实部和虚部为变量的SOCP形式，以便为后面利用MATLAB中的工具箱SeDuMi或CVX进行高效求解打下基础，首先引入向量c，b，wr，wi，其中：

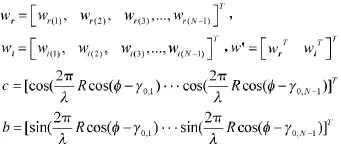
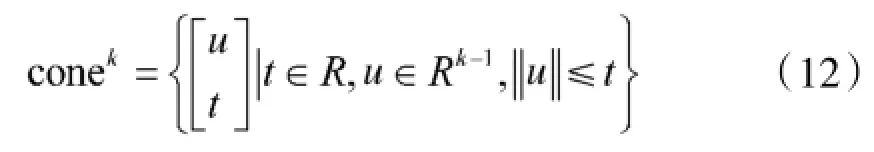
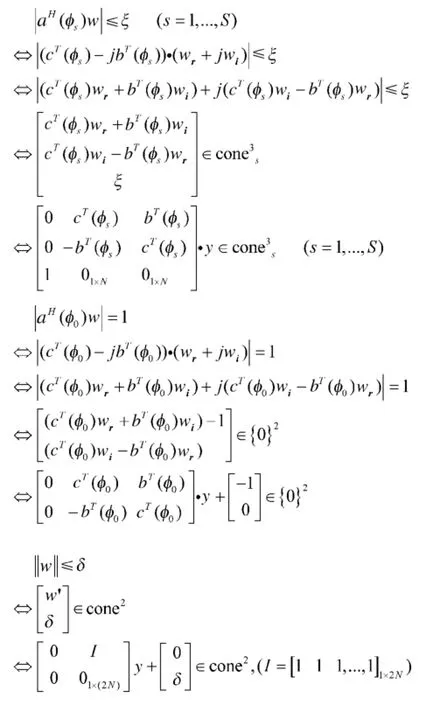
至此可得到优化模型（11）的SOCP形式：

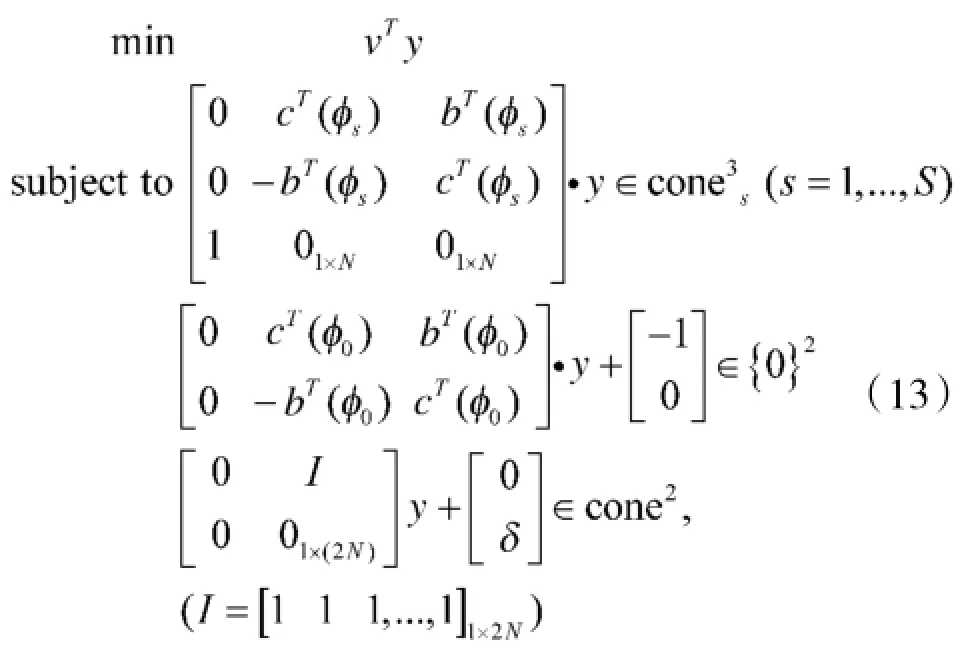
3 仿真实验

设一圆形阵列半径R=2λ，令其波束指向为（200°，90°），θ=θ0=90°，阵元数N=16，并且其相邻阵元间的最小两单位方位角差值不小于dc=14.364 1°（距离半波长）的稀布排列，取种群中个体数目M=100，最大进化代数G=200，变量维数3N=48，差分幅度控制系数F=1，内插外推系数C=0.25，α=0.05，β=0.95变异概率取0.015，主瓣的零功率点宽度2φ0=24°，旁瓣的离散化点数为138，离散化间隔约为2.5°，为了叙述方便将文献［15］的算法记为文献方法。

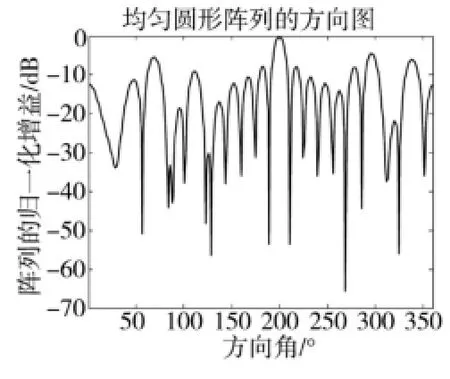
图2 阵元数为16时的均匀圆阵方向图

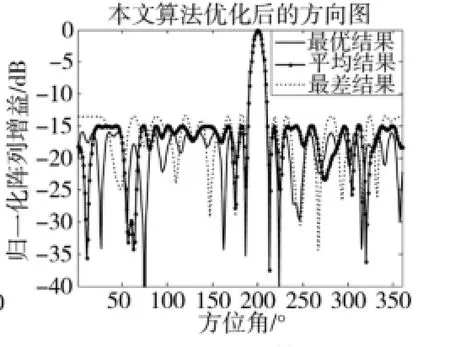
图3 本文优算法优化后的方向图

图2为均匀圆阵的方向图，最大旁瓣电平为MSLL为-4.433 6 dB。图3为应用本文算法优化后的方向图，3个方向图曲线分别为100次实验的最优，平均，最差仿真结果。其对应的最大旁瓣电平为：-15.912 7 dB、-14.642 4 dB、-13.205 2 dB，远高于文献［9-10］的-10.994 6 dB和-11.364 8 dB。

为了进一步说明本文算法的有效性以及稳定性，图,4给出了第一步中采用遗传算法对阵元位置和阵元加权系数联合优化的收敛曲线。图5为分别采用文献方法和本文方法进行100次独立实验所得的最大旁瓣电平仿真结果。

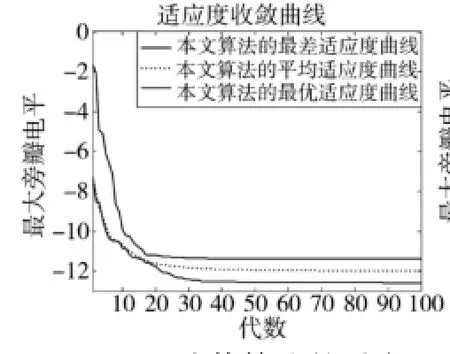
图4 遗传算法的适应度函数收敛曲线

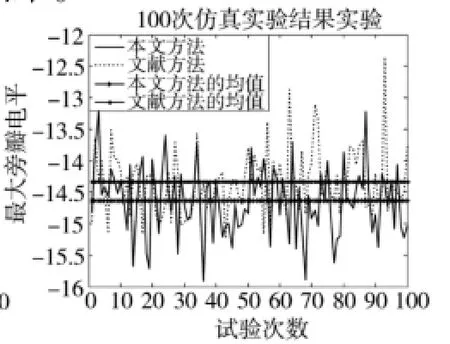
图5 本文算法和方法1的仿真结果比较

从图5中可知，两种混合优化方法都得到了较好的效果，将最大旁瓣电平降到了-14 dB左右，但本文算法的稳定性和寻优能力明显要好于文献方法。如表1、表2所示。

4 结束语

为降低圆阵方向图峰值旁瓣电平，首先，用遗传算法将阵元位置和加权系数进行联合优化，同时对基本遗传算法进行改进，避免了算法的早熟，提高了算法效率。其次，再用凸优化对阵元加权系数进行二次加权，使得阵元系数和阵元位置完全匹配，可进一步降低最大旁瓣电平。最后，仿真实验表明，利用凸-改进遗传算法对圆阵的阵元位置和加权系数进行联合优化，可获得良好的优化效果，并且相对文献方法本文具有更好的寻优性和稳定性。

表1 100次仿真实验所得的最大旁瓣电平比较

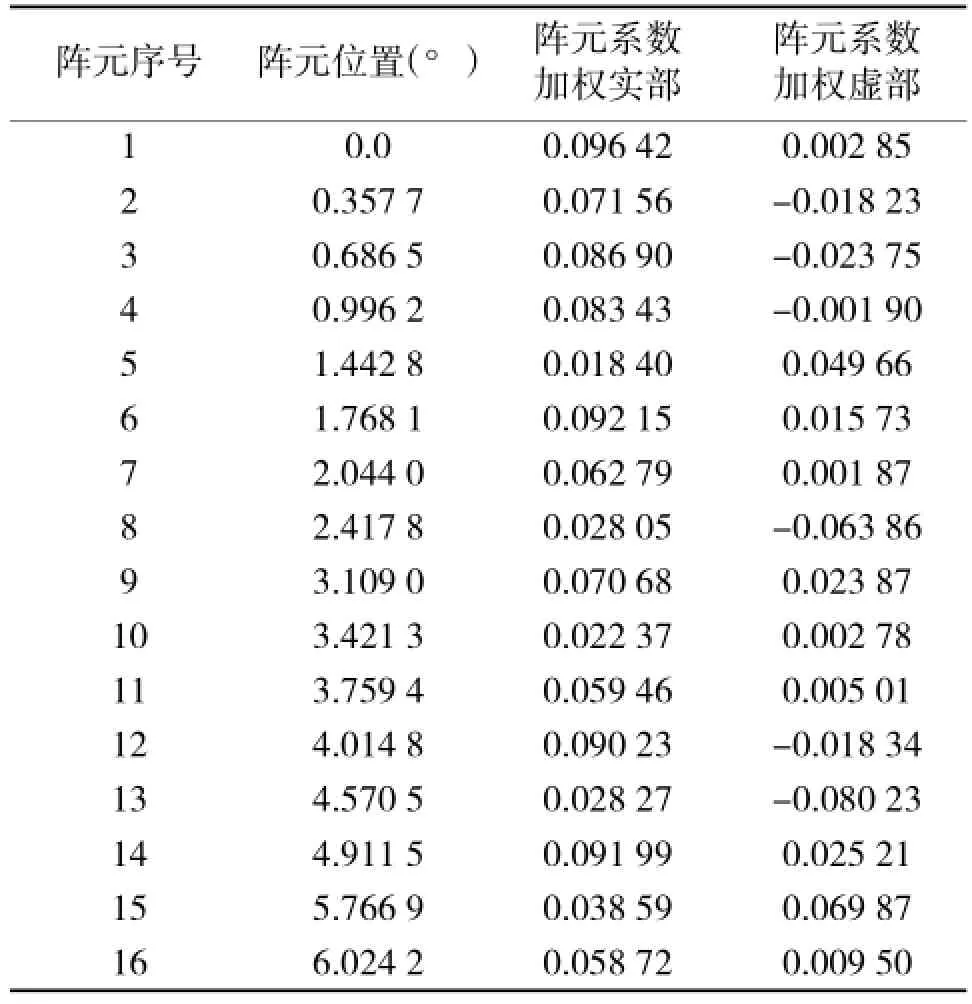
表2 优化阵元加权系数和阵元位置

［1］Mohamad G.Wideband Smart Antenna Theory Using Rect-Angular Array Structures［J］.IEEE Tran on Signal Processing，2002，50（9）：2143-2151.

［2］吴曼青.数字阵列雷达及其进展［J］.中国电子科学研究院学报，2006，1（1）：11-16.

［3］Zheng H S，Xu Z D，Jin M X.A Novel Receiver Architecture for DBF Antenna Array［J］.Journal of Electronics Science Technology of China，2007，5（1）：33-37.

［4］Steyskal H.Digital Beamforming Aspects of Wideband CircularArrays［J］.In:IEEEAerospaceConference. Piscataway，NJ:IEEE，2008（5）：1-6.

［5］穆鹏程，殷勤业，张建国.一种基于有向均匀圆阵的宽带波束形成方法［J］.中国科学：信息科学，2011，41（2）：246-256.

［6］Chen K S，Yun X H，He Z S，et al.Synthesis of Sparse Planar Arrays Using Modified Real Genetic Algorithm［J］.IEEE Transactions on Antennas and Propagation，2007，55（4）：1067-1073.

［7］王凌燕，包子阳，陈客松.圆形阵列天线优化稀布布阵方法研究［J］.中国雷达，2008（2）：1-4.

［8］Dhanesh G K，Mohamed H，Anders R.Synthesis of Uniform Amplitude Unequally Spaced Antenna Arrays Using the Differential Evolution Algorithm［J］.IEEE Transaction on Antennas and Propagation，2003，51（9）：2210-2217.

［9］包子阳，陈客松，何子述，等.基于改进差分进化算法的圆阵稀布方法［J］.系统工程与电子技术，2009，31（3）：52-55.

［10］包子阳，陈客松，何子述，等.基于改进遗传算法的圆阵稀布方法［J］.电子技术应用，2008，39（3）：19-21.

［11］周宇鹏，张争气.基于改算进遗传法的波束形成方法［J］.计算机仿真，2010，27（8）：82-93.

［12］晋军，王华力，刘苗.基于遗传算法的部分自适应波束形成方法［J］.通信学报，2006，27（12）：58-62.

［13］刘先省，张连堂，吴嗣亮，等.基于有向阵元的圆形阵列方向图综合［J］.电子学报，2004，32（4）：15-17.

［14］马云辉.基于遗传算法的唯相位控制方向图零点生成［J］.微波学报，2001，17（2）：41-46.

［15］何学辉.一种任意阵的方向图模值综合方法［J］.电子学报，2010，38（10）：65-69.

Joint Optimization about Pattern Synthesis of Circular Arrays Based on Convex Optimization and Modified Genetic Algorithm

YUAN Fei，YANG Bo，HUANG Zhong-rui
（Hefei Electronic Engineering Institution，Hefei 230037，China）

To solve the high sidelobe level of circular arrays，an optimum method based on genetic algorithm and convex optimization is presented in this paper.First，it makes the location of the array element and the coefficient as joint variables and minimizing the highest sidelobe as its fitness function via genetic algorithm.And the traditional genetic algorithm must be modified in order to avoid premature convergence.And then，the object function can be farther minimum via convex optimization. Compared with the existing pattern synthesis method，it can enhance the stability of the optimum results.Computer simulation demonstrates the efficiency and accuracy of this method.

circular arrays，convex optimization，genetic algorithm，unite optimization，sidelobe level

TN911.7

A

1002-0640（2015）01-0058-04

2013-10-20

：2014-02-18

袁飞（1986-），男，陕西泾阳人，博士。研究方向：阵列信号处理、情报分析。