伽马能谱仪中开关功率变换器非线性动力学行为

江 伟， 袁 芳

(东华理工大学 放射性地质与勘探技术国防重点学科实验室;江西省新能源工艺及装备工程技术研究中心，江西 南昌 330013)



伽马能谱仪中开关功率变换器非线性动力学行为

江 伟， 袁 芳

(东华理工大学 放射性地质与勘探技术国防重点学科实验室;江西省新能源工艺及装备工程技术研究中心，江西 南昌 330013)

为提高伽马能谱仪中开关功率变换器的工作稳定性，研究了开关功率变换器非线性行为的分析方法，其中包括数值仿真、理论分析和电路实验研究方法。以电压控制模式的Buck变换器为例，分析该变换器的工作过程，建立相应的数学模型，对该模型进行数值仿真，观察到该变换器的非线性行为。从理论上分析该现象的本质原因, 通过电路实验来验证。最后，证明这3种方法对研究开关功率变换器非线性行为的可行性和准确性，为伽马能谱仪中开关功率变换器的设计提供理论指导。

非线性； 开关功率变换器； 伽马能谱仪

0 引 言

开关功率变换器具有供电方式灵活、效率高、体积小等特点，因此，越来越多的伽马能谱仪使用开关功率变换器来供电。开关功率变换器的性能将直接影响伽马能谱仪的测试精度，测试仪器对电源的性能提出了许多特殊的要求，即在外界各种条件变化下，均能够稳定可靠地工作, 而且瞬态响应特性好[1-5]。然而，开关功率变换器是一类强的非线性系统，必定存在丰富的非线性行为，这些非线性行为可能导致输出电压不稳定，严重时可能造成系统的崩溃。因此，研究伽马能谱仪中开关功率变换器的非线性行为，对于揭示开关功率变换器非线性本质，优化开关功率变换器的设计，促进开关功率变换器性能的改进有极其重要的意义。

本文以伽马能谱仪中常用的电压控制模式的Buck变换器为研究对象，从数值仿真、理论分析、实验研究这3个不同角度来研究该开关功率变换器的非线性行为，更加深入认识该变换器的非线性现象本质，从而提高伽马能谱仪中的开关功率变换器工作稳定性能[6-10]。

1 数值仿真研究

数值仿真法在伽马能谱仪中的开关功率变换器的复杂动力学行为研究中具有十分重要的作用，它是通过使用计算机，利用数值仿真软件，对研究对象进行建模，并编制相应的仿真程序加以实现。以下对电压控制模式的Buck变换器进行数值仿真方法的研究，运用李雅普诺夫指数、功率谱等方法来描述该变换器的非线性动力学行为。

电压模式控制的Buck变换器是广泛运用的一种变换器，其基本电路如图1(a)所示，电压模式控制波形如图1(b)所示。该电路的工作过程是：输出电压Uo与参考电压Uref比较后放大得到控制电压Ucon，从tn到ts的过程，控制电压Ucon值比锯齿波电压Uramp值大，开关管G截止，二极管D导通，电感L与电容C对负载电阻供电，电感电流减少。从ts到tn+1，控制电压Ucon值比锯齿波Uramp值小，开关管G导通，二极管D截止，电源Us对电感L和电容C充电，对负载电阻供电，电感电流增大[11-15]。

根据相关的电路理论，可以列出相应的状态方程，运用Matlab/Simulink建立电压控制模式的Buck变换器的数学模型，通过对该模型进行数值仿真，可以观察电压控制模式Buck变换器的非线性动力学行为。

1.1 最大Lyapunov指数

最大Lyapunov指数可以描述系统在相空间中相邻轨道间收敛或发散的平均指数率，它是判断系统动力学行为的一个重要指标。可以通过计算最大Lyapunov指数来判断系统的工作状态。该Buck变换器的最大Lyapunov指数如图2所示，当最大Lyapunov指数小于零时，表明该系统相邻的两条轨线有收敛的趋势，变换器工作在周期状态；当最大Lyapunov指数变为正数时，表明系统相邻的两条轨线有发散的趋势，变换器工作在混沌状态；而当其由负值变为零又变回负值，表明变换器此时发生了倍周期分叉现象。

(a) Buck变换器基本电路

(b) 电压模式控制波形图

图1 电压模式控制Buck变换器及其控制波形图

图2 Buck变换器的最大Lyapunov指数

1.2 功率谱

系统进入混沌工作状态的一个重要特征是它具有连续的宽带频谱。因此，可以通过系统状态变量的功率谱来判断系统的工作状态。对于计算电压模式控制Buck变换器的功率谱，需要设置采样间隔、采样点数等相关参数，把采样数据从时域转换到频域，得出Buck变换器对应的功率谱。当参考电压Uref=11 V时，功率谱的频谱尖峰只出现在变换器工作频率处，对应为周期1状态，如图3(a)所示；当参考电压Uref=6 V或Uref=4.55 V时，功率谱的频谱尖峰出现在变换器工作频率的倍频处，对应为多周期状态，如图3(b)、(c)所示；对于混沌运动，频谱则为连续的宽带频谱，如图3(d)所示。

(a) 周期1(Uref=11.0 V) (b) 周期2(Uref=6.0 V)

(c) 周期4(Uref=4.55 V) (d) 混沌(Uref=3.0 V)

图3 Buck变换器的功率谱

运用数值仿真的方法可以对伽马能谱仪中的电压控制模式的Buck变换器的非线性动力学行为进行分析，从多角度观察该变换器的非线性现象，该研究方法方便、高效、准确。

2 理论分析

数值仿真方法可以直观地观察到变换器的复杂动力学行为。然而，在伽马能谱仪中的开关功率变换器为什么会产生非线性动力学行为是一个值得思考的问题，可以从机理上对Buck变换器进行理论分析，列出相关的解析表达式，计算判断Buck变换器失去稳定性的过程，该方法可以深刻理解开关功率变换器非线性动力学行为的本质原因。仍以电压控制模式的Buck变换器为研究对象，通过理论分析来解释开关功率变换器的稳定性。在理论分析前，以Buck开关功率变换器的工作过程为基础，运用频闪映射对变换器的数据进行采样，得到Buck变换器的离散迭代模型，然后分析该数学模型，写出该模型的雅克比矩阵，通过雅克比矩阵得到相应的特征值，依靠特征值来判别系统的工作状态。

(1)

(2)

结合式(1)和(2)，可以得出xn～xn+1的迭代映射：

(3)

式中:

(4)

由隐函数定理，雅克比矩阵:

(5)

可以获得平衡点上的特征值λ：

随着参考电压Uref的改变，雅克比矩阵的特征值的轨迹可以用图4来表示，当参考电压Uref减小到8.1 V时，1特征值越出单位圆，意味着这时Buck开关功率变换器发生分叉，从周期1状态变为周期2状态。理论分析结果与数值仿真的结果是一致的，从机理上解释了当参考电压Uref等于8.1 V时该电路失稳的原因。

图4 雅克比矩阵特征值轨迹

3 实验研究

实验研究法是研究伽马能谱仪中的开关功率变换器非线性动力学行为的重要方法。数值仿真可以直观地观察到复杂动力学行为，通过理论分析可以解释发生复杂动力学行为的原因，实验可以证实非线性行为的确存在。数值仿真和理论分析都是借助数学和计算机来进行研究，实验验证是通过设计实际的硬件电路，利用电子仪器进行观测，得出实际的测试结果，因此，具有更高的可靠性。

仍以伽马能谱仪中电压控制模式的Buck变换器为研究对象，通过实验研究的方法来观测仪器中开关功率变换器的非线性行为。通过实验可以观察到Buck变换器的工作状态(见图6)，图中，横坐标为时间变量；纵坐标分别由电容电压、锯齿波信号、电感电流组成。可以通过观测电感电流和电容电压的状态来判断系统的工作状态，当Uref=11 V时，电感电流或电容电压信号的周期是变换器开关周期的1倍，该变换器工作在周期1状态，如图5(a)所示；当Uref=6 V时，电感电流或电容电压信号的周期是变换器开关周期的2倍，该变换器工作在周期2状态，如图5(b)所示；当参考电压Uref=4.55 V时，电感电流或电容电压信号的周期是变换器开关周期的4倍，该变换器工作在周期4状态，如图5(c)所示；当Uref=3 V时，电感电流或电容电压信号的周期是变换器开关周期的无穷倍，该变换器工作在混沌状态，如图5(d)所示。这些实验观察到的数据与数值仿真得到的结论完全一致，证实了运用数值仿真、理论分析、实验研究方法对于研究开关功率变换器非线性动力学行为的可靠性。

(a) 周期1(Uref=11.0 V)

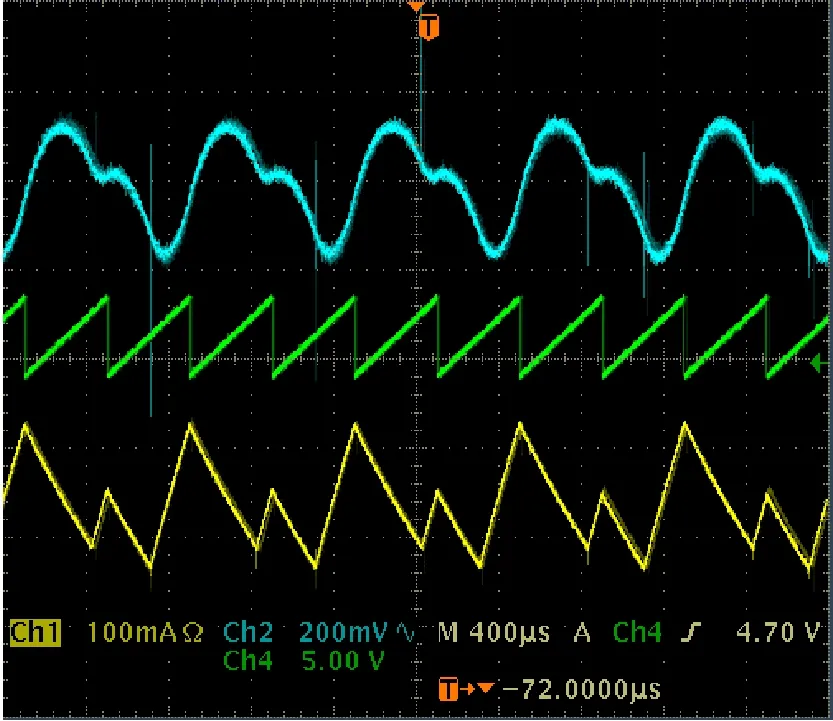
(b) 周期2(Uref=6.0 V)

(c) 周期4(Uref=4.55 V)

(d) 混沌(Uref=3.0 V)

4 结 语

本文研究了伽马能谱仪中开关功率变换器的非线

性行为，以电压控制模式的Buck变换器为研究对象，阐述了该变换器的工作过程，建立相应的数学模型，并对该模型进行数值仿真，观察到该变换器的非线性行为。通过建立精确离散映射方程，计算雅克比矩阵的特征值，从理论上分析Buck变换器发生分叉现象的本质原因。最后，通过实验研究验证了数值仿真与理论分析的一致性和正确性。该研究成果可以解释由于设计不妥而导致伽马能谱仪中开关功率变换器工作状态不稳定的原因, 为伽马能谱仪中开关功率变换器的设计提供强有力的理论指导。

[1] 张占松，蔡宣三．开关电源的原理与设计(修订版) [M]．北京:电子工业出版社，2004．

[2] 何希才．稳压电源电路的设计与应用[M]．北京: 中国电力出版社，2006．

[3] 韩广明．开关电源[M]． 北京: 中国电力出版社，2009.

[4] 王国华，王鸿麟．便携电子设备电源管理技术[M]．西安: 西安电子科技大学出版社，2004．

[5] 徐德鸿，陈 敏，陈 怡,等． 开关功率变换器 开关电源的原理仿真和计[M]．北京: 机械工业出版社，2011．

[6] 赵永科，李跃忠，胡开明. 超声波流量计信号驱动与高速切换电路研究[J]．东华理工大学学报(自然科学版)，2011，34(2):198-200．

[7] 李跃忠，朱星华, 吴伟伟.检测仪表中的数据融合方法[J]．东华理工大学学报(自然科学版)，2008，31(1)：89-92．

[8] 管小明，李跃忠，王小娟.基于MC34063的便携式仪器电源电路设计[J]．东华理工大学学报(自然科学版)，2010,33(1):97-100．

[9] 金解云，邹继军．智能交通灯控制系统的设计[J]．东华理工大学学报(自然科学版)，2011，34(3):293-295．

[10] 陈 林，杨 健，阳 浩．电子技术综合设计性实验项目[J]．实验室研究与探索，2012，31(1):149-152．

[11] 苏变玲，朱志平，袁 卫．基于 Proteus的单片机仿真教学的研究[J]．实验室研究与探索，2009，28(4): 75-78．

[12] 王兆安，刘进军．电力电子技术[M]．5版． 北京: 机械工业出版社，2009．

[13] 王宁斌．Boost变换器的控制研究与实现[D]．西安:西安理工大学，2008．

[14] 殷 健．宽输入电压范围DC-DC 变换器研究[D]．南京: 南京航空航天大学，2008．

[15] 赵 卉．电流控制模式单片开关电源的设计[D]．成都:电子科技大学，2005．

Study of Nonline Dynamical Behavior of Switching Power Converters in Gamma Spectrometer

JIANGWei,YUANFang

(Fundamental Science on Radioactive Geology and Exploration Technology Laboratory;Jiangxi Province Engineering Research Center of New Energy Technology and Equipment,East China Institute of Technology, Nanchang 330013, China)

The switching power converter is widely used in power conversion circuit, and the Gamma spectrometer provides power by switching power converter. This paper studies the analysis methods for complex behaviors of switching power converters, including numerical simulation method, theoretical analysis method, circuit experimental method to improve the operation stability of switching power converter in Gamma spectrometer. The work process of the converter is analyzed and the corresponding mathematical model is built up and simulated by taking voltage mode controlled Buck converter as an example. The nonlinear behavior can be found in the converter. The essence reason for the instability is obtained by theoretical analysis and the phenomenon can be verified by circuit. Finally, it can prove that three research methods of nonlinear behaviors to switching power converter are feasibility and accuracy. The result of study will provide theoretical guidance for the design of switching power converter in Gamma spectrometer.

nonlinearity; switching power converter; Gamma spectrometer

2014-03-17

国家自然科学基金(61064013);江西省科技支撑计划项目(20141BBG70079、2010BGB01600);放射性地质与勘探技术国防重点学科实验室开放基金项目(RGET1318);江西省学位与研究生教育教学改革项目(JXYJG-2013-074);江西省教改项目(JXJG-13-35-6);东华理工大学实验技术开发项目，国家大学生创新创业训练项目(20131005012)

江 伟(1977-)，男，江西南丰人，博士，副教授，研究方向为非线性电路与系统与测试测控技术。

Tel.：18679407781;E-mail：455302348@qq.com

TN 86

A

1006-7167(2015)01-0034-04