关于SM(L)结构的讨论
张立国,马金发
(沈阳理工大学,辽宁 沈阳 110159)
关于SM(L)结构的讨论
张立国,马金发
(沈阳理工大学,辽宁 沈阳 110159)
给出超分子的等价定义,研究超分子集合SM(L)的结构,讨论完全分配格L上SM(L)=M(L)的充要条件,为连续格理论和Fuzzy拓扑学的研究提供一些新的思路。
完全分配格;极小集;超分子
完全分配格是经典格论的重要研究对象,对其刻划的讨论一直是热点问题。无论是连续的DCPO理论,还是Fuzzy拓扑学都对其做出过相关的研究。超分子作为工具,其性质对于完全分配格的结构研究是非常重要的。文献[1]只对其进行简单讨论,但没有给出超分子集合SM(L)的结构。本文给出超分子的等价定义,讨论超分子集合SM(L)的结构,为连续格理论和Fuzzy拓扑学的后续研究奠定基础。
1 预备知识
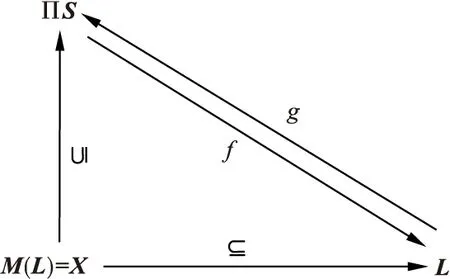
设L是完全分配格,M(L)表示L的分子集。若a∈L,以β(a)表示a的最大极小集,β*(a)=β(a)∩M(L)。可以证明a是分子当且仅当β*(a)是定向集。设a,b∈M(L),a≤b,则a< 文献[1]中引入了超分子的概念,并给出完全分配格一个比较直观的描述形式,但是未能研究超分子集合SM(L)的结构。那么超分子和分子都作为刻划完全分配格的工具,把握好他们之间的联系,有利于更好地进行格论问题的研究。 超分子的等价定义 定义1 设L是完备格,a∈L,a≠0,若∀D⊆M(L)是定向集,∨D>a,则存在d∈D使得a≤d,则称a是超分子。由超分子组成的集合,记作SM(L)。 定理1 设L是完全分配格,则SM(L)是并半格,即∀x、y∈SM(L),则x∨y∈SM(L)。 证明:设D⊆M(L)是定向集,且∨D>x∨y,则∨D>x,∨D>y。由于x、y∈SM(L),因而存在d1、d2∈D,使得x≤d1、y≤d2。又因D为定向集,存在d∈D,使得d1、d2≤d,从而x、y≤d,因此x∨y≤d,即x∨y∈SM(L)。 在完备格L上,超分子与分子不是等价概念。例如L=[0,1],1是分子而不是超分子。但在有限完备格L上,分子是超分子,而超分子不一定是分子,即M(L)⊂SM(L)。 下面给出在完备格L上超分子与分子等价条件。 命题1 设X是非空集合,则SM(2X)=M(2X)={{x}x∈X}。 定理2 设L是完全分配格,则SM(L)=M(L)当且仅当存在非空集合X,使得L≌2X。 证明:充分性 若SM(L)=M(L),而M(L)是连续的DCPO,SM(L)是并半格,则SM(L)=M(L)是连续格,从而(M(L),∑[M(L)])是入射T0空间,进而(M(L),∑[M(L)])是(或同胚)Sierpinski空间S的幂∏S的收缩核(X,Ω(X))。(不妨令M(L)=X)。由于Sierpinski空间∏S,L也是入射的locale,因此有如图1所示的关系。 图1 映射链接 由于f与g都是拓扑连续映射,故都是序同态,且为满射,从而|∏S|=|L|,因此有L≅∏S。又∏S同构某幂集格,即存在非空集合X,使得2X≅∏S,所以结论成立。 必要性 由于L≌2X,不妨设L=2X,由命题1可知,结论成立。 定理3 设L是完全分配格,则L中的每个元素都有唯一的极小集当且仅当存在非空集合X,使得L≌2X。 证明:必要性 设σ是从L→2X为序同构映射。 首先,σ、σ-1把分子映射成分子。 若A、B∈2X,且σ(a)=A∪B,则a=σ-1(A∪B)=σ-1(A)∨σ-1(B)。由于a∈M(L),因此a=σ-1(A)或a=σ-1(B),从而σ(a)=A或σ(a)=B,所以σ(a)∈M(2X)。 同理可证 若A∈M(2X),则σ-1(A)∈M(L)。 其次,σ、σ-1把极小集映射成极小集。 设a∈L。B为a的极小集,则a=∨LB,从而σ(a)=σ(∨LB)=∪σ(B),因此σ(B)为σ(a)的恰当覆盖。 再次,2X中每个元有唯一极小集,则L中的每个元素都有唯一的极小集。 设a∈L,若A、B均为a的极小集,则σ(A)、σ(B)均为σ(a)的极小集。由于2X中每个元有唯一极小集,因而σ(A)=σ(B),从而σ-1[σ(A)]=σ-1[(B)],因此A=B。 充分性 首先,设a∈M(L),必有β*(a)=↓°(a)∩M(L)。 若∀x∈β*(a),则∨[β*(a){x}]≠a。(否则:若∨[β*(a){x}]=a。由于β*(a){x}⊆β*(a),于是β*(a){x}可以加细β*(a),因此β*(a){x}是a的极小集。根据已知条件可得β*(a){x}=β*(a),矛盾),从而a∉β*(a),因此β*(a)⊆↓°(a)∩M(L)。 反之,若x∈↓°(a)∩M(L),则有x∈β*(a)。(否则:x∉β*(a)。由于β*(a)是下集,则∀y∈β*(a),都有x≤/y。 令B1={y∈β*(a)|y与x不可比}、B2={y∈β*(a)|y 若a=∨B1。由于B1⊂β*(a),因而B1是a的极小集。根据已知条件可得B1=β*(a)。又因β*(x)⊂β*(a),这与B1的定义相矛盾。 若a=∨B2。由于B2的定义可知,∨B2≤x,从而a≤x。这与x∈↓°(a)∩M(L)矛盾),因此β*(a)⊇↓°(a)∩M(L)。 其次,M(L)的序是离散的。 若b>a,必有b∉M(L)。事实上,若b∈M(L),则a∈↓°(b)∩M(L)=β*(b),因此∨[β*(b){a}]≠b。又因β*(a)⊂β*(b),且a∉β*(a),使得∨[β*(b){a}]=b相矛盾。 若θ 因此,若a、b∈M(L),且a≠b时,a与b是不可比的,即M(L)的序是离散的。 再次,令f是L到2M(L)的映射,即∀a∈M(L),f(a)=β*(a)。下面证明f为同构映射。 若a、b∈L,且a≠b时,则β*(a)≠β*(b),从而f(a)≠f(b),即f为单射。 若A∈2M(L),则∨A∈L,从而f(∨A)=A。事实上,x∈A,则∨A>x。由前面证明可知x∈β*(∨A),从而A⊆β*(∨A)=f(∨A),因此A是∨A的极小集。由于∨A有唯一的极小集,所以A=β*(∨A)=f(∨A),即f为满射。 若a、b∈L,且a 综上所述,L≌2X。 根据定理2与定理3可得如下的结论 定理4 设L是完全分配格,则下列命题等价: (1)SM(L)=M(L); (2)存在非空集合X,使得L≌2X; (3)L中的每个元素都有唯一的极小集。 由引理1和定理4可知,在有限完备格上有下面结论: 引理1[2]设L是完全分配格,则M(L)是连续的偏序集。 定理5 设L是完全分配格,且|L|<0,则SM(L)是连续的偏序集。 定理6 设L是完全分配格,且L<0,则SM(L)是完备格,从而SM(L)是连续格。 超分子作为完全分配格的研究工具,他的集合SM(L)结构是并半格。当把超分集子SM(L)与分子集M(L)联系在一起时,会得到许多很好的结论,同时也会引发新的猜想。例如完全分配格的每个元素能否被表示成SM(L)∩M(L)的元素之并、完全分配格的范畴与并半格范畴的关系、完全分配格是否存在等价范畴等,这些问题都需要进一步做出回答。 [1]张立国.完全分配格的刻划[J].浙江师范大学学报,2001,24(1):24-26. [2]郑崇友,樊磊,崔宏斌.Frame与连续格[M].北京:首都师范大学出版社,1994. (责任编辑:赵丽琴) Discussion of the Structure ofSM(L) ZHANG Liguo,MA Jinfa (Shenyang Ligong University,Shenyang 110159,China) The equivalent definition of ultra-molecule is given.The structure of the ultra-molecular setSM(L) is studied.Necessary and sufficient conditions ofSM(L)=M(L) on completely distributive latticeLis discussed.Some new ideas for the research on the theory of continuous lattices and Fuzzy topology are provided. completely distributive; minimal set; ultra-molecular 2014-11-13 张立国(1970—),男,副教授,研究方向:模糊拓扑学;通讯作者:马金发(1957—),男,高级工程师. 1003-1251(2015)04-0061-03 O189.13 A2 SM(L)结构的讨论
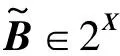
3 结束语

