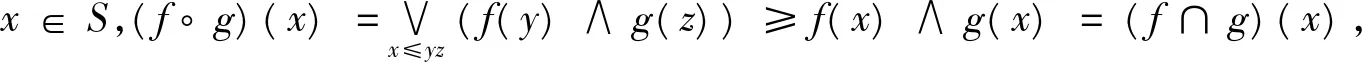m-半格的模糊理想
周 欣,赵 彬
(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)
·数理科学·
m-半格的模糊理想
周 欣,赵 彬
(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)
通过模糊集理论的方法,给出了m-半格的(素)模糊理想的概念,讨论了(素)模糊理想和(素)理想之间的关系,研究了模糊理想之集的性质。给出了(素)模糊理想和(素)理想的等价刻画,证明了含最小元的正序m-半格的像集中含1的模糊理想之集是分配l-半群。提出的方法能较好地阐述出模糊集理论与m-半格的联系。
m-半格;(素)理想;(素)模糊理想
m-半格把∨-半格的结构和半群的乘法运算结合起来,从而剩余格、Frame、Quantale和格序半群等都是特殊的m-半格。m-半格在Quantale理论的研究中有着重要的作用。Rosenthal在文献[1]中指出每一个凝聚式Quantale都同构于某个含最大元的m-半格的∨-半格理想之集构成的Quantale。众所周知,理想是刻画代数结构的重要工具之一。谢祥云在文献[2]中引入了l-半群的sl-理想的概念,并探讨了sl-理想的性质。本文受文献[2]的启发,给出了m-半格的模糊理想的概念,研究了m-半格的(素)模糊理想和模糊理想之集的性质并探讨了一些等价刻画。
1 预备知识
定义1 设(S,∨)是∨-半格,·是S上的乘法运算且满足:
(1)∀a,b,c∈S, (a·b)·c=a·(b·c);
(2)∀a∈S,a·-和-·a都保有限并,
则称(S,∨,·)是m-半格,简称S是m-半格。
由m-半格的定义知(S,·)是半群。本文给出的m-半格的定义是文献[1]引入的m-半格的定义的推广。
设S是m-半格。若∀a,b∈S,a·b≤a且a·b≤b,则称S是负序m-半格。对偶地,可以给出正序m-半格的定义。在本文中,若无特别说明,S均指m-半格。为了简便起见,用ab标记a·b(a,b∈S)。
文献[3]给出了Quantale在格与半群意义下的理想的概念。事实上这种概念可以推广到m-半格上。
定义2 设S是m-半格且I⊆S,对于下述3个条件:
(i) ∀a,b∈S,a,b∈I⟹a∨b∈I;
(ii) ∀a,b∈S,b≤a∈I⟹b∈I;
(iii)∀a,b∈S,b∈I⟹ab∈I且ba∈I,
若I满足(i)和(ii),则称I是S的∨-半格理想;若I满足(i),(ii)和(iii),则称I是S的m-半格理想,简称I是S的理想。
设P是S的理想。若P≠S且∀a,b∈S,ab∈P⟹a∈P或b∈P,则称P是S的素理想。
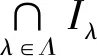

设S是m-半格且f,g∈F (S)。定义f∘g为
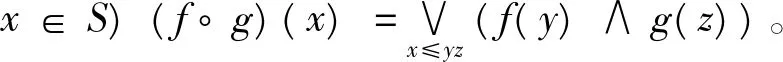
文献[5]指出运算∘满足结合律,且由文献[6]的引理2.1知若f,g,h∈F (S)且f⊆g,则f∘h⊆g∘h且h∘f⊆h∘g。
2 m-半格的模糊理想
定义3 设S是m-半格且f∈F (S),若f满足下述3个条件:
(i) ∀x,y∈S,f(x)∧f(y)≤f(x∨y);
(ii) ∀x,y∈S,x≤y⟹f(y)≤f(x);
(iii) ∀x,y∈S,f(x)≤f(xy)∧f(yx),
则称f为S的模糊理想。
设f是S的非常值的模糊理想。若∀x,y∈S,f(xy)=f(x)∨f(y),则称f为S的素模糊理想。
注1 (1) 在定义3中 (i)和(ii)可被等价替换为∀x,y∈S,f(x∨y)=f(x)∧f(y),且(iii)可被等价替换为∀x,y∈S,f(x)∨f(y)≤f(xy)。

(3) 尽管本文给出的m-半格的理想和模糊理想的概念分别与文献[3]和[7]引入的Quantale的理想和模糊理想的定义形式类似,但是从文献[3]和[7]的结论可看出这种Quantale的理想和模糊理想的定义与Quantale的乘法运算对任意并左、右分配的性质以及Quantale的完备性联系不大,所以在m-半格上使用这种定义是合适的。
例1 (1) 设I是m-半格S的理想。定义映射
f:S→[0,1]为∀x∈S,
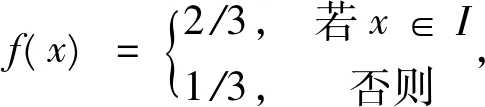
则f是S的模糊理想。
(2) 设S={⊥,a, ┬}且S上的乘法运算·为
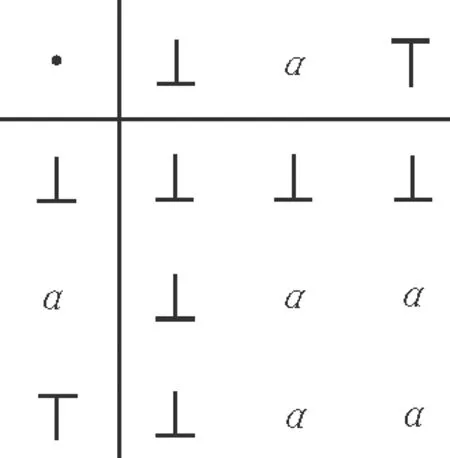
易证(S,·)是m-半格。定义S的模糊子集f为
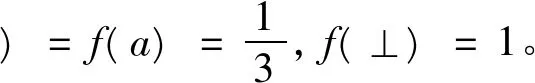
不难看出f是S的素模糊理想。
命题1 若{fλ}λ∈Λ是上定向的,则
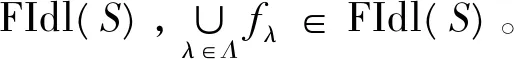
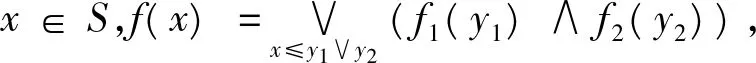



由(i)~(iii)知f是S的模糊理想。下面来证明若1∈Imf1∩Imf2,则f=f1∨f2。

命题3 设S是m-半格且f是S的模糊子集, 则f是S的模糊理想当且仅当f满足:
(1) ∀x,y∈S,f(x∨y)=f(x)∧f(y),
(2) 1S∘f⊆f且f∘1S⊆f。
证 明 与文献[6]的引理2.10的证明类似。

命题4 若S是负序m-半格,则∀a∈S,λ∈[0,1],aλ是S的模糊理想。
命题5 设aλ是负序m-半格S的序模糊点,λ∈[0,1],则1S∘aλ∘1S是S的模糊理想。
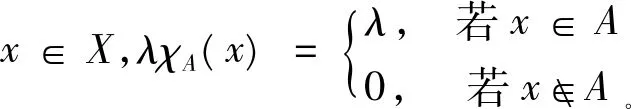
命题6 设A是m-半格S的子集,对任意λ∈(0,1]有下列结论成立:
(1)A是S的理想当且仅当λχA是S的模糊理想;
(2)A是S的素理想当且仅当λχA是S的素模糊理想。
命题7 设S是负序m-半格且f是S的非常值的模糊理想。若对任意的模糊子集g和h都成立g∘h⊆f⟹g⊆f或h⊆f,则f是S的素模糊理想。

用Q表示有理数之集,∀a∈[0,1],令Ka={t∈[0,1]∩Q:t≤a},则有a=∨Ka,从而可得到下面这个定理。
定理1 设S是m-半格且f是S的模糊子集, 则下列结论成立:
(1)f是S的模糊理想当且仅当∀t∈[0,1]∩Q,ft是S的理想;
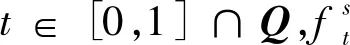
(3) 若f是S的非常值的模糊子集,则f是S的素模糊理想当且仅当∀t∈[0,1]∩Q,ft≠S⟹ft是S的素理想;
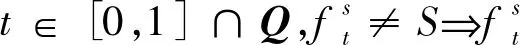
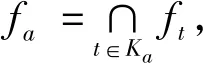
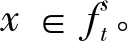
(3) 设f是S的素模糊理想。∀t∈[0,1]∩Q,由(1)知ft是S的理想。设x,y∈S且ft≠S。若xy∈ft,则f(xy)≥t。因为f(xy)=f(x)∨f(y),所以f(x)≥t或f(y)≥t,即x∈ft或y∈ft。因此,ft是S的素理想。反之,设∀t∈[0,1]∩Q,若ft≠S,ft是S的素理想。由(1)知f是S的模糊理想。设x,y∈S。若f(xy)=∧Imf,则f(x),f(y)≥f(xy),从而f(x)∨f(y)≥f(xy)。若f(xy)≠∧Imf,则∃m∈S使得f(m) (4) 证明与(3)类似。 引理1 设S是m-半格,则(Fidl(S),∘)和(FIdl(S)*,∘)是半群。 命题8 设(S,·,∨)是负序m-半格,则下列结论等价: (1)(S,·)是可换的; (2)(FIdl(S),∘)是可换的; (3)(FIdl(S)*,∘)是可换的。 (2)⟹(3) 显然成立。 (3)⟹(1) 设(FIdl(S)*,∘)是可换的。由命题4知∀a∈S,序模糊点a1∈ FIdl(S)*。∀x,y∈S,易证(xy)1=x1∘y1=y1∘x1=(yx)1。因此,xy=yx,即(S,·)是可换的。 定义4[8]设S是m-半格。若S还是格且乘法运算·还对∧左、右分配,则称S是l-半群。若S还是分配格,则称S是分配l-半群。易见l-半群是特殊的m-半格。 定理2 设S是含最小元的m-半格,则(FIdl(S)*,∘,∨,∩)是负序m-半格。特别的,若S还是正序的,则FIdl(S)*,∘,∨,∩)是分配l-半群。 证 明 已经知道(FIdl(S)*,∘,∨,∩,⊆)是格,由引理1知(FIdl(S)*,∘)是半群。设f,g,h∈FIdl(S)*,则 [1]ROSENTHALKI.QuantalesandTheirApplications[M].NewYork:LongmanScientificandTechnical, 1990. [2]XIEXY.Idealsinlattice-orderedsemigroups[J].SoochowJournalofMathematics, 1996, 22: 75-84. [3] 王顺钦, 赵彬.Quantale中的理想[J]. 陕西师范大学学报:自然科学版, 2003, 31(4): 7-10. [4]ZADEHLA.Fuzzysets[J].InformationControl, 1965, 8: 338-353. [5]KEHAYOPULUN,TSINGELISM.Theembeddingofanorderedgroupoidintoapoe-groupoidintermsoffuzzysets[J].InformationSciences, 2003, 152: 231-236. [6]XIEXY,TANGJ.Fuzzyradicalsandprimefuzzyidealsoforderedsemigroups[J].InformationSciences, 2008, 178: 4357-4374. [7]LUOQJ,WangGJ.Roughnessandfuzzinessinquantales[J].InformationSciences, 2014, 271: 14-30. [8]ANDERSONM,EDWARDSCC.Arepresentationtheoremfordistributivel-monoids[J]. Canadian Mathematical Bulletin, 1984, 27: 238-240. (编 辑亢小玉) Fuzzy ideals ofm-semilattices ZHOU Xin, ZHAO Bin (College of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062, China) By using the fuzzy set method, the concept of (prime) fuzzy ideals of anm-semilattice was introduced, the relationships between (prime) fuzzy ideals and (prime) ideals were discussed and the properties of the sets of all fuzzy ideals were studied. Equivalent characterizations of (prime) fuzzy ideals and (prime) ideals were given, and it is proved that the set of all fuzzy ideals with 1 in their images of a positivem-semilattice with a bottom element is a distributive l-semigroup.The link between fuzzy set theory andm-semilattices can be well revealed. m-semilattice;(prime) ideal;(prime) fuzzy ideal 2014-10-24 国家自然科学基金资助项目(11171196,11301316);中央高校基本科研业务费专项基金资助项目(GK201302003) 周欣,女,河南濮阳人,从事格上拓扑与模糊推理的研究。 O153.1 :ADOI:10.16152/j.cnki.xdxbzr.2015-02-0063 模糊理想之集的性质