爆炸荷载作用下方钢管混凝土柱的动力响应分析

孙 宇，毛 毳，杜欣新

(1. 天津城建大学，天津 300384；2. 天津市房屋质量安全鉴定检测中心，天津 300060)

土木工程

爆炸荷载作用下方钢管混凝土柱的动力响应分析

孙 宇1，毛 毳1，杜欣新2

(1. 天津城建大学，天津 300384；2. 天津市房屋质量安全鉴定检测中心，天津 300060)

使用ANSYS/LS-DYNA软件，建立TNT炸药、空气域以及方钢管混凝土柱的三维计算模型，模拟钢管混凝土柱在爆炸荷载作用下的动力响应，得到方钢管混凝土柱的整体响应、柱中部位移、压力以及破坏模式．结果显示：在爆炸荷载作用下，方钢管混凝土柱中部破坏最为严重，为弯曲破坏；柱脚发生剪切破坏；柱顶端出现高应力区，但并未发生严重破坏.说明由于钢管对于核心混凝土的约束作用，柱子的韧性和塑性得到较大幅度的提升.

方钢管混凝土柱；爆炸荷载；ANSYS/LS-DYNA；动力响应

近年来，国内外对钢筋混凝土柱的研究有了较大的进展[1-5]，但对钢管混凝土柱在爆炸荷载作用下的动力响应研究较少．崔莹[6]通过数值模拟复式空心钢管混凝土柱在爆炸波冲击作用下的动态响应，得出网格尺寸的大小对冲击波传播的波形和传播时间均有较大影响；冯洪波[7]研究了不同比例距离下方钢管混凝土柱的横向位移情况，结果表明，在比例距离大于2.0时，因爆炸荷载产生的方钢管混凝土柱的横向位移大幅度减小．文中运用显式动力学程序ANSYS/LS-DYNA，以共用节点分离式方式建模，空气、炸药以及钢管混凝土柱模型采用三维实体单元，深入研究了方钢管混凝土柱在爆炸荷载作用下的动态响应，包括钢管混凝土柱的整体响应、柱中部位移、压力以及破坏模式．52,cm×328,cm．炸药中心距离钢管混凝土柱表面70.76,cm，比例距离Z＝0.15．取四分之一的炸药和空气模型，二分之一的钢管混凝土柱模型，空气采用无反射边界[9]．数值模拟采用ALE算法[10-11]，模型三视图如图1所示．

1 模型建立

选用Q345和强度等级为C50的方钢管混凝土柱，柱高H为320,cm．钢管混凝土柱上端为竖向滑动端，约束x、z向位移，施加大小为0.3倍的组合轴向抗压极限承载力，以确保结构达到静力平衡；下端为固定端，约束x、y、z向位移．柱截面尺寸为35.44,cm×35.44,cm×0.886,cm；炸药尺寸为[8]40,cm×40,cm×40,cm；空气域尺寸为308,cm×

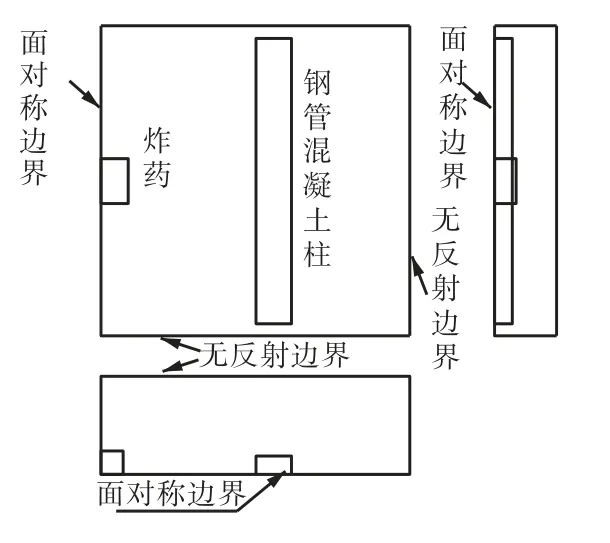
图1 建模区域三视图

2 材料模型与参数确定

2.1 空气材料模型及参数

采用MAT_NULL[12]模型来模拟理想状态空气，状态方程采用线性多项式．多项式中，相对体积V(单位体积炸药爆炸所产生的体积)和单位初始体积内能E的线性关系为

式中：γ为气体绝热指数；ρ为当前密度；ρo为初始密度；E为材料内能．

空气材料的参数见表1．

表1 空气状态方程参数

2.2 炸药材料模型及参数

模拟炸药爆轰过程中，压力与各参数的关系为

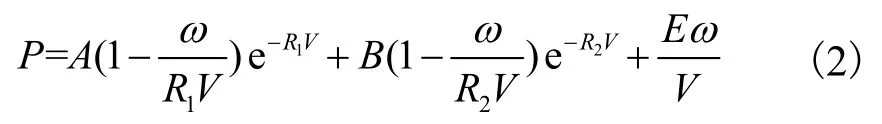
式中：A、B、R1、R2、ω为试验测得的炸药待定常数；P为爆炸所产生的压力；E为单位体积的内能；V为相对体积．TNT炸药材料的参数见表2.

2.3 钢管材料及参数

选取MAT_PLASTIC_KINEMATIC[12]材料模型对加速加载情况下钢管的应变率效应进行模拟．考虑应变速率与材料拉伸、压缩屈服强度的关系，加入Cowper-Symonds 模型，该模型应用的条件为

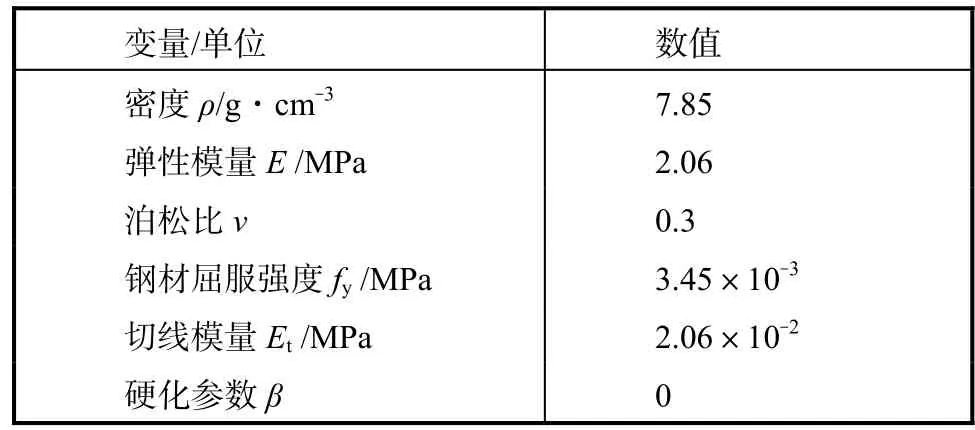
表3 钢管材料参数

2.4 混凝土材料及参数

选用混凝土强度等级为C50，具体参数见表4．

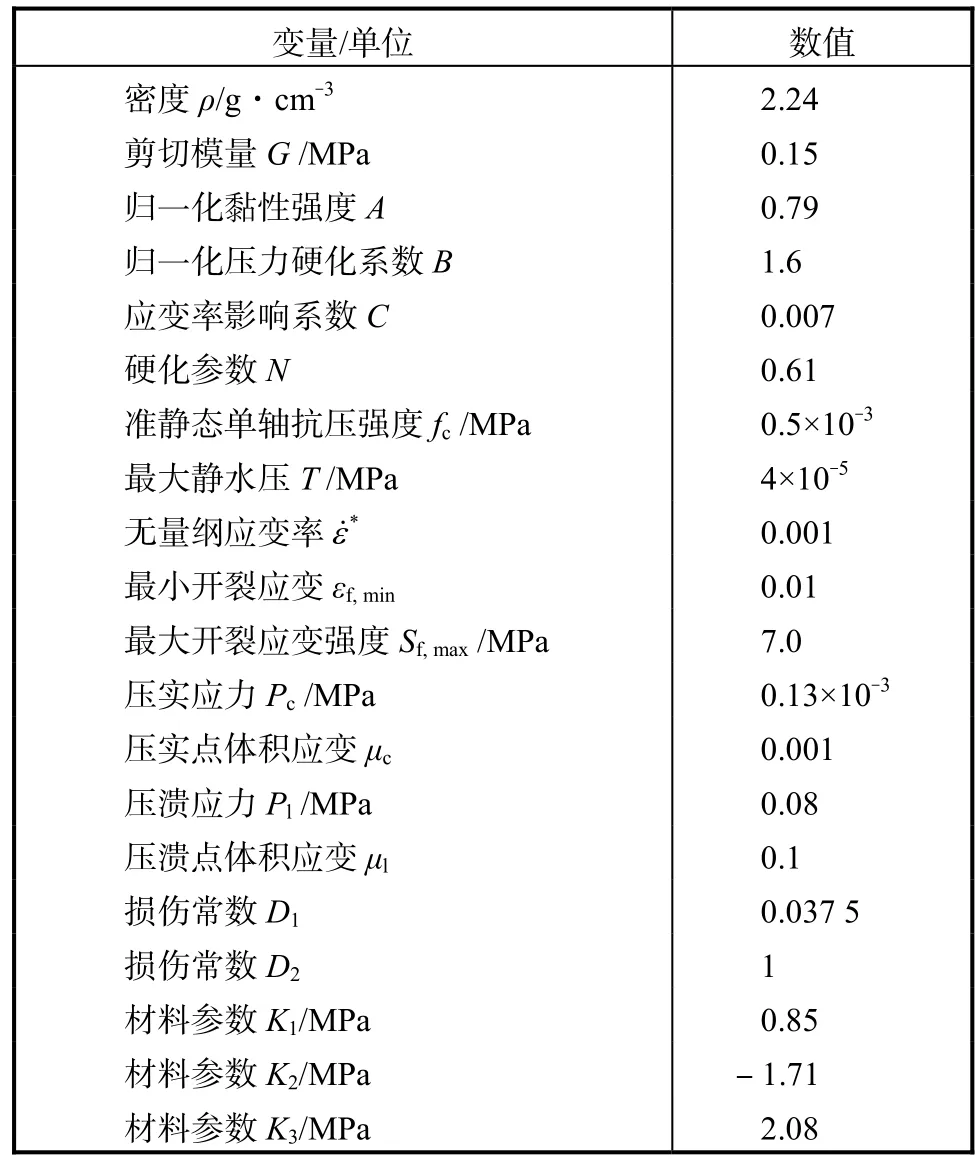
表4 混凝土材料参数

3 钢管混凝土柱在爆炸荷载作用下的动力响应

通过模拟不同炸药当量与爆炸距离情况后，在炸药与钢管之间的距离为70.76,cm、炸药量为104.96 kg，即比例距离Z＝0.15时，能最清楚地表现模型的破坏形式，故文中模型比例距离皆为Z＝0.15．设置材料失效准则为：混凝土材料主拉应变在0.001时破坏；钢材在主拉应变为0.3时破坏[13]．

3.1 钢管混凝土柱的整体响应

图2为钢管混凝土柱在爆炸荷载作用下的整体应力与应变图，其中持续时间为20,ms．由图2可以

看出：随着时间的增加，爆炸冲击波在传播到结构构件后，钢管混凝土柱中部开始向两端逐渐产生较大的塑性形变，柱中部迎爆面明显开始弯曲；在爆炸时间t＝0.79,ms时，柱中部混凝土应变达到0.001，钢管应变达到0.3，超出应变的材料退出工作；随着爆炸冲击波的继续传播，钢管混凝土柱的中部挠度逐渐增大，最后迎爆面因压应力过大，发生屈曲破坏．此时，被爆面处于受拉状态，因混凝土在钢管的约束下大大提高了其在承受冲击荷载下的塑性及韧性，因此被爆面并未发生较大破坏．在柱中点发生屈曲破坏的同时，柱端(尤其是下端)产生高应力区，并在t＝6.39,ms时，柱下端出现裂纹，随后裂纹不断扩展，柱中部的破坏也不断增大，导致钢管混凝土柱丧失承载能力．

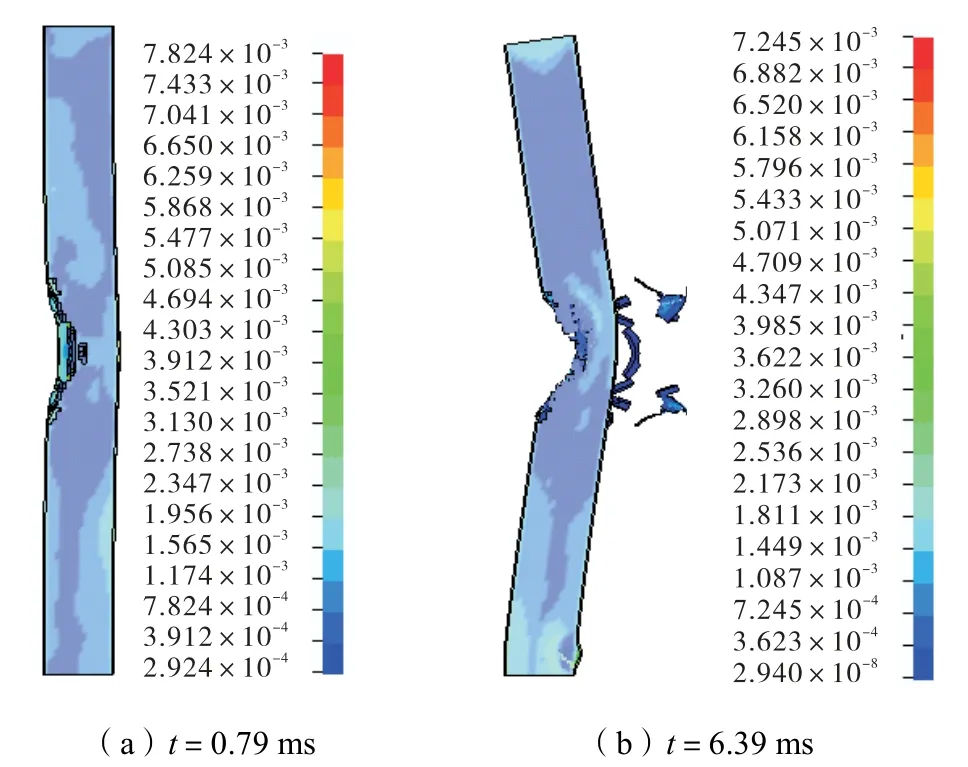
图2 钢管混凝土柱在爆炸荷载作用下的整体响应

3.2 钢管混凝土柱的柱中位移

图3为柱中点在爆炸荷载作用下的时间位移曲线，其中持续时间为100,ms．

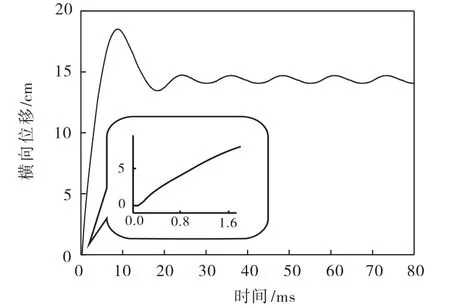
图3 钢管混凝土柱的位移时程曲线

从图3可以看出：在爆炸开始后的0～0.23,ms内，钢管混凝土柱并未发生横向(即x方向)位移，这段时间为自由空气中的炸药起爆后，冲击波在空气中的传播时间；在0.23,ms后，钢管混凝土柱中部沿爆炸冲击波传播方向(即x轴正方向)位移迅速增加；在12.60,ms时达到最大，最大横向位移为18.52,cm，此位移相当于柱长的6.17%,；随后，钢管混凝土柱的横向位移逐渐减小，在30,ms后达到平衡，并在14.53,cm处振动，幅值约为3.53,cm．

3.3 钢管混凝土柱的压力及破坏模式

取钢管混凝土柱的柱中点、柱顶端中点以及柱底端中点，对钢管混凝土柱所受冲击波压力(即超压值)变化进行分析．图4为各单元的压力时程曲线，其中持续时间为40,ms．

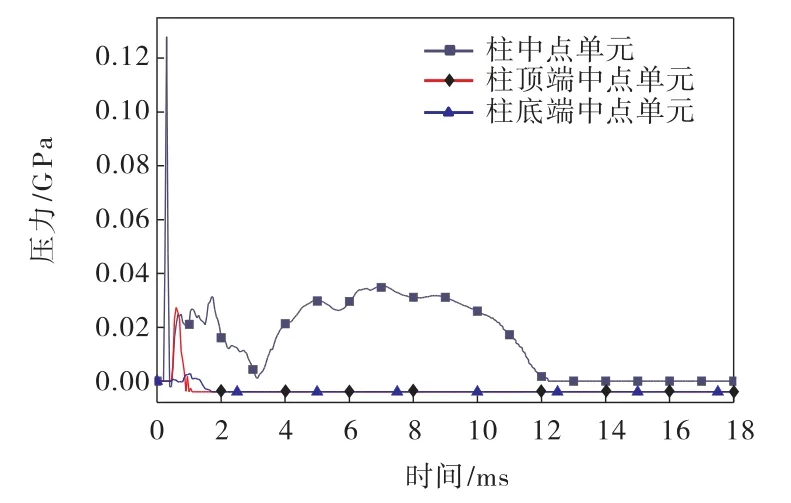
图4 钢管混凝土柱的压力时程曲线

从图4可以看出：柱中点、柱顶端中点以及柱底端中点三处在0～0.20,ms内所受压力为0，即冲击波到达钢管混凝土柱时间为0.20,ms．由于炸药处于柱中点前方爆炸，因此，当爆炸冲击波到达柱面后，柱中点部分受到较大的压力，并在短时间内压力急剧增大，最大值为129.45,MPa，此时钢筋和混凝土均未达到屈服极限，仍能继续工作；随后压力值随着气温的降低，最终降到0,MPa．

钢管混凝土柱上、下端中点所受压力在0～0.45,ms内均为0，柱上端在0.99,ms时达到最大值，其超压峰值为0.528,MPa；柱下端在0.49 ms时达到最大值，其超压峰值为2.66,MPa．因为边界条件的不同，柱上端为竖向滑动端，柱脚为固定约束端，故柱头所受到的压力比柱脚稍小．与柱中部超压值类似，柱两端的压力值随着气温的降低，最终降到0,MPa．

随着爆炸入射波以及发生反射形成拉伸波相互叠加后，继续作用在钢管混凝土柱上，柱中主要发生延性的弯曲破坏，柱中迎爆面为主要破坏部分，其最大有效塑性应变达到0.46；柱脚由于约束形式为固定约束，逐渐开始发生剪切破坏，破坏主要出现在被爆面．钢管和混凝土的破坏形态如图5所示(t＝15.21,ms)．

图5 钢管和混凝土在爆炸荷载作用下的破坏形态

4 结 论

(1)钢管混凝土结构构件在受爆炸冲击波作用的过程中，能够更好地抵抗短暂作用的爆炸荷载．

(2)当炸药位于钢管混凝土柱中正前方时，柱中产生较大位移，迎爆面大部分区域内部混凝土发生压溃破坏；而背爆面由于没有受到爆炸波正面冲击，且结构本身的承载能力较强，并未发生明显破坏．

(3)在爆炸荷载作用下，钢管混凝土柱因上下端约束不同，受到的冲击波超压值也不相同，固定端相对于滑动端受到冲击波压力值更大．

(4)爆炸荷载作用下，钢管混凝土柱的破坏模式主要为弯曲破坏和剪切破坏．弯曲破坏主要发生在柱身迎爆面，而剪切破坏主要发生在柱脚．因此，可对柱身迎爆面及柱脚处混凝土进行加固，以延长构件在爆炸荷载作用下的工作时间．

［1］ 师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津：天津大学，2009.

［2］ 阎 石，齐宝欣，辛志强，等. 高温与爆炸作用下轻钢柱动力响应与破坏模式数值分析[J]. 土木工程学报，2010，43(增刊)：484-489.

［3］ SHI Yanchao，HAO Hong，LI Zhongxian. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering，2008，35(11)：1,213-1,227.

［4］ 徐慎春. 爆炸荷载作用下超高性能钢筋混凝土柱抗爆性能研究[D]. 天津：天津城建大学，2013.

［5］ MUTALIB A A，HAO Hong. Development of P-I diagrams for FRP strengthened RC columns[J]. International Journal of Impact Engineering，2011，38(5)：290-304.

［6］ 崔 莹. 爆炸荷载下复式空心钢管混凝土柱的动态响应及损伤评估[D]. 西安：长安大学，2013.

［7］ 冯洪波. 爆炸荷载作用下的钢管混凝土柱的动力响应研究[D]. 西安：长安大学，2008.

［8］ DU Hao，LI Zhongxian. Numerical analysis of dynamic behavior of RC slabs under blast loading[J]. Transactions of Tianjin University，2009，15(1)：61-64.

［9］ 师燕超，李忠献. 爆炸荷载作用下钢筋混凝土结构破坏倒塌分析研究进展[J]. 土木工程学报，2010，43(增刊)：83-92.

［10］ NAM J W，KIM H J，KIM S B. et al. Numerical evaluation of the retrofit effectiveness for GFRP retrofitted concrete slab subjected to blast pressure[J]. Composite Structures，2010(92)：1,212-1,222.

［11］ TAI Y S，CHU T L，HU H T，et al. Dynamic response of a reinforced concrete slab subjeted to air blast load[J]. Theoretical and Applied Fracture Mechanics，2011：56(3)：140-147.

［12］ Livermore software technology corporation. LS-DYNA keyword user’s manual[M]. California：Livermore Software Technology Corporation，2007.

［13］ 杜欣新，毛 毳. 网格划分影响二维爆炸冲击波数值模拟精度的研究[J]. 天津城市建设学院学报，2013，19(4)：277-279.Dynamic Response Analysis of Concrete Rectangular Steel Tube Columns Under Blasting Loading

SUN Yu1，MAO Cui1，DU Xin-xin2
(1. Tianjin Chengjian University，Tianjin 300384，China；2. Tianjin Housing Center for Evaluation and Inspection of Quality and Safety，Tianjin 300060，China)

3D calculation model of TNT explosive，air domain and concrete rectangular steel tubular column are established by software ANSYS/LS-DYNA. To obtain the overall response and central displacement of concrete rectangular steel tubular columns，pressure，and failure mode，the dynamic response of concrete rectangular steel tube columns under blast loading is simulated. The results show：that the explosive destruction in middle part of the steel tube concrete column is most serious，which is bending failure；the root of column shear is failure；the high stress area exists in the column top，but has no serious damage. The results of this study show that，due to the steel tube，concrete filled steel tube has higher toughness and plasticity in three dimensional stress states.

concrete rectangular steel tubular column；blast loading；ANSYS/LS-DYNA；dynamic response

TU375.3

A

2095-719X(2015)04-0258-04

2014-12-17；

2015-04-02

孙 宇（1990—），男，湖南岳阳人，天津城建大学硕士生.