改进小波序贯极限学习机的光电经纬仪空间配准算法研究

杨宏韬高慧斌刘 鑫

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.长春工业大学电气与电子工程学院，吉林 长春 130012）

改进小波序贯极限学习机的光电经纬仪空间配准算法研究

杨宏韬1，2，3，高慧斌1，刘 鑫1

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.长春工业大学电气与电子工程学院，吉林 长春 130012）

针对光电经纬仪数据融合系统中的空间配准问题，提出复合函数小波神经网络序贯极限学习机光电经纬仪空间配准算法。该算法将小波理论引入到极限学习机中，利用小波函数和任意分段连续非线性函数构造极限学习机隐层节点激励函数，小波函数的伸缩因子和平移因子根据输入数据范围进行初始化，并结合极限学习机在线学习方法进行训练。实验结果表明：改进小波序贯极限学习机的光电经纬仪空间配准算法可以使光电经纬仪的测量精度提高到3″以内，与标准极限学习机空间配准算法相比，该算法能够实现在线增量式快速学习，具有更好的泛化性能。

光电经纬仪；空间配准；小波神经网络；序贯极限学习机

0 引 言

光电经纬仪多传感器数据融合系统中，采用融合技术综合处理长波红外、中波红外、可见光等传感器的量测数据，可以增大量测范围、提高目标跟踪能力、增强系统可靠性及跟踪准确度。由于系统中各传感器存在系统误差,量测轨迹并不重合，直接进行融合将导致跟踪准确度降低，难以发挥多传感器融合的优势。所以量测数据融合前需要进行空间配准以消除各传感器的系统偏差[1]。国内外学者为了解决多传感器的空间配准进行了大量的研究，文献[2]结合目标的运动状态和传感器系统误差构建扩维系统动态方程,提出了迭代扩展卡尔曼滤波（IEKF)的配准算法,能取得和UKF相近估计精度。文献[3]对机动平台的传感器系统误差、目标状态进行期望最大化迭代，并对目标的状态进行融合估计，提出离线机动极大似然配准（MLRM)算法，有效估计出量测、姿态角系统误差和目标状态。文献[4]采用扩展卡尔曼滤波通过非线性转换坐标机动模型，分别对每个传感器的位置误差和方位误差进行估计，准确计算出公共参考坐标系下的三坐标雷达的位置与方位误差。上述方法都是在假设系统偏差为固定偏差集合的基础上取得了不错的配准效果，而忽略了影响系统偏差的许多不确定因素[5]。

单隐层前馈神经网络（single-hidden layer feedforward neural networks，SLFNs)具有的非线性辨识能力，使其在多传感器空间配准领域得到了广泛应用。文献[6]在各类传感器系统偏差来源未知的前提下运用神经网络进行偏差配准。与传统SLFNs不同，极限学习机（extreme learning machine，ELM)使用求解线性方程组方法对神经网络进行训练，训练时输入层与隐含层的网络权值以及隐含层阈值随机生成，仅求解矩阵广义逆得到隐含层与输出层网络权值，训练时间大幅缩短。文献[7]采用极限学习机算法建立光电经纬仪空间配准模型。虽然上述两种方法解决了系统偏差假设问题，但是存在泛化能力低、网络训练时间较长、难以得到全局最优解、难以实现在线学习等问题。

文献[8]在ELM[9]基础上提出在线序贯极限学习机 (online sequential extreme learning machine，OS-ELM)，该算法训练时只对新数据进行学习，而不必连同之前历史数据重新训练，新数据一旦学习结束即可丢弃，其本质为ELM的在线增量式快速学习算法。文献[10]指出由于输入数据的变化OS-ELM算法的稳定性随之变化较大，隐层节点激活函数的问题依赖性导致该算法泛化性下降。

本文将小波的时频局部特性、聚焦特性[11]，神经网络的自学习、自适应、鲁棒性以及序贯极限学习机的在线学习能力相结合，提出复合函数小波神经网络序贯极限学习机（composite function wavelet neural networks with online sequential extreme learning machine，CFWNN-OSELM)空间配准算法，网络的隐层节点激活函数由小波函数和任意分段连续的非线性函数构成，小波函数的伸缩、平移因子根据输入数据的范围进行初始化，并结合极限学习机序贯学习方法对小波神经网络进行训练。通过光电经纬仪的星体测量数据进行模型验证，并与ELM空间配准算法进行对比。结果表明，该算法具有更快的学习速度和更强的泛化能力，达到了提高光电经纬仪测量精度的目的。

1 CFWNN-OSELM概述

1.1 CFWNN结构

复合函数小波神经网络结构与传统的小波神经网络相比，除了在输入层增加了非零偏置x0，更主要的是隐层节点使用经过平移与尺寸伸缩的母小波函数与任意分段连续非线性函数构成的复合函数作为激活函数。复合激活函数比单一使用小波函数更加紧凑，适当选取小波函数的伸缩因子和平移因子，能保证小波函数覆盖输入数据范围，这时CFWNN将具有良好的逼近能力[12]。CFWNN的结构如图1所示。

图1 CFWNN的结构

对于N个任意训练样本（xi，ti)，其中xi=[x0，xi1，xi2，…，xin]T∈Rn，ti∈Rm，对于具有L个隐层神经元的CFWNN，可记为

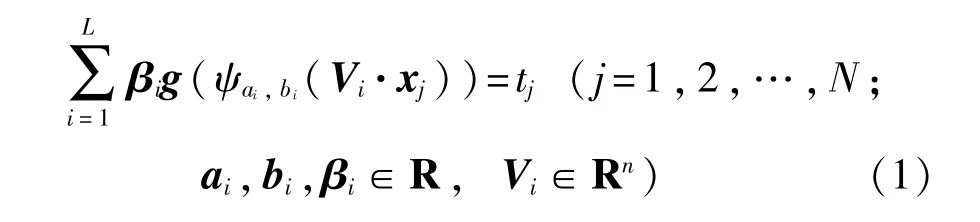
式中：Vi=[νi1，νi2，…，νin]T∈Rn——连接输入层神经元与隐层第i个神经元的权值；

βi——连接隐层第i个神经元和输出层神经元的权值；

ψai，bi（·)——隐层第i个神经元的小波函数；

ai，bi——伸缩因子和平移因子；

g（·)——任意分段连续非线性函数。

式（1)可以改写为Hβ=T，其中，H称为CFWNN的隐层输出矩阵。

1.2 小波参数的初始化

隐层小波函数的伸缩因子和平移因子初始化是CFWNN-OSELM空间配准算法的关键，本文根据输入数据的范围对参数进行初始化。首先，随机选择输入权值矩阵V，设[xi，min，xi，max]表示第i个输入数据的范围（不考虑x0)，则隐层节点复合函数输入值范围表示为L。t*、ψ*分别表示小波函数的时窗中心和时窗半径，则第h个隐层神经元的小波函数ψah，bh的时窗为[bh+ah（t*-ψ*)，bh+ah（t*+ψ*)]。为了保证小波函数能覆盖输入数据范围，得到如下等式：

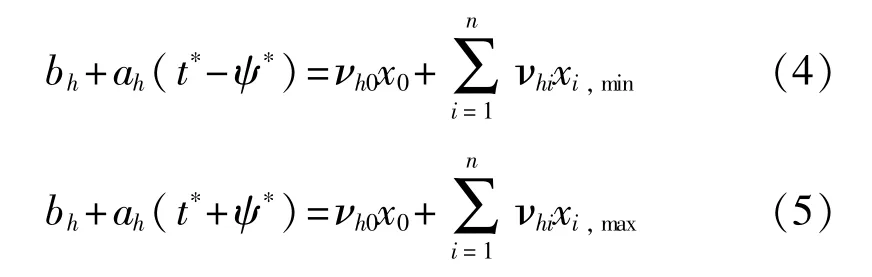
由式（4)、式（5)得出伸缩因子和平移因子初始化公式：

小波函数的时窗中心和时窗半径由下式得出：

1.3 CFWNN-OSELM学习算法

CFWNN-OSELM学习算法分为初始化阶段和序贯学习阶段，计算步骤为：

1)初始化阶段：从给定训练集N={（xi，ti)|xi∈Rn，ti∈Rm，i=1，2，3，…，n}中选取少量的初始训练集N0=其中N0≥L，进行初始化学习。a)随机分配输入权值Vi，按照式（6)、式（7)初始化伸缩因子ai和平移因子bi，i=1，…，L。

b)计算初始隐层输出矩阵H0

d)令k=0。

a)计算隐层节点输出矩阵Hk+1

d)令k=k+1。转到步骤2)继续执行。

上述推导过程可知，该算法只对新来的数据集进行学习，并且数据集长度可变，从而提高了算法的运行速度。在对网络参数初始化时，除了对小波参数进行初始化外，只需确定隐层神经元个数，降低了网络参数之间的依赖性。

2 实验结果与分析

为了分析ELM和CFWNN-OSELM算法的训练时间和配准效果，采用某型号光电经纬仪测量的36颗恒星数据进行仿真实验，将其中3190组测量数据作为训练数据，其余的350组作为测试数据，部分测量数据如表1所示。

CFWNN-OSELM算法的输入为非零偏置、方位和俯仰实测值，输出为方位、俯仰测量误差。CFWNNOSELM算法的隐层神经元个数为30，隐层节点激活函数由经过平移和伸缩的Morlet小波函数ψ（t)=cos（1.75t)e-0.5t2和“Sigmoid”函数g（x)=1/（1+e-x)构成。ELM算法的隐层神经元个数为30，隐层节点激活函数选择“Sigmoid”函数。设定ELM与CFWNNOSELM算法初始化学习阶段样本数为200，序贯学习阶段的每次学习的样本数为1。在仿真实验时，输入数据标准化至[-1，1]之间，输出数据标准化至[0，1]之间。仿真实验均在2.5GHz的Intel CPU、4GB RAM和Matlab 7.10.0环境下进行。两种配准算法测试时输出的误差曲线及性能对比如图2、表2所示。

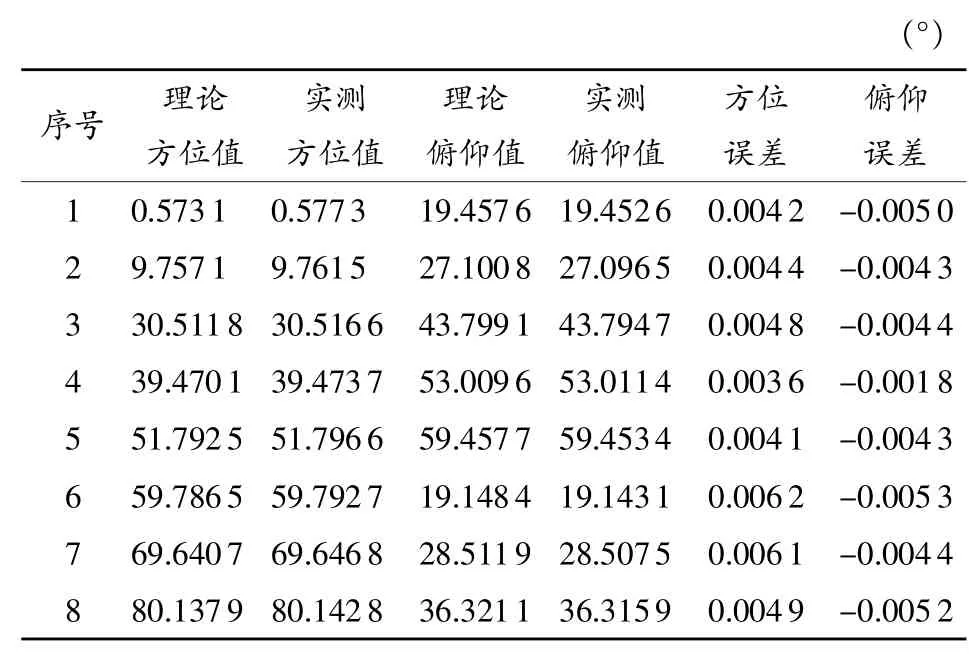
表1 部分恒星测量数据

图2 测试误差比较图

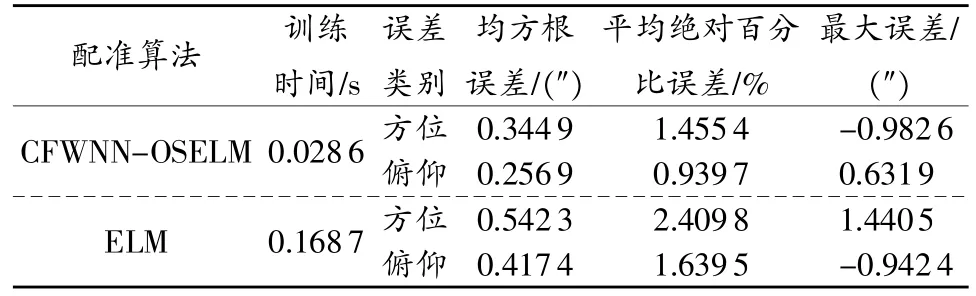
表2 配准性能对比

可以看出CFWNN-OSELM与ELM相比，在配准准确度上有一定程度的提高，但是CFWNN-OSELM的训练时间明显小于ELM，这是由于标准ELM算法采用批量学习方式，当新数据输入时，需要对所有数据重新训练，训练时间主要消耗在计算矩阵H∈RN0×L的Moore-Penrose广义逆；而CFWNN-OSELM算法在初始化学习阶段只计算一次L×L矩阵的逆运算，由式（12)可知在序贯学习阶段训练时间的消耗与每次学习的样本数量有关，样本数量越少学习时间越短。

由此可知，CFWNN-OSELM算法的快速学习特性与在线学习阶段每次学习的新数据的样本数量有关，在对实时性要求较高的情况下，应该选择较少的新数据样本数量。

图3 原始测量误差

图4 CFWNN-OSELM算法配准后的测量误差

为验证CFWNN-OSELM算法的效果，用光电经纬仪对能够提供精确轨道数据的激光卫星（LASER Satellite)进行跟踪测量。图3是光电经纬仪对某激光卫星的原始测量误差，图4是CFWNN-OSELM算法配准后的测量误差。

可以计算出原始测量中的方位、俯仰平均绝对误差分别为-11.0504″、-4.1582″，配准后的方位、俯仰平均绝对误差分别为0.2017″、0.6947″，配准后测量准确度大幅提高。对两颗激光卫星进行一段时间的连续跟踪测量，结果见表3，进一步验证了CFWNNOSELM空间配准算法提高光电经纬仪测量精度的可行性。

表3 CFWNN-OSELM配准后测量准确度

本文提出的空间配准算法适用各类偏差来源未知传感器系统，且实时性要求较高的光电经纬仪多传感器数据融合系统中，使用该算法直接对测量结果进行修正，再进行数据融合可以进一步提高光电经纬仪的跟踪准确度。

3 结束语

本文针对如何有效解决光电经纬仪数据融合系统中的空间配准问题，提出了一种新的空间配准算法CFWNN-OSELM，该算法具有序贯极限学习机在线快速学习的特点，引入小波函数和任意分段连续非线性函数构成隐层节点激活函数，以增加配准算法的局部分辨能力，根据输入数据的范围对小波函数的伸缩、平移因子进行初始化，从而得到更好的泛化性能。最后通过星体测量数据进行模型验证，结果表明该算法可以使光电经纬仪的测量准确度提高到3″以内，达到了修正光电经纬仪测量误差的目的，并且具有更快的学习速度和更强的泛化能力，为提高光电经纬仪的测量准确度提供了新的方法和思路。

[1]刘瑜，何友，王海鹏，等.基于平方根容积卡尔曼滤波的目标状态与传感器偏差扩维联合估计算法[J].吉林大学学报：工学版，2015，45（1)：314-321.

[2]李军辉，杨峰，程咏梅，等.一种多传感器实时误差配准算法研究[J].传感技术学报，2010，23（5)：713-716.

[3]崔亚奇，熊伟，何友.基于MLR的机动平台传感器误差配准算法[J].航空学报，2012，33（1)：118-128.

[4]Nassib N，Robort H.Bishop solution to a multisensor tracking problem with sensor registration error[J].IEEE T-AES，1999，35（1)：354-363.

[5]余建国，刘梅，包玖红.基于星光测量天基传感器实时定标在弹道目标跟踪应用[J].电子与信息学报，2013，35（4)：915-920.

[6]Karmiely H，Hava T S.Sensor registration using neural network[J].IEEE Transactions on Aerospace and Electronic Systems，2000，36（1)：85-100.

[7]杨宏韬，高慧斌，张淑梅.极限学习机方法在经纬仪空间配准中的应用[J].红外与激光工程，2013，42（12)：3517-3521.

[8]Liang N Y，Huang G B，Saratchandran P，et al.A fast and accurate online sequential learningalgorithm for feedforward networks[J].IEEE Transactions on Neural Networks，2006，17（6)：1411-1423.

[9]Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：theory and applications[J].Neurocomputing，2006，70（1)：489-501.

[10]Lan Y，Yeng C S，Huang G B.Ensemble of online sequential extreme learning machine[J].Neurocomputing，2009，72（1)：3391-3395.

[11]全丽萍，李晓理，王巧智.多分辨率小波极限学习机[J].北京科技大学学报，2014，36（12)：1712-1719.

[12]Cao J W，Lin Z P，Huang G B.Composite function wavelet neural networks with extreme learning machine[J]. Neurocomputing，2010（73)：1405-1416.

Research on modified wavelet online sequential extreme learning machine in space registration for photoelectric theodolite

YANG Hongtao1，2，3，GAO Huibin1，LIU Xin1
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China；3.College of Electronic and Electrical Engineering，Changchun University of Technology，Changchun 130012，China）

An algorithm using composite functions and wavelet neural networks（WNN）in online sequential extreme learning machines（OS-ELM）was proposed to solve the problem in the space registration of photoelectric theodolite data fusion system.The wavelet theory was introduced to extreme learning machines and the wavelet function and bounded non-constant piecewise continuous function were used to build an hidden-node excitation function for extreme learning machine.The contraction-expansion and shift factors of the wavelet function were initiated with the input data range and it was trained in combination with the online learning methods of extreme learning machine.Experimental results show that this algorithm can improve the measurement accuracy of photoelectric theodolite to within 3″and has fast online learning speed and good generalization compared with standard space registration algorithms.

photoelectric theodolite；space registration；WNN；OS-ELM

A

：1674-5124（2015）10-0001-05

10.11857/j.issn.1674-5124.2015.10.001

2015-02-26；

：2015-04-13

国家863计划项目（2008AA0047)

杨宏韬（1982-)，男，吉林长春市人，博士，研究方向为光电测量与信息融合。