膨胀管可靠性评价方法研究
李 涛,丁爱芹,陈 强,李益良,裴晓含,张 涛
中国石油勘探开发研究院采油采气装备研究所 (北京 100083)
膨胀管技术是一种由特殊材料制成、具有良好塑性的金属钢管,下入井内后进行膨胀,在冷作硬化效应下,管材力学性能得到提高[1-3],在管柱设计过程中,通常使用传统的安全系数法,即将各因素的最大值(如外挤力)和名义值(如内外径)等固定值代入模型之中,得出一个确定的安全系数,但是受到塑性变形、残余应力等多重不确定因素影响,使用安全系数法设计膨胀管管柱存在较大的主观随意性。
通过分析不同膨胀率条件下膨胀管胀后抗外挤强度以及残余应力的变化规律,同时考虑到膨胀管膨胀过程中屈服强度、外径、壁厚、椭圆度、残余应力等参数变化的随机性,利用可靠性理论建立膨胀管外部载荷与失效概率的安全评价方法。
1 胀后膨胀管力学性能
通常认为膨胀管膨胀属于冷作硬化过程,胀后膨胀管屈服强度与抗拉强度提高,延展率下降,残余应力变大。膨胀率是描述膨胀管胀后尺寸的重要参数,对膨胀管力学性能以及可靠性有重要影响,利用有限元分析114mm×7mm规格碳钢材料膨胀管在不同膨胀率条件下力学性能的变化规律。图1为膨胀管塑性变形过程以及胀后等效应力云图。膨胀过程中在膨胀的部位即膨胀锥所在的位置出现等效应力最大的红色区,膨胀后应力得到了释放。
膨胀管膨胀过程中,在环向、轴向及径向都将发生塑性变形,这种塑性变形往往是不均匀的,不均匀的变形在管体内产生附加应力,膨胀后会残留在套管内部形成残余应力[2-4]。在有限元模型上选择一条路径即z轴向,将模拟计算的结果数据映射到路径上并绘出相关路径图,根据所得数据描绘膨胀后残余应力的分布情况。从图2可以看出,不同膨胀率的膨胀管在膨胀过程中残余应力随轴向的分布情况大体相同,残余应力随膨胀率增加而变大;膨胀过程中残余应力随轴向的分布情况相差很大,通常膨胀锥所在的位置残余应力值较大,膨胀后平均残余应力逐渐减小,应力得到释放。
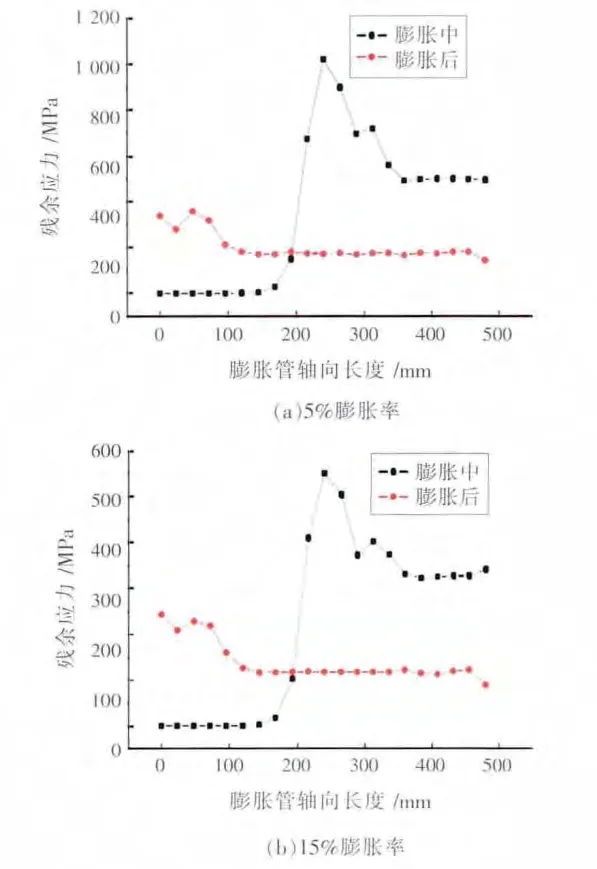
图2 不同膨胀率膨胀过程及胀后残余应力变化示意图
膨胀管的失效方式一般有2种[4],局部挤毁和整体屈服。利用有限元模拟膨胀管局部挤毁和整体屈服状态,并获取膨胀管屈服强度数据。从图3中可以看到,套管挤毁后截面通常变为椭圆形,局部或完全被挤扁。
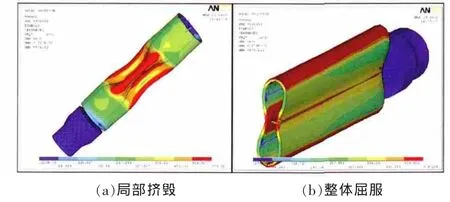
图3 膨胀管失效过程有限元分析
胀后膨胀管屈服强度受到2个因素的影响,一方面塑性变形过程中,膨胀管晶格扭曲、畸变,晶粒产生剪切、滑移,晶粒被拉长[5],表面硬度增加;另一方面由于膨胀管膨胀过程中遵循体积不变原理[6],随着膨胀率的增加,膨胀管壁厚减少,强度降低。
相关试验及有限元模拟分析表明[7-9],随着膨胀率的增加,胀后膨胀管强度逐渐增加,达到峰值后基本保持不变。变化规律如图4所示。
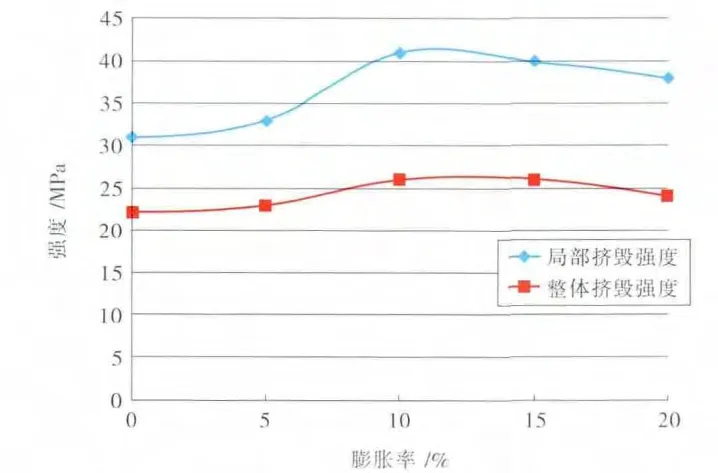
图4 膨胀管屈服失效变化规律
2 膨胀管可靠性模型
膨胀管的塑性变形会导致外径、壁厚不均匀度、椭圆度以及残余应力等参数发生变化,同时由于膨胀率不同,这些参数的变化差异较大。实验与模型计算表明,膨胀管抗外挤强度服从正态分布[8-10]。
2.1 膨胀管抗外挤强度的概率分布
针对膨胀管导致的胀后膨胀管强度变化,利用Klever-Tomano抗外挤强度模型[10-11]作为膨胀管抗外挤失效概率分布函数,其表达式为:
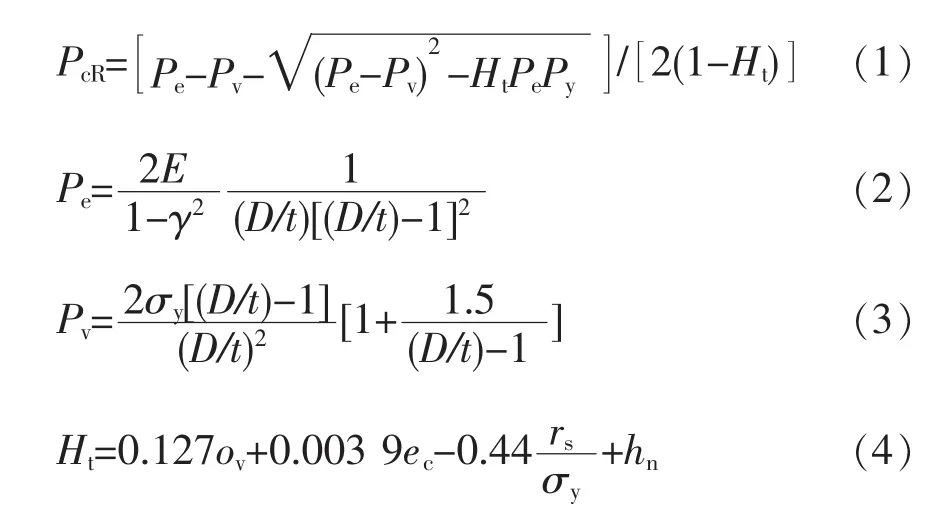
式中:PcR为胀后膨胀管抗外挤强度,MPa;Pe为理想圆管的极限弹性挤毁压力,MPa;Pv为理想圆管的极限屈服挤毁压力,MPa;E为弹性模量,MPa;γ为泊松比;D为膨胀管外径,mm;t为膨胀管壁厚,mm;σy为屈服强度,MPa;ov表示膨胀管椭圆度,mm;ec表示膨胀管壁厚不均匀度,mm;rs为膨胀管残余应力,MPa;hn为膨胀管应力应变曲线形状系数,取值0.009。
2.2 膨胀管抗内压的概率分布
膨胀管抗内压强度有3种表现形式[12-14],屈服强度、塑性破裂强度和裂纹扩展破裂强度。如不考虑腐蚀、氢脆等因素影响,膨胀管在内压作用下的主要失效形式是塑性破裂。研究表明:Klever-Stewart[10,12]提出的塑性变形破坏内压强度模型精度较高,可以作为膨胀管抗外压概率分布函数,表达式为:
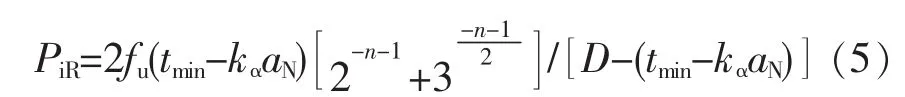
式中:PiR为膨胀管抗内压强度,MPa;fu为膨胀管拉伸屈服强度,MPa;kα为内压屈服系数,取值2.0;aN位膨胀管缺陷深度,mm,通常为5%膨胀管壁厚;n为材料应力应变强度硬化因子,无因次;D为膨胀管外径,mm;tmin为膨胀管最小壁厚,mm。
3 膨胀管安全可靠性评价
根据前面建立的模型计算114mm×7mm规格膨胀管胀后抗外挤和抗内压强度的概率分布,可以得到膨胀管胀后抗外挤和抗内压强度服从正态分布规律,如图5所示。
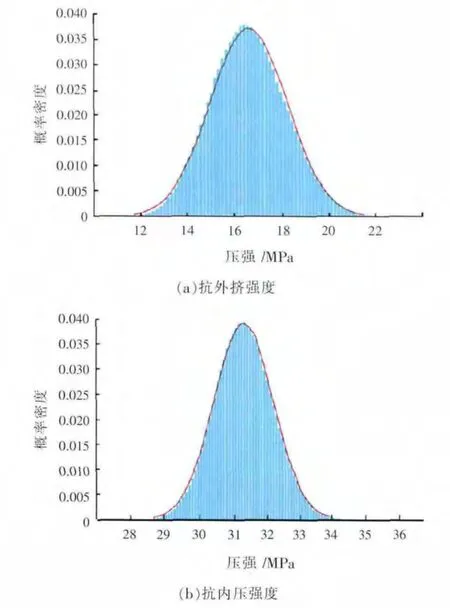
图5 膨胀管胀后强度概率分布
同时利用模型计算不同载荷下膨胀管抗外挤与抗内压的失效概率,如表1所示。结果发现,膨胀管的失效概率与外部载荷并非正相关,不同膨胀率的膨胀管在同一载荷条件下失效概率有较大差异,用可靠性计算的失效概率评价指标可以为膨胀管强度安全系数的科学设计提供依据。
4 结论
1)膨胀管胀后强度受到膨胀率与壁厚变化量双重影响,通常随膨胀率增加变大,达到峰值后基本保持不变。不同膨胀率的实体管在膨胀过程中残余应力随轴向的分布情况大体相同,只是数值大小不同。
2)采用随机抽样法模拟膨胀管强度的随机分布规律,发现受到椭圆度、壁厚不均匀度以及残余应力等因素影响,膨胀管抗外挤与抗内压强度服从正态分布规律。
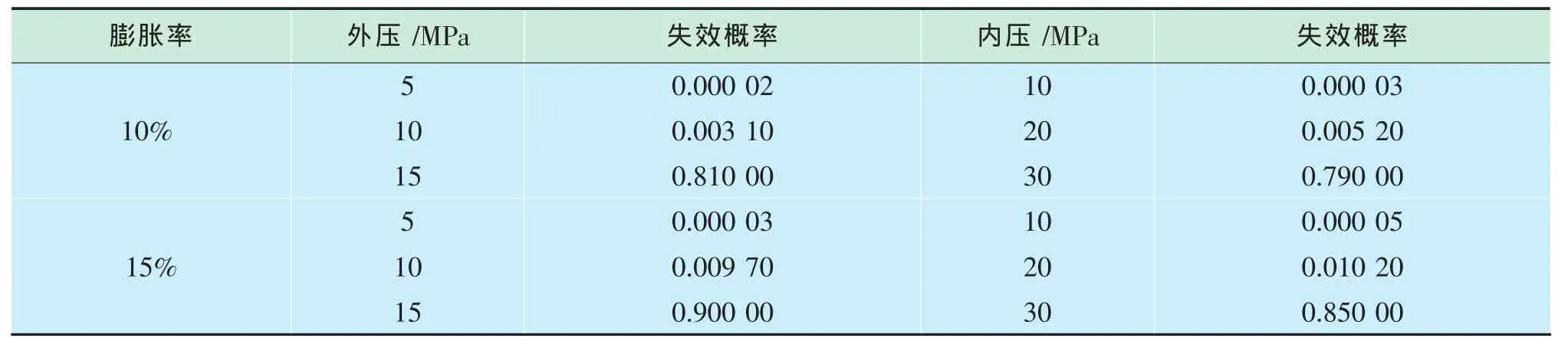
表1 不同膨胀率的膨胀管失效概率与外部载荷数据统计
3)模型计算结果表明不同膨胀率条件的膨胀管失效概率不同,论文研究为膨胀管强度安全系数的科学设计提供依据。
[1]American Petroleum Institute.API Bulletin5C3-1994.Bulletin on formulas and calculations for casing,tubing,drill pipe and line pipe properties[S].Dallas:API Production Department,1994.
[2]张建兵,施太和,练章华.钻井膨胀管膨胀过程中不均匀变形的试验研究[J].石油机械,2004,32(7):1-5.
[3]俞茂宏,何丽南,宋凌宇.双剪应力强度理论及推广[J].中国科学(A),1985,28(12):1113-1120.
[4]Lewis D B.Load and resistance factor design for oil country tubular goods[R].OTC7936,1995.
[5]Cunha J C,Demirdal B,Gui P.Use of quantitative risk analysisfor uncertainty quantification on drilling operations-review and lessons learned[R].SPE94980,2005.
[6]王国荣,刘清友,何霞.套管可靠性寿命预测[J].天然气工业,2002,22(5):53-55.
[7]闫相祯,高进伟,杨秀娟.用可靠性理论解析API套管强度的计算公式[J].石油学报,2007,28(1):122-126.
[8]何水清,王善.结构可靠性分析与设计[M].北京:国防工业出版社,1993:14-20.
[9]王建东,史交齐,林凯,等.套管抗挤强度的可靠性评价方法[J].石油工业技术监督,2005,21(11):36-38.
[10]International Organization for Standardization.ISO/TR10400-2007Petroleum and natural gas industries-equations and calculations for the properties of casing,tubing,drill pipe and line pipe used as casing or tubing[S].Geneva:ISO Copyright Office,2007.
[11]Klever F J,Tamano T.A new OCTG strength equation for collapse under combined loads[R].SPE90904,2006.
[12]Klever F J.Formulas for rupture,necking,and wrinkling for OCTG under combined loads[R].SPE102585,2006.
[13]Adams A J,Parfitt S H L,Reeves T B,et al.Casing system riskanalysis using structural reliability[R].SPE25693,1993.
[14]Liang Q J.Application of quantitative risk analysis to pore pressure and fracture gradient prediction[R].SPE77354,2002.

