GPS高程异常混合模型建模研究

骆丽华，覃 辉

（1.桂林理工大学 测绘地理信息学院，广西 桂林 541004； 2.广西空间信息与测绘重点实验室，广西 桂林541004；3.广东科学技术职业学院，广东 珠海 519090）

GPS测量获得的高程是以WGS84椭球面为基准面的大地高，而在我国工程中采用的高程通常是以似大地水准面为基准面的正常高。因此，在实际测量工作中，大地高和正常高之间的转换就变得十分有意义。通常求取高程异常的方法是通过某种数学模型根据已知的GPS三维坐标模拟求出未知点的高程异常[1]。由于各种单一拟合模型都有其适用条件和使用范围，在一定情况下只使用一种单一模型进行高程拟合很可能会顾此失彼，从而使拟合精度降低。因此研究单一模型如何组合就显得十分有必要。文章通过探究“移去-恢复”法本质[2]，将各种单一模型连接起来，组成混合模型，通过实例验证了它们的可行性。

1 常用的单一拟合模型

1.1 曲面拟合法

二次曲面拟合法[3]的数学模型可表示为：

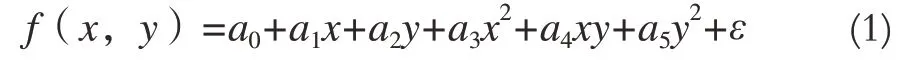
写成矩阵形式有：

式中，

误差方程为：

对于每一个已知点，均可以列出上式方程，在∑ε2=min条件下，可求解系数阵：

再由己知高程异常的权阵情况，式（4）可写为：

系数求出后，再按式（2）求出待求点的正常高。

1.2 多面函数拟合法

多面函数法拟合的数学模型[4]为：

式中，待定系数为ai；核函数Q（x，y，xi，yi）是关于x、y的函数，核函数的中心在（xi，yi）处。理论上核函数是可以任意构造的，在实际应用中，为了简化计算，通常用对称函数，常用的有以下两种。

双曲面：

倒曲面：

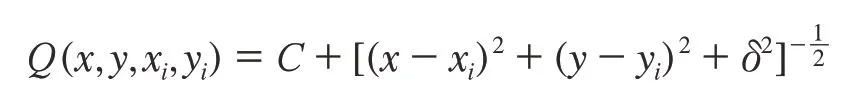
在上述各式中，x，y表示内插点坐标；xi，yi表示已知点的坐标；核函数中的（x-xi）2+（y-yi）2表示内插点到已知点的水平距离；参数δ为光滑系数。

值得注意的是，在选择多面函数求解高程异常值的时候，需要注意光滑系数的选取。为了达到拟合最佳效果，就要逐步地实验改进，然后选定一个最佳值[5]。下文实验中平滑因子值取79 999.112。

1.3 Matlab的Griddata插值函数法

Matlab功能强大、语言自然并且开放性强的特点使其迅速应用到测绘生产中，特别是其丰富的函数库和强大的矩阵处理能力，大大提升了普通测量工程人员的编程效率。Matlab中的Griddata函数可以将位于同一空间坐标系下的散点插值为规则格网，提供了以下4种方法：线性内插法（Linear）、三次多项式内插法（Cubic）、最邻近点内插法（Nearest）和Matlab自带的一种圆滑插值法（V4），可方便地实现结合邻近离散点分布特征的光滑曲面拟合[6]。

1.4 神经网络

BP神经网络结构通常分为输入层、隐含层和输出层，学习过程主要分为正向和反向传播两个阶段[7]。

1）正向阶段。训练时给输入节点随机设置一定的初始权值ω和阈值θ，隐藏层节点j的输入值为：

式中，i、ωi分别为相对于当前层节点j的前一层节点号、权值；θi为阈值。通过激活函数f（x）调整到下一层输入为：

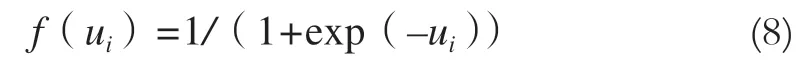
f（x）为标准的Sigmoid函数。f（ui）又作为下一次节点k的输入值，根据权值ωk和阈值θk依次计算k层的输出值。最后传递到输出层的值ξ'l。l=1，2，3，…，n，n为样本数目，至此完成正向阶段的传递。

2）反向阶段。计算实际输出和期望值之间的误差平方和：

根据误差D调整隐藏层上节点的权值和阈值，依次传递回去，到输入层后再开始正向过程。这样通过对权值的不断修改使实际输出与期望输出差值在一定的误差范围内。最后用训练好的神经网络预测测试样本，得到最后的结果。在Matlab下输入向量为点的平面坐标（x，y），目标向量为高程异常ξ，是一种非线性映射[8]，固可用BP神经网络实现。

2 混合模型的构建

2.1 “移去-恢复”法原理

“移去-恢复”法又称为“移去-拟合-恢复”法，一般用“RCR”表示[9]。该方法在利用GPS水准方法拟合测区的高程异常曲面时通常分为3步：首先移去用地球重力模型（EGM96或EGM2008）计算得到的部分，即中长波部分；再用常规拟合方法对剩余部分进行拟合计算，最后在拟合计算的基础上加上利用地球重力模型（EGM96或EGM2008）计算出来的部分，即得到了该点的高程异常值。

通过对“移去-恢复”法的原理进行深入研究后发现，虽然“移去-恢复”法的3种应用的计算过程和方式略有差异，但其本质却是相同的。混合拟合模型就是根据“移去-恢复”法进行改进得到的，具体做法如下：①用常规的单一模型替代地球重力模型等方法求高程异常值，并求出与已知高程异常值的差值；②用另一种模型对差值进行拟合；③将第①步中拟合出来的高程异常加上第②步中拟合出来的差值，得到最终结果。

2.2 模型构建

1）多面函数法 + 二次曲面法。①对测区范围内所有已知点利用多面函数拟合法拟合出各个已知点和未知点的高程异常值。可将大地高和水准高获得的正常高视为高程异常的真值，在已知点上求取高程异常差值。②利用二次曲面拟合法对第①步中的差值进行拟合，求出各个未知点上的残差值。③将第①步中利用多面函数拟合方法求出的未知点的高程异常值与第②步中利用二次曲面拟合法求出的差值相加，得到各未知点的最终高程异常值。

2）BP神经网络法[10]+ 多面函数法。①设区域中有n1个已知点，总的点有n个，则待求点有n2=n-n1。将以上n1个已知点构成学习集样本（xi，yi，ξi），i=1，2，…，n1，其中∆ξi为输出单元参数；xi、yi为输入单元参数。然后利用n1个学习集样本对该BP网络进行训练。用训练好的神经网络对所有点进行计算，并在已知点上求取高程异常偏差。②利用多面函数法对高程异常偏差进行拟合，计算待求点的高程异常偏差。③将BP神经网络计算的待定点与多面函数求取的高程异常相加，得到最终的高程异常值。

同理，以下用到的混合模型如Griddata格网插值法+BP神经网络法、多面函数法+Griddata格网插值法等的构建和计算过程，其本质与以上两种方法类似。

3 实例应用和分析

3.1 数据计算结果

实验是在Matlab7.0环境下进行的。本文数据源于云南某山区区域[11]。区域范围内提出带有明显粗差的点，共布设了24个GPS控制联测点，控制点为三等水准点，GPS网为C级网。图1为24个控制点的点位分布图，其中蓝色被选为拟合点，红色为检核点。

图1 点位分布图

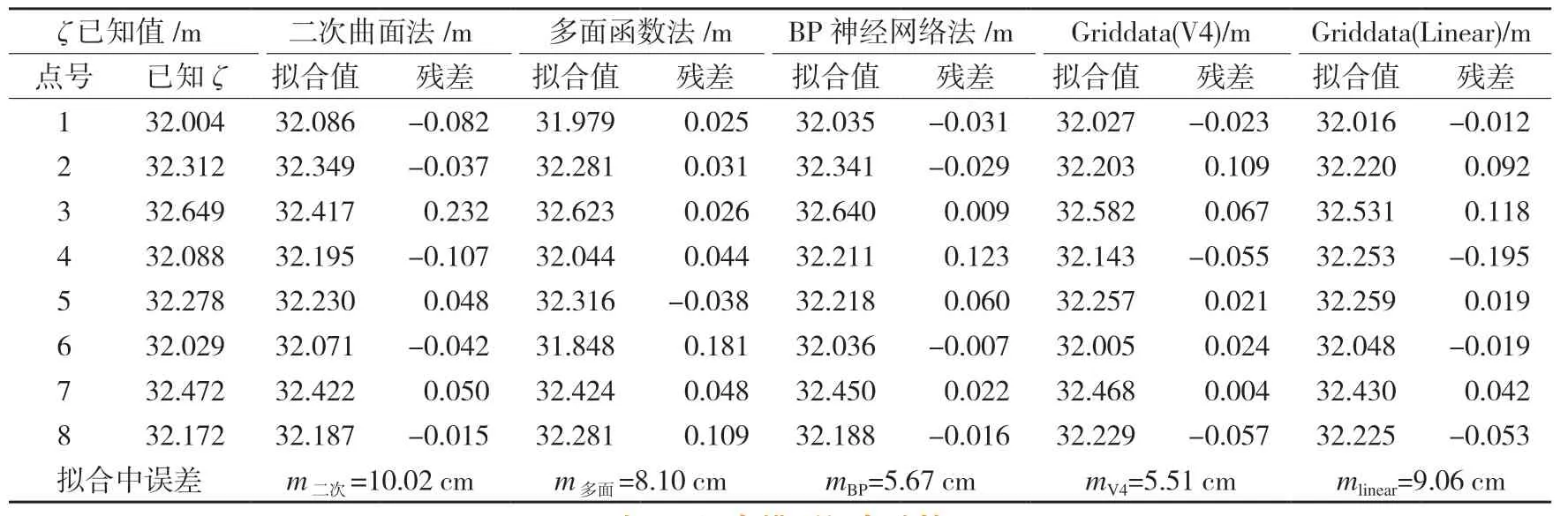
表1 单一模型拟合结果

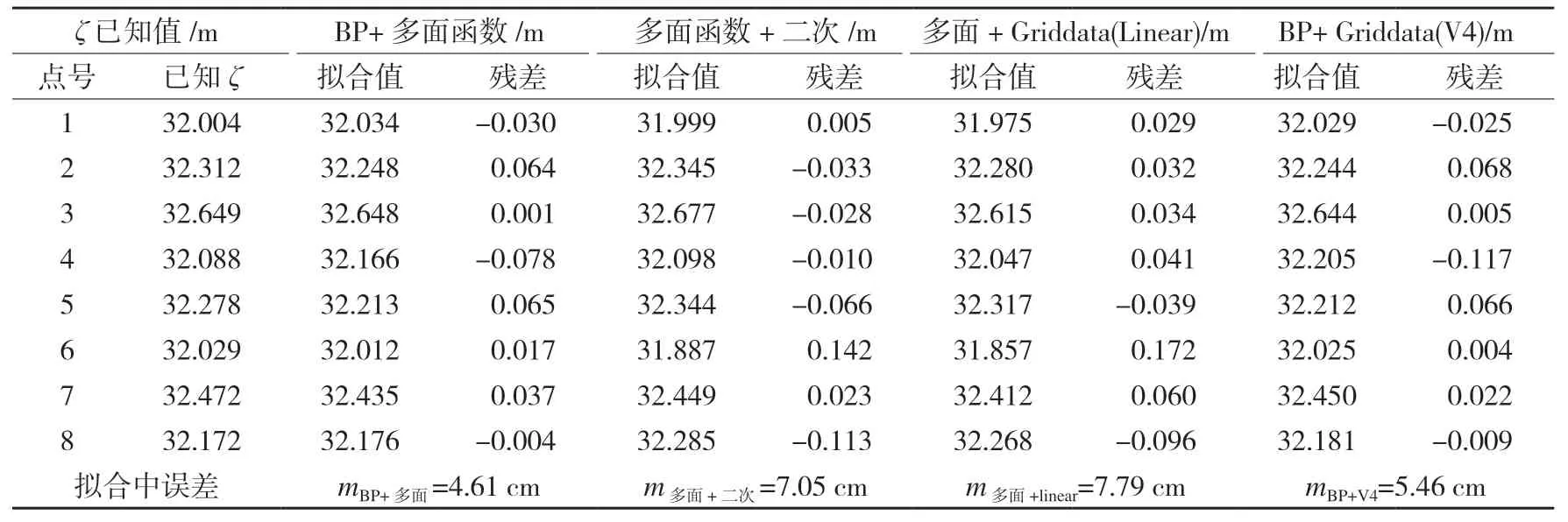
表2 混合模型拟合计算

根据数据，分别利用单一拟合模型和混合拟合模型对其进行实验，拟合计算结果见表1和表2。

3.2 数据精度分析

为了便于观察和计算各拟合模型的拟合结果，同时比较拟合成果间的差异，本文取检核点的单点最大偏差及拟合中误差为评价指标[12]。

图2 单一拟合模型残差对比图

图3 混合拟合模型残差对比图

表3 几种拟合方法的精度对比

由于数据来源于山区地形，高程变化相对较大，拟合效果不理想，精度在cm级。由表3及图2、图3可以看出，单一模型拟合中，二次曲面模型的最大残差为0.232 m，拟合中误差为10.02 cm，误差最大，精度最低；Matlab中Griddata的基于三角形的线性插补法（Linear）最大残差为0.109 m，拟合中误差为5.51 cm，误差最小，精度最高。在混合模型中，多面函数法+Griddata（Linear）混合模型的最大残差为0.172 m，中误差为7.79 cm，精度最低；而BP神经网络+多面函数混合模型最大残差为-0.078 m，中误差为4.61 cm，精度最高。此外本文还用平原地区数据进行实验，由于数据较多，在此不一一列出。

总体来看，无论是平原还是山区，混合模型的精度一般都高于单一的拟合模型，其拟合效果山区地形更为明显，这与分区拟合法有类似效果。混合模型相当于将整个区域进行地形改正来提高精度，而分区拟合则是将区域划分为适合利用其他单一模型的小区域，再通过平滑连接达到更好的拟合效果。较分区拟合法而言，混合模型可省去分区过程，避免区域划分不合理引起的误差以及在平滑连接中繁琐的计算过程，它具有计算简洁、精度可靠、实用性强的特点，能够满足大多数工程的要求。

4 结 语

本文简要介绍GPS高程异常拟合中常用的拟合模型，如二次曲面法、多面函数法、BP神经网络法等，通过探究“移去-恢复”法本质，将各种单一模型进行组合得到混合模型，并用实例进行实验，从中得出了以下有益的结论：混合模型的精度一般高于单一拟合模型精度，且在地势较为复杂的山区效果更为明显，与分区拟合法相比计算过程简洁、精度可靠，在实际应用中更具实用意义；每种拟合模型都有其适用条件和使用范围，在不同区域或不同地形需选择适合的拟合模型，使其达到最好的拟合效果；Matlab自带的Griddata插值函数运用在GPS高程拟合中具有程序编制简便、转换精度可靠的特点。本文根据“移去-恢复”法本质建立的混合模型，验证了混合模型的可用性，为GPS高程拟合提供了新思想。

[1]乔仰文，辛久志，王晓辉.GPS 高程转换的若干问题的研究[J].测绘通报，1999(12):34-35

[2]王爱生，欧吉坤，赵长胜.“移去-拟合-恢复”算法进行高程转换和地形改正计算公式探讨[J].测绘通报，2005(4):5-7

[3]王旭，刘文生.GPS高程拟合方法的研究[J].测绘科学，2010(35):28-31

[4]李秀海，韩冰.基于多面函数模型的GPS高程拟合精度分析[J].测绘与空间地理信息，2010,33(1):12-14

[5]邱斌，朱建军.基于模糊集合理论的GPS高程多面函数拟合模型平滑因子优选[J].测绘工程，2004,13 (3):35-39

[6]陈本富，王贵武，沈慧，等.基于Matlab的数据处理方法在GPS高程拟合中的应用[J].昆明理工大学学报:理工版，2009(5):1-4

[7]Yang Z.Precise Determination of Local Geoid and Its Geophysical Interpretation [J].1999(28):9-11

[8]白征东.Matlab在测量平差教学中的应用[J].测绘通报，2009(11):73-76

[9]李冲，张勤，刘站科.基于CQG2000采用RCR法求解高程异常[J].测绘工程，2002,11(3):31-34

[10]石博强，赵金.Matlab数学计算与工程范例教程[M].上海:中国铁道出版社，2005

[11]黎剑.区域GPS高程异常拟合及建模方法研究[D].昆明:昆明理工大学,2013

[12]杨庆振，郭春喜.多种拟合方法在似大地水准面精化中的比较[J].测绘标准化，2009,25(1):30-32

[13]骆丽华，覃辉.Matlab程序设计在GPS高程拟合中的应用[J].地理空间信息，2015,13(1):99-101