基于集对层次分析法的围岩分类等级研究

王海涛，王素萍

(大连交通大学 土木与安全工程学院，辽宁 大连 116028)*

0 引言

近年来，我国经济飞速发展，地上空间的利用已经不能满足当前经济发展的需求，人们对空间的利用率的逐步提高，地下洞室、隧道开挖等地下工程在城市发展中随处可见.工程施工的安全性问题不容忽视，对于地下工程，特别是地质灾害问题更应引起关注.因此，对围岩的分类等级进行客观、正确的判断对地下洞室、隧道开挖至关重要.

围岩分类等级对地下工程施工至关重要，一直以来都是岩土工程领域研究的热门课题［1］.目前对于隧道围岩分类问题，许多学者作了大量的研究和分析，一些新的理论和方法应用其中，如模糊数学理论［2-4］、灰色关联分析［5］、可拓学［6］、人工神经网络［7-8］等，均取得一定的研究成果，推动了围岩分类等级研究的进展.由于每种理论和方法都有自身的特点，也有一定的局限性，并不能很好地服务于隧道开挖施工，因此对围岩分级方法做进一步的探讨很有必要.

围岩是一个多因素多水平耦合作用的复杂系统，因此对其分级研究具有极大的不确定性［1］.本文结合模糊层次分析法和集对分析法对围岩等级进行评判.主要分为三步:①利用层次分析法求各个评价指标的权重系数;②利用集对分析法求各个评价标准的联系度;③利用加权平均联系度的方法求得最大平均联系度，最大平均联系度所对应的等级即为评价结果.

1 集对分析理论［9］

集对分析理论是1989年我国学者赵克勤提出的，是一种处理系统确定性与不确定性相互作用的数学理论.其基本理论是在一定问题背景下，利用数学运算，对把研究对象作为一个集对，对集对中2个集合的确定性与不确定性和确定性与不确定性的相互作用进行分析，建立两个集合的联系数，借助联系数及其数学表达，将该辩证思想转化为数学运算.利用确定性和不确定行对集对进行具体分析.其中，将确定性称为“同一”和“对立”，将不确定性称为“差异”，从“同一”、“对立”、“差异”三个方面分析整个集对系统，三者之间相互联系、相互影响和制约，同时在一定条件下可以相互转化.在一个集对中，N为特性总数，A为同一特性数，C为对立特性数，则既不相同又不对立的特性数为N-A-C，记为B，“联系数”可用下式表示:

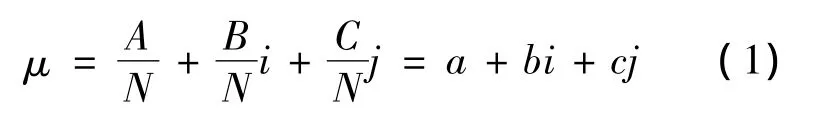
μ为联系度，反映了集对中“同一”、“对立”、“差异”三者的关系;i指三者中“差异”所占的比重，称为差异度系数，一般取［-1，1］;j指三者中“对立”所占的比重，称为对立度系数，一般取-1.其中，i=±1时，表示集对处于“同一”或者“对立”两个确定的极端;i在-1和1之间变化时，表示确定性和不确定性在整个集对中所占的比例.

由于联系度具有可展性，在N个评价指标和多个评价等级中，联系度可由式(1)扩展为下式:

式中:i1，i2，…，im为差异度系数，j为对立度系数.

2 集对——层次分析模型的建立

2.1 层次分析法确定权重系数

用层次分析法确定各评价因子权重系数的步骤如下:

(1)确定评价因子;

(2)根据层次分析法原理，构造判断矩阵.将各层相关指标和因素利用9级标度法(表1所示)进行比较，建立判断矩阵S;

(3)采用式(3)［10］和式(4)处理判断矩阵 S，求得权重值，其中，mij为判断矩阵S中的元素.

表1 9标度法

所得到的 W=［w1，w2，…，wn］T为所求特征向量，即相应因素的权重值.

2.2 联系度的确定

根据集对分析理论对洞室围岩分类进行研究，主要就是确定各个评价指标的联系度.各个评价指标的联系度指标的关系式如式(5)［11］:

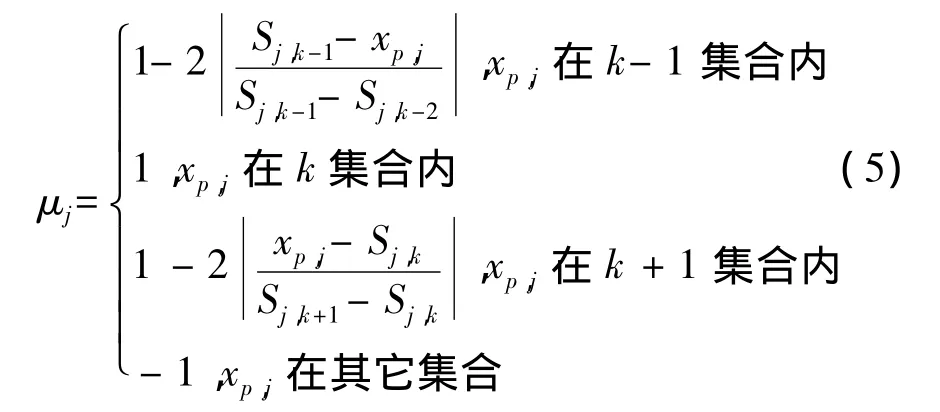
式中:Sj，k-1，Sj，k-2，Sj，k，Sj，k+1，分别为各个评价级别的限定值;x为评价指标j的实测值;μj分别为各评价指标对各指标体系的联系度.

2.3 加权联系度及级别评价的确定

本文采用加权联系度代替平均联系度对围岩评价指标的级别进行评判，即将各个指标的联系度与其相对应的权重相乘，根据最大隶属度原则，取最大联系度作为该评价指标的评价等级.加权联系度的计算公式如下［12］:

3 工程实例分析

3.1 工程背景

本文结合申艳军等［13］用集对分析的可拓学方法对地下洞室围岩分类研究的基础上，采用文中对某大型水电站地下洞室围岩RMR分类的实测数据，建立层次分析法与集对分析法相结合的模型进行围岩分类级别的分析和研究.Rock Mass Rating围岩分级即RMR分级，是毕奥斯基提出的岩石质量评分分类法［14］.RMR围岩分级主要包含五个分类因素:岩石单轴抗压强度σc、岩石质量指标RQD、裂隙间距、裂面特征和地下水状态，其围岩评价等级见表2，实测的洞室围岩RMR各段指标数值见表3.

表2 RMR围岩评价等级标准

表3 各个桩号围岩洞室实测值

3.2 实例计算

3.2.1 层次分析法确定权重

用层次分析法，根据9标度法及其实际工程经验，构建判断矩阵

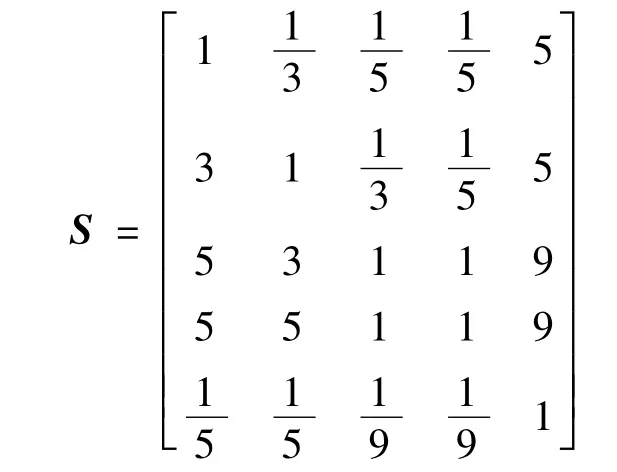
根据式(3)～(4)计算权重.经计算参数指标权重值为:

W=［0.126，0.169，0.313，0.344，0.048］

3.2.2 计算联系度确定评价等级

由于计算过程相同，仅以桩号155～166为例，根据式(5)计算其围岩综合评价等级.结果如表4.根据公式(6)计算加权联系度，桩号155～166 各加权联系度分别为:-0.79，0.63，0.70，-1.15，-1.00.因此，该桩号对Ⅲ级围岩 RMR 分类法的加权联系度最大，故该桩号在围岩分类级别中为Ⅲ级.

表4 桩号155～166各指标相对各等级联系度

按照桩号155～166各级加权联系度的计算方法，对其他桩号进行计算，从而确定各桩号在围岩分类级别中的等级，评价结果见表5.将评价结果和文献［13］相比较，可以看出两种方法结果基本吻合.说明基于层次分析法和集对分析法可以作为研究围岩等级的一种方法.

表5 各等级评价结果

4 结论

本文采用文献［13］中RMR分类法实测围岩洞室的数据，用层次分析法建立分析模型，计算各个评价指标的权重;基于集对分析法的原理，通过联系度来描述各个评价指标的确定和不确定性;用加权联系度判断指标分类等级.计算评价结果与其他分析方法计算基本吻合，可见此方法可以用与对洞室围岩分类等级的评价判断.应用实例表明:

(1)利用集对分析理论，能较好处理确定和不确定性问题，而层次分析法用定量和定性分析相结合的方法处理问题，两者相结合，计算过程简单，结果可靠，可以作为研究围岩等级的一种新方法;

(2)采用RMR围岩分类方法，结合实际工程确定岩石单轴抗压强度σc、岩石质量指标RQD、裂隙间距、裂面特征和地下水状态的参数，建立围岩分类等级的评价体系;

(3)结合大量工程实践，采用9标度法，构造RMR法各评价因素指标的判断矩阵，得到各指标的权重 W=［0.126，0.169，0.313，0.344，0.048］;

(4)基于集对分析法的原理，结合层次分析法确定的权重值，用加权联系度和最大隶属度原则判断指标的类型.计算过程简单，结果和文献［13］结果基本吻合，可以作为研究围岩等级的新方法.

［1］王迎超，徐兴华，刘永莉，等.公路隧道围岩分级的集对分析模型［J］.哈尔滨工业大学学报，2011(4):114-119.

［2］许传华，任青文.地下工程围岩稳定性的模糊综合评判法［J］.岩石力学与工程学报，2004，23(11):1852-1855.

［3］王迎超，严细水，胡建平，等.隧道围岩模糊分类研究［J］.华东公路，2007(5):53-57.

［4］HUO R K，LIU H D.An application of neural network to surrounding rock stability classification［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，1998，19(2):62-63.

［5］陈志波，简文彬.边坡稳定性影响因素敏感性灰色关联分析［J］.防灾减灾工程学报，2006(4):473-477.

［6］连建发，慎乃齐，张杰坤.基于可拓方法的地下工程围岩评价研究［J］.岩石力学与工程学报，2004，23(9):1450-1453.

［7］周翠英，张亮，黄显艺.基于改进BP网络算法的隧洞围岩分类［J］.中国地质大学学报:地球科学版，2005，30(4):480-486.

［8］邱道宏，陈剑平，金声，等.基于粗糙集和人工神经网络的洞室岩体质量评价［J］.吉林大学学报:地球科学版，2008，38(1):86-91.

［9］赵克勤.集对分析及其初步应用［M］.杭州:浙江科技出版社，2000.

［10］桂黄宝，赵付民.基于模糊层次分析法(FAHP)的合作技术创新伙伴选择研究［J］.科学学与科学技术管理，2007(9):50-54.

［11］孟成才.基于集对分析-可变模糊集的地表水环境质量综合评价［J］.安徽农业科学，2010，38(22):11897-11899，12046.

［12］李培月，吴健华.熵权集对分析法在地下水水质评价中的应用［J］.宁夏工程技术，2010(1):64-67.

［13］申艳军，徐光黎，张亚飞，等.基于集对分析的可拓学方法在地下洞室围岩分类中的应用［J］.地质科技情报，2010(5):125-130.

［14］BIENIAWSKI Z T.Engineering Rock Mass Classification［M］.New York:Wiley，1989.