非线性扩散作用下一类四阶抛物方程解研究

梁 波，沈慧颖

(大连交通大学 理学院，辽宁 大连 116028)*

非线性四阶抛物方程的研究最近受到关注，形如ut+(upuxxx)x=0及=0的类型的方程可用来描述非常薄的粘性可压缩流体沿着斜面运动的情况，其中未知函数u代表流体薄层的的厚度(可参考文献［1-2］).Bernis等人［3］在分数次连续函数空间中证得了弱解的存在性.文献［4-5］还对解的长时间行为等问题进行了研究.

本文主要研究一类带有非线性二阶扩散项的四阶抛物方程，形式如下:

这里Ω是RN中的一个有界开区域，QT=Ω×(0，T)，Γ=∂Ω × (0，T)，∂Ω∈C1，p ＞ 1，m≥0.为叙述方便，下面引入两个符号定义:

利用半离散方法可得到解的存在性如下:

定理1(存在性) 方程(1)～(3)存在弱解满足:

(1)ut∈Lp'(0，T;W0-1，p'(Ω))，u ∈ L∞(0，T;H10(Ω))∩C([0，T];L2(Ω))，Δu∈Lp(0，T;W10，p(Ω))，Δu∈ Lm+2(QT);

(2)对任意的φ∈C∞0(QT)，有

利用检验函数法可获得解的唯一性定理:

定理2(唯一性)(1)～(3)的解是唯一的.

1 定态解的存在性

本节来研究对应的定态问题:

定义泛函

其中，φ∈C∞0(Ω)为任一检验函数.

0 引言

由下确界定义，存在子列 { uk}∞k=1⊂ B，使得I[ uk]→vinBf[v] ，(k → ∞).所以 ‖▽Δuk‖LP(Ω)∈≤ C ，‖Δuk‖Lm+1(Ω)≤ C .利用 Poincare不等式及二阶椭圆方程的Lp-估计，可得

所以，存在 {uk}的一个子列及u∈B，使得

uk→弱u于W1，p0(Ω)∩W2，p(Ω)，

Δuk→弱Δu于W1，p0(Ω)，

Δuk→弱Δu于Lm+1(Ω).

2 抛物问题的存在性

考虑离散问题如下

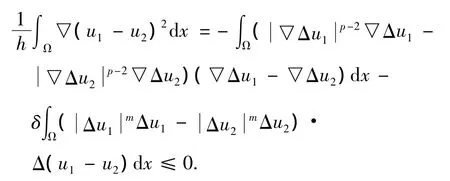
为证明定理1，以(7)～(8)为基础定义近似解如下

χk(t)是时间区间 ((k-1)h，kh］，k=1，2，……，n上的特征函数，为获得逼近解的收敛性，我们需要一些一致估计.

引理2 对于近似解(9)，下面的正则估计成立证明 类似参考文献［6］的证明思路，以Δuk为(7)～(8)的检验函数，并利用(9)易知因 此 ‖▽w(n)‖L∞(0，T;L2(Ω))≤ C.同 时 可 知.其余估计类似文献［6］，得证.

定义第二类近似解如下

这里

对此近似解有如下估计.

引理3 下面的一致估计成立，

证明 由于

对任意的 φ ∈ w1，p0(Ω)及 ‖φ‖w1，p0(Ω)≤1 ，由(10)可知

其中α和β为某正指数.根据u(n)的定义

定理1的证明:根据能量估计(10)，存在w(n)的一个子列及泛函v，使得当n→∞ 时

存在足够大的整数r＞0，使得w-1，p'(Ω)→H-r(Ω).由Aubin'sLemma［7］，嵌入H10(Ω)→紧L2(Ω)→H-r(Ω)及一致估计(12)，则u(n)存在子列使得当n→∞时

利用u(n)和w(n)的定义可知，对于任意的φ∈C∞0(QT)，

因此ρ=u a.e于QT中.

对任意的检验函数φ，有

令n→∞得到

另一方面，

注意到

取ζ(n)=▽Δw(n)，ηε=▽Δ(u-εφ)(对于任意的φ及ε＞0)，由(15)～(16)知当n→∞ 时

再由(14)得

当ε→0时，得到

利用φ的任意性可知 ▽Δup-2▽Δu=v几乎处处于QT.唯一性容易证明，这里省略.

［1］CAHN J M，HILLIARD J E.Free energy of a non-uniform system I，Interfacial free energy［J］.J.Chem.Phys，1958，28:258-367.

［2］MYERS T G.Thin films with high surface tension［J］.SIAM Rev，1998，40:441-462.

［3］BERNIS F，FRIEDMAN A.Higher order nonliear degenerate parabolic equations［J］.J.Differential Equations，1990，83:179-206.

［4］CARLEN E A，ULUSOY S.An entropy dissipation estimate for a thin film type equation ［J］.Commun.Math.Sci，2005(3):171-178.

［5］KING JR.Two generalization of the thin film equation［J］.Math.Comput.Modelling，2001，34:737-756.

［6］LIANG B，ZHENG S.Existence and asymptotic behavior of solutions to a nonliear parabolic equation of fourth order［J］.J.Math.Anal.Appl.，2008，348:234-243.

［7］SIMON J.Compact sets in the spaceLp(0，T;B)［J］.Ann.Mat.Pura appl.，1987，146:65-96.