逆向物流累积批量处理模式下旅游产品销售商的最优库存控制模型

李 冰

（唐山师范学院，河北 唐山 063000）

1 引言

近些年来，随着物流产业的迅速发展，供应链管理所发挥的作用也日益重要。供应链是由多个相关环节构成的网络系统，该系统能够整合优势资源以增强企业的综合竞争力，进而提高企业的整体效益。传统研究多注重研究供应链管理的模式等，很少涉及供应链管理中的逆向物流。其实，逆向物流是供应链管理中非常重要的一个环节。其具体是指由于多种因素导致的、需要回收产品引致的逆向物流活动，一般来说包含产品的回收、检测、维修、再利用等多个环节。逆向物流流程如图1所示。

图1 逆向物流流程图

在逆向物流的发展过程中，库存控制是其研究的重点，现已取得了相当多的研究成果。但是大部分研究都集中在如何使库存成本较小等方面，与实际情况差异较大。实际上，销售商会考虑其企业形象等问题，从而通常会对回收后的产品进行必要的处理。鉴于此，本文以旅游产品逆向物流为研究视角，以对退回的旅游产品进行累积批量处理为前提，构建了最优库存控制模型。

2 模型建立

本文所研究的库存控制模型仅针对一种产品进行，具体如图2所示。

图2 含有逆向物流的销售单一产品的库存控制模型

为方便研究，本文假设当顾客购买产品后，在一个订货周期内提出退货要求，而销售商同意其退换要求，同时该顾客退货与否和其对产品的需求没有直接关系。另外，其服从泊松分布。用T表示处理退回产品的周期，而一个订货周期则指销售商连续两次接受订货的时间差，因此，可以分析出处理退回产品的周期与订货周期之间的关系，即后者是前者的倍数，可以用nT表示产品的订货周期。由于本文研究的是销售商对旅游产品逆向物流累积批量处理模式，在确定销售商的最优订货数量和订货周期时，不考虑顾客对产品在某一时刻的需求对后期退货的影响。

2.1 模型假设

由于顾客的购买需求与退货没有直接关系，因此，设其购买需求服从泊松分布，并用d表示其参数；而其退货情况也服从泊松分布，用λ表示其参数，且λ＜d；假设不会出现缺货情况，当储存量为零时，能够立即补充产品；销售商可以自己修理其被退货的产品，若不考虑修理时间，则可以打折销售修理后的产品，用α表示打折系数，且α＜1，同时该情况不对顾客的需求分布造成影响。

设订货一次的固定成本用C0表示，而对退回产品进行批量修理所需固定成本用Cf表示，修理单位退回产品的成本用Cr表示；单位时间内存储单位数量产品所需的成本用hs表示，单位时间内存储单位数量的退回产品的成本则hr表示；购买单位产品的价格用K表示；在t时刻储存产品的水平用I(t)表示；退回产品j的到达时间用Xj表示。

分析模型假设可以看出，在单位时间内，顾客的购买需求大于其所退回产品的平均值，反之，顾客的退货则会覆盖其购买需求。在第二种情况下，可以采用处理库存产品的方法。因此可以得出：E[Xj] =j λ。

2.2 模型建立

每当退回的产品累积到一定数量，就集中处理1次，这就叫做“累积批量处理”。尽管处理退回的产品的批量大小确定，但产品数量不定，因此处理时间是一个随机变量。以单位时间内总成本最小为目标，对订货数量Q以及退回产品的累积处理批量Qr进行计算，是对其进行优化的首要任务。

总成本包含以下四部分：

（1）库存成本（整个订货周期）。通过设计模型的库存特点可知：

其中，Tj表示处理第j次退回产品的结束时间，T0=0。

退回产品数量累计到Qr时方可进行集中处理，其中，间隔的 时 间 用 Δt表 示，且 ΔT=Tj-Tj-1=Qr/λ，进 而Tj=jQr/λ(j=1,2,…,n)。通过假设条件可知，不存在缺货的情况，若储存量为零，立即补充产品，因此可知，I(Tn)=0。处理第n次 退 回 产 品 的 结 束 时 间 用n λ表 示，所 以Q=(nd/λ-n+1)Qr,整个订货周期库存成本Coi的期望值为：

（2）储存退回产品的成本。由ΔT=Tj-Tj-1=Qr/λ、E[Xj] =j/λ，且退回产品数量需累计到Qr时才能进行集中处理可知，其储存成本Crp的期望值为：

在订货周期内，储存等待进行修理的退回产品成本用Cri表示，其期望值为:

（3）对退回产品进行修理的成本。在订货周期内，修理退回产品的成本用Crri表示，其期望值为：

当退回产品数量累积到Qr的修理成本用Crr表示，其期望值为：

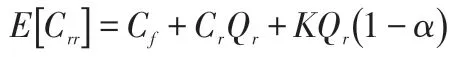
（4）订购货物的成本。订购货物的成本用Co表示，其期望值为：

最后可得，在整个订货周期内的期望总成本为:

式（1）对(Qr,n)求极小值的一阶条件分别是：

假设Qr和n为连续变量，通过以下定理可以求出使C(Qr,n)最小的Qr和n。

证明：根据已知理论，只需要证明C(Qr,n)是严格凸函数。已知C(Qr,n)的海塞矩阵为：

首先把式（4）代入式（5）中，利用数值计算法求解；最后再利用式（4）求n*值。

3 实例分析

为验证模型的有效性，本文对北京颐和园旅游景点处销售的一种旅游纪念吊坠进行实例分析。假设此种旅游纪念吊坠的外部参数为：吊坠的订购单价为20元，即K=20元/件；顾客对吊坠的购买需求服从泊松分布，且其参数为d=18；而其退货也服从泊松分布，且其参数为λ=4。d和λ的值取自大量观测数据的平均值；修理后吊坠打九折，即其打折系数α=0.9，每次订货的固定成本为100 元，即C0=100元/次，对退回吊坠进行批量修理的固定成本为15 元，即Cf=15元/次；修理退回吊坠的单位成本为2 元，即Cr=2元/件；储存吊坠一个月的成本为4 元，即hs=4元/（件·月）；储存退回吊坠一个月的成本为3元，即hr=3元/（件·月）。

通过本文构建的模型可知，只有当顾客退回吊坠达到一定数量时，销售商才会对其进行集中处理。根据前文模型部分的公式计算可知，只有当顾客退回吊坠的数量累积到3 件时，销售商才会对其进行集中处理。通过退回吊坠的数量变化导致的成本变化可知，吊坠的参数变化会对其最优策略造成一定的影响，因此本文对不同参数进行了大量的数值分析，当吊坠任一参数发生变化，而其他参数保持不变时，具体结果见表1。

通过分析表1可知，当λ=1 时，订货成本C(Qr,n)=529；而当λ=7 时，订货成本C(Qr,n)=443，可见，加强商品退货强度λ会使商品的订货成本降低；同理λ增大时，n的值也会增大。通过分析表1以及各成本推导公式可得出以下结论，一方面，随着商品退货强度的增加，其商品订货周期会延长，而订货成本则会在一定程度上降低；另一方面，增大商品的d、C0、Cf、K、hs，订货成本C(Qr,n)会随之增大。

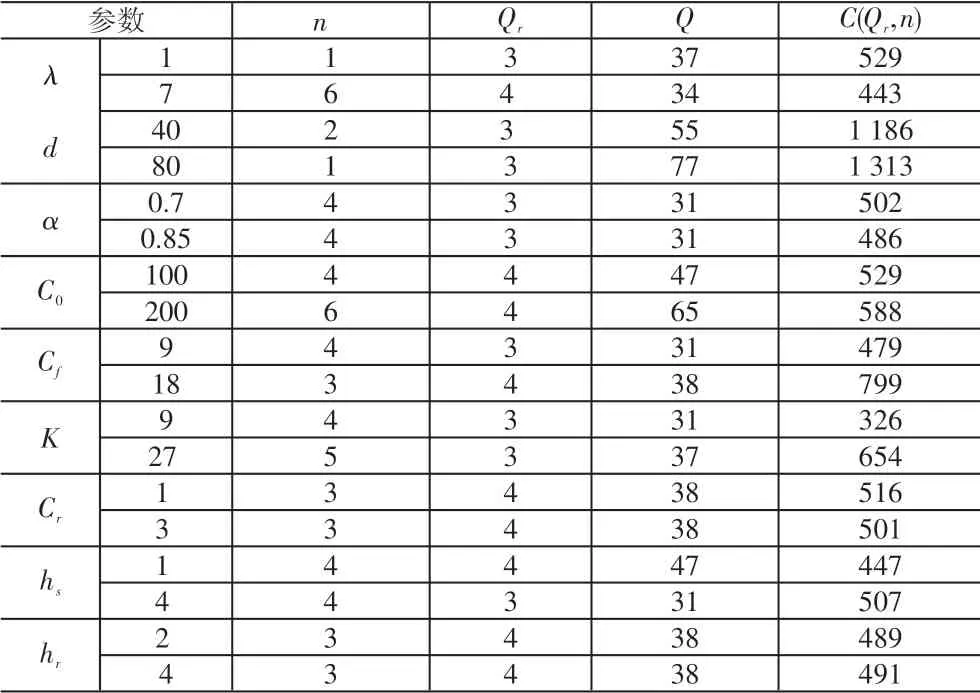
表1 参数变化对最优策略的影响

4 结论

本文主要研究了退回产品累积批量处理方式下，旅游产品销售商采用的最优库存控制模型。在现实生活中发生退回产品的概率较小，因此，退回产品的数量较少，其等待处理的时间不长,致使处理批量Qr也不大，进而无法体现累积批量处理的规模效益。事实上，根据产品的不同情况，销售商可以采用不同的处理方式。受限于篇幅，本文未考虑销售商面对多种产品随机退货以及生产商的补货受生产能力制约等情况，将生产商考虑到逆向物流网络结构中，如何制定相应的订货策略等方面，将是未来的研究方向。

[1]何学容,吴卫.东风汽车销售物流渠道实例研究分析[J].物流技术(装备版),2013,(10).

[2]陈道志.电子商务环境下物流服务与支付意愿的实证研究—以北京生鲜产品销售为例[J].物流技术,2013,(11).

[3]张亚佩.基于BP神经网络的整车物流销售模型的统计和预测研究[J].物流技术,2013,(11).

[4]任鹏,邓书显.包含逆向物流的库存控制模型研究[J].西华大学学报(自然科学版),2010,(7).

[5]农毅,张西莎.我国废旧家电逆向物流体系文献综述研究[J].物流科技,2013,(6).