基于SFA法的集装箱港口效率比较研究

艾亚钊，周坤晓

（1.东莞职业技术学院 物流工程系，广东 东莞 523808；2.东莞理工学院 计算机学院，广东 东莞 523808）

1 引言

国内外港口效率多指标评价通常使用货物吞吐量、港口服务水平、船舶机具的数量、船舶工作效率、岸线长度、职工人数、固定资产原值平均余额等指标，评价的方法主要集中在数据包络分析法（Data Envelopment Analysis, DEA）和随机前沿生产函数法（Stochastic Frontier Analysis, SFA），并且把港口效率细分为技术效率、配置效率、规模效率等。如Liu[1]以英国28个港口为研究对象，以人均工资、账面固定资产为投入指标，总吞吐量为产出指标，利用SFA 法计算技术效率。Tongzon[2]借助DEA法，以起重机数量、集装箱泊位数量、拖船数量、堆场面积、船舶等待时间等为投入指标，以货物吞吐量、船舶工作效率为产出指标，对亚洲4 个和其它地区12 个国际港口效率进行比较研究。

国内文献对港口投入指标的选取分两类：一类是财务数据指标，选用总资产、员工人数、主营业务成本、流通股数等作为投入指标。如罗俊浩[3]、黄勇[4]等，这种方法的优点是可以良好地反映港口资本的经营效率，缺点是将复杂的港口生产变量都归结到资金这一指标上，具有片面性；第二类是港口生产指标，选用基础设施和机械设备数量，如码头长度、码头面积、码头集装箱货运站（Container Freight Station, CFS）数、桥吊数、前沿水深等指标，如匡海波[5]、张小蒂[6]、刘大熔[7]、陈春芳[8]等。第二类指标更能反映港口复杂的生产状况，因此被广泛采用。

自20世纪90年代以来，我国集装箱港口的生产条件和权益结构发生了巨大变化。国内文献在选取指标时，除了刘大熔教授于1994年将财务数据指标和港口生产指标共同作为投入指标，利用DEA 法和因子分析模型（Factor Analysis Model，FA）实证分析港口产出和效率之外，极少有文献将两类指标共同作为投入指标分析港口效率。本文尝试利用SFA 法，并综合采用两类指标作为集装箱港口投入，分析港口效率。

需要指出的是，SFA法能够克服DEA法的局限，充分考虑统计噪音，并对外部影响因素建模。

2 基于SFA 的技术效率（Technical Efficiency, TE）模型

SFA生产函数模型由Aigner、Lovell与Schmidt、Meeusen与Broeck、Battese与Corra等于1977年分别提出，SFA在确定性生产函数的基础上，提出了具有复合扰动项的随机边界模型。其基本表达形式为：

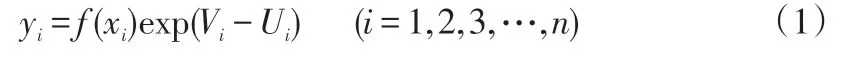
其中xi，yi为生产单位i的投入和产出观测值，f(xi)为生产单位i的可能最大生产技术水平，Vi为统计噪音，即随机误差项，是企业不能控制的影响因素，具有随机性，用以计算系统非效率，Vi服从正态分布，Vi～N(0,σ2v)。Ui为非负随机变量，是技术损失误差项，是企业可以控制的影响因素，可用来计算技术无效率。Ui相互独立且服从相同的分布，常用的分布有四种：半正态分布、截断正态分布、指数分布和伽马分布，它们都是单边分布，Vi和Ui相互独立。

SFA模型由两部分构成：（1）确定性函数部分，（2）随机变量部分。

常用的确定性函数有：柯布道格拉斯函数（Cobb-dauglas）、超越对数函数（Translog）、广义列昂惕夫函数（Leontief）、固定替代弹性函数（CES）等。其中Translog函数为：

Translog函数可以看做Cobb-dauglas函数加上另外一个非线性交叉变量函数，该非线性交叉变量函数具有非常高的替代弹性，由于可以用二次近似法求解未知形式的二次连续可微函数，可以把超越对数函数描述成二阶泰勒级数展开式，也就是说，Translog 是泛化了的Cobb-dauglas 函数，Cobb-dauglas函数是Translog的特例。由于Translog可以灵活的计算随机前沿面，替代弹性强，因此在可用数据不充分的情况下，可以使用Translog函数计算效率模型中的确定性部分。

对于随机变量部分，Battese和Coelli于1992年提出了随机项Ui服从截断正态分布的纯效率模型，适用于时间数列上的面板数据：

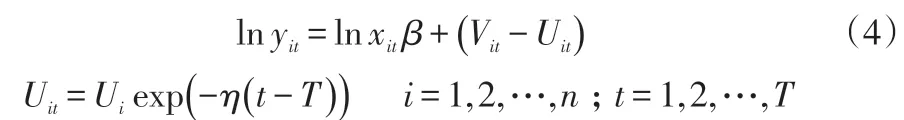
其中：yit为第i企业在第t期的产出向量；xit为第i企业在第t期的投入向量；β为参数向量；Vit为随机误差，服从独立同分布，Vitiid～N(0,σ2v)，与Uit相互独立；η为标量参数；Uit为技术无效率项，独立同分布于非负的截断正态分布，Uitiid～N(mit,σ2u)。

Battese 和Coelli 于1995 年提出了适用于面板数据的全效率模型[9]，考虑了外部因素对无效率分布的影响：

其中：yit、xit、β、Vit的含义与式（4）相同；Uit为技术无效率项，由多个无效率因素组成，独立同分布于非负的截断正态分布，为影响效率的外生变量向量；δ为参数向量。

式（4）为纯效率模型，即确定性生产函数部分包含了外生变量，外生变量与投入指标一起既影响产出又影响效率。

式（5）为全效率模型，即外生变量包含在随机无效率项中，而不是包含在确定性生产函数中，外生变量只影响效率不影响产出。

通过对纯效率和全效率的比较可以分析出影响效率和产出的因素。利用Translog 形式表达的面向产出的技术效率模型为：

技术效率可用公式表述为：

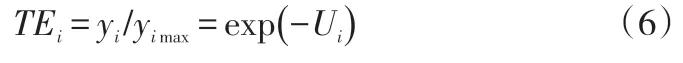
3 指标选取

鉴于我国集装箱港口的生产条件、权益结构和我国劳动力价值的提升，为了作出较全面的效率分析，综合财务指标和生产指标，可以把集装箱港口的投入指标分为4类：（1）基础设施：选用码头前沿维护水深（港口对外公布的通航水深）x1和码头前沿岸线长度x2；（2）机械设备：选用港口桥吊数量与龙门吊数量之和x3；（3）劳动力：选用职工总人数（在职人员数与离退休人员数之和）x4；（4）运营资本：考虑到数据的可得性，选用当年统计的资产总额x5。

产出指标y 用年集装箱吞吐量（TEU）表示。选取经济腹地进出口贸易总额z 作为影响码头效率的外部因素。该指标不能直接作为投入要素，但是影响产出，不同的腹地经济状况反映不同的市场需求，从而导致港口产出的不同。本文选取的全部指标见表1。

表1 集装箱码头技术效率评价指标

4 实证研究

4.1 指标分析

本文选取珠三角深圳港集装箱港区（盐田码头、蛇口码头、赤湾码头和大铲湾码头）、虎门港集装箱港区、广州港集装箱港区（黄埔码头、新沙码头和南沙码头）、中山港集装箱港区、珠海港集装箱港区共5个港口的集装箱港区数据进行分析（原始数据来源于各港口官网、统计年鉴和各公司年报）。面板数据选用2007-2012 年的数据，截面数据选用2012 年的数据，对原始数据进行的描述性统计见表2。

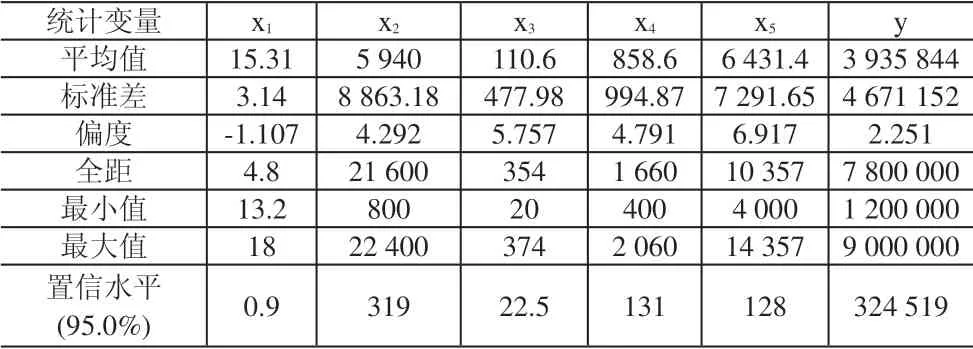
表2 5港口原始数据的描述性统计（2012年）

可以看出，港口前沿维护水深x1表现为负的偏离，其它指标均为正偏离，说明整个样本的港口前沿维护水深呈现左偏离，即深水港多，浅水港少，且偏斜的程度较小。而表现为正偏离的指标说明与整个样本的范围相比，多数港口属于小规模港口（除盐田港和蛇口港外，其它规模均较小）。为了更详细说明指标值之间关联程度，计算指标相关性（见表3）和R平方值（见表4）。

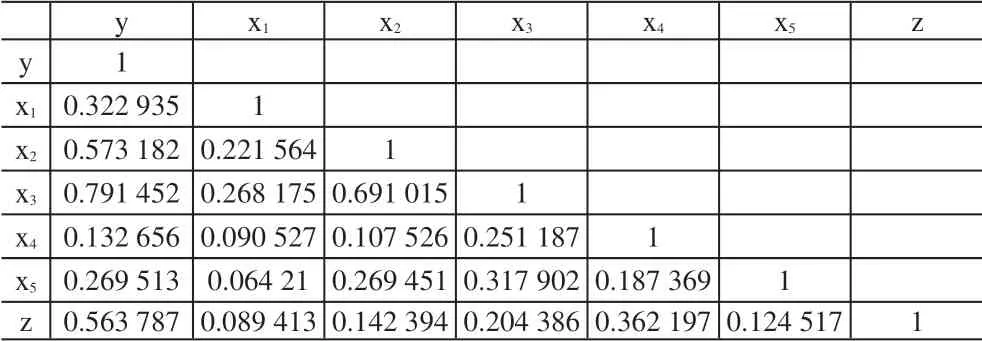
表3 变量之间相关性分析

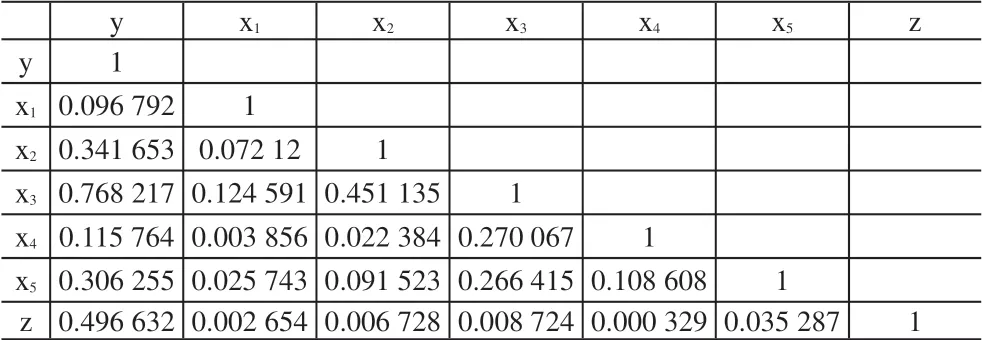
表4 变量之间R平方值分析

岸线长度x2、码头机械数x3和腹地进出口贸易总额z与产出y具有较强相关性，而x3与x2、x4、x5的关联度均在0.5以上，且与y 的关联度接近0.8，说明了港口机械设备数对港口产出有至关重要的影响，说明了码头的基础设施和机械设备之间存在同步增减的规律，即大型码头的机械多、小型码头需要的机械少。同时，港口机械数多意味着集装箱处理能力强，对港口机械设备的管理和调度应成为港口生产管理工作的重中之重。腹地进出口贸易总额这一外部影响因素z 与产出y 正相关，且有超过0.5的关联度，说明腹地进出口贸易越活跃，港口产出越大，国际贸易量与集装箱运量呈正比例关系。需要指出的是，x4与x3、x5的关联度高于其与其它指标的关联度，且x4与所有指标的关联度均在0.4以下，说明职工人数的多少与集装箱港口的产出之间的关系并不密切，但其与港口资产总额和机械设备数有弱关联，这可以用集装箱港口的资本密集型产业性质和信息化技术的应用来解释。

4.2 模型估计结果分析

外生变量在纯效率模型中同时影响效率和产出，而在全效率模型中只影响效率而不影响产出。因此，通过对纯效率和全效率的比较可以分析出影响效率和产出的因素。下面通过比较全效率模型和纯效率模型的参数估计，深入分析外生变量对效率和产出的影响程度。使用FRONTIER 4.1程序，采用极大似然估计法（Maximum Likelihood Estimation, MLE）估计参数。结果见表5。

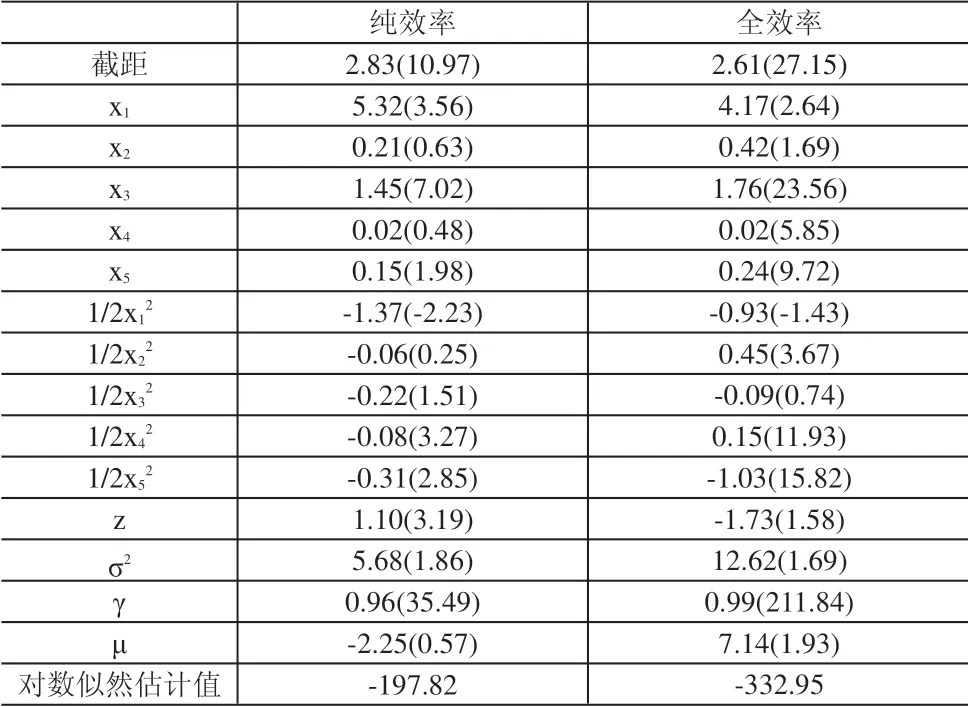
表5 估计结果

估计结果表明：

（1）表5 中γ值趋近于1，表明外生变量腹地进出口贸易总额z直接影响效率，而非通过影响生产技术间接影响生产效率。z在纯效率模型表现为正值，结合前面的分析可知，z在纯效率模型中与其它指标一起同时影响产出和效率，且z与其它指标正相关，z的增减导致产出和效率的同步增减，即z强化了产出和效率值。而z在全效率模型中的表现为负值，这意味着将z从纯效率模型的确定性函数中剥离后，作为随机扰动项影响效率，那么z 值的增加和减少，会分别导致效率的降低和提高。这说明港口腹地进出口贸易总额对港口效率起正强化作用。

（2）所有指标中，前沿水深x1、岸线长度x2、港口机械数x3、职工人数x4、资产总额x5均表现为正值，说明水越深、港口越大、机械数量越多，职工人数越多、产出越大，资金占用额越大，这符合我们的正常期望。表5中反映出的全部指标在样本均值点的产出弹性系数值中，x1和x3的产出弹性系数值较大，1%的水深增加导致5.32%的产出增加，1%的机械数量增加导致1.45%的产出增加。x4和x5的产出弹性系数值较小，1%的职工人数增加导致0.02%的产出增加，1%的资产总额增加导致0.15%的产出增加。可以得出2个结论：一是职工人数的多少对产出的影响微弱，在不影响正常经营的条件下，降低职工人数不影响产出；二是水深条件和港口机械数量对集装箱港口至关重要，水深与地理位置有关，而集装箱港口机械化、提高港口整体作业能力，是提高集装箱港口产出的主要因素。

（3）对于资产总额x5，1%的资产总额增加导致0.15%的产出增加，说明珠三角集装箱港口在总体上处于资金回报率降低阶段，即港口规模报酬递减，也即港口作业能力大于市场需求。有两个原因：一是2008 年至2012 年全球金融危机持续，珠三角港口腹地进出口贸易跌至谷底后，复苏乏力，集装箱运量减少；二是2008年以前，港口航运业的经营业绩一贯良好，基于对未来行业发展极端乐观的判断，各地掀起了集装箱港口建设的高潮，新建和扩建项目纷纷上马，导致产能过剩。如2010 年深圳新建成大铲湾集装箱港区，2008 年广州南沙集装箱港二期投入使用，珠海高栏港二期3、4 号泊位2012 年投入使用等。

5 效率分析

选取2007-2012年的面板数据，计算出时间序列上的集装箱码头的纯效率值和全效率值（见表6）。

表6 港口效率指标值

效率分析结论：

（1）纯效率值普遍比全效率值高，进一步说明港口腹地进出口贸易总额对港口效率起正强化作用，在影响集装箱港口的众多外部因素中，港口腹地经济发展水平对港口产出和效率作用重大。从大型港口（深圳港、广州港）与小型港口（虎门港、中山港、珠海港）的比较可以看出，大型港口的效率值比小型港口的效率值表现稳定，说明大型港口更能抵抗腹地进出口贸易市场变动的影响，因为自2008年全球金融危机以来全球贸易和航运业持续低迷。

（2）理论上，在总资产不变的情况下，高的进出口贸易额导致高的产出和效率。但是2007年至2012年间，大的港口投资陆续完成、投入使用（如深圳大铲湾港区、广州南沙港二期、珠海高栏港二期、中山小榄港区等），港口效率在投资完成的当年出现大的下降。因为在集装箱运量没有明显增长的情况下，大的港口投资导致港口效率降低。

（3）就基础设施和机械设备而言，结合珠三角港口的实际情况和前述分析，水深和码头机械设备对港口效率和产出至关重要。水深条件是发展枢纽型集装箱港口的先决条件（如深圳港），这也是虎门港发展后续乏力的原因所在。港口机械数（本文中主要指桥吊数量和龙门吊数量）决定了港口的作业能力，港口机械的科学管理和机械资源的合理配置是提高集装箱港口产出和效率的关键因素。

（4）职工人数的多少对产出的影响微弱，在不影响正常运行的条件下，降低职工人数不影响产出。从这一点也可以得出结论：选用港口生产指标作为投入指标，研究集装箱港口效率优于选用港口财务指标，港口生产指标（基础设施、港口机械等）更能反映港口的复杂生产情况。

[1]Liu Z.The comparative Performance of Public and Private enterprises[J].Journal of Transportation Economies and Policy,1995,(9):263-274.

[2]Tongzon J L.Efficiency measurement of selected Australian and other international Ports using data envelopment analysis[J].Transportation Research,Part A,2001,35:113-128.

[3]罗俊浩,催蛾英,季建华.基于随机前沿分析（SFA）的港口上市公司的效率评价[J]. 武汉理工大学学报(交通科学与工程版),2012,8(4):736-739.

[4]黄勇,徐景昊.中国港口行业上市公司效率评价研究[J].水运工程,2010,(5):98-102.

[5]匡海波.中国港口效率测度研究[D].大连:大连理工大学,2007.

[6]张小蒂,邓娟.中国港口效率测度及提升研究[J].浙江大学学报(人文社会科学版),2013,43(4):29-31.

[7]刘大熔.多指标体系的港口效率评价模型[J].上海海运学院学报,1994,6(15):2-8.

[8]陈春芳,宗蓓华.基于SFA 法的上海港集装箱码头效率评价[J].上海海事大学学报,2008,9(29):87-92.

[9]Cullinane K P B,Song D W,Gray R.A Stochastic Frontier Model of the Efficiency of Major Container Terminals in Asia:Accessing the Influence of Administrative and Ownership Structures[J].Transportation Research,Part A,2002,36:743-762.