过氧烷基自由基分子内氢迁移反应类速率常数的计算

李尚俊 谈宁馨 姚 倩 李泽荣,* 李象远

(1四川大学化学学院,成都610064;2四川大学化学工程学院,成都610065)

1 引言

目前,由于燃料的使用越来越广泛,为了提高燃烧效应、减少排放,燃烧反应的研究越来越重要,大量的新实验和传统的实验技术应用于碳氢燃料的燃烧过程研究,与此同时,随着量子化学和反应速率理论的发展,在高温条件下碳氢燃料的燃烧模拟研究已经取得了很大成就,1,2发展建立了很多单组分碳氢燃料和不同混合燃料(如柴油、煤油)的替代燃烧模型,能较好地再现实验结果.但在低温条件下(T＜900 K),由于涉及反应类型较多,其中绝大多数反应类型缺乏反应速率系数的实验数据,因而在燃烧机理模型构建中,通常按反应类型规则给出近似速率系数,即同一反应类型中不同反应采用相同速率系数,或由基团加和方法给出近似速率系数,目前为止所建立的燃烧模型的模拟结果很多情形下不是太令人满意.3现在人们普遍认为,在碳氢燃料的高温燃烧和低温燃烧机理中,烷基自由基与氧气分子生成烷基过氧自由基(R+O2=ROO)的反应是最关键反应,该反应由于是强放热反应,其平衡常数强烈地依赖于温度,低温下有利于ROO的生成,而高温下有利于反应R+O2→R′+HO2的进行,因而该反应及后续反应在高温下不考虑,而在低温下起关键作用.4,5在其后续反应中,烷基过氧自由基ROO经分子内氢迁移形成氢过氧烷基自由基(QOOH)的反应为过氧烷基自由基的最主要消耗反应通道,6,7是低温燃烧反应中的一类重要基元反应,因而其精确的热力学和动力学参数是碳氢化合物低温燃烧模拟的基础.该类反应的过渡态为四元环、五元环、六元环等环状结构.Zádor等5给出了低温下碳氢化合物燃烧所涉及的关键基元反应类型,并报道了从C2到C5的烷基过氧自由基的分子内氢迁移反应的能垒计算的文献综述.

对该类反应中个别反应的计算研究,文献已有大量的报道.Miller等6在近G2水平计算得到了乙基过氧自由基(CH3CH2O2)的分子内氢迁移反应的能垒;Taatjes3对正丙基过氧自由基(CH3CH2CH2O2)分子内氢迁移反应进行了实验和量子化学计算研究,得到了近QCISD(T)水平的过渡态的能量,发现分子内氢迁移经六元环过渡态的能垒比经五元环过渡态的能垒更低.Villano等7,8在CBS-QB3水平计算得到了C1-C5的烷基过氧自由基的分子内氢迁移反应及逆反应的速率系数;Zhang等9在CBS-QB3水平计算得到了一些C3-C5烷基过氧自由基和烯基过氧自由基分子内氢迁移反应的能垒.由于在燃烧机理的构建与机理自动生成程序中,通常将反应按其相似性将其分为不同反应类,如对烷烃RH的夺氢反应根据夺氢基团分为:RH+O=R+OH反应类、RH+CHO=R+HCHO反应类、RH+H=R+H2反应类等等.且为方便起见,在机理自动生成程序中通常同一类分子反应的速率常数近似地采用同一数值.反应类的选取和划分,即所谓的反应规则,在燃烧机理的构建与机理自动生成程序中就很关键.但由于相似性没有严格的定义或标准,因而反应类的选取和划分往往是根据化学直觉或根据结果的好坏.对我们研究的烷基过氧自由基分子内氢迁移反应,人们发现不能简化为一类.Sharma等10按氢迁移距离及迁移氢所在碳原子类型,把烷基过氧自由基分子内氢迁移反应进一步划分为许多类型,在CBS-QB3水平计算得到了从(1,3)氢迁移到(1,8)氢迁移各反应类速率系数规则;Miyoshi11按氢迁移距离及迁移氢所在碳原子类型和过氧基所在碳原子类型,把该反应类进一步划分为许多子类型,在CBS-QB3水平计算得到了从(1,4)氢迁移到(1,8)氢迁移各反应类及逆反应各反应类速率系数规则.因此,为了精确描述烷基过氧自由基分子内氢迁移反应的反应规则,需要将其细分为很多类型.即便如此,研究发现在同一类中不同反应的速率常数相差较大,因而这种反应规则的方法对烷基过氧自由基分子内氢迁移反应有较大局限性.为了构建碳氢燃料可靠的低温燃烧机理,最可靠的办法是对烷基过氧自由基分子内氢迁移反应涉及的每一反应分别计算出精确的速率常数.但是,目前的量子化学高精度计算方法只能局限于较少碳原子数的烷基过氧自由基的分子体系.目前为止,文献报道的体系为C8及以下体系.本文的目的是通过将等键反应理论与过渡态理论相结合,计算得到C8以上烷基过氧自由基的分子体系分子内氢迁移反应的精确速率常数.

2 计算方法

单分子反应过渡态理论的反应速率常数表达式为:

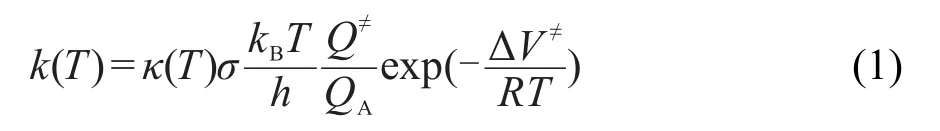
式中,κ为隧穿系数;R为理想气体常数;T为温度;σ是反应对称数;kB为Boltzmann常数;h为Planck常数;Q≠为过渡态配分函数;QA为反应物A的配分函数;ΔV≠为过渡态与反应物A的包含零点振动能的电子能之差,即反应能垒.在单分子反应过渡态理论速率常数的计算公式(1)中,振动贡献决定于过渡态和反应物的谐振频率,谐振频率的计算可在较低从头算级别计算.(1)式中关键项是势垒项,必须采用高精度计算方法才可得到精确数据.对于小分子的基元反应高精度的计算是可行的,但是,对于较大分子以及大分子的基元反应高精度的量子化学计算几乎是不可能的.

Truong等12-18以过渡态理论为基础,将反应类的概念引入反应类过渡态理论(RC-TST)中.该理论认为同一类反应中所有反应的活性中心相同,因此,任意两个反应的速率常数的不同主要在于取代基的不同.他们通常将同一类反应中最小反应体系定义为参考反应,其余反应成为目标反应.Truong等研究发现,参考反应与目标反应的能垒差随不同从头算理论方法变化而变化.但是,Truong等提出的反应类过渡态理论对反应类并没有给出严格定义,不能简单地用于烷基过氧自由基体系分子内氢迁移反应体系.

在我们的前期研究中,我们将等键反应方法引入了反应类的过渡态生成过程,19,20对反应类过渡态理论提供了解释,将等键反应的定义推广到非典型化学键的过渡态情形,并用于反应类目标反应能垒及速率常数的精确计算.

目标反应能垒表示如下:

式中,P代表参考反应,T代表目标反应,≠代表过渡态,Δʹ和 Δ分别为用高级别从头算方法精确计算和低级别从头算方法近似计算的参考反应的反应能垒,其差值ΔΔ为参考反应的能垒修正值.Δ为低级别从头算方法近似计算的目标反应的反应能垒,而Δʹ为对目标反应的反应能垒精确计算的估计.(2)、(3)式表明:目标反应的精确反应势垒可以由其低水平计算的近似结果通过参考反应的能垒修正值修正得到.同时,目标反应的速率常数kT可由低水平下的目标反应的速率常数kP及参考反应的能垒修正值得到:

本文选取了62个过氧烷基分子内氢迁移形成氢过氧化烷基自由基反应作为研究对象,反应见表S1(见Supporting Information).所有的量子化学计算都是在Gaussian 03程序21下进行.所有反应涉及到的物种的几何结构优化、频率计算和低级别单点计算均在B3LYP/6-311+G(d,p)22水平下进行,并用内禀反应坐标(IRC)理论对体系中所有反应过渡态与对应反应物和产物的关联性进行了确认.本文中所有振动均采用谐振子模型,没有考虑非谐效应对热力学参数及动力学参数的影响.热力学配分函数频率校正因子为0.9663,23高级别从头算方法采用模型化学方法CBS-QB3.24之所以选择CBS-QB3方法作为高精度的单点能计算,是因为Bozzelli等25用此方法计算了一系列过氧烷基分子的热力学参数,得到了与实验接近的结果.

3 结果与讨论

3.1 过渡态几何中心结构

过氧烷基分子内氢迁移反应的过渡态涉及碳上氢原子迁移到过氧自由基一端氧原子形成的环状结构,(1,3)氢迁移为四元环,(1,4)氢迁移为五元环,(1,5)氢迁移为六元环,(1,6)氢迁移为七元环,等等.该类反应中心所涉及到的原子,键长与键角编号如图 1所示,其中d1、d2、d3、d4为键长,A1、A2、A3为键角.

B3LYP/6-311+G(d,p)方法优化得到的各具体反应的反应中心过渡态几何结构参数列于表S2(见Supporting Information).由表S2可以看出,环状大小相同的过渡态结构几乎相同,所以本文对环状大小相同的过渡态反应中心的结构参数进行平均,其值列于表1.

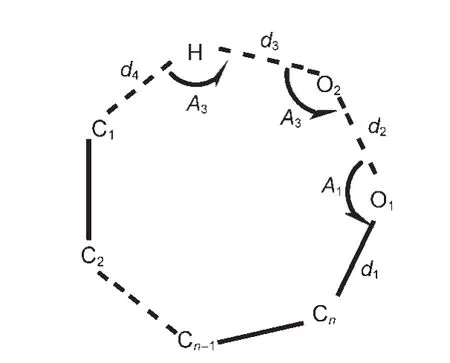
图1 过渡态(TS)反应中心的几何结构Fig.1 Geometry of the reaction centers in the transition states(TS)

从表1可以看出,按照氢迁移距离,从(1,3)氢迁移到(1,4)氢迁移、(1,5)氢迁移、(1,6)氢迁移,其反应中心过渡态几何结构参数变化明显,但从(1,6)氢迁移到(1,7)氢迁移、(1,8)氢迁移其几何结构参数很接近.因此,本文根据过氧烷基分子内氢迁移反应的反应中心过渡态几何结构参数是否守恒的特征,将(1,3)氢迁移、(1,4)氢迁移和(1,5)氢迁移各分为一类,而将(1,6)氢迁移、(1,7)氢迁移、(1,8)归为一类反应,即为((1,n),n=6,7,8).

为了更进一步反映这样划分的每一类反应过渡态几何结构是否守恒,表2给出了其几何结构参数的最大偏差和平均偏差.从表2可以看出,各类反应过渡态几何结构参数偏差很小,表明每一类反应其过渡态几何结构是守恒的,因此对这样划分的每一类反应,可以使用等键反应方法.本文将研究的62个反应分为(1,3),(1,4),(1,5),((1,n),n=6,7,8)四类反应,分别选取每一类反应的最简单反应,即表S1中R1、R11、R23、R57反应,作为参考反应,剩余58个反应为目标反应.

3.2 反应势垒

由于缺乏过氧烷基分子内氢迁移反应动力学参数实验报道,本文选用CBS-QB3方法作为参考反应的精确计算方法.同时在6-311+G(d,p)水平下,采用B3LYP方法作为参考反应的近似计算方法.两种方法计算得到的参考反应的反应势垒和反应焓变以及两种方法的差值结果列于表3.

从表3可以看出,低级别的B3LYP计算得到的参考反应势垒与高级别的CBS-QB3结果比较,有较大偏差,其偏差范围在2.70-11.06 kJ∙mol-1.所以,低级别的B3LYP计算得到的结果有较大误差,有必要对其修正.所以,本文对其余58个参考反应采用等键反应方法进行了修正,修正前后的反应势垒见表S3.对较小分子体系的部分目标反应,本文用高精度CBS-QB3方法进行了精确计算,其结果与用等键反应修正后反应势垒的比较列于表4.从表4可以看出,直接用密度泛函理论(DFT)方法计算的反应势垒的误差范围为-16.94--27.15 kJ∙mol-1,远超化学精度,但经等键反应方法修正以后,其误差范围变为-1.96-2.80 kJ∙mol-1,已在化学精度以内.因而,计算结果表明,过氧烷基分子内氢迁移反应用DFT方法经过等键反应方法修正可得到可靠的反应势垒.而且,从表S3可以看出,各迁移反应类型势垒与过渡态环状大小有关,呈现规律性变化,其变化规律为:(1,3)＞(1,4)＞(1,5)＞(1,6)＜(1,7)＜(1,8).

3.3 反应速率常数

本文根据过渡态理论及等键反应修正后势垒,19,20使用chemrate程序26对所涉及的62个反应计算了300-1500 K范围的速率参数,并按阿仑尼乌斯方程(见式(5)),经最小二乘法拟合得到动力学参数(A,Ea),结果列于表5中.

表1 反应中心过渡态平均几何结构参数Table 1 Average geometrical parameters of the reaction centers for the transition states

表2 每一类反应过渡态中心几何结构参数的最大绝对偏差(MAD)和平均绝对偏差(AAD)Table 2 Maximum absolute deviation(MAD)and average absolute deviation(AAD)of the geometrical parameters of the transition states for each class reaction

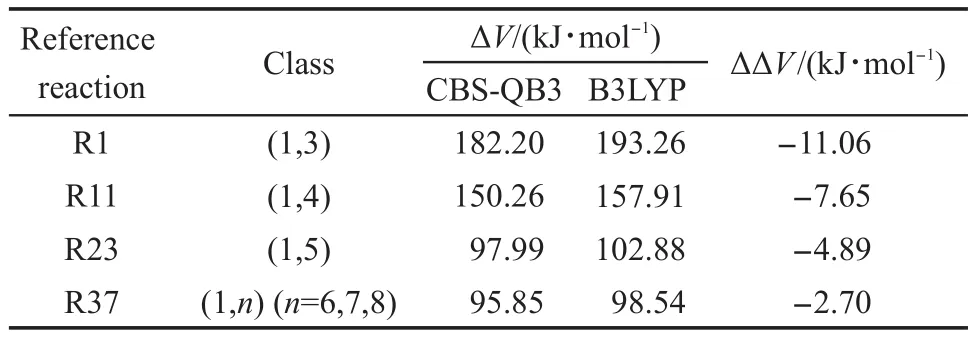
表3 参考反应的反应势垒Table 3 Energy barriers for the reference reactions

表4 B3LYP方法修正前后势垒与CBS-QB3结果比较Table 4 Comparison of B3LYPreaction barriers(Δ)before and after validation with the CBS-QB3 results

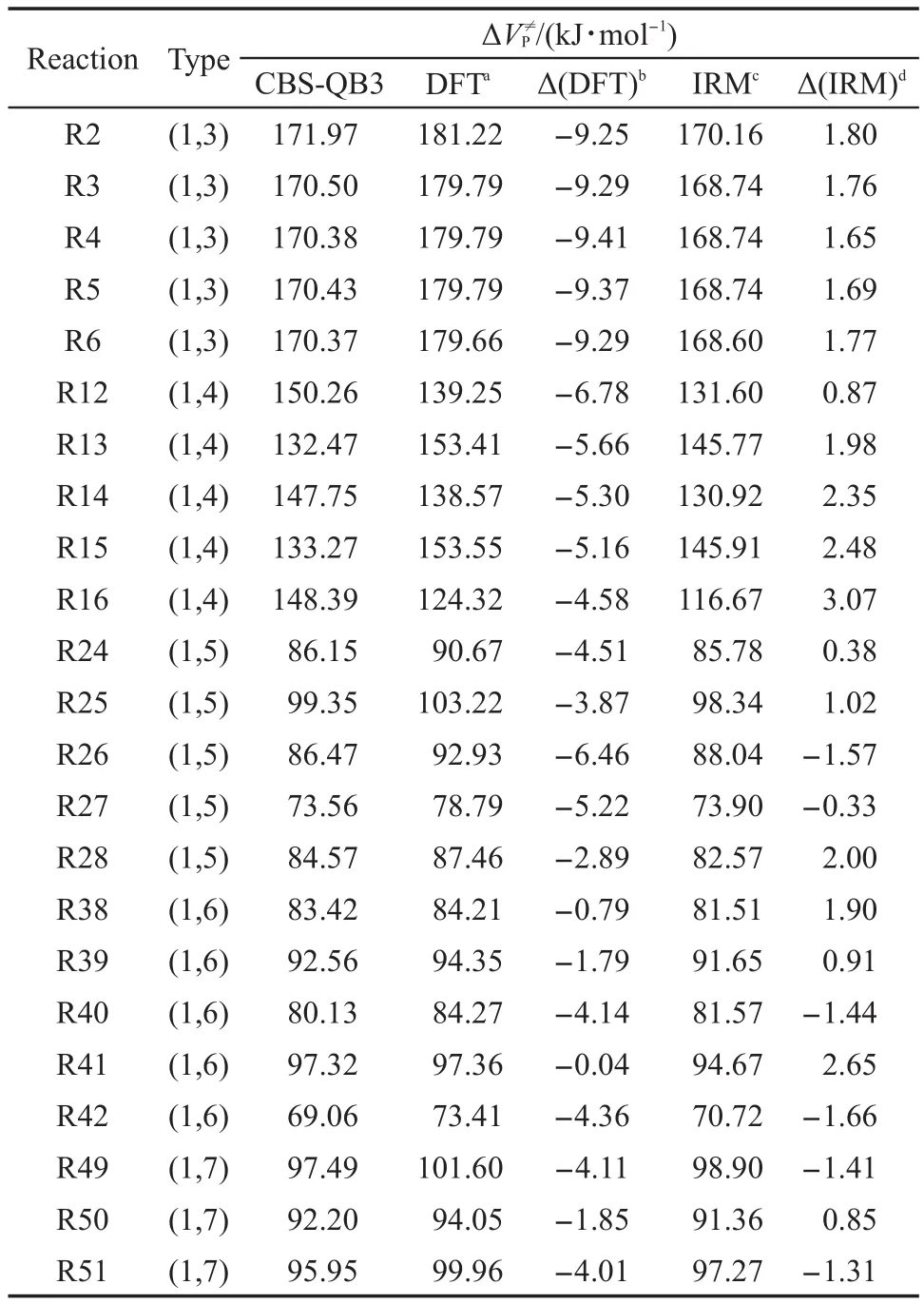
表4 B3LYP方法修正前后势垒与CBS-QB3结果比较Table 4 Comparison of B3LYPreaction barriers(Δ)before and after validation with the CBS-QB3 results

acalculated at the B3LYP/6-311+G(d,p)level of theory,bdifference between density functional theory(DFT)barrier and CBS-QB3 barrier:Δ(DFT)=ΔV(B3LYP)-ΔV(CBS-QB3),cDFT results after validation by isodesmic reaction method(IRM),ddeviation between IRM value and CBS-QB3 value:Δ(IRM)=ΔV(IRM)-ΔV(CBS-QB3)

Δ(IRM)d 1.80 1.76 1.65 1.69 1.77 0.87 1.98 2.35 2.48 3.07 0.38 1.02-1.57-0.33 2.00 1.90 0.91-1.44 2.65-1.66-1.41 0.85-1.31 Reaction R2 R3 R4 R5 R6 R12 R13 R14 R15 R16 R24 R25 R26 R27 R28 R38 R39 R40 R41 R42 R49 R50 R51 Type(1,3)(1,3)(1,3)(1,3)(1,3)(1,4)(1,4)(1,4)(1,4)(1,4)(1,5)(1,5)(1,5)(1,5)(1,5)(1,6)(1,6)(1,6)(1,6)(1,6)(1,7)(1,7)(1,7)ΔVP≠/(kJ∙mol-1)CBS-QB3 171.97 170.50 170.38 170.43 170.37 150.26 132.47 147.75 133.27 148.39 86.15 99.35 86.47 73.56 84.57 83.42 92.56 80.13 97.32 69.06 97.49 92.20 95.95 DFTa 181.22 179.79 179.79 179.79 179.66 139.25 153.41 138.57 153.55 124.32 90.67 103.22 92.93 78.79 87.46 84.21 94.35 84.27 97.36 73.41 101.60 94.05 99.96 Δ(DFT)b-9.25-9.29-9.41-9.37-9.29-6.78-5.66-5.30-5.16-4.58-4.51-3.87-6.46-5.22-2.89-0.79-1.79-4.14-0.04-4.36-4.11-1.85-4.01 IRMc 170.16 168.74 168.74 168.74 168.60 131.60 145.77 130.92 145.91 116.67 85.78 98.34 88.04 73.90 82.57 81.51 91.65 81.57 94.67 70.72 98.90 91.36 97.27

图2中给出了在300-1000 K温度范围内本文计算的部分反应速率常数与文献实验值和其他计算值的比较示意图.对(1,4)小分子氢迁移反应(R11):CH3CH2OO∙➝∙CH2CH2OOH(见图2A),Sharma等10用CBS-QB3高精度水平下计算得到500 K时速率常数为5.48×10-4s-1,而Sheng等27用CBS-Q//B3LYP/6-31G(d,p)方法所得值为1.18×10-4s-1,Huynh等28用CBS-QB3方法计算所得500 K时速率常数为2.78×10-4s-1,Baldwin等29得到的实验值为5.04×10-3s-1,本文通过等键反应计算得到该温度下常数为1.26×10-3s-1,与实验值非常接近.对(1,4)氢迁移反应类型中(R16):(CH3)2CHCH2OO∙➝(CH3)C∙CH2OOH(见图2B),Sharma等10用CBS-QB3方法计算得500 K时速率常数为4.75×10-1s-1,Baldwin等29实验值2.46×101s-1,而本文通过等键反应计算出速率常数为2.31 s-1,与实验值接近.同时,本文用等键反应方法计算得到的反应R24、R38、R49的速率常数也与实验值符合较好,因而本文为过氧烷基分子内氢迁移这一类型反应提供了可靠和准确的动力学数据.

表5 反应动力学参数(A,Ea)Table 5 Reaction kinetic parameters(A,Ea)

图2 本文计算的速率常数与文献值比较Fig.2 Comparison of rate constants calculated in this study with those reported in other studies

4 结论

在B3LYP/6-311+G(d,p)方法下优化得到了过氧烷基分子内氢迁移反应的过渡态,提出了根据过渡态反应中心几何结构是否守恒作为反应类的判据,并将过氧烷基分子内氢迁移反应划分为(1,3),(1,4),(1,5),((1,n),n=6,7,8)四种反应类型.将过渡态理论与反应类等键反应方法结合,对B3LYP/6-311+G(d,p)方法水平计算得到的过氧烷基氢迁移反应体系中62个反应的势垒、焓变和速率常数进行了修正,所得结果与高精度CBS-QB3方法计算结果和实验结果一致.因此,本文通过反应类等键反应方法解决了反应类的严格定义和大分子体系的过氧烷基分子内氢迁移反应的动力学参数的精确计算问题,对碳氢化合物的低温燃烧机理研究具有重要意义.

Supporting lnformation:Table S1 listed all reactions.Optimized geometrical parameters of the reaction centers of the transition states were given in Table S2.Table S3 listed all reaction barriers,reaction enthalpy changes.This information is available free of chargeviathe internet at http://www.whxb.pku.edu.cn.

(1) Battin-Leclerc,F.Prog.Energy Combust.Sci.2008,34,440.doi:10.1016/j.pecs.2007.10.002

(2) Pousse,E.;Glaude,P.A.;Fournet,R.;Battin-Leclerc,F.Combust.Flame2009,156,954.doi:10.1016/j.combustflame.2008.09.012

(3) Taatjes,C.A.J.Phys.Chem.A2006,110,4299.doi:10.1021/jp056997f

(4) Walker,R.W.;Morley,C.Basic Chemistry of Combustion.InLow-Temperature Combustion and Autoignition;Pilling,M.J.Ed.;Elsevier:Amsterdam,The Netherlands,1997;pp 1-124.

(5) Zádor,J.;Taatjes,C.A.;Fernandes,R.X.Prog.Energy Combust.Sci.2011,37,371.doi:10.1016/j.pecs.2010.06.006

(6) Miller,J.A.;Klippenstein,S.J.;Robertson,H.Proc.Combust.Inst.2000,28,1479.doi:10.1016/S0082-0784(00)80544-5

(7)Villano,S.M.;Huynh,L.K.;Carstensen,H.H.;Dean,A.M.J.Phys.Chem.A2012,116,5068.doi:10.1021/jp3023887

(8)Villano,S.M.;Huynh,L.K.;Carstensen,H.H.;Dean,A.M.J.Phys.Chem.A2011,115,13425.doi:10.1021/jp2079204

(9) Zhang,F.;Dibble,T.S.J.Phys.Chem.A2011,115,655.doi:10.1021/jp1111839

(10)Sharma,S.;Raman,S.;Green,W.H.J.Phys.Chem.A2010,114,5689.doi:10.1021/jp9098792

(11) Miyoshi,A.J.Phys.Chem.A2011,115,3301.doi:10.1021/jp112152n

(12) Truong,T.N.J.Chem.Phys.2000,113,4957.doi:10.1063/1.1287839

(13)Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J.Phys.Chem.A2006,110,473.doi:10.1021/jp051280d

(14)Muszynska,M.;Ratkiewicz,A.;Huynh,L.K.;Truong,T.N.J.Phys.Chem.A2009,113,8327.doi:10.1021/jp903762x

(15) Bankiewicz,B;Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J.Phys.Chem.A2009,113,1564.doi:10.1021/jp808874j

(16) Zhang,S.W.;Truong,T.N.J.Phys.Chem.A2003,107,1138.doi:10.1021/jp021265y

(17)Kungwan,N.;Truong,T.N.J.Phys.Chem.A2005,109,7742.doi:10.1021/jp051799+

(18) Huynh,L.K.;Truong,T.N.Theor.Chem.Account2008,120,107.doi:10.1007/s00214-007-0311-9

(19)Wang,B.Y.;Li,Z.R.;Tan,N.X.;Yao,Q.;Li,X.Y.J.Phys.Chem.A2013,117,3279.doi:10.1021/jp400924w

(20)Wang,B.Y.;Tan,L.X.;Yao,Q.;Li,Z.R.;Li,X.Y.Acta Phys.-Chim.Sin.2012,28,2824.[汪必耀,谈宁馨,姚 倩,李泽荣,李象远.物理化学学报,2012,28,2824.]doi:10.3866/PKU.WHXB201209053

(21) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03,Revision B.01;Gaussian Inc.:Pittsburgh,PA,2003.

(22) Scott,A.P.;Radom,L.J.Phys.Chem.1996,100,16502.doi:10.1021/jp960976r

(23)NIST.Computational Chemistry Comparison and Benchmark Database.NIST Standard Reference Database Number 101.2013,available at http://webbook.nist.gov/

(24) Montgomery,J.A.;Frisch,M.J.;Ochterski,J.W.;Petersson,G.A.J.Chem.Phys.1999,110,2822.doi:10.1063/1.477924

(25) Zhu,L.;Bozzelli,J.W.;Kardos,L.M.J.Phys.Chem.A2007,111,6361.doi:10.1021/jp070342s

(26) Mokrushin,V.;Tsang,W.Chemratev.1.5.8;National Institute of Standards and Technology:Gaithersburg,MD,2009.

(27)Sheng,C.Y.;Bozzelli,J.W.;Dean,A.M.;Chang,A.Y.J.Phys.Chem.A2002,106,7276.doi:10.1021/jp014540+

(28)Huynh,L.K.;Carstensen,H.H.;Dean,A.M.J.Phys.Chem.A2010,114,6594.

(29)Baldwin,R.R.;Hisham,M.W.M.;Walker,R.W.J.Chem.Soc.Faraday Trans.11982,78,1615.doi:10.1039/f19827801615