基于直接横摆力矩的四轮转向/驱动滑模控制*

赵立军　邓宁宁　罗念宁　刘昕晖

(1.哈尔滨工业大学(威海)汽车工程学院, 山东 威海 264209； 2.吉林大学 机械科学与工程学院, 吉林 长春 130025)

基于直接横摆力矩的四轮转向/驱动滑模控制*

赵立军1,2邓宁宁1罗念宁1刘昕晖2

(1.哈尔滨工业大学(威海)汽车工程学院, 山东 威海 264209； 2.吉林大学 机械科学与工程学院, 吉林 长春 130025)

摘要：针对四轮独立转向/驱动车辆的转向稳定性问题，提出一种基于直接横摆力矩的滑模变结构控制算法.根据Ackerman转向模型计算车辆前后轮转向角之间的关系,并根据零质心侧偏角控制目标计算车辆各轮的转向角;设计以横摆角速度和质心侧偏角为控制目标的滑模变结构控制算法,对各轮转向角和驱动力矩进行控制.运用Lyapunov方法证明了该算法的稳定性,最后利用Matlab/Simulink仿真软件对控制算法进行仿真分析.结果表明，该控制算法可以将质心侧偏角和横摆角速度控制在理想范围内,从而有效提高车辆转向稳定性.

关键词：四轮转向;四轮驱动；转向稳定性;直接横摆力矩;滑模变结构

四轮独立转向/驱动车辆能够进行各轮的独立转向和驱动/制动控制,可使车辆在低速行驶时通过前后轮反向偏转来减小转向半径，高速行驶时通过前后轮同向偏转来提高操纵稳定性.虽然四轮独立转向/驱动车辆造价高、结构复杂,但对某些特种车辆而言具有重要意义[1].四轮独立转向/驱动车辆采用液压或电动轮边驱动机构以及电液控制转向机构[2],并通过专门的结构设计来实现车辆的四轮独立转向和驱动.

四轮独立转向/驱动车辆的转向稳定性非常重要.提高车辆转向稳定性的方法有很多：Shino等[3-4]采用直接横摆力矩控制方法分别设计了基于状态反馈控制和模糊控制的稳定性控制策略;Naoki等[5]研究了基于最小二乘法原理的纵横向动力学分配方法来对车辆的稳定性进行控制;Tahami等[6]研究了四轮驱动电动汽车辅助系统,其以横摆角速度为控制对象,采用模糊理论对车辆的稳定性进行控制;胡爱军等[7-8]均将横摆力矩和主动前轮转向结合起来,分别运用H2/H∞集成控制和LPV/H∞控制来进行车辆的稳定性控制.不过目前的研究大都集中于前轮转向车辆的转向稳定性,对于四轮独立转向/驱动车辆的转向稳定性研究则未见报道.直接横摆力矩控制是通过对车辆每个车轮进行独立的驱动/制动控制,从而产生横摆力矩来克服车辆的过多转向或不足转向,从而提高其转向稳定性.这种控制方法可以使轮胎的纵向力不受来自车辆侧向运动的影响.由于文中车辆具有可以进行各轮独立驱动/制动的特点,故采用基于直接横摆力矩的滑模变结构控制算法,对四轮转向/驱动车辆的转向/驱动控制进行研究.

1车辆前后轮转角关系

车辆Ackermann转向模型[9]如图1所示.

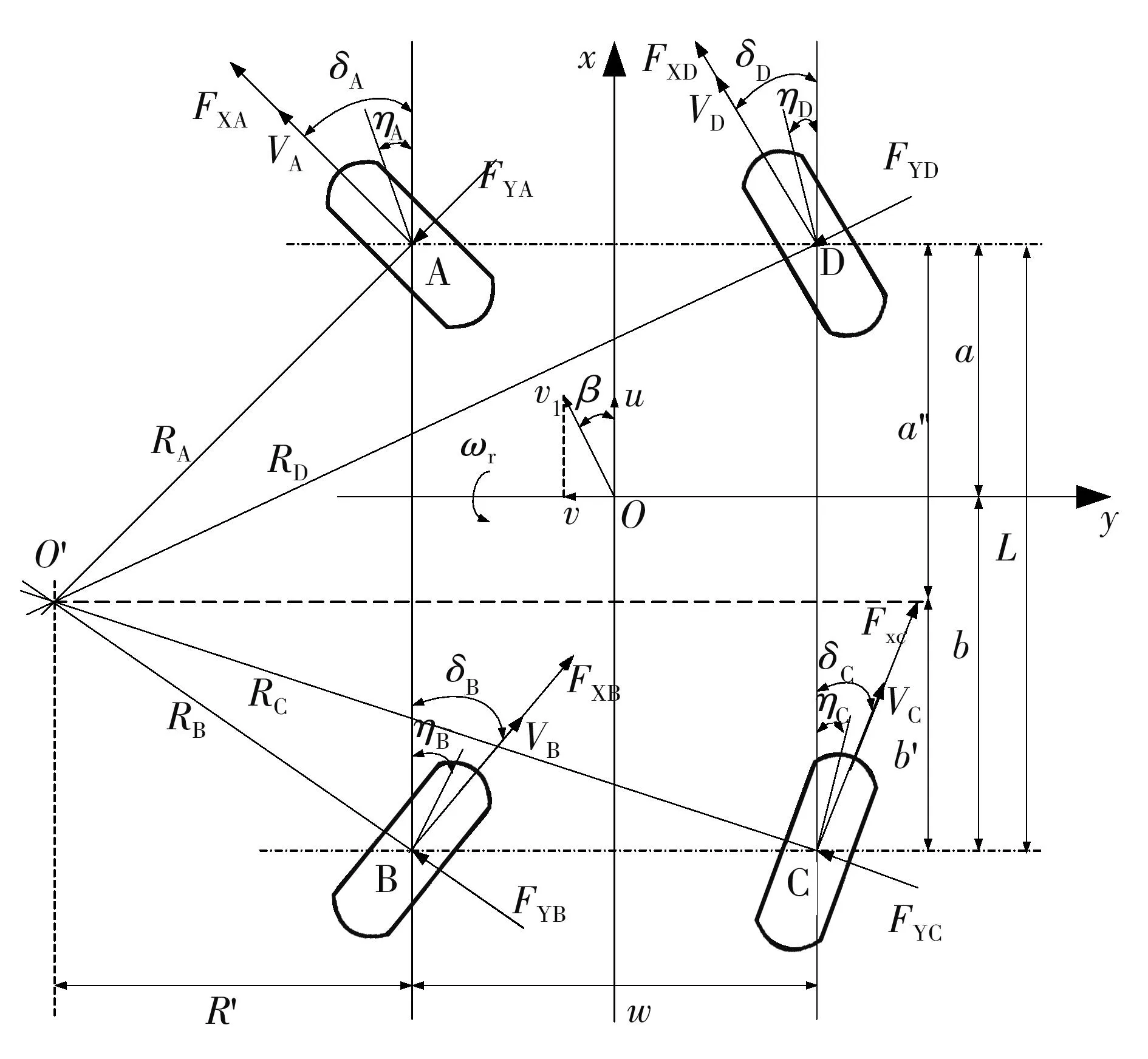
图1　Ackermann转向原理Fig.1　Ackermann steering principle

根据图1可以得到两后轮转角与两前轮转角之间的关系为

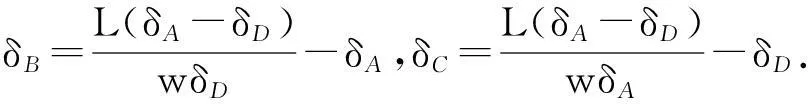
式中：δi(i代表A,B,C,D)为车轮转向角度,rad;L为轴距,m;w为左右轮间距,m.

车辆各个轮胎的侧偏角为

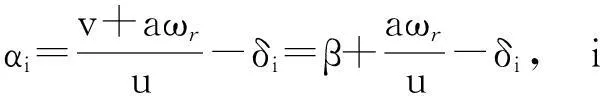
式中：αi、αj为轮胎侧偏角,rad;v、u分别为车辆侧向、纵向速度,m/s;a、b分别为车辆前轮、后轮到车辆质心的距离,m;ωr为车辆横摆角速度,rad/s;β为车辆质心侧偏角,rad.

2车辆控制模型的建立

由图1得到车辆线性二自由度模型的动力学方程如下:

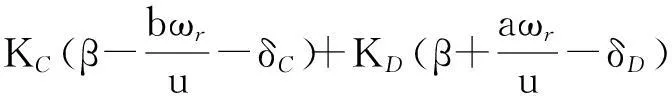
(1)

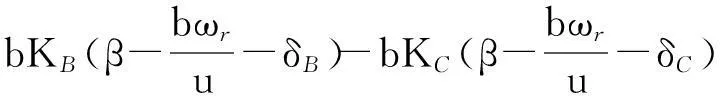
(2)

式中：m为整车质量,kg;Ki(i代表A,B,C,D)为轮胎侧偏刚度,N/rad;Iz为整车质量绕z轴的转动惯量,kg·m2.

车辆转向稳定性的重要参考指标是质心侧偏角[10].对于前轮转向车辆而言,其质心侧偏角只有在某一特定车速下才接近于0,这会降低车辆的转向稳定性极限.而四轮独立转向车辆能够保证车辆的质心侧偏角在比较宽的行驶速度范围内都接近0[11].

(3)

式中,m1=(2LaKfKr-mu2bKr)L.

由此可以得到各轮转角之间的关系为

(4)

式中，k1-k4均为比例系数.

文中通过直接横摆力矩控制来保证其转向稳定性,因此将式(1)、(2)改写如下:

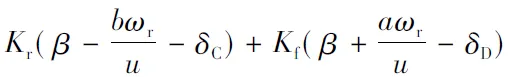
(5)

(6)

式中,T为横摆力矩,N.

将式(5)、(6)表示为系统的状态空间表达式形式,即

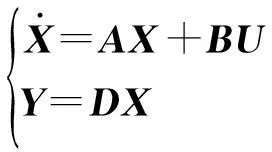
(7)

3滑模变结构控制

滑模变结构控制具有算法较为简单、响应时间短以及抗干扰能力强等优点,考虑车辆实际运行时的响应速度以及抗干扰需求,文中选用此算法对四轮转向/驱动车辆的各轮转向角和驱动/制动力矩进行控制[12].

3.1　车辆参考模型的建立

车辆的参考模型形式如下式所示[13]:

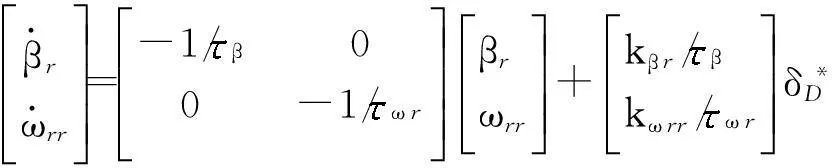
将其写为状态空间表达式的形式:

(8)

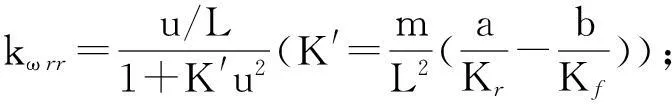
3.2　基于横摆力矩的滑模变结构控制

定义实际值与参考值之间的误差е为

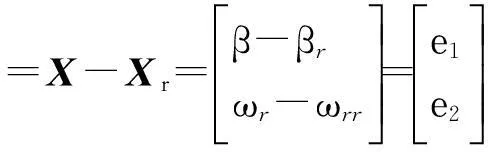
(9)

将式(7)、(8)代入到式(9)中,得

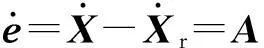
(10)

滑模变结构的切换函数定义为

(11)

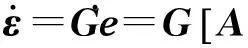
(12)

式中,g1、g2是该切换函数的待定参数,两参数的选取应注意使得矩阵G为满秩常数矩阵,G矩阵应使得矩阵GB为非奇异矩阵.

为了实现滑模变结构的滑动模态运动,采用等速趋近律设计[14],即令

(13)

式中,q1、q2是待定参数,其值为正.这样的设计能够使系统在Lyapunov函数下保证滑模运动,并且只要选取合适的q1、q2值就能够使得系统运动形态受控,在设计者期望的时间内到达设定的切换面.

联合式(12)、(13)可以得到控制输入量为

(GB)-1Qsgn(ε)

(14)

从式(14)中可以看出GB矩阵应是满秩矩阵.

将已知参数代入式(14),化简可得控制输入向量为

(15)

式中,λ1=KfK1+KrK2+KrK3+KfK4，

λ2=aKfK1-bKrK2-bKrK3+aKfK4，

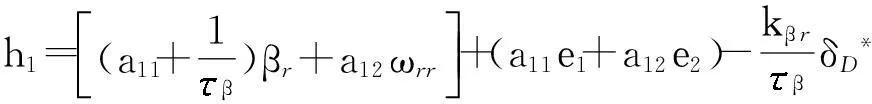
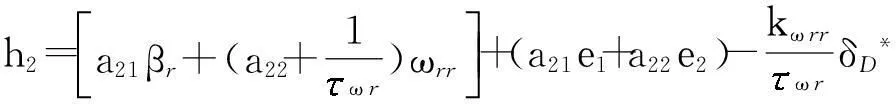
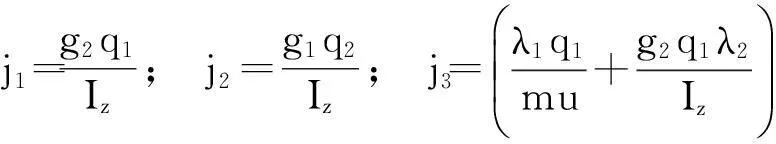
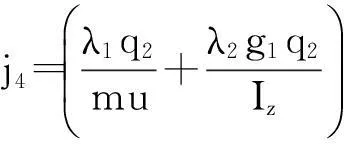
3.3　控制算法稳定性分析

构造Lyapunov函数如下:

V=εTWε.

由此得

(16)

将式(11)、(13)代入到式(16),化简计算得:

(17)

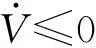
4滑模变结构控制仿真分析

在Matlab/Simulink中搭建仿真模型.模型主要包括汽车参考模型、汽车2自由度模型、滑模控制模型以及Ackermann转向模型等.仿真参数如表1所示.

表1　车辆仿真模型参数Table1　Parametersofvehiclesimulationmodel

4.1　低速行驶转向工况仿真分析

车辆进行低速转向行驶时,为了验证滑模变结构控制的有效性,取两组值进行验证.第1组值设车辆的速度为10.8 km/h,右前轮转向角初始值为0,斜率为0.2 rad/s,经过1s后达到0.2 rad,然后保持不变;第2组值设速度为15 km/h,右前轮转向角为0.3 rad.其仿真分析结果如图2、3所示.

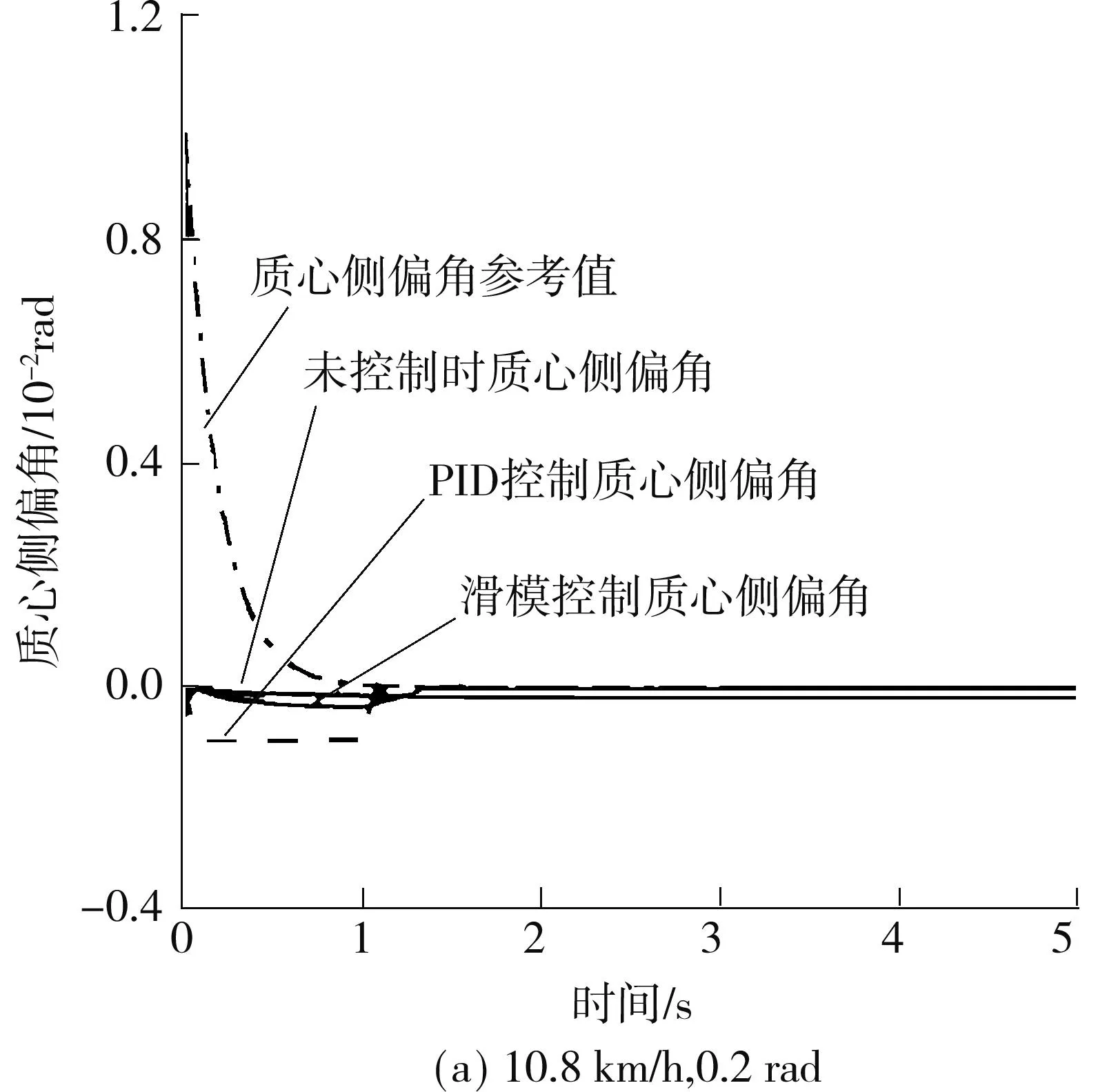
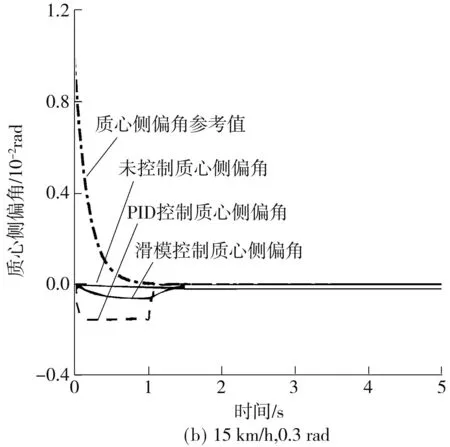
图2　低速行驶转向工况质心侧偏角Fig.2　Side slip angle at low speed and on steering

对比图2中(a)和2(b)可以看出,低速时,车辆的行驶速度与转角的变化对质心侧偏角影响不大,这是由于在控制车辆的各轮转角时已经保证了车辆的质心侧偏角为0.另外进行滑模控制之后的质心侧偏角较未控制前的侧偏角值距离零值远,这是由于采用控制后系统内部干扰引起的.不过从绝对值上来看，两者相差非常小,都非常接近零值,可以认为滑模控制很好地达到了预期目标.对比图3(a)和3(b)可以看出,随着车辆行驶速度与转向角度的增大,车辆的横摆角速度也在变大.另外可以看出进行控制之后的横摆角速度较未进行控制之前的值,明显地更接近参考值,得到了很好的控制效果.因此总体来看,进行滑模控制之后的车辆稳定性有了明显提高.比较滑模控制与PID控制,可以看出,两种控制方法的控制效果很接近,但是滑模控制在控制响应时间和绝对值方面都优于PID控制.

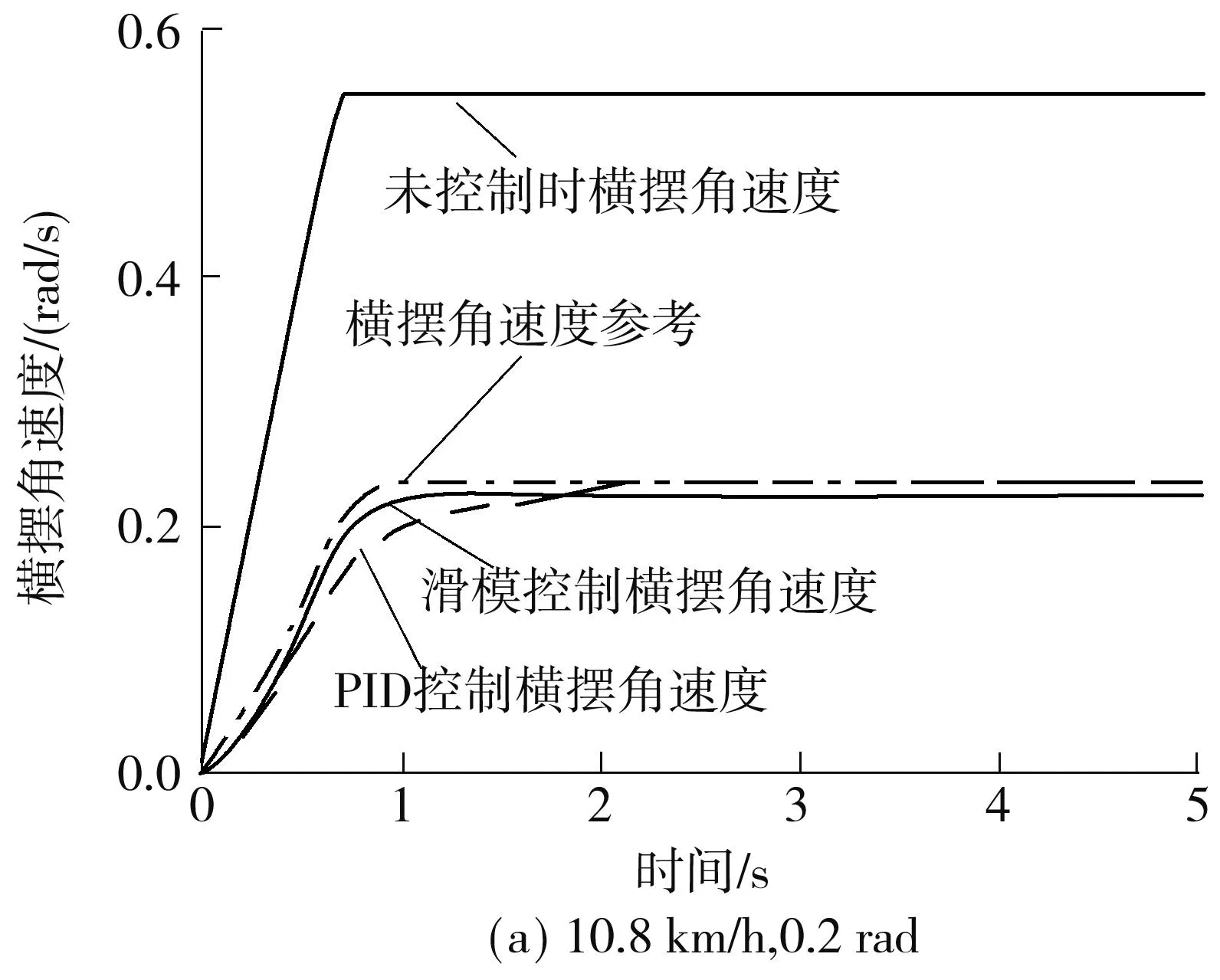
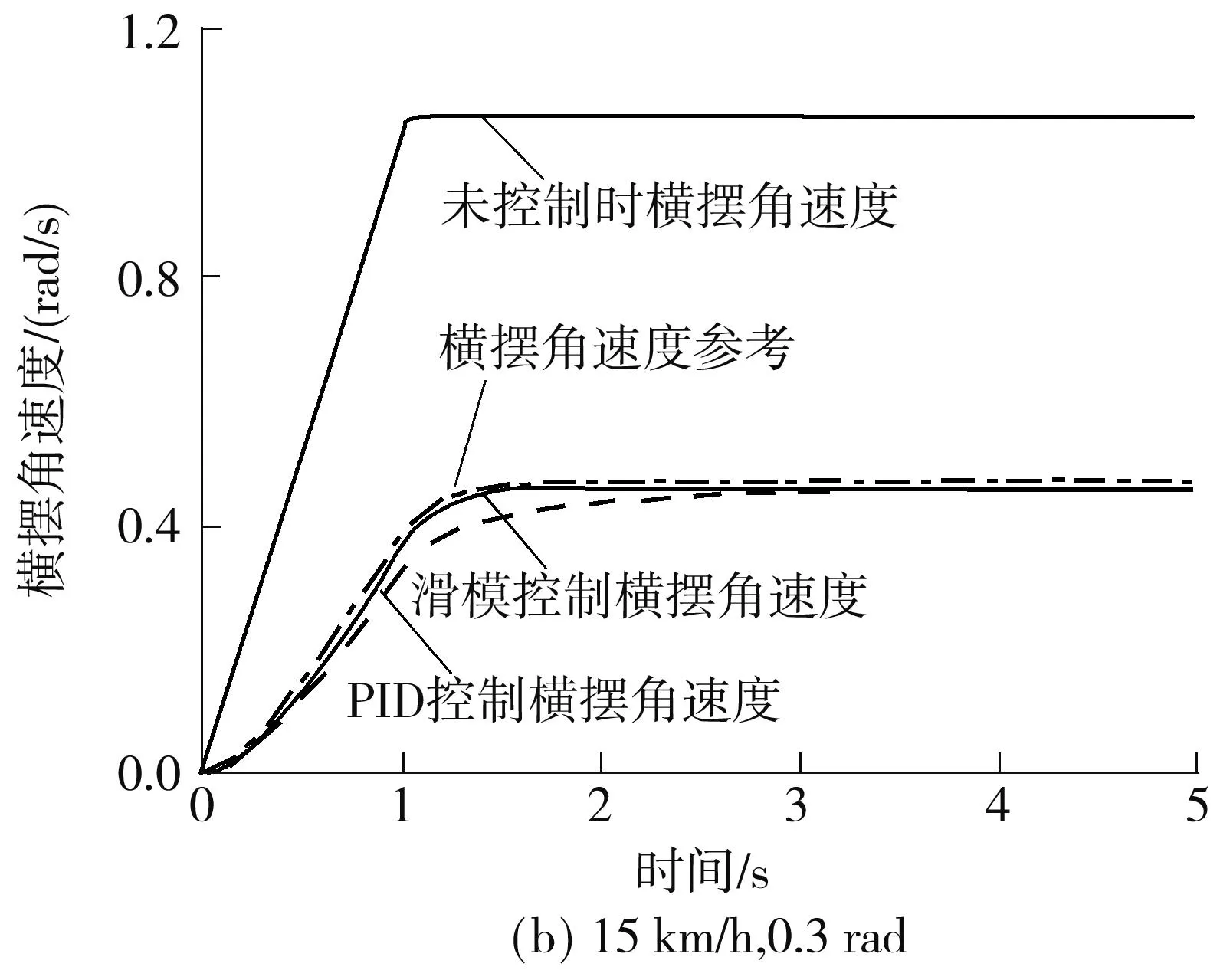
图3　低速行驶转向工况横摆角速度Fig.3　Yaw velocity at low speed and on steering

图4、5所示为车辆在第1组值的情况下转向时各轮转角以及转向半径.由图4可以看出,低速行驶时,四轮转向/驱动车辆两后轮的转角与两前轮的转角方向相反.这就使得在相同的速度与转向角输入情况下,能够进行四轮独立转向的车辆,其转向半径相较于传统的前轮转向车辆而言减小了近42%,如图5所示.对于某些地方相对狭窄而车辆必须进行转向的情况而言,这无疑具有很大的优势.

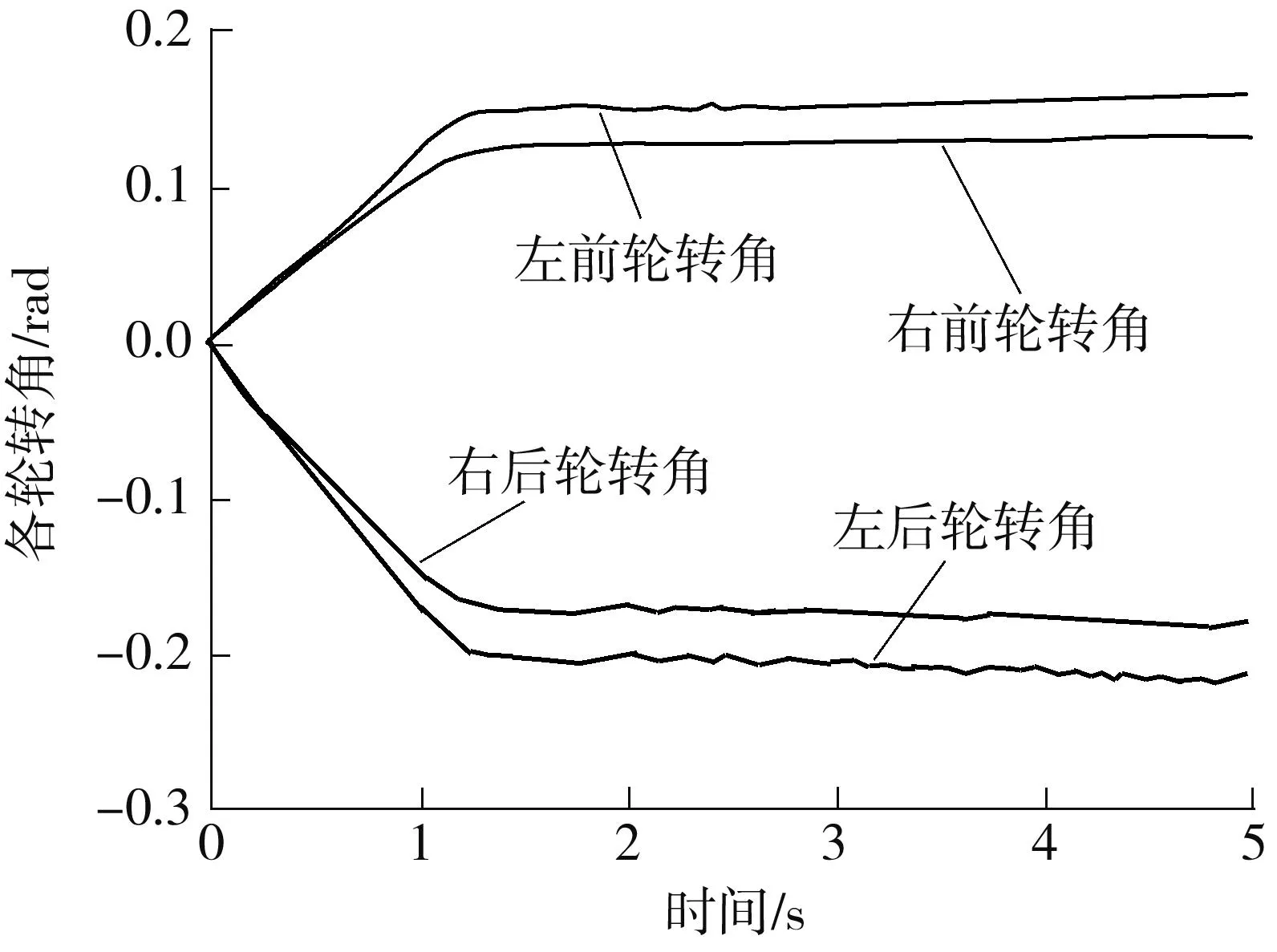
图4　低速行驶转向工况车辆各轮转角Fig.4　Angle of each wheel at low speed and on steering

图5　低速行驶转向工况车辆转向半径Fig.5　Vehicle steering radius at low speed and on steering

4.2　高速行驶转向工况仿真分析

车辆进行高速转向行驶时,为了验证滑模变结构控制的有效性,同样地取两组值进行验证.第1组值设车辆的速度为72 km/h,右前轮转向角初始值为0,斜率为0.05 rad/s,经过1s后达到0.05 rad,然后保持不变;第2组值设速度为80 km/h,右前轮转向角为0.03 rad. 仿真结果如图6-8所示.

与车辆低速行驶时情况类似,分别对比图6、图7(a)和7(b)可以看出,进行滑模控制之后的质心侧偏角和横摆角速度都非常接近参考值,很好地达到了预期目标,提高了车辆的稳定性.与PID控制相比,滑模控制在响应时间方面要更好一些.进行滑模控制之后,质心侧偏角值和横摆角速度值有很小幅波动,这是滑模控制的固有缺陷.在实际运用中可根据需求和系统特性采取减小波动的措施[15-16].图8为在第1组值下的各轮转角,可以看出,当车辆以较高速度行驶时,车辆的前后轮同向转动.

车辆实际运行时,车轮的垂直载荷发生变化会导致轮胎侧偏刚度产生波动,在本控制系统中按照干扰进行处理.

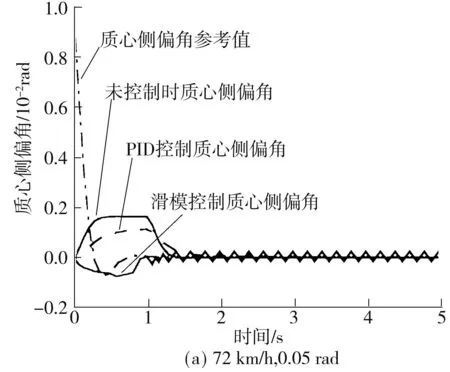
图6　高速行驶转向工况质心侧偏角Fig.6　Side slip angle at high speed and on steering

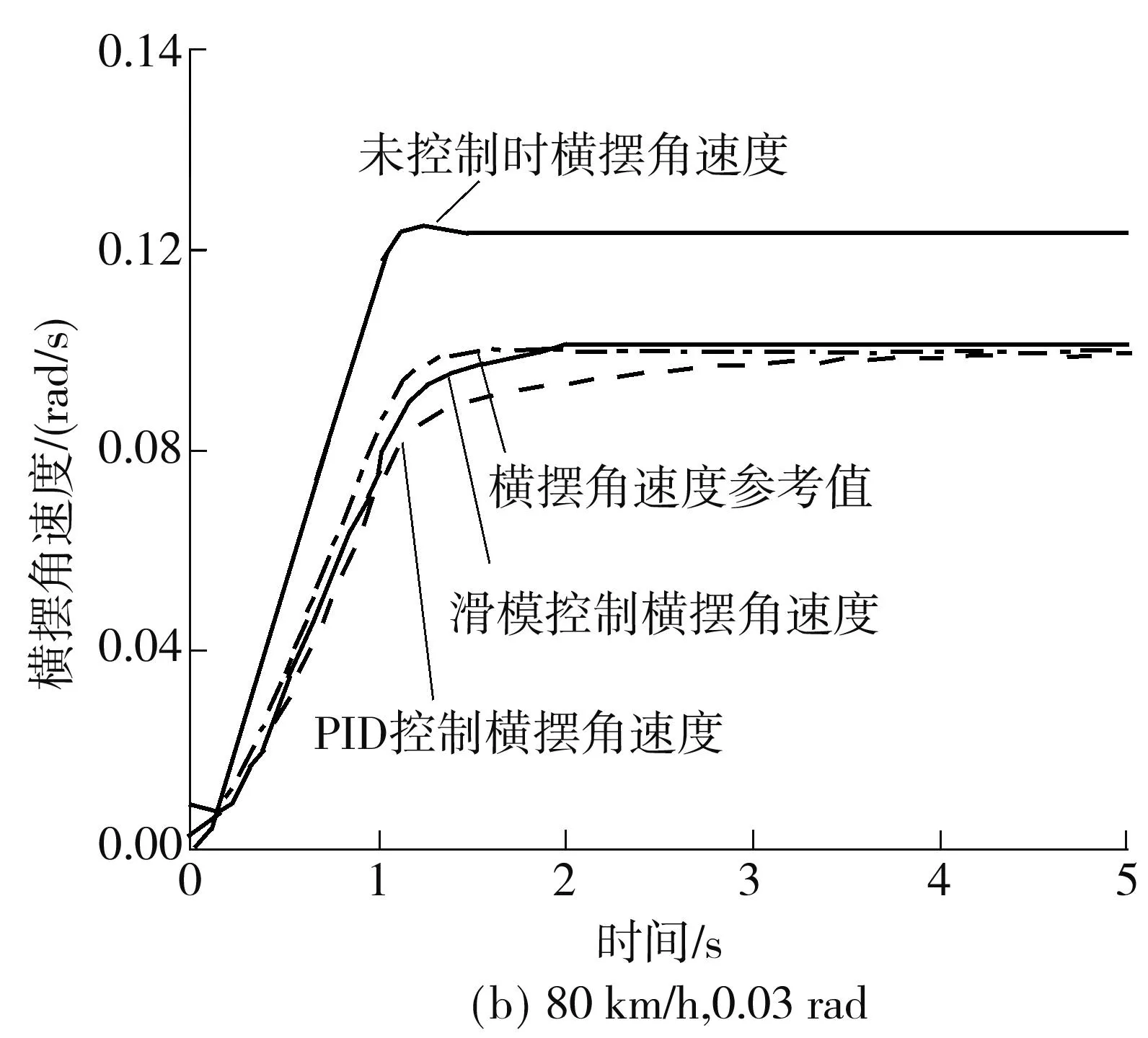
图7　高速行驶转向工况横摆角速度Fig.7　Yaw velocity at high speed and on steering

图8　高速行驶转向工况车辆各轮转角Fig.8　Angle of each wheel at high speed and on steering

5结语

针对四轮独立转向/驱动车辆,提出了基于直接横摆力矩的滑模变结构控制算法,通过控制车辆各轮转向角和横摆力矩来提高车辆转向稳定性.仿真分析表明,该控制算法可以使车辆行驶时的横摆角速度很好地跟踪理想横摆角速度,并且使得质心侧偏角基本保持为零.由此可充分发挥各轮独立转向/驱动车辆的优点：低速转向行驶时车辆前后轮反向偏转,转向稳定且转向半径小;高速转向行驶时车辆前后轮同向偏转,车辆操纵稳定性得以提高.

参考文献：

[1]孙文刚.飞机牵引车转向系统研究 [D].西安：长安大学工程机械学院，2008.

[2]刘彩志，陈思忠，陈茜.四轮独立转向汽车比例方向阀驱动电路设计 [J].机电工程，2002，19(5)：23-25.

Liu Cai-zhi,Chen Si-zhong,Chen Xi.The design of driver electrocircuit of proportion direction control valve of the four wheel steering [J].Mechanical and Electrical Engineering,2002,19(5)：23-25.

[3]Shino M,Nagai M.Independent wheel torque control of small scale electric vehicle for handling and stability improvement [J].JSAE Review,2003,24：449-456.

[4]Zhou L,Ou L L,Wang C.A simulation of the four-wheel steering vehicle stability based on DYC control [C]∥Measuring Technology and Mechatronics Automation.Zhangjiajie：MTMA,2009：189-193.

[5]Naoki A,Hiroshi F.Yaw-rate control for electric vehicle with active front/rear steering and driving/braking force distribution of rear wheels [C]∥Advanced Motion Control 2010.Nagaoka：AMC,2010：726-731.

[6]Tahami F,Kazemi R,Farhanghi S.A novel driver assist stability system for all wheel drive electric vehicle [J].IEEE Transactions on Vehicular Technology,2003,52(3):683-692.

[7]胡爱军，王朝晖.主动前轮转向与直接横摆力矩H2/H∞集成控制 [J].河南科技大学学报：自然科学版，2010，31(6)：24-28.

Hu Ai-jun,Wang Zhao-hui.Active front steering and direct yaw momentH2/H∞integrated control [J].Journal of Henan University of Science and Technology：Natural Science,2010,31(6)：24-28.

[8]Doumiati M,Sename O,Martinez J,et al.Gain-scheduled LPV/H∞controller based on direct yaw moment and active steering for vehicle handling improvements [C]∥49th IEEE Conference on Decision and Control.Atlanta：CDC,2010：6427-6432.

[9]Ackermann J,Odenthal D,Bunte T.Advantages of active steering for vehicle dynamics control [C]∥Automotive Technology and Automation,32nd International Symposium on Automotive.Vienna:[s.n.],1999.

[10]Avesta Goodarzi,Ebrahim Esmailzadeh.Design of a VDC system for all wheel independent drive vehicles [J].IEEE/ASME Transactions on Mechatronics,2007,12(6)：632-639.

[11]郭孔辉，轧浩.四轮转向的控制方法的发展 [J].中国机械工程，1998，9(5)：73-75.

Guo Kong-hui,Ya Hao.The development of four wheels steering control method [J].China Mechanical Engineering,1998,9(5)：73-75.

[12]王伟达，张为，丁能根，等.汽车DYC系统的二阶滑模控制 [J].华南理工大学学报：自然科学版，2011,39(1)：141-146.

Wang Wei-da,Zhang Wei,Ding Neng-gen,et al.Second-order sliding mode control of vehicular DYC system [J].Journal of South China University of Technology:Natural Science Edition,2011,39(1)：141-146.

[13]Will Anthony B,Zak Stanislaw H.Modelling and control of an automated vehicle [J].Vehicle System Dynamics,1997,27(3)：131-155.

[14]胡跃明.变结构控制理论与应用 [M].北京：科学出版社，2003.

[15]Meliksah Ertugrual,Okyay Kaynak.Neuro sliding mode control of robotic manipulators [J].Mechatronics,2000,10(1/2)：239-263.

[16]Wong L J,Leung F H F,Tam P K S.A chattering elimination algorithm for sliding mode control of uncertain non-linear systems [J].Mechatronics,1998,8(7)：765-775.

Four-Wheel-Steering/Driving Sliding Mode Control Based on Direct Yaw Moment

ZhaoLi-jun1,2DengNing-ning1LuoNian-ning1LiuXin-hui2

(1．School of Automobile Engineering,Harbin Institute of Technology at Weihai,Weihai 264209,Shandong,China;

2．College of Mechanical Science and Engineering,Jilin University,Changchun 130025,Jilin,China)

Abstract:Aiming at the steering stability of four-wheel-steering/driving vehicles,an sliding mode variable structure control algorithm is proposed based on the direct yaw moment.First,the relationship between the steering angles of frontand rear wheels is calculated through the Ackermann steering model,and all these angles are also calculated according to the control target of a zero sideslip angle.Then,the sliding mode variable structure control algorithm with the yaw rate and the sideslip angle as the control targets is designed to control the steering angle and driving torque of each wheel.Finally,the stability of the proposed control algorithm is proved by means of the Lyapunov method,and the software Matlab/Simulink is used to analyze the proposed control algorithm. Simulation results show that the proposed control algorithm can maintain the sideslip angle and the yaw rate within ideal ranges,and thus the steering stability of vehicles is effectively improved.

Key words:four wheel steering;four wheel driving;steering stability;direct yaw moment;sliding mode variable structure

中图分类号：U 461

doi:10.3969/j.issn.1000-565X.2015.08.011

文章编号：1000-565X(2015)08-0069-06

作者简介：赵立军(1975-)，男，博士后，副教授，主要从事新能源汽车、特种车辆技术研究.E-mail： zhaolijun@hitwh.edu.cn

*基金项目：国家自然科学基金资助项目(51275126);威海市科技发展计划项目(2012DXGJ13)

收稿日期：2014-06-10

Foundation item: Supported by the National Natural Science Foundation of China(51275126)