存在基站误差的稳健时差定位算法

房嘉奇, 冯大政, 李　进

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)



存在基站误差的稳健时差定位算法

房嘉奇, 冯大政, 李进

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

摘要：针对存在基站误差的目标无源定位问题,提出了一种基于修正牛顿算法的时差定位技术。众所周知,牛顿法对初值要求较高,较差初值会导致迭代发散,而且基站位置误差也会导致牛顿算法Hessian矩阵维数扩大和目标函数的缓慢下降,使运算量变大。该算法利用最大似然方法确定目标函数,运用牛顿法对目标位置进行迭代求解,对于计算过程中可能出现的病态Hessian矩阵,引入正则化理论修正病态的Hessian矩阵,使保证迭代收敛,同时简化算法降低Hessian矩阵的维数并且加速目标函数的下降趋势,使目标位置解脱离局部最小值,算法能够稳健高效的运行。实验结果表明:相对于传统牛顿法,此算法在初始值的选取上具有稳健性,对误差选取较大的初始值,仍能够保证算法的收敛性,同时加速了收敛速度,降低了计算量;相对于现有闭合式定位方法,此算法在噪声较大时具有较好的定位精度。

关键词：时差定位; 基站误差; Hessian矩阵; 正则化算法; 克拉美罗界

0引言

对未知发射源的无源定位问题,由于其在导航、跟踪监视、移动通信、无线传感器网络等方面的广泛应用,一直都是信号处理领域的研究热点。目前常用的无源定位技术可以分为到达角度(angle-of-arrival, AOA)、到达时间(time-of-arrival, TOA)、到达时间差(time-difference-of-arrival, TDOA)、到达频差(frequency-difference-of-arrival, FDOA)等方法。对于目标辐射源来说,TDOA定位技术利用目标到2个基站的到达时差信息来确定一条以两基站为焦点的双曲线,通过多个基站之间的测量值确定多条双曲线,其交点即为目标位置,在二维空间至少需要3个基站,三维空间至少需要4个基站来确定目标的位置。相对于TOA技术需要知道目标发送信号的准确时间,以及目标的接收基站的时钟同步等要求,TDOA定位技术不需要建立目标与基站的合作关系,因而在现实中得到广泛的应用。

因为需要求解的时差等式是非线性的,目标的定位问题并不是一个简单问题。最大似然(maximum likelihood, ML)估计能够对非线性问题能够提供渐进无偏解,但它需要进行格点搜索,计算量很大,在实际应用中难以实现。泰勒展开式(Taylor-series, TS)方法通过将时差频差非线性等式线性化[1]来求解该问题,但它需要具备一个良好的,接近目标实际位置的初值来保证迭代收敛。近年来,许多闭合式算法被提出用来解决TDOA定位问题[2-13],其中广泛应用的二次加权最小二乘(two-step weighted least squares， WLS)算法[2-5]引入关于目标位置的附加参数,采用WLS算法给出了定位方程组的非迭代解析解,该方法在噪声较小的时候具有较高的定位精度。一些学者通过引入半定规划(semi-definite programming, SDP)技术[12-13]利用凸优化方法对目标初始位置进行求解,然后通过迭代确定目标位置,该方法计算量较大,如果初始值不够精确,目标位置可能陷入局部最小解中。上述算法均假设接收基站位置精确已知,但在实际应用中,即使通过全球定位系统所获得的基站位置与真实位置之间也存在着误差。然而,TDOA定位问题的非线性特征又使目标定位精度对基站的位置精度非常敏感,基站位置微小的偏差可能导致目标定位精度较大的损失。在此基础上,一个扩展的WLS[14-16]算法被提出用于求解存在基站误差情况下的目标定位问题,该算法在小噪声下能够对目标进行精确定位。

闭合式方法的本质思想是将非线性问题线性化,但线性化非线性问题必然会带来性能的损失,因此闭合式方法都会面临所谓的“门槛效应”,当噪声功率超过一定值时, 通过闭合式算法得到的目标位置精度变差,将目标位置作为初值再通过迭代方法求解时,又会因为较差的初值导致迭代发散;如果考虑基站位置误差,迭代算法又会由于高维度Hessian矩阵和慢速下降的目标函数而使计算量变得很大。本文提出了修正牛顿算法,解决了牛顿算法的初值问题以及由基站误差引起的计算复杂性问题。首先利用最大似然估计确定目标函数,运用牛顿法作为优化方法对目标位置进行迭代求解,对于计算过程中可能出现的病态Hessian矩阵,运用正则化理论构修正病态的Hessian矩阵,从而保证算法的迭代收敛性。对于基站误差造成的高维度Hessian矩阵和慢速下降的目标函数,首先假设基站平台不存在误差,在此情况下先对目标位置进行求解,然后再考虑基站位置误差,对平台及基站误差进行联解精确估计。上述的简化步骤能够降低Hessian矩阵维数,加快收敛速度,使求解的目标位置脱离局部最小值,从而使本文算法变得可行高效。

1系统模型

(1)

不考虑非视距传播的影响,为计算方便以第1个接收基站为中心基站,根据多个TDOA测量值可建立方程组

(2)

d=Gr+n

(3)

(4)

式中，Qt,Qs为TDOA测量噪声与基站位置误差噪声的协方差矩阵E(nnT)=Qt,E(ΔsΔsT)=Qs。

2本文方法

牛顿法是一种需要初始估计值的迭代算法,在每一次迭代中通过求解目标函数的局部最小二乘解来改进估计值,直到搜索到正确解上。每次迭代的改变量

(5)

更新的迭代点x(k+1)可表示为

(6)

(7)

(8)

式中

(9)

(10)

(11)

(12)

(13)

(14)

由式(5)和式(6)可得

(15)

可以看到,求得的θ不仅包括了目标的位置信息,还包含了基站的位置信息,θ中的前3个元素即为所求的目标位置。通过式(8)可以看出,在考虑基站误差时,矩阵维度变为3+3M的方阵,其矩阵求逆运算量较大,而且受基站误差影响,目标函数的下降趋势会变得非常缓慢。本文算法提出了一种改进方法,首先假设基站位置不存在误差,在此情况下对目标位置进行求解,将求解目标位置作为初值,再考虑基站位置误差,对目标及基站位置进行联解精确估计。上述步骤能够使目标位置解脱离局部最小值,从而加快了收敛速度,降低Hessian矩阵维数,实验结果验证了本文算法的有效可行性。当不考虑基站误差时,目标函数可退化为

(16)

(17)

(18)

(19)

式中，U为单位正交矩阵UTU=In；Σ=diag(σ1,…,σn);σi和向量ui为特征值和与其相对应的特征向量,由式(5)我们得到迭代的改变量为

(20)

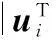
(21)

经过修正后的修正量为

(22)

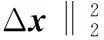
3算法步骤与计算复杂度分析

在实际中我们并不知道目标的真实位置,因此随机选取迭代的初值是不合理的,通常迭代算法的初始值都是通过闭合式算法求得,因此本文通过在闭合式算法中广泛应用的two-stepWLS算法来获得目标的初始位置。

本文算法步骤如下。

步骤 1给定初始值x(1),允许误差Δ=10-6,置k=1,l=1。

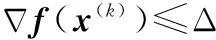
步骤 4置k:=k+1,转步骤2。

步骤 7置l:=l+1,转步骤5。

4仿真实验

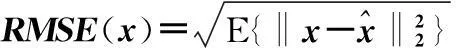
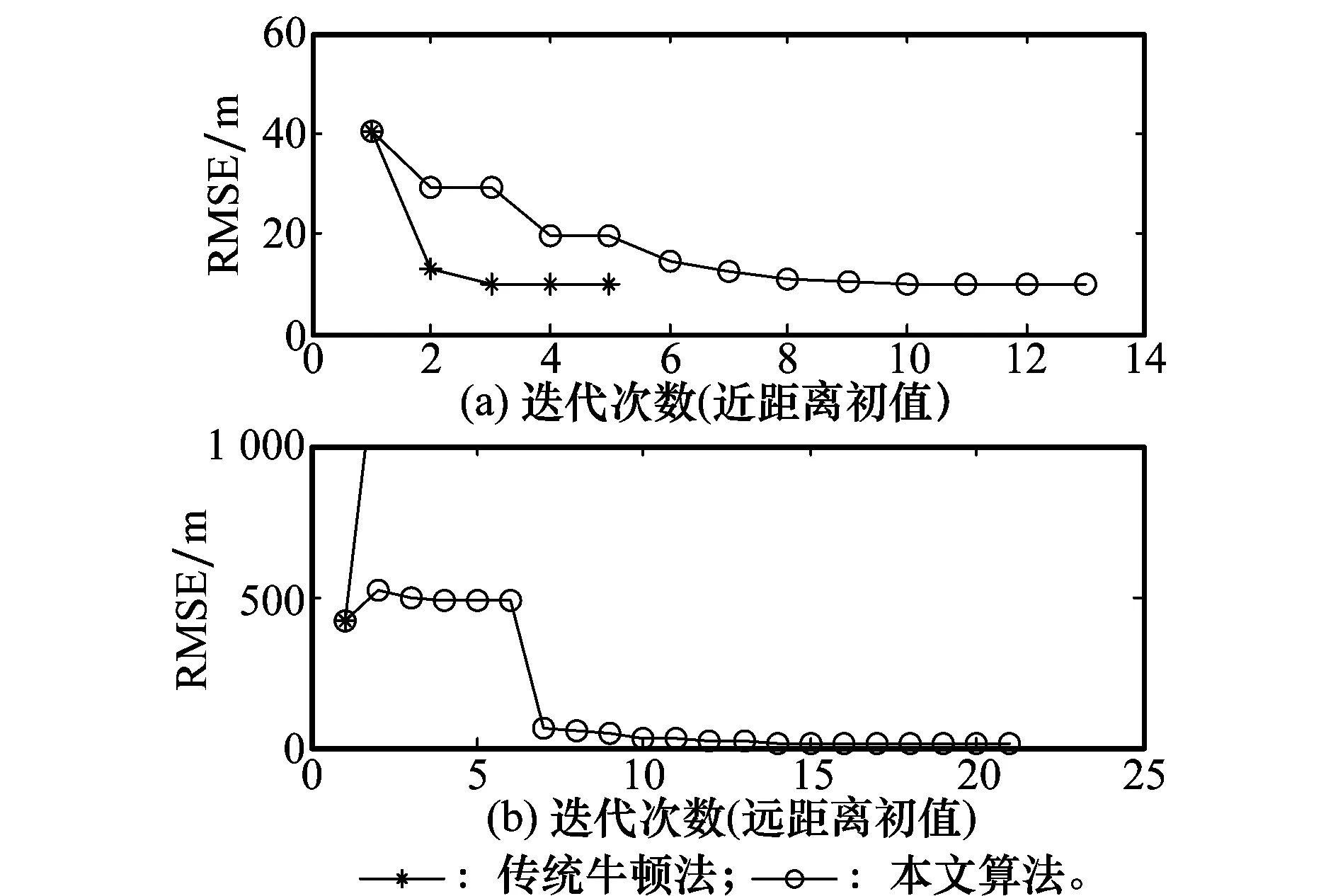
图1　目标位置为(280,325,275)时本文算法与传统牛顿法受初值影响比较

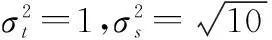
图2　目标位置为(2 800,3 250,2 750)时本文算法与传统牛顿法受初值影响比较　　　　　　图3　目标位置为(280,325,375)时本文算法与传统牛顿法收敛性能比较

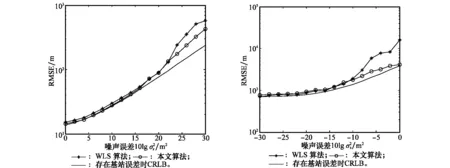
图4　目标位置为(280,325,275)时本文算法与WLS算法性能比较　　　　　图5　目标位置为(2 800,3 250,2 750)时本文算法与WLS算法性能比较

5结论

对于目标的无源时差定位问题,本文在牛顿法的基础上引入了正则化理论来修正由较差初值而带来的病态Hessian矩阵,在存在基站位置误差的情况下,通过2次牛顿法,减少了迭代次数,降低了运算量,高效而准确的求解目标的位置。通过分析和仿真结果表明,本文算法与传统牛顿法相比,在初始值误差较大的情况下仍能够对目标进行精确定位,算法具有较强的稳定性,同时加速了目标函数的下降速度,减少了计算量。与闭合式算法相比,在噪声较大的情况下本文算法能够对目标位置精度进行再次提高,定位误差更接近于CRLB下界,而且该算法收敛较快,计算量小,具有良好的实用价值。

参考文献：

[1] Kovavisaruch L, Ho K C. Modified Taylor-series method for source and receiver localization using TDOA measurements with erroneous receiver positions[C]∥Proc.oftheIEEEInternationalSymposiumonCircuitsandSystems, 2005:2295-2298.

[2] Ho K C, Xu W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J].IEEETrans.onSignalProcessing, 2004, 52(9):2453-2463.

[3] Ho K C. Bias reduction for an explicit solution of source localization using TDOA[J].IEEETrans.onSignalProcessing, 2012, 60(5):2101-2114.

[4] Wang Y, Ho K C. TDOA source localization in the presence of synchronization clock bias and sensor position errors[J].IEEETrans.onSignalProcessing, 2013, 61(18):4532-4544.

[5] Sun M, Yang L, Ho K C. Accurate sequential self-localization of sensor nodes in closed-form[J].IEEETrans.onSignalProcessing, 2012, 92(12):2940-2951.

[6] Wei H W, Peng R, Wan Q, et al. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J].IEEETrans.onSignalProcessing, 2010, 58(3):728-734.

[7] Huang J, Wan Q. Analysis of TDOA and TDOA/SS based geolocation techniques in a non-line-of-sight environment[J].JournalofCommunicationsandNetworks, 2012, 14(5):533-539.

[8] Hara S, Anzai D, Yabu T, et al. A perturbation analysis on the performance of TOA and TDOA localization in mixed LOS/NLOS environments[J].IEEETrans.onCommunications, 2013, 61(2):679-689.

[9] Lin L, So H C, Chan F K W, et al. A new constrained weighted least squares algorithm for TDOA-based localization[J].IEEETrans.onSignalProcessing, 2013, 93(11):2872-2878.

[10] Xu B, Sun G, Yu R, et al. High-accuracy TDOA-based localization without time synchronization[J].IEEETrans.onParallelandDistributedSystems, 2013, 24(8):1567-1576.

[11] Yu H, Huang G, Gao J, et al. An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J].IEEETrans.onWirelessCommunications, 2012, 11(1):44-47.

[12] Yang K, Wang G, Luo Z Q. Efficient convex relaxation methods for robust target localization by a sensor network using time differences of arrivals[J].IEEETrans.onSignalProcessing, 2009, 57(7):2775-2784.

[13] Wang G, Chen H. An importance sampling method for TDOA-based source localization[J].IEEETrans.onWirelessCommunications, 2011, 10(5):1560-1568.

[14] Ho K C, Lu X, Kovavisaruch L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors:analysis and solution[J].IEEETrans.onSignalProcessing, 2007, 55(2):684-696.

[15] Yang L, Ho K C. Alleviating sensor position error in source localization using calibration emitters at inaccurate locations[J].IEEETrans.onSignalProcessing, 2010, 58(1):67-83.

[16] Sun M, Ho K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J].IEEETrans.onSignalProcessing, 2011, 59(7):3434-3440.

[17] Hansen P C. Regularization tools:A matlab package for analysis and solution of discrete ill-posed problems[J].NumericalAlgorithms, 1994, 6(1):1-35.

[18] Hansen P C, Jensen T K, Rodriguez G. An adaptive pruning algorithm for the discrete L-curve criterion[J].JournalofComputationalandAppliedMathematics, 2007, 198(2):483-492.

房嘉奇(1984-),男,博士研究生,主要研究方向为无源定位与跟踪。

E-mail:fangjiaqi123@hotmail.com

冯大政(1959-),男,教授,博士研究生导师,研究方向为无源定位、雷达成像、阵列信号处理、盲信号处理、神经网络。

E-mail:dzfeng@xidian.edu.cn

李进(1985-),男,博士研究生,主要研究方向为盲信号处理。

E-mail:lijin342@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141031.0949.001.html

Robust source location algorithm using TDOA in the presence of

sensor position errors

FANG Jia-qi, FENG Da-zheng, LI Jin

(NationalLabofRadarSignalProcessing,XidianUniversity,Xi’an710071,China)

Abstract:For the source localization problem in the presence of sensor position errors, this paper presents a time-difference-of-arrival(TDOA)technique based on the modified Newton(MNT)algorithm. It is known that the NT algorithm suffers from the initialization problem. A bad initial may cause the iteration divergence. In addition, inaccurate sensor position condition also causes the NT algorithm computationally intensive due to the high-dimension matrix and the slow downtrend of the objective function. The new algorithm uses the maximum likelihood method to determine the objective function. For the problem of the ill-condition Hessian matrix caused by the bad initial, the algorithm introduces the regularization theory to modify the Hessian matrix, which ensures the iteration convergence. Meanwhile, the proposed algorithm reduces the degree of the high-dimension matrix and increases the downtrend of the objective function, and makes the solution escape from the local minimum value via a simplified iterative criterion. Experiment results show that compared with the classical Newton method, this new algorithm is robust to the initial value, and is still able to ensure its convergence even with an inaccurate initial value of large errors, it also speeds up the convergent rate and cuts the computation. Compared with some other closed-form source location methods, the new algorithm has better accuracy in large noise levels.

Keywords:time-difference-of-arrival(TDOA); sensor position errors; Hessian matrix; regularization method; Cramer-Rao low bound (CRLB)

作者简介：

中图分类号：TN 97

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.03

基金项目：国家自然科学基金(61271293) 资助课题

收稿日期：2014-06-04；修回日期：2014-09-30；网络优先出版日期：2014-10-31。