基于热核特征的SAR图像地物识别方法
王一丹, 林 伟, 延伟东, 温金环
(西北工业大学理学院, 陕西 西安 710129)
基于热核特征的SAR图像地物识别方法
王一丹, 林伟, 延伟东, 温金环
(西北工业大学理学院, 陕西西安 710129)
摘要:采用了一种空间敏感度特征包(spatially-sensitive bags of feature, SS-BOF)来实现合成孔径雷达(synthetic aperture radar,SAR)图像的地物识别。首先采用推广的核模糊C -均值方法分割SAR图像,提取SAR图像目标图形;采用Harris角点检测子提取角点,接着对目标图形进行Delaunay三角剖分;采用cotangent weight方法对三角剖分图赋值,进而求得离散化Laplace-Beltrami算子的特征值、特征向量,并计算SS-BOF,进而对地物目标进行识别,其识别方法采用比L1相似准则效果更好的相关系数法;最后与热核迹等热核不变量特征以及Hu不变矩特征进行对比。实验表明:空间敏感度热核特征的识别率高于热核不变量的识别率,并与经典的Hu不变矩特征比较,识别率有所提高。
关键词:地物识别; 合成孔径雷达图像; 热核不变量特征; 空间敏感度热核特征
0引言
合成孔径雷达(synthetic aperture radar,SAR)成像不受天气、光照等条件的限制,可对感兴趣的目标进行全天候、全天时的侦察,是目前重要的对地观测和军事侦察手段,其主要应用领域之一就是各种军事目标的检测和识别。随着SAR数据收集能力的不断增强, SAR地物识别已成为现代战场感知系统雷达信号处理的关键技术,日益成为国内外研究的热点。SAR图像的特征提取是地物识别的关键技术,基于SAR图像的地物识别的特征提取方法基本包括:目标峰值特征、阴影特征、目标小波低频特征等[1]。近期许多学者在此基础上进一步研究了SAR图像的特征提取与选择,以便更加精确的进行地物识别。例如,利用Zernike矩特征进行SAR图像的目标识别,取得了不错的效果[2];基于主元分析和稀疏表示的SAR图像目标识别,在没有预处理的情况下,提高了识别效率[3];基于G2DPCA的SAR目标特征提取与识别,G2DPCA在大大降低了特征维数的同时,又改善了识别性能[4],但有些方法需要依赖复杂的分类器,并且易受相干斑噪声的影响。
由于受超高频波的传播及其与场景间的相互作用,SAR图像呈现出大量斑点噪声,不像光学图像目标图形的边缘是连续的,易于处理。而且在获取SAR图像中,会受到气候、视角、时间等因素的影响,SAR图像会产生平移、旋转、尺度变化,甚至会产生形变,这给SAR图像识别工作带来极大困难。因此,寻找到一种优良稳定的特征对于SAR图像识别工作及其关键。
由于热核理论以热方程为基本变化,一直是解决场论问题的基本数学方法,并且在图像处理中已有相应的研究。主要因为热核表示穿过物体表面热能量的变化,可以充分的表示图像的几何特征且降低了矩阵的扰动性[5-7]。因此,本文首先研究了热核迹ζ′(0)等热核不变量特征对于几何形体的识别效果,经验证能够识别几何形体,但是对于经过仿射变换的图像识别效果不高,然后引入空间敏感度特征包(spatially-sensitive bags of feature, SS-BOF)。文献[11]研究此特征主要应用于非刚性变形的图像检索,本文则采用SS-BOF对经过仿射变换的SAR图像进行地物识别,并运用相似性度量方法将SS-BOF与热核不变量、Hu不变矩方法进行对比,其对比方法采用比L1相似准则效果更好的相关系数法。
1热核特征对几何形体的识别
对于一幅图形G,首先构造一结构G=(V,E,W),其中 V={1,…,N}是节点集(图G中所有的点的集合), E∈V×V是边缘集,W=(wij)N×N是相似矩阵,wij是节点与节点之间的边的连接权:

热核是热方程的本质,描述的是不同时间通过图边缘的信息流,信息流动的比率是由图的Laplacian矩阵决定的。图的热核可以用特征谱的指数计算[5],即
实质上,热核是一个|V|×|V|的矩阵,图G的节点u与v的关系式为
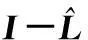
接下来将根据图的热核矩阵来计算热核不变量,包括:热核迹、Zeta函数、Zeta函数在零点处的导数ζ′(0)。
1.1热核不变量
1.1.1热核迹
(1)
从式(1)中看出,热核迹是图上热核矩阵的对角线元素之和,与特征值和时间尺度t有关,随着时间t的变化而变化。式(1)是通过图上所有点的热核合并而获得的热核迹[8]。与热核相似,热核迹包含了图的许多几何信息,除了具备谱特征的特性,又减少了矩阵扰动的影响、简化计算,还可以多尺度分析图结构的特点。理论上,由于图形的不同,其特征分解所得到的特征值不同,并与时间尺度同时刻画的图结构变化趋势也会不同。下面会在1.2节和1.3节具体研究热核迹对于不同几何形体的图结构的识别。
1.1.2Zeta函数和Zeta函数在零点处的导数
Zeta函数公式为
(2)
与Laplace矩阵的特征值和时间尺度s有关,并且Zeta函数与热核迹有很大的关系,为进一步说明它和热核迹的关系,本文引入梅林变换Zeta函数就可以写成[8]
换言之,Zeta函数与热核迹的梅林矩有关,即可以通过特征值和时间尺度s刻画图结构,它也是一种描述形状结构的方式。
对Zeta函数做进一步的分析,Zeta函数可以表示为
接着对其求导,并计算在零点处的值为
(3)
从理论上可以得出:不同形状的图形,所求得的ζ′(0)也会不同,特别是对于相似图形,其结果也会呈现一定比例。在接下来的实验中,本文将把ζ′(0)作为图特征,来研究是否可以区分不同的几何形体。
下面就通过热核不变量描述图像凹凸性以及相似几何形体,经实验发现,这几个特征可以反映目标的几何形体。具体过程如下。
1.2凹凸四边形
为研究的方便,取特殊的2个图形图1(a)和图1(b)。假设边长及每条边与X轴正方向的夹角已知,则可以计算出相似矩阵W,进而可以算得特征值与特征向量,利用前面的公式可以求得热核迹、Zeta函数、Zeta函数在零点处的导数,可以通过热核特征区分图像之间的差别,以及找出哪种特征区分最明显。

图1 凹凸四边形
下面就用热核迹、Zeta函数、Zeta函数在零点处的导数、描述2幅图形。
如图2所示,图2(a)随着时间的变化,2条曲线有明显的差别,图2(b)随着s的增大,2条曲线的差异也越来越大。总之,热核迹和Zeta函数描述凹凸性时,曲线有明显的差别,即可以反映几何形体的不同。

图2 凹凸四边形的热核迹与ζ函数曲线
当用Zeta函数描述的时候,分别给定s=1,2,3,4等整数时2条曲线差别也越大,如图3仅给出s=1,2的情形。当s值越大,所以当图形比较复杂的时候,就可以选取s值大一些,以便区分图形的不同。

图3 凹凸四边形的ζ(1)与ζ(2)曲线
1.3相似几何形体
如图4是3组相似的图形,即图形除了边权成一定比例外,其他都相同。
首先计算出拉普拉斯矩阵,并求其特征值与特征向量。从理论上求得的特征值、特征向量中可以得出,特征值与图形的大小是成等量反比,而每组特征向量是相同的。接下来就用热核不变量画出所对应图形的曲线,观察能否从画出的曲线中判断出原图形大致情况。
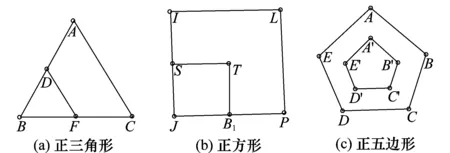
图4 相似几何形体
1.3.1用热核迹画出这3组曲线
如图5,不能从图形中直接得出每组几何形体都是成一定比例。但是可以通过热核迹判断出几何形体的形状。第1组三角形的热核迹都在3的附近,但不会超过3;第2组四边形的热核迹都在4的附近,但不会超过4;第3组五边形的热核迹都在5的附近,但不会超过5。
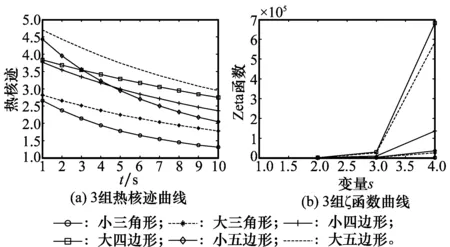
图5 相似几何体的热核迹与ζ函数曲线
因此,如果要辨别几何形体的不同,可以通过热核迹判断。
1.3.2用Zeta函数画出这3组曲线
从图5(b)看出,即s为变量时,能够区分相似几何形体的不同,但是不能从曲线中直接看出几何形体的关系。
当设定s=1,2时,图6的曲线都大致按一定比例分布。也即是从Zeta函数可以大致看出几何形体的相似。
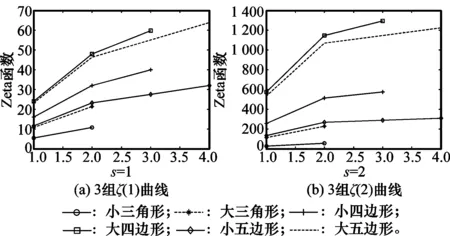
图6 相似几何体的ζ(1)与ζ(2)曲线
如图7,利用ζ′(0)所作的曲线和利用Zeta函数所作的曲线基本类似,可以大致描述图形的相似。综上,热核不变量特征可以用来识别几何形体,下面将继续探讨热核特征对于灰度图像的识别。
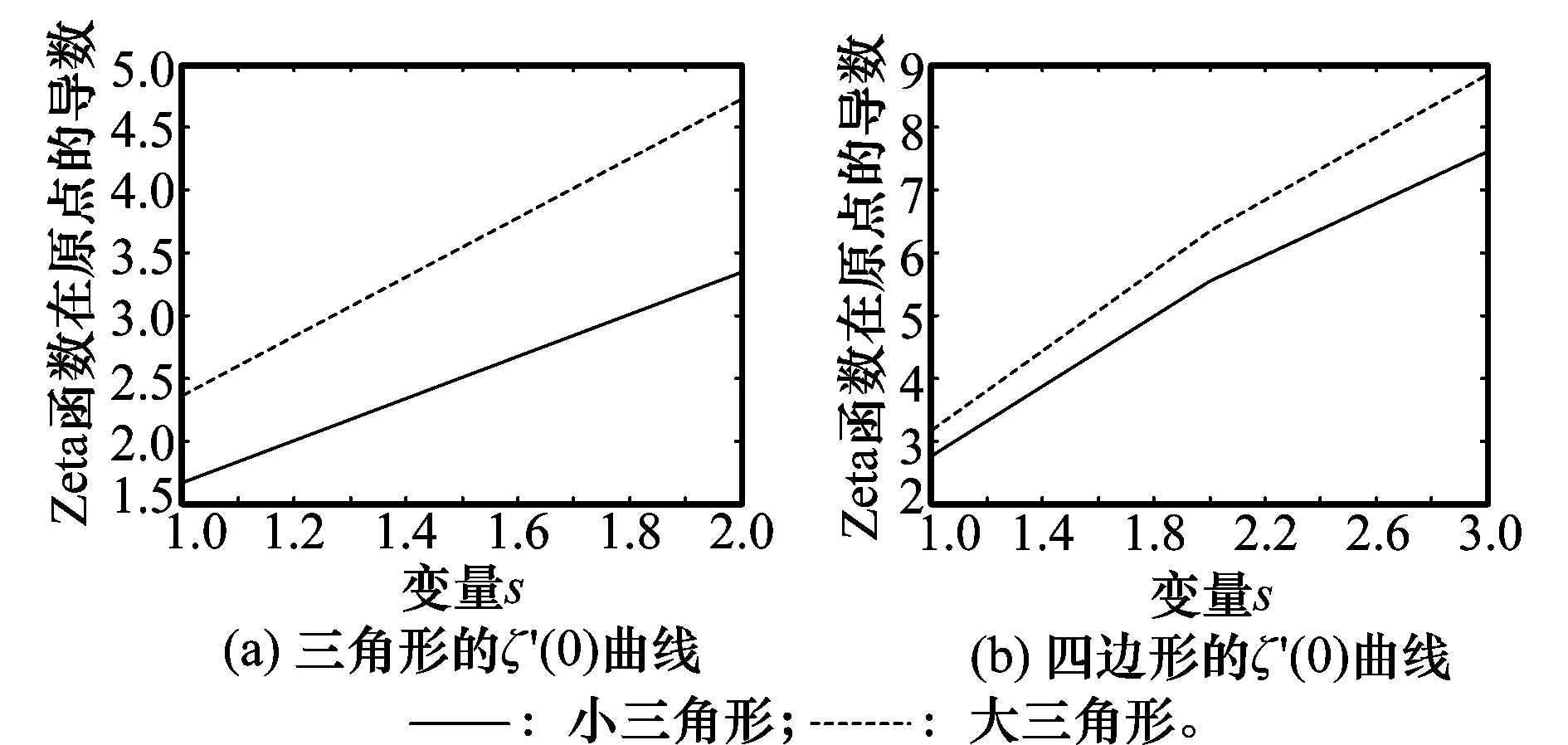
图7 相似几何体的ζ′(0)曲线
2热核特征对二值图像的识别
在研究SAR图像地物识别之前,首先把二值图像作为模拟图像进行实验,并在热核不变量的基础上,引入一种新的热核特征,验证这些特征是否可以用来识别二值图像以及它们的识别率。
2.1基于热核不变量的模拟图像的识别
针对二值图像目标的识别,首先需要提取关键点,而不是提取目标的每个像素点。以便简化计算,这里采用Harris角点检测子提取关键点。为了描述目标的结构特点,刻画点与点间的相关性,先对关键点进行Delauanay三角剖分,进而构造Laplace矩阵,求解离散化Laplace-Beltrami算子的特征值与特征向量,最后计算热核不变量,并验证热核不变量对二值图像目标的识别,流程图如图8所示。

图8 特征提取流程图
经实验发现:热核特征能够区分不同形状的二值图像。形状接近的目标图形,所对应的热核特征曲线也就更加接近,反之曲线越远离。具体步骤如下。
2.1.1提取目标图形的关键点及Delaunay三角剖分
研究灰度图像的识别,首先采用Harris角点检测子提取图像的关键点,由于每幅图像的结构不同,提取角点的个数也不相同。图9(a)和图9(b)经Harris角点检测子提取关键点,并对关键点进行Delaunay三角剖分,提取关键点如图10。

图9 二值图像
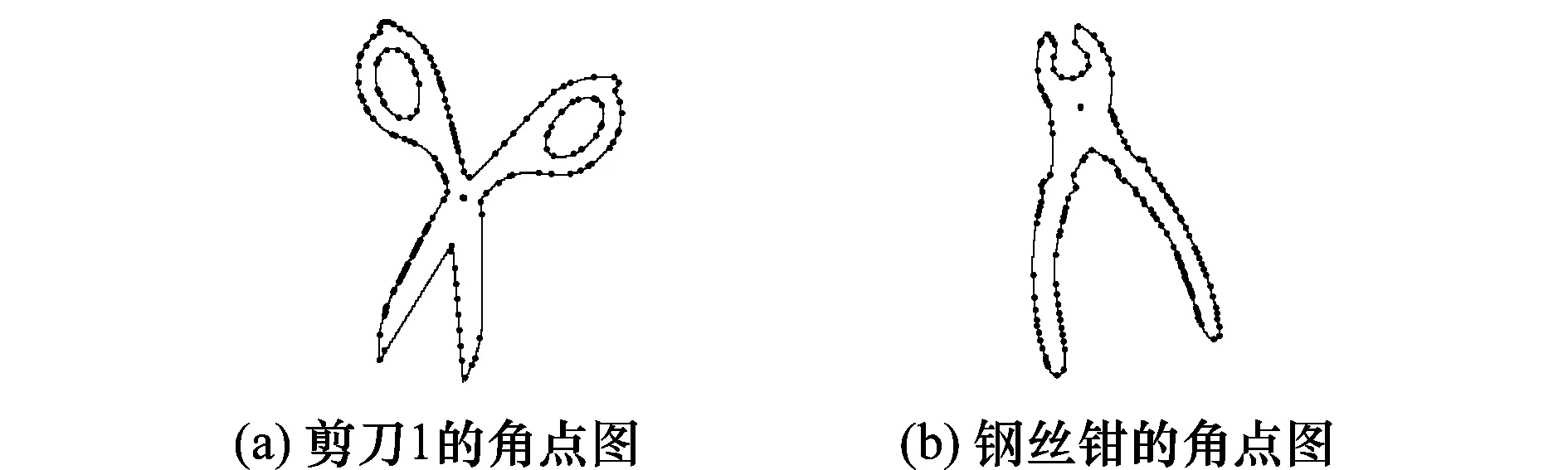
图10 角点提取图
图11是对图10图像的三角剖分。

图11 三角剖分图
2.1.2权的定义
在第1节中研究具体的几何形体,也就是边的长度,边与边的夹角都是已知的。当研究灰度图像时,由于提取的关键点不同,三角剖分的结构也有所不同,这样就应该找到合理的一个权矩阵的定义方法,进而离散化Laplace-Beltrami算子,最后计算热核不变量。在三角剖分网格上图像的离散化Laplace-Beltrami算子满足下面的等式:
(4)
离散化Laplace-Beltrami算子保留了连续的Laplace-Beltrami算子的许多性质,如半正定性、对称性和局部性。其中,ai为以xi为公共顶点的所有三角形区域面积:
2.1.3特征分解
式(1)可以写成如下形式:

特征值和特征向量的计算通过广义值分解为

式中,Λ为(k+1)×(k+1)的对角矩阵,对角元素为特征值λ0,…,λk;Φ为N×(k+1)的矩阵,Φ的列代表特征向量φ0,…,φk,即矩阵Φ中的元素φil代表顶点xi的第l维特征向量值。
2.1.4实验结果
利用式(1)计算图9中每幅图的热核迹,如图12所示,随时间尺度t的变化,曲线呈下降趋势,且从曲线的趋势可以区分出图9(c)和图9(d)2幅图像与其他5幅图像不属于同一类。
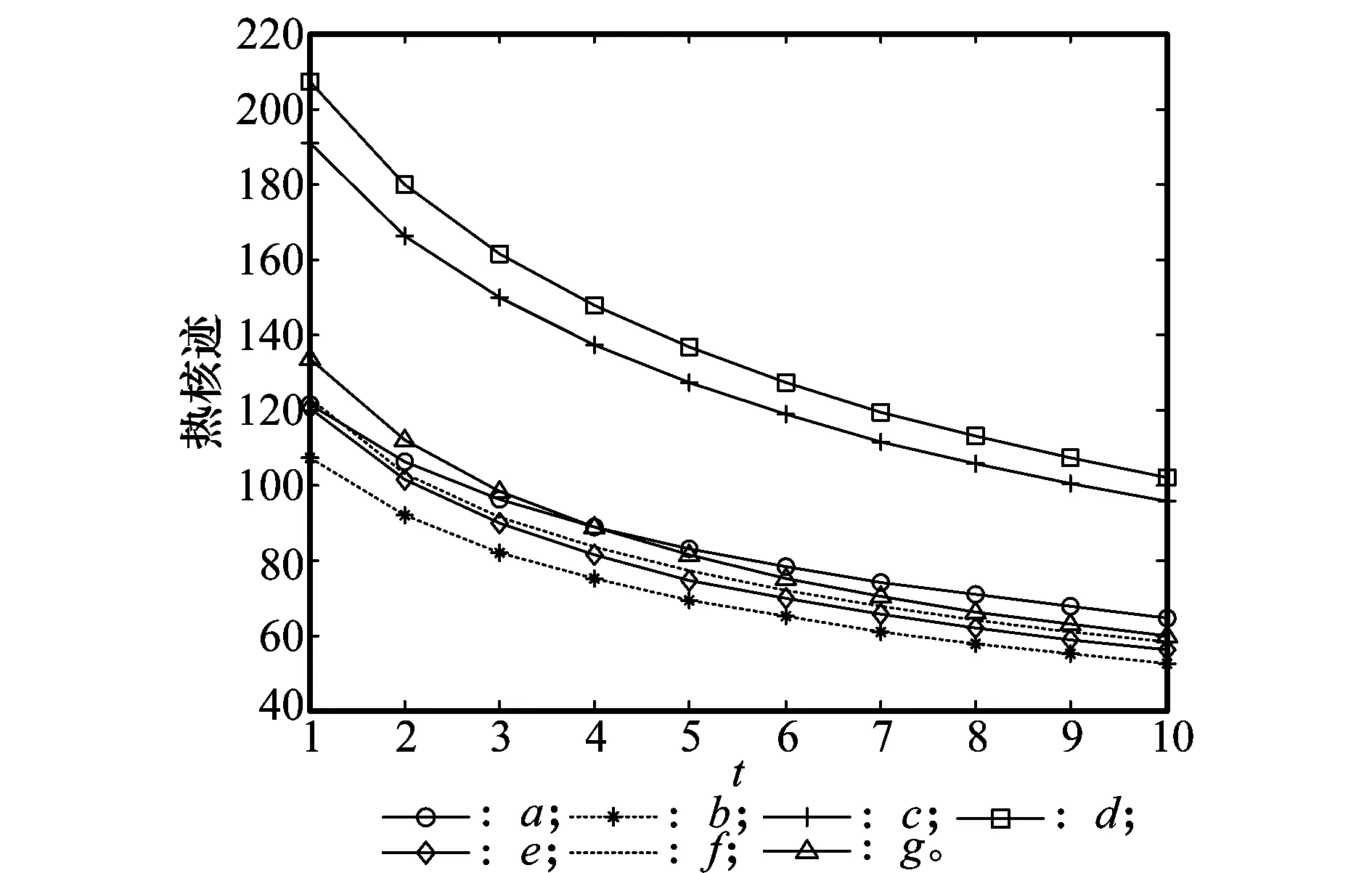
图12 热核迹曲线
接下来用热核不变量特征ζ′(0)描述上述7幅图像。如图13所示,随着特征值数的增加,越能体现目标局部结构的不同,从曲线的趋势,可以得出哪些图形可以归为一类。
综上,热核不变量不仅可以识别几何形体,还可以识别
二值图像。但是热核不变量对于经过仿射变换的图像识别率比较低(见表1)。因此引入一种热核特征:空间敏感度热核特征。经实验发现:此特征对于经过仿射变换的目标图形的识别率明显提高。
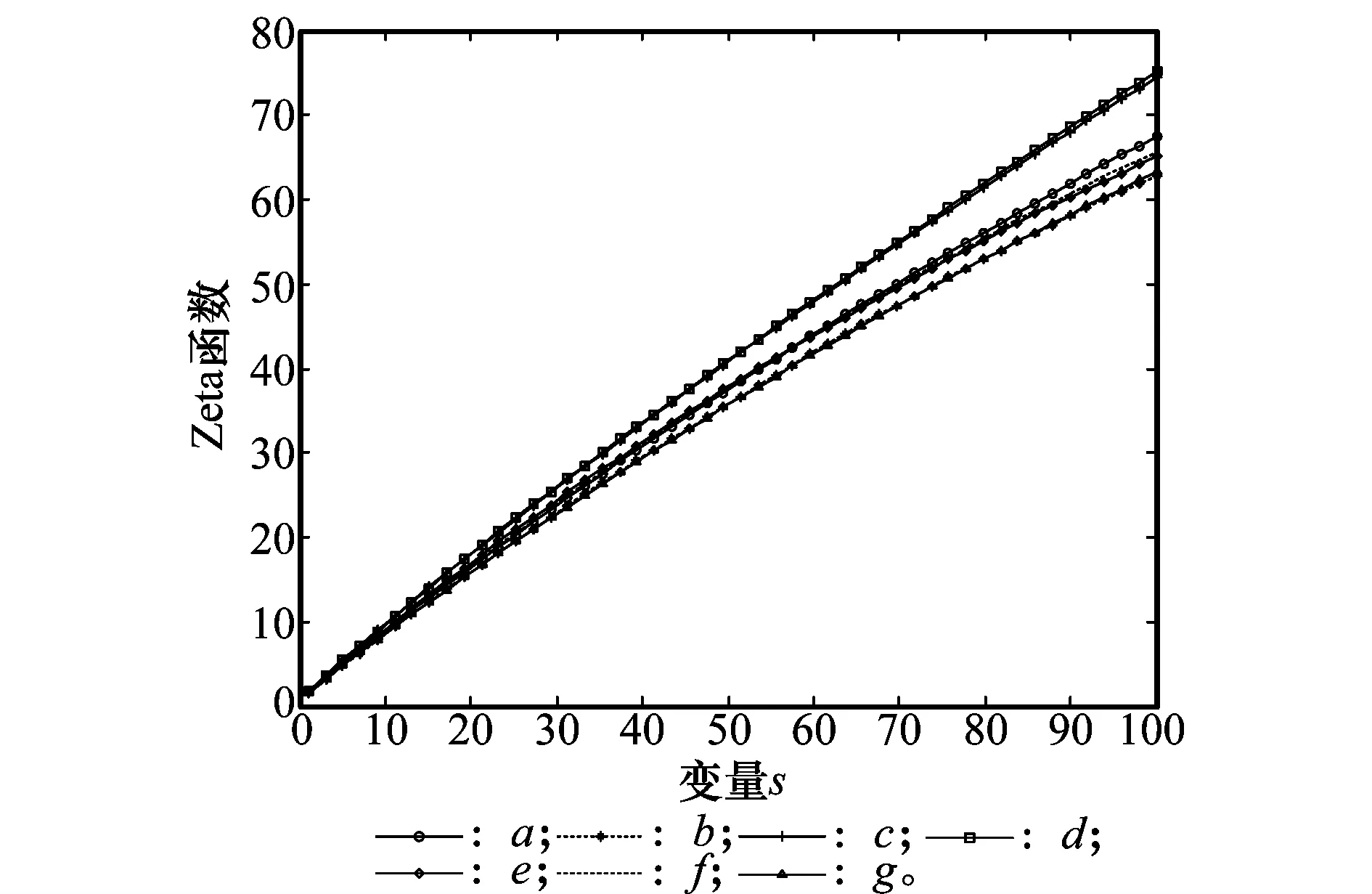
图13 ζ′(0)曲线

%
2.2空间敏感度特征包
热核特征Kt(x,y)有如下特征分解形式为
(5)
式中,λi,φi分别为Laplace-Beltrami算子的第i个特征值和特征向量[9]。这个热核特征(heat kernel signature,HKS)是由文献[10]提出的,具有稳健性和多尺度的特点,并且具有区分图形上不同点的特性。每个点的HKS都可以表示成一个向量,不同点间的HKS是对称的。对于一个图形X边缘上的每个点x,它的热核特征是个n维的向量P(x)=(p1(x),…,pn(x))T,每个元素表示如下:
式中,常数c(x)的选择需满足‖p(x)‖2=1。
特征分布:首先给定一个词汇Ρ={p1,p2,…,pN},表示描述符空间中的一组向量。那么对于每一个x∈X,定义这个特征分布θ(x)={θ1,…,θN}为1×N的特征向量,每一个元素定义为
式中,常数c(x)的选择需要满足‖θ(x)‖2=1。θi(x)可以解释为点x与词汇P中的算子pi之间的关联度。
对于整个图像X的集成特征分布产生了一个N×1的向量

称之为特征包。
从一维上升到二维的特征包,除了具有一维特征的优点,也避免了一维特征包只单纯的表示了每个点的特征,而忽略了图像任意2个点之间的联系,这里引入了SS-BOF[11]:
式中,F是一个N×N的矩阵,表示点x和点y相邻出现的频率,不仅充分体现了目标图形的点与点间的关联性,还通过积分的形式进一步刻画了目标的整体结构。在提取目标的特征之后,需要一种相似性准则来衡量特征的识别率。通过对比实验,采取比L1相似准则效果更佳的相关系数法来衡量特征的识别率。
式中,rij越接近1,越相似;越接近0,越疏远。
这里为便于相似性度量,可以将F返回一个N2维的列向量。
3实验结果与分析
在实验中,首先验证SS-BOF是否可以识别目标图形,其中取α=1.32,N=48.然后与热核不变量进行比较,最后与经典的Hu不变矩进行比较。实验表明:SS-BOF对于SAR图像的识别率高于热核不变量以及Hu不变矩[13]。
3.1基于SS-BOF的地物识别
首先选择图7所示的7幅图像,并按照流程图8所示的过程,提取空间敏感度热核特征SS-BOF,验证其是否可以识别二值图像。经实验表明,SS-BOF可以识别目标图形,实验结果如图14(a)所示,从曲线的趋势可以看出,曲线越接近,说明目标图形的图结构就越相似。
接下来验证SS-BOF对模拟图像的识别率。从图像库中选取30幅图像[14],并对图像进行平移,小角度的旋转与尺度变化,得到3 720幅图像,计算每幅图像的热核特征:SS-BOF、热核迹和ζ′(0),并计算Hu不变矩。用相关系数法进行相似性度量,结果如表1所示。

图14 SS-BOF曲线
结果显示,对灰度图像识别率最高的是SS-BOF,其次是Hu不变矩、ζ′(0)、热核迹。说明空间敏感度热核特征SS-BOF提高了对地物的识别率并优于Hu不变矩地物识别方法。以上是基于模拟图像的识别率的验证,实验证明SS-BOF特征确实有较好的稳健性,对经过仿射变换的图像有较好的识别率。
而本文研究热核特征的关键在于寻找对受相干斑噪声等影响的SAR图像地物识别的有效方法。下面将探究空间敏感度热核特征SS-BOF对SAR图像的识别率。
3.2基于SAR图像的地物识别
3.2.1基于水库的SAR图像识别
实验采用的数据是由RADARSAT-1卫星获取的2008年2月17日长江水库,丰收水库,白水河水库,沉抗水库,秦家碾水库和上游水库6幅原始模板图像,如图15所示。

图15 水库图像
针对SAR图像的地物识别,首先提取目标图形,本文采用推广的核核模糊C -均值方法[15-16]分割SAR图像,得到目标图形,然后按照如图8所示的步骤,计算每幅水库SAR图像的空间敏感度热核特征,并将其转换为一维向量图。
图14(b)表明空间敏感度热核特征不仅能够识别二值图像,同样能识别水库SAR图像。最后对6幅SAR图像平移,小角度旋转和尺度变换,共744幅。计算每幅图像的热核特征SS-BOF, 并计算热核迹和ζ′(0)以及Hu不变矩,用相关系数法识别,如表2所示。

表2 水库地物识别算法比较 %
3.2.2基于军用目标的SAR图像识别
本文使用的数据是MSTAR项目组公布的SAR地面静止军用目标数据,包括T72 (A64,A04),ZSU23/4,T62。图16是3类目标在俯视角为17o,不同方位角的SAR图像。对其进行平移,小角度旋转和尺度变换,共496幅。提取目标图形,按照图8的流程,计算SAR图像的热核特征,并计算Hu不变矩,最后用相关系数法识别结果如表3所示。

图16 军用目标图像

%
实验表明,热核不变量对SAR图像的识别效果不太理想,但是空间敏感度热核特征SS-BOF提高了对SAR图像的识别率,并且与经典的Hu 不变矩方法比较,体现了热核特征稳健性,识别率高于Hu不变矩方法。
4结论
由于热核不变量特征计算简便、矩阵扰动性小,可以识别几何形体,但是基于灰度图像和SAR图像的地物识别,效果不好。进而引入了空间敏感度热核特征SS-BOF,具有更好的稳健性。经实验发现,SS-BOF提高了易受相干斑噪声影响的SAR图像的识别率。对于非刚性的SAR图像的地物识别,是否可以用本文的思想进行处理,仍需做更深层次的研究。
参考文献:
[1] Zhang H, Wang C.HighresolutionSARimagetargetrecognition[M]. Beijing:Science Press, 2009.(张红,王超.高分辨率SAR图像目标识别[M].北京:科学出版社,2009.)
[2] Amoon M, Rezai-rad G. Automatic target recognition of synthetic aperture radar (SAR) images based on optimal selection of zernike moments features[J].IETComputerVision, 2013, 8(2):77-85.
[3] Liu Z J, Zhuang L K, Cao Y F, et al. Target recognition of SAR images using principal component analysis and sparse representation[J].SystemsEngineeringandElectronics, 2013, 35(2):282-286.(刘中杰,庄丽葵,曹云峰,等.基于主元分析和稀疏表示的SAR图像目标识别[J].系统工程与电子技术,2013,35(2):283-286.)
[4] Hu L P, Liu H W. SAR target feature extraction and recognition based on generalized 2DPCA[J].JournalofAstronautics, 2009,30(6):2323-2327.(胡利平,刘宏伟.基于G2DPCA的SAR目标特征提取与识别[J].宇航学报,2009,30(6):2323-2327.)
[5] Xiao B, Hancock E R, Wilson R C. Geometric characterization and clustering of graphs using heat kernel embeddings[J].ImageandVisionComputing, 2010, 28(6):1003-1021.
[6] Xiao B, Wilson R, Hancock E. Object recognition using graph spectral invariants[C]∥Proc.ofthe19thIEEEInternationalConferenceonPatternRecognition, 2008:1-4.
[7] Bronstein M M, Bronstein A M, Ovsjanikov M, et al. Shape recognition with spectral distances[J].IEEETrans.onPatternAnalysisandMachineIntelligence, 2011, 33(5):1065-1071.
[8] Mémoli F. Spectral gromov-wasserstein distances for shape matching[C]∥Proc.ofthe12thIEEEInternationalConferenceonComputerVisionWorkshops, 2009:256-263.
[9] Reuter M, Biasotti S, Giorgi D, et al. Discrete laplace-beltrami operators for shape analysis and segmentation[J].Computers&Graphics, 2009, 33(3):381-390.
[10]SunJ,OvsjanikovM,GuibasL.Aconciseandprovablyinformativemulti-scalesignaturebasedonheatdiffusion[C]∥Proc.of the Computer Graphics Forum,2009,28(5):1383-1392.
[11]BronsteinAM,BronsteinMM,GuibasLJ,etal.Shapegoogle:geometricwordsandexpressionsforinvariantshaperetrieval[J].ACM Trans. on Graphics, 2011, 30(1):1-7.
[12]JonesPW,MaggioniM,SchulR.ManifoldparametrizationsbyeigenfunctionsoftheLaplacianandheatkernels[J].Proceedings of the National Academy of Sciences, 2008, 105(6):1803-1808.
[13]YanF,MeiW,ChunqinZ.SARimagetargetrecognitionbasedonhuinvariantmomentsandSVM[C]∥Proc.of the 15th IEEE International Conference on Information Assurance and Security, 2009:585-588.
[14]BronsteinAM,BronsteinMM,BrucksteinAM,etal.Analysisoftwo-dimensionalnon-rigidshapes[J].International Journal of Computer Vision, 2008, 78(1):67-88.
[15]DongGH,XiZH,ZhaoYQ.C-Vlevelsetimagesegementationbasedonculturalalgorithm[J].Systems Engineering and Electronics,2012,34(7):1500-1504.(董光辉,席志红,赵彦青.基于文化算法的C-V水平集图像分割[J].系统工程与电子技术,2012,34(7):1500-1504.)
[16]FanM,TianZ,ZhaoW.UnifiedframeworkoftheFCM-typeclusteringalgorithmanditskernelversion[J].Electronic Design Engineering, 2013,4:134-136.(范明,田铮,赵伟.FCM型聚类算法的统一框架及其核推广[J].电子设计,2013,4:134-136.)
王一丹(1988-),女,硕士研究生,主要研究方向为遥感图像处理。
E-mail:wydlxy2012@163.com
林伟(1965-)女,副教授,博士,主要研究方向为统计建模与遥感图像处理。
E-mail:linwei@nwpu.edu.cn
延伟东(1979-),男,副教授,博士,主要研究方向为遥感图像处理。
E-mail:yanweidong@126.com
温金环(1974-),女,讲师,博士,主要研究方向为遥感图像处理。
E-mail:wjhgdsx@nwpu.edu.cn

网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141121.0931.004.html
Methods of SAR image terrain recognition based on heat kernel features
WANG Yi-dan, LIN Wei, YAN Wei-dong, WEN Jin-huan
(SchoolofScience,NorthwesternPolytechnicalUniversity,Xi’an710129,China)
Abstract:A spatially-sensitive bags of feature (SS-BOF) is introduced which is used for terrain recognition of synthetic aperture radar (SAR) images. Firstly,a generalized nuclear fuzzy C-Means method is used to segment the SAR images, then the target shape of each SAR image is extracted. Secondly, its corners are extracted by using Harris corner way, then the target graph is triangulated by Delaunay triangulation. Thirdly, the cotangent weight is assigned to the triangulation, then the eigenvalues and eigenvectors of the discretized Laplace-Beltrami operator and SS-BOF can be calculated, then objects are identified, and correlation coefficient means is adopted for the recognition method whose result is better than L1similar criterion. Finally, the SS-BOF can be contrasted with heat kernel trace and other heat kernel invariant features, also Hu invariant moments. Experimental results show that the recognition rate of spatially-sensitive heat kernel feature SS-BOF is higher than heat kernel invariant features, and compared with the classical Hu invariant moments, the recognition rate is increased.
Keywords:terrain recognition; synthetic aperture radar image; heat kernel invariant feature; spatially-sensitive heat kernel feature
作者简介:
中图分类号:TN 957
文献标志码:ADOI:10.3969/j.issn.1001-506X.2015.05.11
基金项目:国家自然科学基金(61201323, 61301196)资助课题
收稿日期:2014-05-04;修回日期:2014-09-27;网络优先出版日期:2014-11-21。

