具有饱和接触率的SIQRS模型的稳定性研究

张宏宇， 叶志勇

(重庆理工大学 数学与统计学院， 重庆 400054)



具有饱和接触率的SIQRS模型的稳定性研究

张宏宇， 叶志勇

(重庆理工大学 数学与统计学院， 重庆 400054)

首先建立一个具有饱和接触率的SIQRS模型，通过计算得到阈值R0的表达式；然后对阈值R0进行讨论；接着利用稳定性定理和Dulac定理得到无病平衡点和地方病平衡点的存在性和全局稳定性；最后通过计算机仿真验证了该结果的正确性。

SIQRS流行病模型； 阈值；饱和接触率

流行病的传播规律一直以来都受到人们的重视。近年来，一些新出现的流行病已严重威胁人类的生命健康，例如2014年发生在非洲地区的埃博拉疫情。有鉴于此，大量的数学模型被用于分析各种各样的传染病问题，并且已经取得大量的成果。在研究疾病的传播过程中，人们比较常用的是SI、SIS以及SIR模型等，这些模型一般考虑的是流行病传播的一般规律，而未考虑到疾病传播中个体差异。目前，对传染病的传染率为双线性传染率[1]或是标准传染率的传染病模型已经有了较深入的研究,但对具有饱和接触率[2-5]的模型研究还较少，而且根据传染病传播的实际情况，饱和接触率在实际传播过程中也是一种十分重要的传播特点。本文主要谈论了在具有饱和接触率的情况下SIQRS传染病模型地方病平衡点的全局稳定性。

1 模型的建立

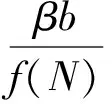
由此建立模型：

(1)

2 模型分析

对于模型(1),为了计算方便进行变换，令ω+δ+d1+p1=m和τ+d+p2=n，这样可以得到模型：

(2)

(3)

且可行域D是模型的正向不变集[7]。

模型的平衡点应满足下列方程：

(4)

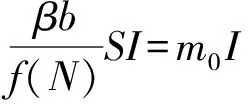
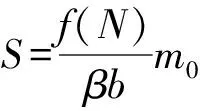
定理1 当R0<1时，无病平衡点E0是全局渐近稳定的。

证明 模型在E0处的雅可比矩阵[11-12]为

J0的特征方程为

由此可以得到特征值：λ1=-1,λ2=-c0,λ3=-(c0+α0),λ4=R0-1。所以，当R0<1时，λ1<0,λ2<0,λ3<0,λ4<0,E0是局部渐近稳定的；当R0>1时，可以得到当λ4>0,E0在可行域中是不稳定的。

下面证明 ：当R0<1，E0是全局渐近稳定的。

当t→+∞时，模型的极限方程为

(5)

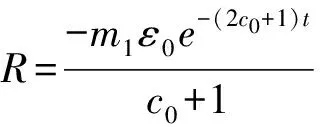
引理1 Hurwitz判据

考虑多项式方程：λn+θ1λn-1+θ2λn-2+…+θn-1λ+θn=0所有的根具有负实部的充要条件是：

其中k=1,2,…,n。当j>n时，补充定义aj=0。

定理2 当R0>1时，E*是全局渐近稳定的。

证明 模型在E*处的雅可比矩阵为

与J0等价。

根据Hurwitz判据得：

由此判据得到特征方程的4个特征根均具有负实部，则当R0<1时E*是局部渐近稳定的。下面证明E*是全局渐近稳定的。

故系统在可行域内无闭轨线。又因为E*是局部渐近稳定的，所以地方病平衡点E*是全局渐近稳定的。

3 数值模拟

首先对系统中的一些参数赋值,从而验证无病平衡点和地方病的全局稳定性。选取参数A0=0.1,c0=0.01,m0=0.2,δ0=0.2,ω0=0.1,τ0=0.25,α0=0.4,这样可以计算出R0=30>1。显然,此时系统存在一个地方病平衡点,且此平衡点是全局渐近稳定的。取初始值分别为S(0)=0.8,I(0)=0.5,Q(0)=0.7,R(0)=0.6;S(0)=0.7,I(0)=0.6,Q(0)=0.75,R(0)=0.6，应用Matlab软件进行数值模拟,可以得到如图1所示的结果。

从图1中很容易看出，感染者在疾病开始流行的时候数量有显著的增加，但是随着时间的推移，数量上趋于一个稳定的数值，也就是说疾病最终形成地方病，并且是全局渐近稳定的。

接着来看另外一种情况。在系统中取参数，A0=1,c0=0.4,m0=0.8,δ0=0.1,ω0=0.1,τ0=0.25,α0=0.3并计算出R0=0.75<1。此时系统存在一个无病平衡点E0是全局渐近稳定的，初始值分别取S(0)=0.8,I(0)=0.4,Q(0)=0.6,R(0)=0.5;S(0)=0.7,I(0)=0.5,Q(0)=0.65,R(0)=0.6，应用Matlab软件对系统进行数值模拟，得到结果如图2所示。

图1 R0>1时在不同的初始值下地方病平衡点的全局渐近稳定性

图2 R0<1时，在不同的初始值下无病平衡点的全局稳定性

从图2中可以看出，感染者随着时间的推移，最终将趋于灭亡。

4 结束语

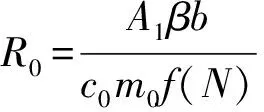
[1] 王拉娣.传染病动力学模型及控制策略研究[D].上海：上海大学,2005.

[2] 李桂花.传染病动力学模型性态分析[D].重庆：西南大学,2008.

[3] 邱爽.具有连续接种免疫的SEIS模型和具有饱和接触率的SEIV模型的动力学分析[D].昆明：昆明理工大学,2009.

[4] 陈军杰.几个具有隔离项的传染病模型的局部稳定性和全局稳定性[J].生物数学学报,2004(1):57-64.

[5] 陈立范,李维德,朱玑.具有饱和接触率的SIQR传染病模型的不同控制策略[J].兰州大学学报：自然科学版,2012(6):114-118.

[6] 马知恩.传染病动力学的数学建模与研究[M].北京：科学出版社,2004：1-20.

[7] 廖晓昕.论Lorenz混沌系统全局吸引集和正向不变集的新结果及对混沌控制与同步的应用[J].中国科学E辑:信息科学,2004(12):1404-1419.

[8] 马知恩,周义仓.常微分方程稳定性与稳定性方法[M].北京：科学出版社，2001.

[9] 王良成,李素斐.与Lipschitz条件相关的Hadamard型的新不等式[J].重庆理工大学学报:自然科学版,2011(1):120-123.

[10]岳超慧,张长勤,吴坚.非Lipschitz条件下C_h-空间中立型随机泛函微分方程解的存在惟一性[J].山东大学学报:理学版,2013(3):73-79.

[11]黄凯.雅可比矩阵乘法的证明[J].吉林省教育学院学报,2014,30(4):149-150.

[12]颜刚.流行病SIR模型的进一步研究[J].第一军医大学学报,2001,21(2):141-142.

[13]罗交晚,邹捷中,侯振挺.比较原理与Markov调制的随机时滞系统的稳定性[J].中国科学A辑:数学,2003(1):62-70.

[14]戎海武,徐伟,孟光,等.比较原理与随机时滞系统的稳定性[J].系统科学与数学,1999(2):230-235.

(责任编辑 刘 舸)

Analysis of SIQRS Epidemic Model with Saturated Contact Rate

ZHANG Hong-yu, YE Zhi-yong

(College of Mathematics and Statistics, Chongqing University of Technology,Chongqing 400054, China)

First, this paper constructed a SIQRS epidemic model with saturated contact rate. We got the thresholdR0bycalculating,inwhichthereexistsadisease-freeequilibriumpointandanendemicequilibriumpointbystabilitytheoremandDulacTheorem,atlast,thecomputernumericalvaluesimulationimpliesthattheconclusionisright.

SIQRSepidemic model; threshold; saturated contact rate

2014-10-15 基金项目：重庆市自然科学基金资助项目(2005BB8085)；重庆市教育委员会基金资助项目(KJ080622)

张宏宇(1990—)，男，河南信阳人，硕士研究生，主要从事微分方程与动力系统研究。

张宏宇， 叶志勇.具有饱和接触率的SIQRS模型的稳定性研究[J].重庆理工大学学报：自然科学版，2015(3):141-145.

format：ZHANG Hong-yu, YE Zhi-yong.Analysis of SIQRS Epidemic Model with Saturated Contact Rate[J].Journal of Chongqing University of Technology:Natural Science,2015(3):141-145.

10.3969/j.issn.1674-8425(z).2015.03.026

O175

A

1674-8425(2015)03-0141-05