手动变速器拨叉轴自锁槽的优化设计

陈颖宇，王光良，黄元毅，何耀华,韦 炜

(1.武汉理工大学 汽车工程学院,湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司 技术中心，广西 柳州 545000)



手动变速器拨叉轴自锁槽的优化设计

陈颖宇1，王光良2，黄元毅2，何耀华1,韦 炜2

(1.武汉理工大学 汽车工程学院,湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司 技术中心，广西 柳州 545000)

针对环簧式同步器退挡不平顺问题，分析了产生阻滞力的原因和影响因素。在保证足够的定位效果和进挡品质前提下，提出自锁槽渐变角度的设计方案，旨在减小退挡阻滞力，改善退挡平顺性。应用多目标参数优化方法，建立了自锁槽优化尺寸的数学模型，求得最优的尺寸组合。通过Adams动力学仿真模型和实车测试验证了该方案的可行性。

退挡力；同步器；自锁槽；渐变角度；优化设计

手动变速器由于成本低、驾驶娱乐性高，一直占据着很高的市场份额[1]，更好的换挡舒适性是变速器研发人员不断追求的目标。这与其变速操纵机构和同步器的结构类型相关[2]。虽然同步器对换挡力和平顺性影响很大，但由于成本的原因，采用简单更新高性能同步器的方法往往不是汽车生产企业的首选。而变速操纵机构的改进成本相对较低，基于操纵机构的结构优化来提升变速器换挡性能的方式更为企业所青睐。因此，寻求一个与同步器匹配的、低成本的操纵机构改进方案更具实际工程意义。

1 手动变速箱退挡不平顺的原因

退挡卡滞是手动变速箱常见的问题，具体表现为：对操纵杆施加一个较小的退挡力，操纵杆不能自动回位，必须辅之以持续作用力才能回到空挡。否则，由于互锁块的作用，驾驶员无法进行其他挡位的换挡操作。研究发现，通过操纵机构的精细化设计以匹配同步器的类型能解决这一问题，且改进成本低。笔者研究的变速器采用环簧式同步器，其结构如图1所示[3]。

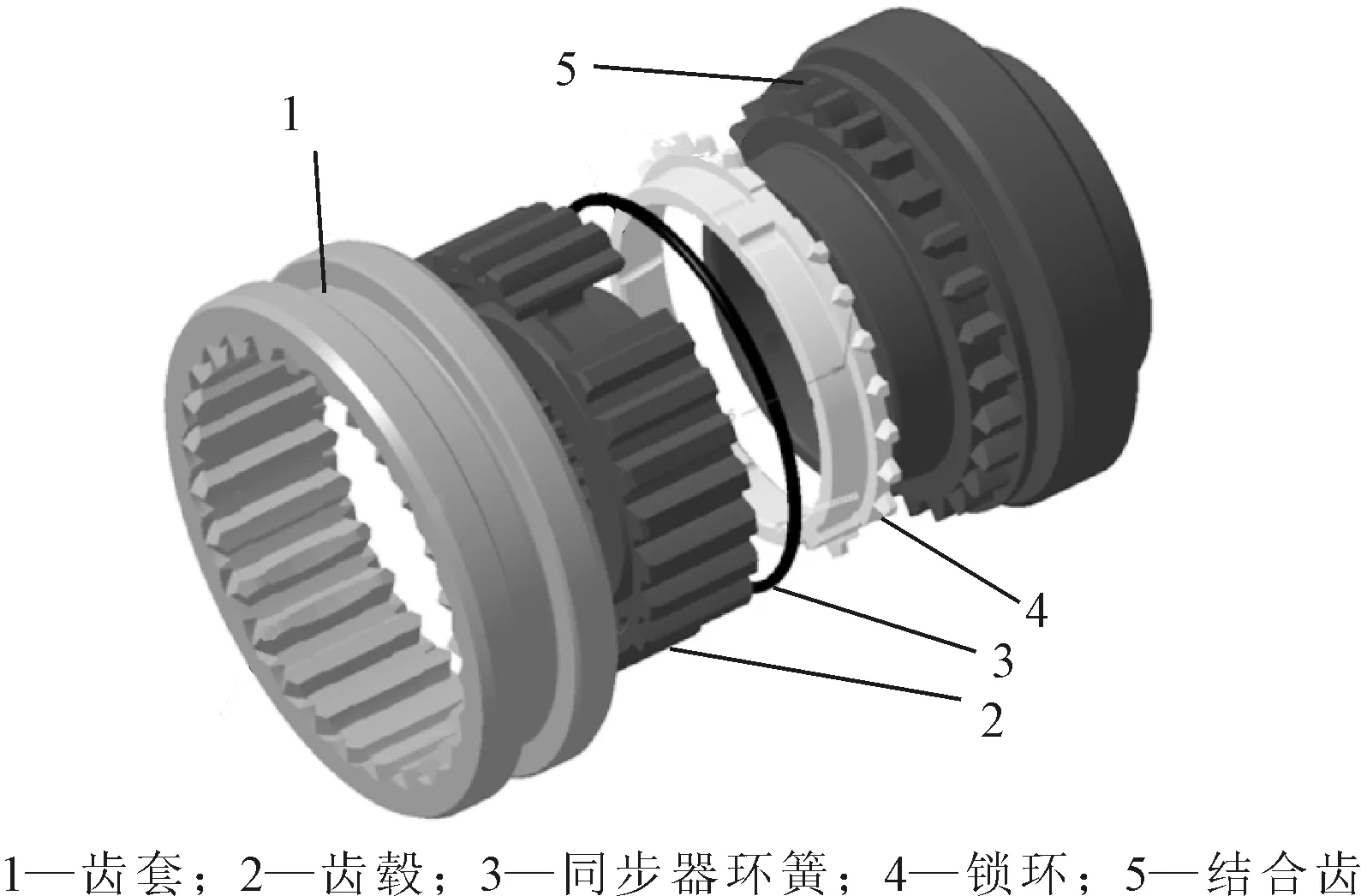
图1 环簧式同步器结构图

这种同步器由于零件数目少、成本低，在低价位微型车上得到了广泛应用，但存在换挡力偏大、换挡平顺性差等缺点。这是因为进挡时同步器环簧抵靠在锁环上，齿套的高齿起到推压同步器环簧和锁环直至与结合齿摩擦锥面紧紧贴合的作用，如图2(a)所示；退挡时，同步器环簧先随齿套移动，直至侧面抵靠在齿毂上，之后随齿套继续回位，环簧将对齿套的回位运动产生阻碍作用，形成退挡阻滞力,如图2(b)所示。

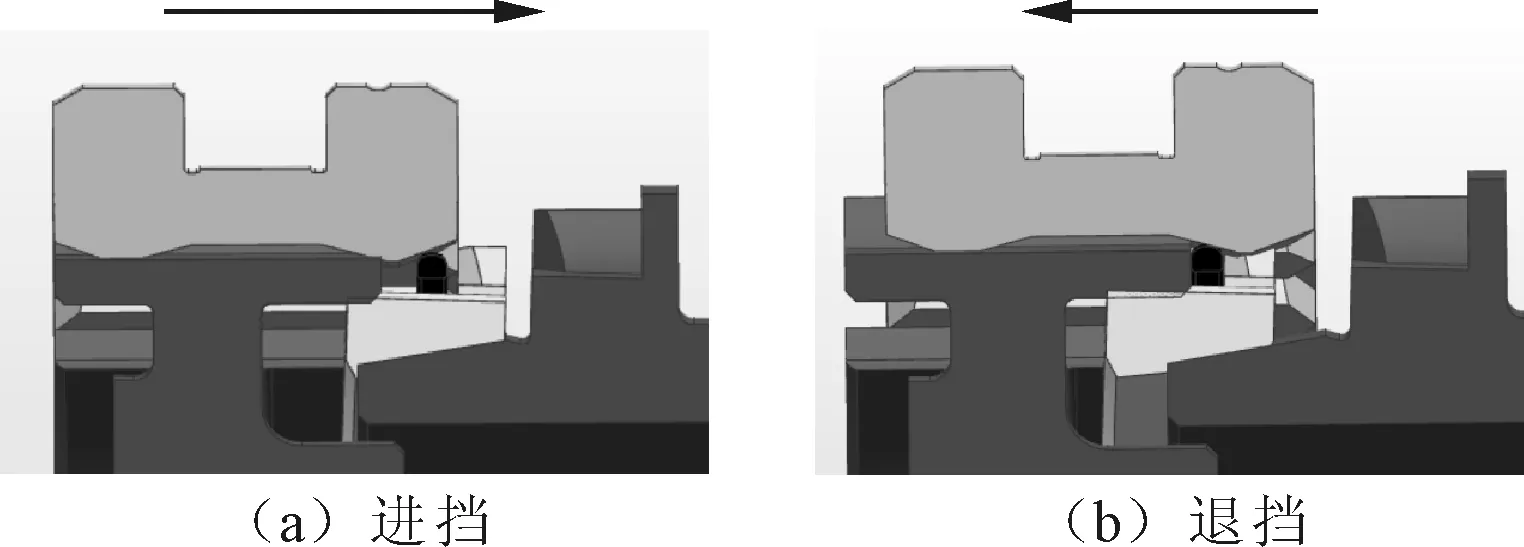
图2 进挡和退挡时同步器关键零件相对位置

为全面了解退挡阻滞力的大小及操纵杆运动至何位置时出现，利用英国里卡多公司的换挡性能测试系统GSQA(gear shift quality assessment system)对装有这种同步器的变速器进行装车测试，获得了退挡力与行程关系曲线，如图3所示。

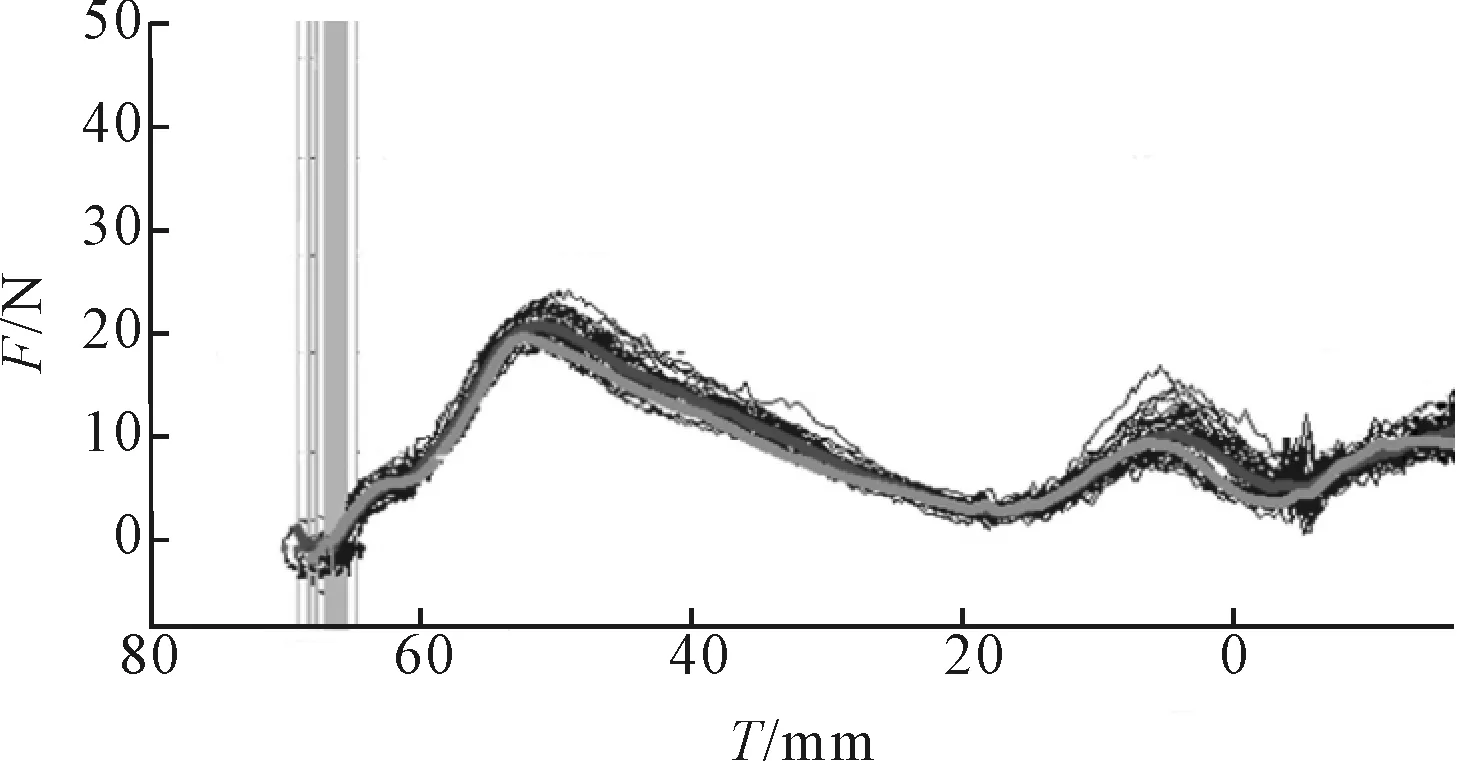
图3 1挡退挡力与行程关系曲线

由图3可见，退挡时，首先要克服一个20 N左右的退挡力，把操纵杆拨离挡位；其次，在距离空挡约10 mm的位置处还要克服一个约10 N的退挡阻滞力。当操纵杆运动到两个峰值力对应的行程之间时，驾驶员会产生已经换挡到位的错觉，从而试图换其他挡位，就会出现卡滞现象。

2 退挡阻滞力的影响因素

退挡阻滞力是由于同步器高齿内锥面在退挡时压缩同步器环簧产生的。在退挡过程中还有运动件间的摩擦阻力，包括拨叉轴移动时与箱体的摩擦、换挡摇臂旋转时与箱体的摩擦、变速箱与操纵杆间拉索芯线与套管的摩擦等[4]，如图4所示。

图4 手动变速箱换挡器运动机构示意图

系统的总摩擦力相对较小，且摩擦力会随着使用时间的延长而发生变化，通过减小摩擦力的方法解决该问题的可靠性较低。此外，自锁机构在即将退挡到空挡位置时，给拨叉轴力的方向与退挡力方向相同，即退挡快到位时，自锁机构再产生一个辅助退挡的作用力，如图5所示。

图5 自锁球与拨叉轴的自锁槽相对运动示意图

3 自锁槽的优化设计

3.1 优化设计的目标

首先确定最大退挡阻滞力对应的行程，然后依据该尺寸设计自锁槽的相关参数，最后验证改进的渐变自锁槽所能提供的辅助退挡力。上述实车测试获取的各挡位退挡阻滞力的最大值及距空挡距离的数据如表1所示。

表1 各挡退挡阻滞力最大值与相应的空挡距离

由表1可知，1、2挡阻滞力最大，3、4挡最小。这是因为1、2挡同步器尺寸最大，环簧直径最大，而3、4挡环簧直径最小，退挡阻滞力最小，均值约为6.35 N，实际操作中基本感觉不到退挡阻滞力。实践表明，若其他挡位的退挡阻滞力也能控制在7 N左右，退挡阻滞感即可大大削弱，甚至感觉不到阻滞作用。

以1、2挡为例，采用自锁槽角度的分段设计，充分利用自锁小球对拨叉轴的推力来减小退挡阻滞力，将阻滞力从11～12 N降到7 N左右。

退挡时高齿与同步器环簧的相对位置如图6所示。为了确定同步器退挡阻滞力出现的位置，首先计算得到高齿在距空挡3.83 mm处，环簧开始与高齿内锥面接触(图6(a))，齿套向空挡位置移动1.84 mm即达环簧压缩最大量(图6(b))，当齿套进一步移动进入第二个锥面时环簧即进入释放状态(图6(c))。

图6 退挡时高齿与同步器环簧的相对位置

理论上，距空挡约2.0 mm处阻滞力达到最大，按传动比转换至换挡操纵手柄上约为12 mm，考虑拉索的传动效率是0.9，约为10.8 mm。为使拨叉轴的尺寸设计更精确，应以同步器的退挡尺寸计算结果为依据。

自锁槽的结构还会影响空挡定位力和进挡感觉。合适的定位力应能使操纵杆稳定而准确地定在空挡位，给驾驶员清晰的空挡感觉；进挡感觉主要体现在离开空挡的过程中所需的换挡力与换挡杆行程的关系，直接影响换挡舒适性[5]。

目前拨叉轴上的自锁槽角度均采用单一角度，小的开口角度可以起到较好的空挡定位作用，但开始挂挡时较吃力，换挡手感差；大的开口角度使进挡平顺，但定位效果不佳。为解决这对矛盾，提出自锁槽渐变角度的设计方案改善空挡定位效果和进挡感觉，同时解决退挡不平顺问题。

3.2 主要设计参数的确定

3.2.1 自锁槽角度、自锁弹簧压缩量与换挡力三者关系

图7为拨叉轴、自锁球的受力分析图(以下分析均不考虑零件表面摩擦力)。

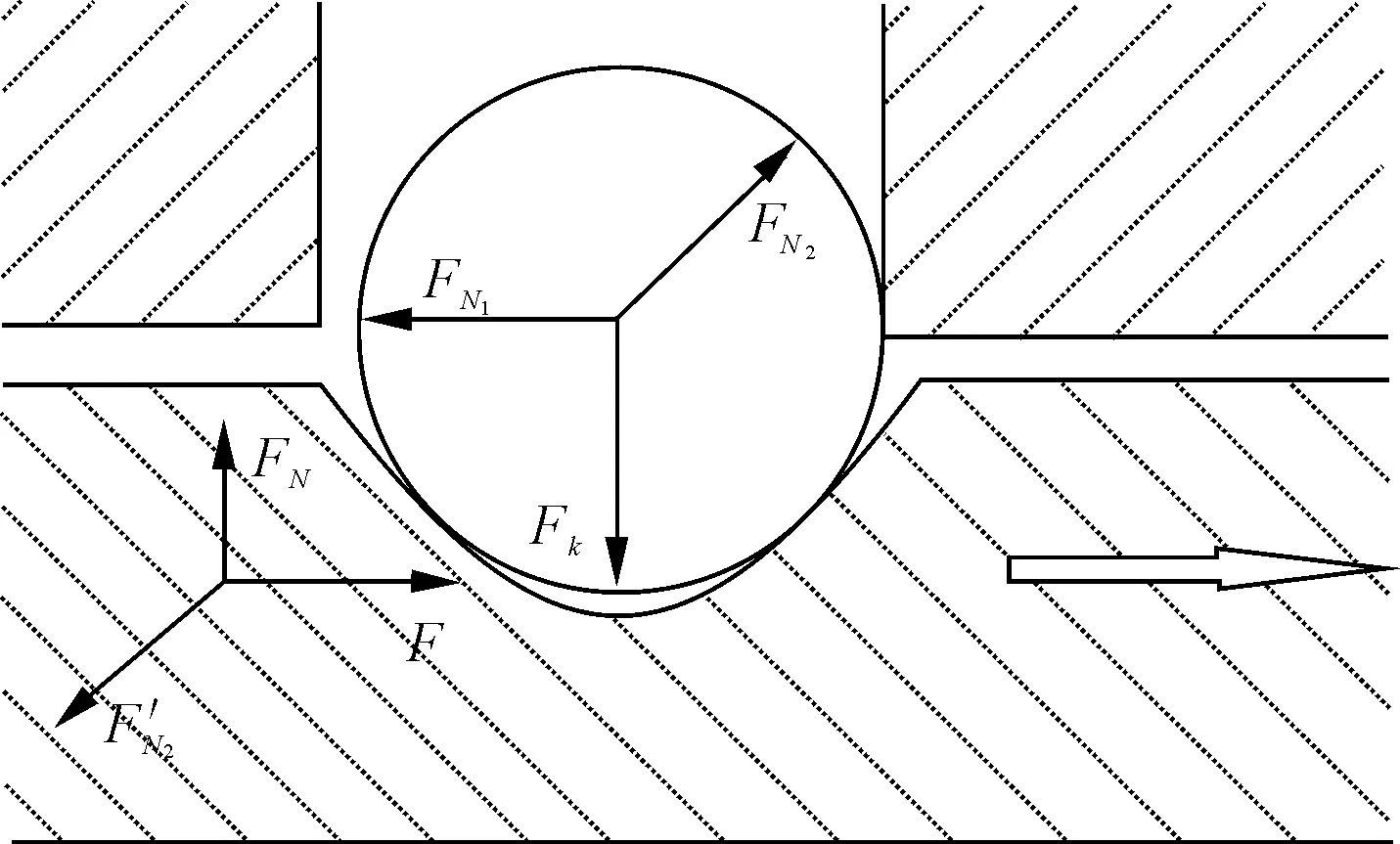
FN1—箱体对自锁球的支持力；FN2—拨叉轴对自锁球的支持力；Fk—弹簧对自锁球的压力；FN—箱体对拨叉轴的支持力；自锁球对拨叉轴的反作用力；F—轴向换挡力图7 拨叉轴与自锁球受力分析图

由图7可知：

F=Fkcotα=kΔxcotα

式中：Fk为自锁弹簧力；k=5.8 N/mm为弹簧刚度；α为1/2自锁槽开口角度；Δx为弹簧的压缩量。

换挡力F的大小由弹簧的压缩量Δx(反映小球沿自锁孔轴线的下落深度)和自锁槽开口角度2α决定。采用Matlab软件绘制1/2自锁槽角度α、弹簧的压缩量Δx与换挡力F三者的关系图，如图8所示。

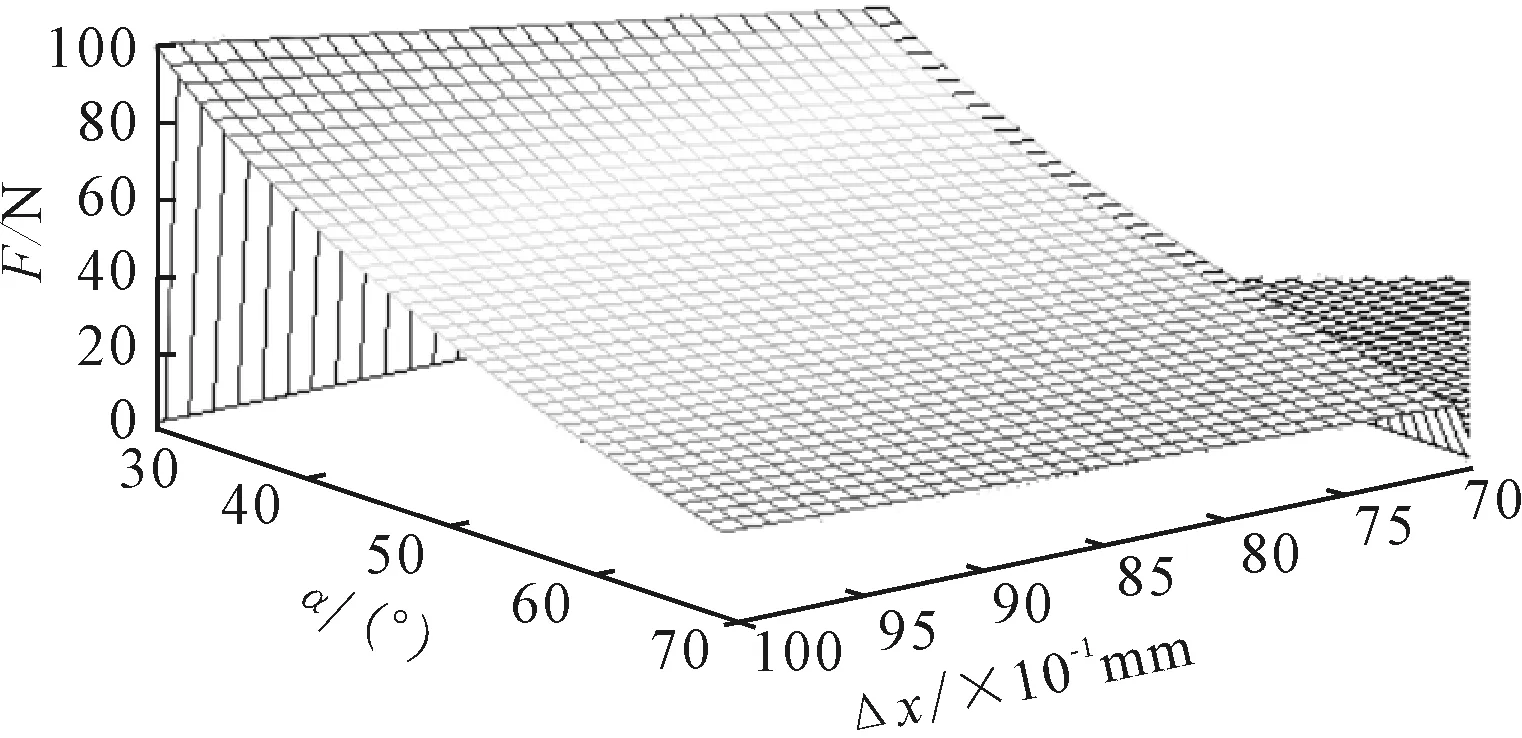
图8 自锁槽角度、自锁弹簧压缩量与换挡力三者关系图

3.2.2 多目标优化的数学模型

多目标优化问题是指超过一个优化目标并需要同时处理的优化问题，广泛应用于多个相互冲突和影响的子目标之间协调折中，使各目标尽可能达到最优化[6-7]。为了达到提高退挡平顺性，同时改善空挡定位效果和进挡感觉的3个优化目标，笔者采用多目标优化设计的方法改进拨叉轴空挡自锁槽的结构参数。

在实车测试时，用于评价空挡定位效果的操作为：以5 N以内的力晃动操纵杆时不会出空挡，自锁机构提供的空挡定位力应大于30 N，要使阻滞力达最大处具有很大的抵消作用，自锁槽应有较大的开口距离和较小的夹角；为了使进挡不吃力，自锁槽的夹角应较大；定位球的最大下落深度也不宜过大，否则定位球将无法从槽中爬出。

单一的拨叉轴自锁槽角度无法同时满足上述要求，对此根据优化目标在自锁槽的对应位置上设置相应的角度，进行分段设计。然而，自锁槽的轴向设计空间有限，如果设计两个以上的角度，每个角度可以起作用的行程将会很短，不仅效果不明显还给加工带来不便。因此，选择两个不同角度首尾相接的设计。

渐变槽的优化参数包括：角度θ1、角度θ2、开口距离Δ1，以及定位球落到槽底时球顶与拨叉轴母线的距离Δ2，如图9所示。

图9 渐变自锁槽的关键设计尺寸图

优化设计的参数用数学模型可表示为：

θ=(θ1,θ2);Δ=(Δ1,Δ2)

拨叉轴的退挡过程如图10所示。在距空挡距离为Δ1处，开始产生与退挡力同向的退挡辅助力，定位球绕槽边缘点O转动，小球的球心O1与O点连线和OO1自锁槽中心线夹角从0变化到90°-θ2，自锁小球与θ2角的槽面刚好相切，此时的弹簧压缩量在θ2斜面上达到最大，辅助力亦最大。再运动距离L后定位球完全落入槽中，辅助力从最大值逐渐减小为零,辅助作用消失。

图10 退挡时自锁小球与拨叉轴自锁槽的相对位置

自锁定位球对自锁槽辅助作用达到最大时，拨叉轴距空挡的距离为:

L=Δ1-rsinθ2

式中，r为自锁小球的半径，r=3.969 mm。

辅助力的数学模型可以表示为：

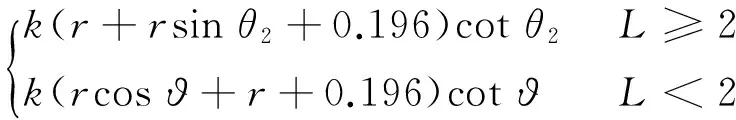
式中,ϑ为OO1与槽中心线间夹角，且sin ϑ=(Δ1-2)/r，ϑ∈(θ2,90°)。

设计参数θ和Δ的所有组合，并不都有意义。存在这样一种情况：若空挡时自锁定位球被θ2角槽面夹住，无法与θ1角槽面接触，则渐变槽的设计失去意义，如图11所示。为了保证每组解都是有效的，分析发现θ2、Δ1、Δ2应满足如下关系：

图11 无效组合示意图

综上所述，拨叉轴自锁槽结构参数组合优化数学模型表达式如下：

式中:Δ1∈(0,4.6];Δ2∈(3.969,7.938];θ1,θ2∈(40°,90°);g(θ1,Δ2)=kΔxcotθ1为空挡定位力;Δx=Δ2+0.196。

利用Matlab软件求解上述多目标优化模型，计算结果表明：当L≥2.0 mm时无解；当L<2.0 mm时存在非劣最优解，最终得到的渐变槽尺寸如表2所示。

表2 渐变式自锁槽关键设计参数

4 方案验证

4.1 Adams 动力学模型仿真验证

利用三维建模软件UG建立操纵机构模型，再以parasitoid格式导入动力学软件Adams中添加约束和驱动，有相对运动的零件之间添加接触力，接触力的参数设置如表3所示。最后设定仿真步长和时间并进行仿真[8]，仿真模型如图12所示。

表3 接触力关键参数设置

图12 Adams动力学仿真模型

仿真模型建立后，在换挡摇臂上施加驱动函数模拟换挡过程。3根拨叉轴分别采用原方案的130°和80°对比104°-84°的空挡自锁槽角度，仿真中不涉及同步器的运动，便于在同一仿真条件下进行对比，模型仿真结果如图13所示。

图13 3种拨叉轴自锁槽结构退挡力与行程关系曲线对比图

理论上，3种拨叉轴自锁槽的退挡轴向力初值均为：F=Fkcotα=5.8×7.262×cot 40°=50.196 N。由图13可知，104°-84°、80°和130°3种拨叉轴自锁槽的退挡轴向力初值分别为51.167N、51.156N、49.239N，误差均在2%以内。

对比图13中3条换挡力与行程曲线发现：在空挡定位效果和进挡操作感觉方面，80°的空挡定位槽表现为空挡定位力符合要求但进挡感觉不佳(进挡初始操作力偏大)；130°的空挡定位槽表现为进挡平顺但定位力不足。改进后104°-84°的渐变定位槽结构兼有满意的空挡定位力(定位效果明显)和良好的进挡平顺性。

在退挡平顺性方面，图13中标出了3种拨叉轴退挡时距空挡2mm处，自锁定位球对拨叉轴的推力。改进后的相应位置上产生53.28N的推力，相比于后两种单一角度产生的推力，分别增大了约28.48N和11.58N，将其换算至操纵手柄上可分别减小大约4.75N和2N的退挡阻滞力。表4列出了改进前后的退挡1、2挡阻滞力。

表4 改进前后的1、2挡退挡阻滞力

1、2挡拨叉轴的自锁槽角度改进后仅存在7.0 N的阻滞力，驾驶员几乎感觉不到阻滞作用，从而最大限度地改善了退挡平顺性。

4.2 实车试验

为验证方案的实际效果，将改进后的拨叉轴装箱后再利用英国里卡多公司的换挡性能测试系统进行测试，得到的换挡力与位移关系曲线如图14所示。

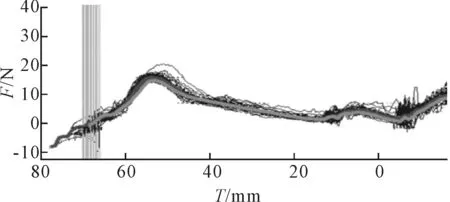
图14 改进后1挡退挡力与行程关系曲线

与图3相比，图14中1挡退挡至距空挡位置约10 mm处的退挡力减小了约3.8 N，使1挡退挡过程更平顺。考虑到实际操作的过程还受到操纵系统的摩擦力、驾驶员操作习惯等因素影响，试验数据与理论分析结果差异较小，进一步证实了拨叉轴渐变自锁槽设计方案的有效性和实用性。

5 结论

(1)拨叉轴自锁槽的角度、深度及开口距离直接影响换挡力的大小。自锁槽的角度越小，深度越大、开口距离越小，空挡定位力越大，但是进挡操作感觉不佳。

(2)相比于单一自锁槽角度，104°-80°的渐变角度设计既可保证足够的空挡定位力又使进挡操作更平顺，退挡阻滞力分别降低了41.3%和21%。

(3)同步器的工作原理和退挡运动过程是拨叉轴自锁槽优化设计的依据，同步器的运动与操纵机构的运动匹配是变速器整体换挡性能的重要影响因素。

[1] 徐海山.汽车用手动变速器发展趋势[J].现代零部件,2014(4)：31-36.

[2] 乐华.机械变速器换挡操纵机构的仿真与试验[D].上海：上海交通大学，2009.

[3] 柯建峰.微型车手动变速器换挡性能的优化[D]. 武汉：武汉理工大学，2014.

[4] 王欢.手动变速器操纵机构的仿真研究[D].武汉：武汉理工大学，2014.

[5] 崔传宝.机械式变速器换挡性能评价方法的初步研究[D].长春：吉林大学，2011.

[6] 徐玖平，李军.多目标决策的理论与方法[M].北京：清华大学出版社，2005：15-89.

[7] 马昌凤.最优化方法及其Matlab程序设计[M].北京：科学出版社，2010：174-218.

[8] BERNARD J E, CLOVER C L. Validation of computer simulations of vehicle dynamics[J]. SAE,2009040231.

CHEN Yingyu:Postgraduate; School of Automotive Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

Optimal Design on Manual Transmission Fork Shaft Self-locking Groove

CHENYingyu,WANGGuangliang,HUANGYuanyi,HEYaohua,WEIWei

The problem of retreat gears irregularity in ring spring synchronizer was discussed. The causes and influencing factors that generated blocking force were analyzed. Under the premise of ensuring adequate position effect and into-gear quality, a design on self-locking groove gradient angle was proposed to reduce the retreat gears blocking force and to improve the retreat gears smoothness. Multi-objective parameter optimization method was applied to establish the mathematical model. Then the optimized size of the self-locking groove was obtained. Finally, Adams dynamics simulation model and an actual vehicle test were used to verify the feasibility of the program.

retreat force; synchronizer; self-locking groove; gradient angle； optimal design

2015-04-07.

陈颖宇(1990-)，女，江苏常州人，武汉理工大学汽车工程学院硕士研究生.

校企合作科研基金资助项目(20132h0252).

2095-3852(2015)05-0562-05

A

U463

10.3963/j.issn.2095-3852.2015.05.008